MHMT 4 Momentum Heat Mass Transfer NavierStokes equations






























- Slides: 41

MHMT 4 Momentum Heat Mass Transfer Navier-Stokes equations Non-Newtonian fluids and Navier Stokes equations. Steady and transient flow between parallel plates, flow in pipe, annular gap, hydraulic diameter. Non. Newtonian fluids. RMW equation. Thixotropic fluids. Rudolf Žitný, Ústav procesní a zpracovatelské techniky ČVUT FS 2010

MHMT 4 Unknowns / Equations There are 10 unknowns (assuming isothermal flow): u, v, w, (3 velocities), p, xx, xy, …(6 components of symmetric stress tensor) And the same number of equations Continuity equation 3 Cauchy’s equations 6 Constitutive equations

MHMT 4 Navier Stokes equations Substituting the constitutive equation for viscous stresses (Generalised Newtonian Fluid) into the divergency term of the Cauchy’s equation gives, see the next slide…

MHMT 4 Navier Stokes equations Divergence of viscous stresses This is the same, but written in the index notation (you cannot make mistakes when calculating derivatives) These terms are small and will be replaced by a parameter sm These terms are ZERO for incompressible fluids

MHMT 4 Navier Stokes equations General form of Navier Stokes equations valid for compressible/incompressible Non-Newtonian (with the exception of viscoelastic or thixotropic) fluids Special case – Newtonian fluids with constant viscosity (compressible) This term is zero for incompressible liquids

MHMT 4 Navier Stokes equations Special cases 2 D flow (liquids) in Cartesian coordinate system 2 D flow in cylindrical coordinate system

MHMT 4 Navier Stokes equations Special cases 2 D compressible flow formulated in terms of stream function and vorticity reduces number of equations (continuity equation is automatically satisfied) and eliminates pressure. This term is zero for incompressible liquids These equations follow from the Navier Stokes equations using vorticity and stream function according to the previously introduced definitions

MHMT 4 Navier Stokes solutions The convective acceleration term makes Navier Stokes nonlinear and therefore analytical solutions can be found only when this term disappears (flow in straight pipes) or is very small comparing with the viscous term (Re<1, creeping flow). Modigliani

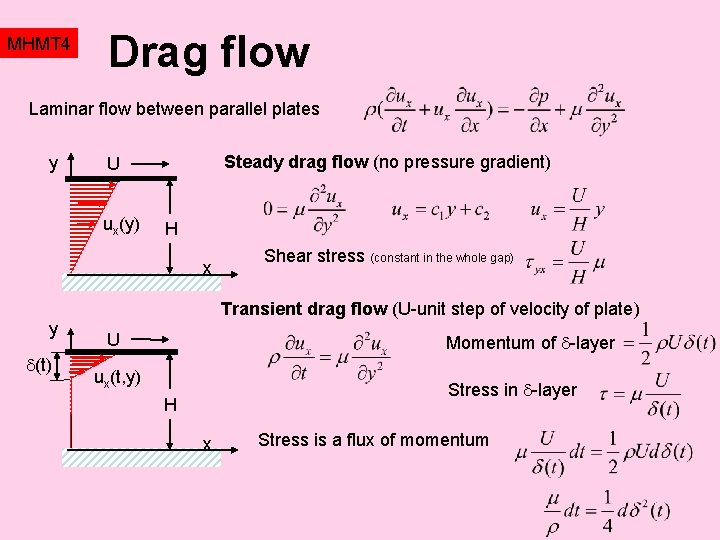
MHMT 4 Drag flow Laminar flow between parallel plates y Steady drag flow (no pressure gradient) U ux(y) H x y (t) Shear stress (constant in the whole gap) Transient drag flow (U-unit step of velocity of plate) U Momentum of -layer ux(t, y) Stress in -layer H x Stress is a flux of momentum

MHMT 4 Penetration depth Integration yields expression for thickness of the accelarated fluid layer (penetration depth) y (t) U ux(t, y) H x This solution is only an approximation, because the linear velocity profile with a turning point at is not an exact solution of the Navier Stokes equation. Exact solution exists in form of an infinite series for a finite thickness of gap H and for the case that H is defined by error function, giving more accurate prediction of the penetration depth

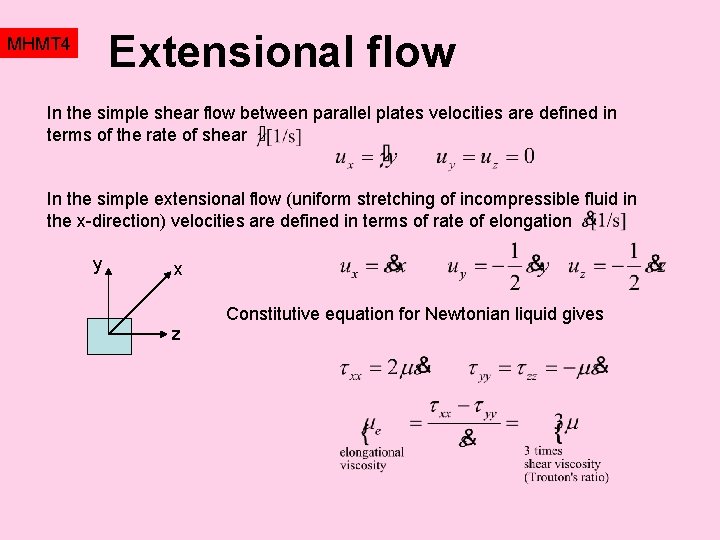
Extensional flow MHMT 4 In the simple shear flow between parallel plates velocities are defined in terms of the rate of shear In the simple extensional flow (uniform stretching of incompressible fluid in the x-direction) velocities are defined in terms of rate of elongation y x Constitutive equation for Newtonian liquid gives z

MHMT 4 Flow in a circular pipe Steady fully developed laminar flow – only one non-zero velocity component uz(r) Balance of forces for control volume (ring dr x dz) uz(r) dr r z D=2 R Constitutive equation (Newtonian liquid) dz Navier Stokes in z-direction General solution Boundary conditions r=0, R

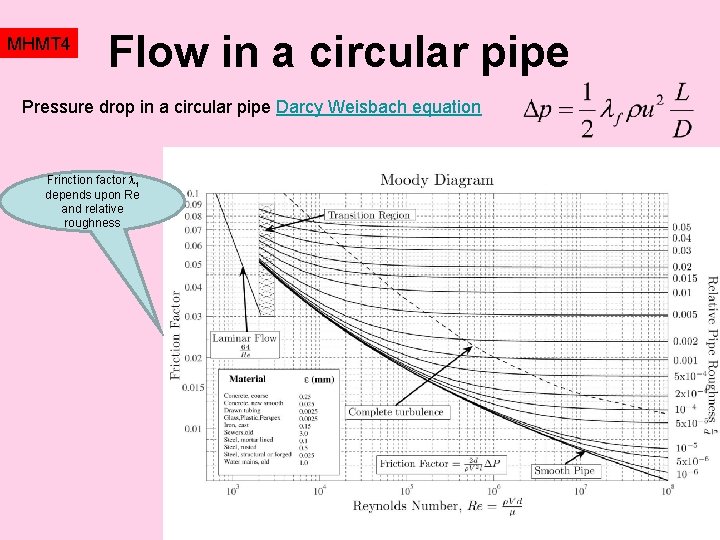
MHMT 4 Flow in a circular pipe Volumetric flowrate Hagen Poisseuille law Darcy Weisbach equation for calculation of pressure drop in channels Reynolds number is an indicator of laminar/turbulent flow regime. Above the value Re=2300 (in US) or 2100 (in EU ) the flow is mostly turbulent. The complete profile including the turbulent flow regime is presented in the Moody diagram (see next page) or described by using correlation Churchill S. W. : Friction factor equation spans all fluid-flow regimes. Chemical Engineering, 1977, 84 pp. 91 -92.

MHMT 4 Flow in a circular pipe Pressure drop in a circular pipe Darcy Weisbach equation Frinction factor f depends upon Re and relative roughness

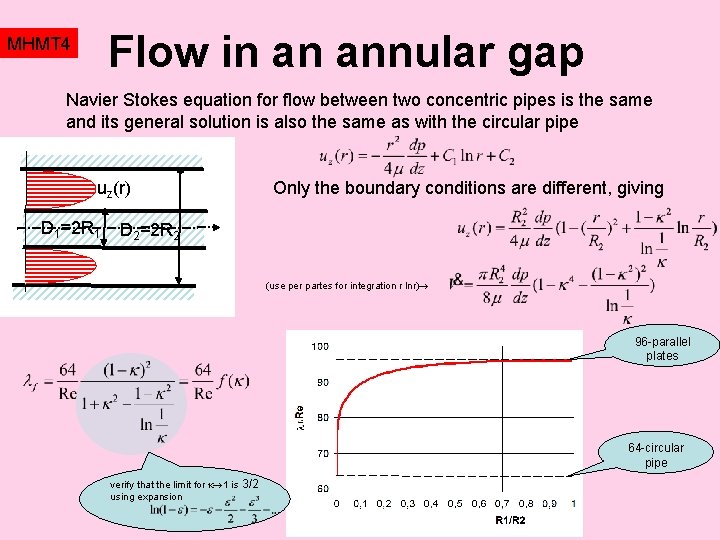
Flow in an annular gap MHMT 4 Navier Stokes equation for flow between two concentric pipes is the same and its general solution is also the same as with the circular pipe uz(r) D 1=2 R 1 Only the boundary conditions are different, giving z D 2=2 R 2 (use per partes for integration r lnr) 96 -parallel plates 64 -circular pipe verify that the limit for 1 is using expansion 3/2

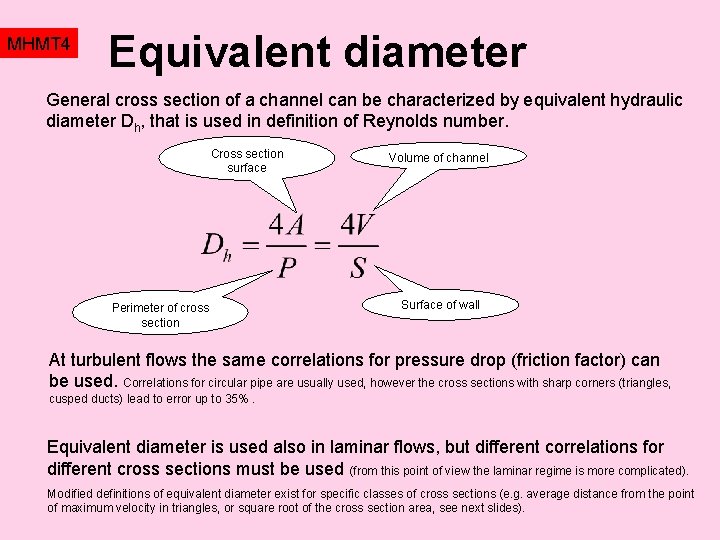
MHMT 4 Equivalent diameter General cross section of a channel can be characterized by equivalent hydraulic diameter Dh, that is used in definition of Reynolds number. Cross section surface Perimeter of cross section Volume of channel Surface of wall At turbulent flows the same correlations for pressure drop (friction factor) can be used. Correlations for circular pipe are usually used, however the cross sections with sharp corners (triangles, cusped ducts) lead to error up to 35%. Equivalent diameter is used also in laminar flows, but different correlations for different cross sections must be used (from this point of view the laminar regime is more complicated). Modified definitions of equivalent diameter exist for specific classes of cross sections (e. g. average distance from the point of maximum velocity in triangles, or square root of the cross section area, see next slides).

Equivalent diameter and f. Re MHMT 4 Equivalent diameter for rectangular cross section Increased f when compared with circular pipe b a Equivalent diameter for excentric inner tube is independent of excentricity! However f. Re decreases with the increasing excentricity! e f. Re varies from the values about 30 (corners) to about 130 (bundle of pipes)

MHMT 4 Non-Newtonian fluid flow

Non-Newtonian fluid flow MHMT 4 How to calculate the volumetric flowrate in a circular pipe as a function of pressure drop in the case of non-Newtonian fluids? In 1 D case (fully developed unidirectional axial flows) the constitutive equations for incompressible generalised Newtonian fluids (GNF) can be expressed as for Newtonian fluid shear rate shear stress for Power law fluid for Bingham fluid Volumetric flowrate for quite arbitrary radial velocity profile is

MHMT 4 Non-Newtonian fluid flow Radial shear stress profile follows from the equilibrium of forces w r (r) R This linear shear stress profile holds for any fluid and can be used for replacement of the integration variable r This is Rabinowitsch Mooney Weissenberg (RMW) equation giving volumetric flowrate regardless of specific model as a function of wall shear stress

MHMT 4 Non-Newtonian fluid flow Application RMW equation for power law fluid Friction factor Modified Reynolds number (reduces to standard Re for n=1)

MHMT 4 Non-Newtonian fluid flow Application RMW equation for Bingham fluid Introducing the friction factor and expression for the wall shear stress we obtain Remark: Given pressure drop (therefore w) it is quite easy to calculate flowrate. Reversely: given flowrate the pressure drop must be calculated by solution of algebraic equation of the 4 th order (but there exists graphical representation of the previous equation).

MHMT 4 Non-Newtonian fluid flow Exercise: Derive the RMW equation for the Herschel Bulkley model K-consistency, n-power law index, y-yield stress …. verify that the n=1 reduces to the previously derived Bingham model.

MHMT 4 Non-Newtonian fluid flow Practical importance of RMW equation is in the fact that it enables generalization of experiments with arbitrary liquid, without necessity to identify a specific rheological model. differential pressure transducer 2 R T L pump flow meter Diagram of consistency variables Experimentally determined curves w, are independent of the pipe dimensions, therefore can be used for design of pipelines (with the same liquid and at the same temperature). Remark: different w, curves recorded at different diameters of pipes indicate anomalies, for example wall slip (Mooney analysis), different flow regime (turbulent flow) or experimental errors (insufficient stabilization length of pipe, Bagley correction).

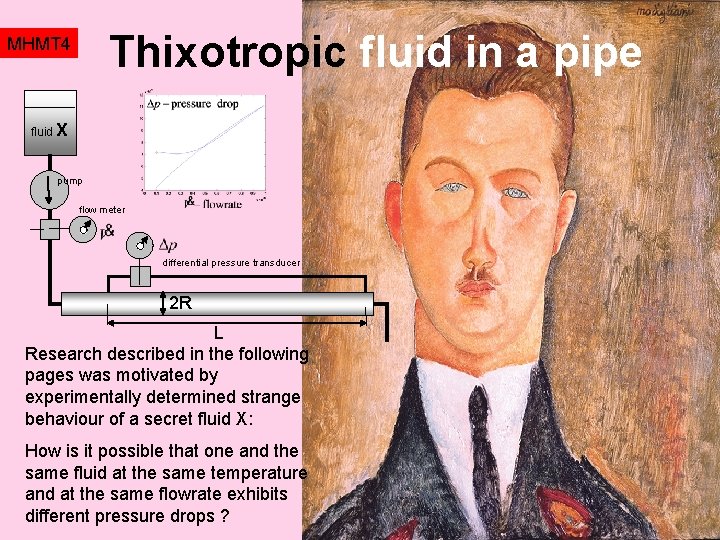
Thixotropic fluid in a pipe MHMT 4 fluid X pump flow meter differential pressure transducer 2 R L Research described in the following pages was motivated by experimentally determined strange behaviour of a secret fluid X: How is it possible that one and the same fluid at the same temperature and at the same flowrate exhibits different pressure drops ?

MHMT 4 Thixotropic fluid in a pipe Thixotropic fluids are characterised by viscosity, which depends upon the deformation history (structure and consistency is affected by shear rate at previous times). Example of constitutive equation of a thixotropic liquid was presented as the HZS model (see previous lecture). Problem of pressure drop of a thixotropic fluid in laminar flow in a circular pipe is usually solved numerically, see the list of relevant papers Ahmadpour A. , Sadeghy K. : An exact solution for laminar, unidirectional flow of Houska thixotropic fluids in a circular pipe. J. of Non-Newtonian Fluid Mechanics, 194 (2013), pp. 23 -31 Corvisier P. , Nouar C. , Devienne R. , Lebouché M. : Development of a thixotropic fluid flow in a pipe. Experiments in Fluids, 31 (2001), pp. 579 -587 Schmitt L. , Ghnassia G. , Bimbenet J. J. , Cuvelier G. : Flow properties of stirred Youghurt: Calculation of the pressure drop for a thixotropic fluid. J. Food Eng. 37 (1998), pp. 367 -388 Escudier M. P. , Presti F. : Pipe flow of a thixotropic liquid. J. Non-Newtonian Fluid Mech. , 62 (1996), pp. 291 -306 Billingham J. , Fergusson J. W. J. : Laminar unidirectional flow of a thixotropic fluid in a circular pipe. J. of Non-Newtonian Fluid Mech. , 47 (1993), pp. 21 -55 Kemblowski Z. , Petera J. : Memory effects during the flow of thixotropic fluids in pipes. Rheol. Acta 20, (1981), pp. 311 -323 Sestak J. , Zitny R. , Houska M. : Změny vlastností tixotropních látek v průběhu zpracování. In 21. konf. SSCh. I, Vyhne ° 1994 (HZS model, evaluation of structural parameter change in a continuous system of series of ideally mixed vessels) Sestak J. , Zitny R. , Houska M. : Dynamika tixoropnich kapalin. Rozpravy CSAV Praha 1990 Sestak J. , Zitny R. , Houska M. : Simple rheological models of food liquids for process design and quality assessment. Journal of Food Engineering, 1983, pp. 35 -49 (thixotropic integral model Zitny, and differential model HZS) Sestak J. , Houska M. , Zitny R. : Mixing of thixotropic fluids. Journal of Rheology, 1982, pp. 459 -475 Zitny R. : Nestacionární tok tixotropní kapaliny v trubce. Acta polytechnica, 1977, pp. 95 -102 (integral model of thixotropy solved by assuming that the structural parameter depends only upon time and axial coordinate) Zitny R. : Vliv dissipace a tixotropie na tok nenewtonskych kapalin v trubce. Disertation CVUT 1977 Sestak J. , Zitny R. : Tok tixotropni kapaliny v trubce. Acta Polytechnica, 1976, pp. 45 (integral model of thixotropy, pressure drop calculated from correlation where is Deborah number, ratio of relaxation and process time)

MHMT 4 Thixotropic fluid in a pipe The HZS model of thixotropic fluids is represented by the Herschel Bulkley constitutive equation (a combination of power law liquid with a consistency coefficient K and power law index n and Bingham liquid with a yield stress y ) Structural parameter =1 describes fully recovered inner structure (and high consistency of liquid), while =0 corresponds to completely destroyed structure (and minimum consistency K and yield stress). Time changes of are described by There exist many different modifications and interpretations, for example the latest work, Ahmadpour (2013), assumes only partial and not the material time derivative on the left side, the diffusion term on the right side is considered only by Billingham and Fergusson (1993) in a generalized Moore’s model of thixotropy.

MHMT 4 Thixotropic fluid in a pipe The tensorial form of the HZS model can be simplified for the special case of unidirectional simple shear flow to scalar equations for the shear stress and the shear rate Complete solution of a creeping laminar flow in a pipe should calculate axial as well as radial profiles of velocity and structure parameter based upon linearity of radial shear stress profile u(t, r, x) = w r/R R A great simplification would be assumption that the depends only upon the axial coordinate and time, (t, x). This assumption can be accepted only if the flow is so slow that the diffusion in the radial direction has enough time to equalize the radial profile of and that the problem of -transport with a nonuniform radial velocity profile can be substituted by a model with “plug flow” (constant velocity) and modified diffusion in the axial direction (model of axial dispersion, which will be discussed later – lecture on mass transport)

MHMT 4 Thixotropic fluid in a pipe For independent of radial coordinate it is possible to apply RMW (Rabinowitsch, Mooney, Weissenberg) equation with We need to calculate pressure drop (dp/dx=2 w/R) for given flowrate therefore it is necessary to invert the previous equation Remark: Iterative evaluation is necessary, but is fast and convergent for arbitrary n, K, y

MHMT 4 Thixotropic fluid in a pipe If the structural parameter depends only upon x and time and if we neglect the axial dispersion term the evolution of is described by hyperbolic partial differential equation which can be integrated analytically along characteristic dx=u. dt as soon as the velocity and shear rate are constant (t) is value of structural parameter of a fluid particle having value 0 at time t 0 (assuming that the particle is under action of constant shear rate).

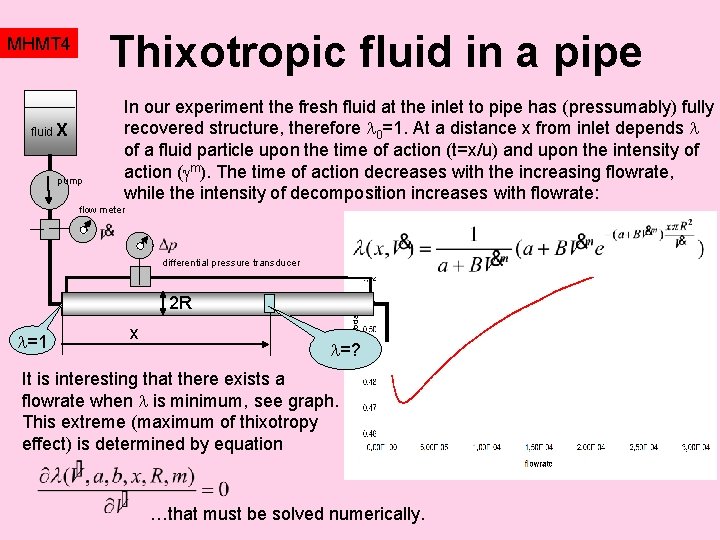
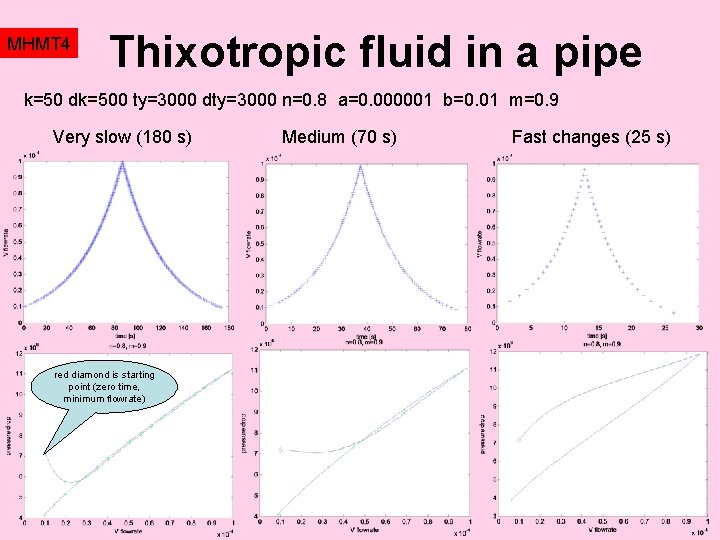
Thixotropic fluid in a pipe MHMT 4 fluid X pump In our experiment the fresh fluid at the inlet to pipe has (pressumably) fully recovered structure, therefore 0=1. At a distance x from inlet depends of a fluid particle upon the time of action (t=x/u) and upon the intensity of action ( m). The time of action decreases with the increasing flowrate, while the intensity of decomposition increases with flowrate: flow meter differential pressure transducer 2 R =1 x =? It is interesting that there exists a flowrate when is minimum, see graph. This extreme (maximum of thixotropy effect) is determined by equation …that must be solved numerically.

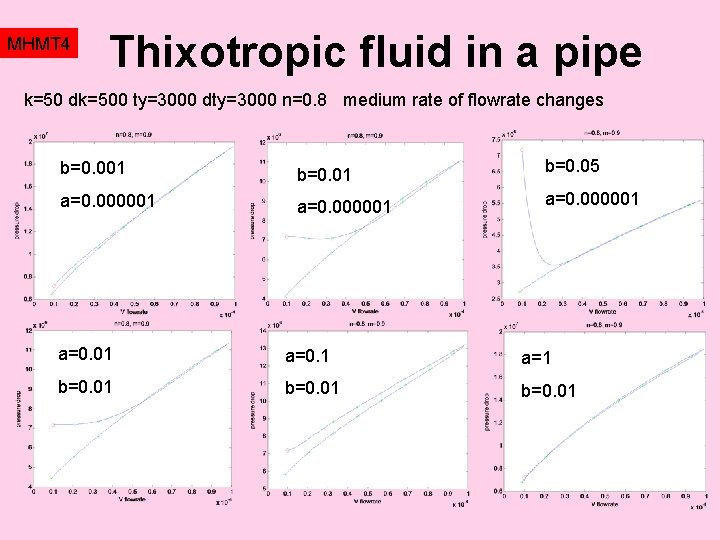
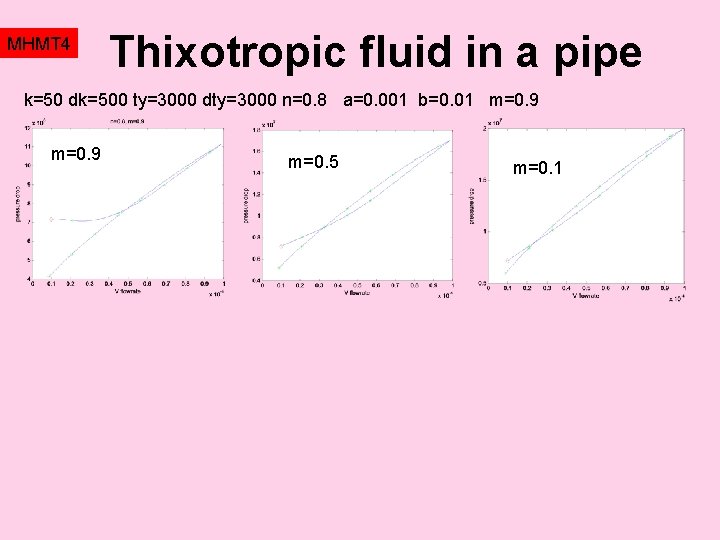
MHMT 4 Thixotropic fluid in a pipe Resulting expressions (for example expressions for friction factor, for structural parameter, etc) are usually formulated in terms of dimensionless parameters, Debora number, thixotropy number, Bingham number and other, see for example Billingham, Fergusson (1993). Deborah number De is the ratio of thixotropic time scale and the process time. The thixotropic number Tx is just the ratio of decay and bildup terms. The „optimum flowrate“ condition can be expressed generally as …and for the special case m=1, the Debora number at maximum tixotropy goes to infinity. Nontrivial optimum exists only for m<1. Example: a=b=0. 01, m=0. 9, R=0. 01, x=1 optimum at De=1, Tx=5. 3 (therefore flowrate 2. 10 -5 m 3/s)

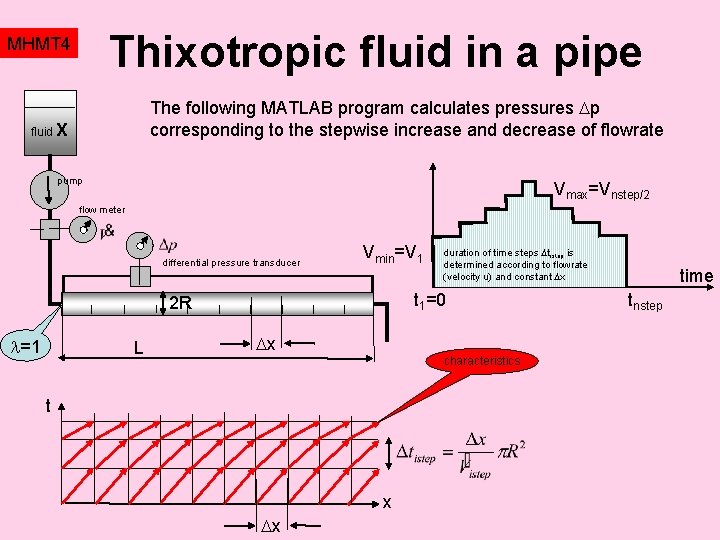
Thixotropic fluid in a pipe MHMT 4 The following MATLAB program calculates pressures p corresponding to the stepwise increase and decrease of flowrate fluid X pump Vmax=Vnstep/2 flow meter differential pressure transducer Vmin=V 1 t 1=0 2 R =1 L duration of time steps tistep is determined according to flowrate (velocity u) and constant x x characteristics t x x time tnstep

MHMT 4 Thixotropic fluid in a pipe % simulation (flowrate up and down) l=3; %length of pipe r=0. 01; %radius nx=50; nstep=150; k=50; dk=500; ty=3000; dty=3000; n=0. 8 % Herschel Bulkley a=0. 000001; b=0. 01; m=0. 9; % HZS thixotropy model vmin=1 e-5; vmax=1 e-4; % min, max. flowrate x=linspace(0, l, nx); dx=l/(nx-1); % time sequence of flowrate and corresponding times nstep 2=nstep/2; dv=(vmax-vmin)/nstep 2; v(1)=vmin; time(1)=0; for i=2: nstep 2 v(i)=v(i-1)+dv; time(i)=time(i-1)+dx*3. 141*r^2/v(i-1); end for i=nstep 2+1: nstep v(i)=v(i-1)-dv; time(i)=time(i-1)+dx*3. 141*r^2/v(i-1); end lamx(1: nx)=1; [dp(1), taux]=dpa(k, dk, ty, dty, n, v(1), r, lamx, nx, dx); [dt, lam]=lamnew(a, b, m, v(1), r, lamx, nx, dx); figure(3) hold off for istep=2: nstep lamx(1: nx)=lam(1: nx); [dp(istep), taux]=dpa(k, dk, ty, dty, n, v(istep), r, lamx, nx, dx); [dt, lam]=lamnew(a, b, m, v(istep), r, lamx, nx, dx); if mod(istep, 40)==0 plot(x(1: nx), lam(1: nx)) hold on end figure(1) plot(time(1: nstep), v(1: nstep)) figure(2) hold off plot(v(1: nstep), dp(1: nstep)) hold on plot(v(1), dp(1), 'rd') function [dt, lam]=lamnew(a, b, m, vdot, r, lamx, nx, dx) % vector of structural parameters lam(1. . nx) at time tnew % inlet value is always lam(1)=1 (fresh fluid) % a, b, m model parameters (see model HZS) u=vdot/(3. 141*r^2); gamma=vdot/(3. 141*r^3); lam(1)=1; dt=dx/u; gam=gamma^m; for i=1: nx-1 lam(i+1)=(a-(a-(a+b*gam)*lamx(i))*exp(-(a+b*gam)*dt))/(a+b*gam); end function tauw=hb(ty, k, n, vdot, r) % ty-yield stress, k-consistency, n-flow index, vdot-flowrate, r-radius kappa=n/(3*n+1); eps=1 e 10; iter=0; while (iter<50 & eps>1 e-4) iter=iter+1; tauw=ty+k*(vdot/(kappa*3. 141*r^3))^n; t=ty/tauw; kappan=n/(3*n+1)*(1 -t/(2*n+1)-2*n/((n+1)*(2*n+1))*(t^2+n*t^3)); eps=abs(kappa-kappan); kappa=kappan; end function [dp, taux]=dpa(k, dk, ty, dty, n, vdot, r, lamx, nx, dx) % pipe length (nx-1). dx , radius r, flowrate vdot, strict parameter % lam(1), . . . lam(nx) % result: pressure drop dp, vector of wall stresses taux(1). . taux(nx) for i=1: nx taux(i)=hb(ty+lamx(i)*dty, k+lamx(i)*dk, n, vdot, r); end dp=0; for i=1: nx-1 dp=dp+taux(i)*2*dx/r; end

MHMT 4 Thixotropic fluid in a pipe k=50 dk=500 ty=3000 dty=3000 n=0. 8 a=0. 000001 b=0. 01 m=0. 9 Very slow (180 s) red diamond is starting point (zero time, minimum flowrate) Medium (70 s) Fast changes (25 s)

MHMT 4 Thixotropic fluid in a pipe k=50 dk=500 ty=3000 dty=3000 n=0. 8 medium rate of flowrate changes b=0. 001 b=0. 05 a=0. 000001 a=0. 1 a=1 b=0. 01

MHMT 4 Thixotropic fluid in a pipe k=50 dk=500 ty=3000 dty=3000 n=0. 8 a=0. 001 b=0. 01 m=0. 9 m=0. 5 m=0. 1

MHMT 4 EXAM Navier Stokes equations

MHMT 4 What is important (at least for exam) Navier Stokes equations (2 D incompressible) Formulation with vorticity and stream function

MHMT 4 What is important (at least for exam) Drag flow between parallel plates (steady and transient) Penetration depth Flow in a circular pipe Darcy Weisbach, Reynolds number and Mooney diagram

MHMT 4 What is important (at least for exam) Non Newtonian flows RMW equation
 Mhmt
Mhmt Conservation of mass momentum and energy equations
Conservation of mass momentum and energy equations Heat and mass transfer
Heat and mass transfer Fundamental of heat and mass transfer
Fundamental of heat and mass transfer Heat and mass transfer fundamentals and applications
Heat and mass transfer fundamentals and applications Heat and mass transfer
Heat and mass transfer Principle of kettle evaporator
Principle of kettle evaporator Simultaneous heat and mass transfer
Simultaneous heat and mass transfer Heat-mass transfer and geodynamics of the lithosphere:
Heat-mass transfer and geodynamics of the lithosphere: Critical radius of insulation for cylinder
Critical radius of insulation for cylinder Chapter 6 momentum changing momentum
Chapter 6 momentum changing momentum Momentum=mass x velocity
Momentum=mass x velocity Velocity center of mass equation
Velocity center of mass equation Momentum is mass times
Momentum is mass times Ideal fluid
Ideal fluid Center of mass and linear momentum
Center of mass and linear momentum Physics
Physics Momentum=mass x velocity
Momentum=mass x velocity Impulse and momentum relationship
Impulse and momentum relationship An 82 kg male and a 48 kg female
An 82 kg male and a 48 kg female Weather equations
Weather equations Momentum equation
Momentum equation What is disturbance that transfers energy
What is disturbance that transfers energy Heat transfer on metal
Heat transfer on metal 7 fundamental units
7 fundamental units Radiated heat always travels downwards
Radiated heat always travels downwards Heat vs thermal energy
Heat vs thermal energy Energy balance equation heat transfer
Energy balance equation heat transfer Jeopardy conductor
Jeopardy conductor Example of heat transfer by radiation
Example of heat transfer by radiation Energy transfer
Energy transfer A double pipe parallel flow heat exchanger
A double pipe parallel flow heat exchanger Heat transfer overview
Heat transfer overview Design of shell and tube heat exchanger by kern method
Design of shell and tube heat exchanger by kern method Ntu heat transfer
Ntu heat transfer Heat transfer popcorn lab
Heat transfer popcorn lab Radiation examples
Radiation examples Heat transfer on earth
Heat transfer on earth Sunlight melts a wax crayon left outside.
Sunlight melts a wax crayon left outside. Conduction convection radiation examples
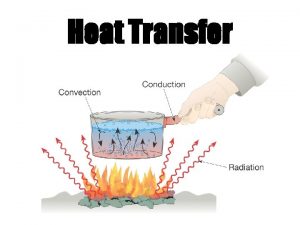
Conduction convection radiation examples What is heat transfer conduction convection and radiation
What is heat transfer conduction convection and radiation Method of heat transfer
Method of heat transfer