MHMT 3 Momentum Heat Mass Transfer Kinematics and

MHMT 3 Momentum Heat Mass Transfer Kinematics and dynamics. Constitutive equations Kinematics of deformation, stresses, invariants and rheological constitutive equations. Fluids, solids and viscoelastic materials. Rudolf Žitný, Ústav procesní a zpracovatelské techniky ČVUT FS 2010

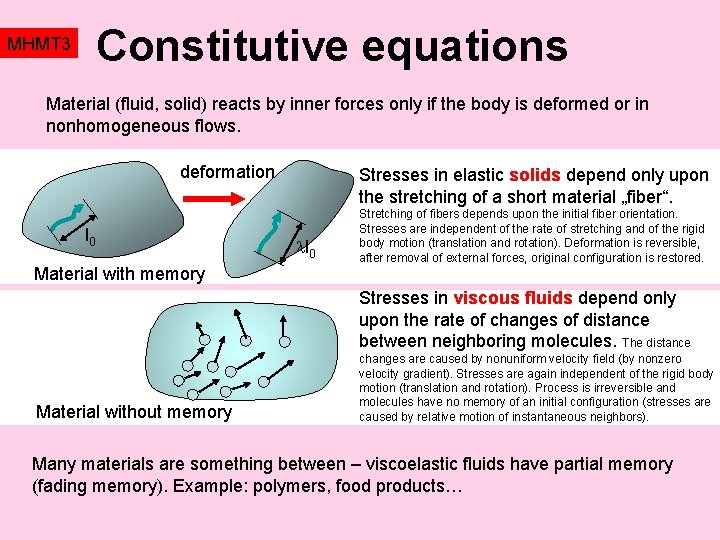
Constitutive equations MHMT 3 Material (fluid, solid) reacts by inner forces only if the body is deformed or in nonhomogeneous flows. deformation l 0 Material with memory Stresses in elastic solids depend only upon the stretching of a short material „fiber“. l 0 Stretching of fibers depends upon the initial fiber orientation. Stresses are independent of the rate of stretching and of the rigid body motion (translation and rotation). Deformation is reversible, after removal of external forces, original configuration is restored. Stresses in viscous fluids depend only upon the rate of changes of distance between neighboring molecules. The distance Material without memory changes are caused by nonuniform velocity field (by nonzero velocity gradient). Stresses are again independent of the rigid body motion (translation and rotation). Process is irreversible and molecules have no memory of an initial configuration (stresses are caused by relative motion of instantaneous neighbors). Many materials are something between – viscoelastic fluids have partial memory (fading memory). Example: polymers, food products…

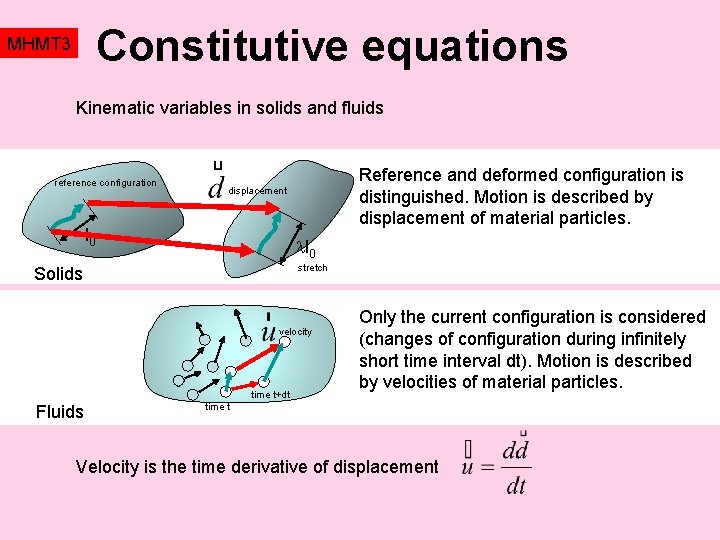
Constitutive equations MHMT 3 Kinematic variables in solids and fluids reference configuration Reference and deformed configuration is distinguished. Motion is described by displacement of material particles. displacement l 0 stretch Solids velocity time t+dt Fluids Only the current configuration is considered (changes of configuration during infinitely short time interval dt). Motion is described by velocities of material particles. time t Velocity is the time derivative of displacement

MHMT 3 Constitutive equations FLUID Motion of viscous fluid is a fully irreversible process, mechanical energy is converted to heat. Fluid has no memory to previous spatial configuration of fluid particle, there is no recoil after unloading external stress. Newton’s law: Macke

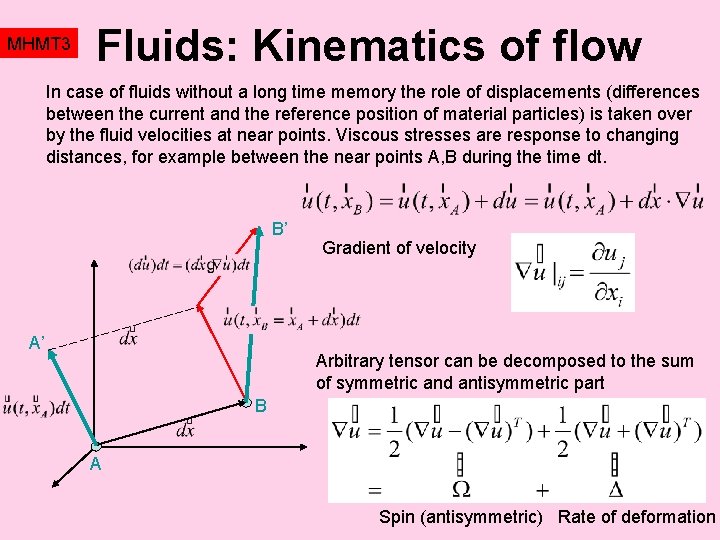
MHMT 3 Fluids: Kinematics of flow In case of fluids without a long time memory the role of displacements (differences between the current and the reference position of material particles) is taken over by the fluid velocities at near points. Viscous stresses are response to changing distances, for example between the near points A, B during the time dt. B’ A’ Gradient of velocity Arbitrary tensor can be decomposed to the sum of symmetric and antisymmetric part B A Spin (antisymmetric) Rate of deformation

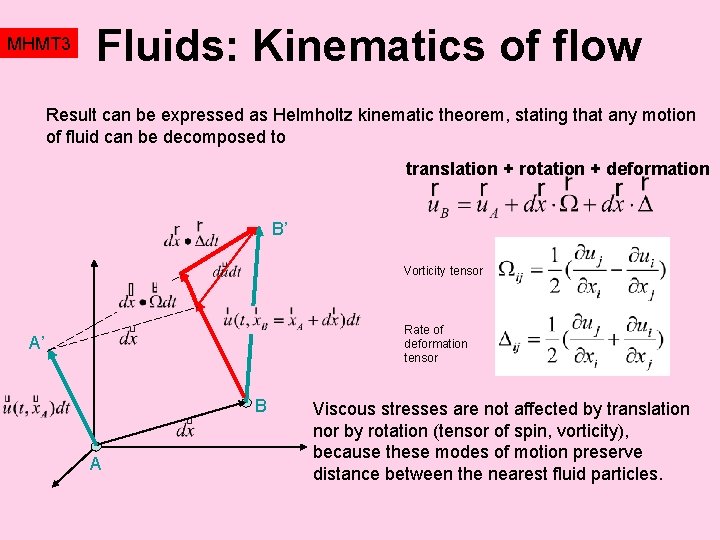
MHMT 3 Fluids: Kinematics of flow Result can be expressed as Helmholtz kinematic theorem, stating that any motion of fluid can be decomposed to translation + rotation + deformation B’ Vorticity tensor Rate of deformation tensor A’ B A Viscous stresses are not affected by translation nor by rotation (tensor of spin, vorticity), because these modes of motion preserve distance between the nearest fluid particles.

MHMT 3 Fluids: stresses Tensor of total stresses can be decomposed to pressure and viscous stresses ØHydrostatic pressure (isotropic, independent of relative motion of fluid particles). For pure fluids the pressure can be derived from thermodynamics relationships, e. g. where u is internal energy and s – entropy. ØViscous stresses are fully described by a symmetric tensor independent of the rigid body motion. Viscous stress is in fact the momentum flux due to molecular diffusion.

MHMT 3 Fluids: Constitutive equations represent a relationship between Kinematics (characterised by the rate of deformation for fluids) Viscous stress (dynamic response to deformation) The simplest constitutive equation for purely viscous (Newtonian) fluids is linear relationship between the tensor of viscous stresses and the tensor of rate of deformation (both tensors are symmetric) Second (volumetric) viscosity [Pa. s] Index notation In terms of velocities Dynamic viscosity [Pa. s]

MHMT 3 Fluids: Constitutive equation The coefficient of second viscosity represents resistance of fluid to volumetric expansion or compression. According to Lamb’s hypothesis the second (volumetric) viscosity can be expressed in terms of dynamic viscosity This follows from the requirement that the mean normal stresses are zero (this mean value is absorbed in the pressure term) Constitutive equation for Newtonian fluids (water, air, oils) is therefore characterized by only one parameter, dynamic viscosity

MHMT 3 Fluids: Constitutive equation Viscosity is a scalar dependent on temperature. Viscosity of gases can be calculated by kinetic theory as =( lmv)/3 (as a function of density, mean free path and the mean velocity of random molecular motion, see the previous lecture) and these parameters depend on temperature. This analysis was performed 150 years ago by Maxwell, giving temperature dependence of viscosity of gases Viscosity of liquids is much more difficult. According to Eyring the liquid molecules vibrate in a “cage” of closely packed neighbors and move out only if an energy barrier is surpassed. This energy level depends upon temperature by the Arrhenius term Viscosity of gases therefore increases and viscosity of liquids decreases with temperature. Typical viscosities at room temperature water=0. 001 Pa. s air=0. 00005 Pa. s

MHMT 3 Fluids: Constitutive equation Viscosity dependent on the rate of deformation and stress. There exist many liquids with viscosity dependent upon the intensity of deformation rate (“apparent” viscosity usually decreases with the increasing shear rate), these liquids are called Øgeneralized newtonian fluids (viscosity depends only upon the actual deformation rate, examples are food liquids, polymers…) There also materials which flow like liquids only as soon as the intensity of stress exceeds some threshold (and below this threshold the material behaves like solid, or an elastic solid) Øyield stress (viscoplastic) fluids (example is toothpaste, paints, foods like ketchup) And there exist also liquids with viscosity dependent upon the whole history of previous deformation, changing an inner structure of liquid in time Øthixotropic fluids (examples are thixotropic paints, plasters, yoghurt). Viscosity (T, t, rate of deformation, stress) is a scalar, so the intensity of deformation and the characteristic stress should be also scalars. However the rate of deformation and the stress are tensors

MHMT 3 Fluids: Invariants How large is a tensor? Magnitude of a stress tensor or intensity of the deformation rate are important characteristics of stress and kinematic state at a point x, y, z, information necessary for constitutive equations but also for decision whether a strength of material was exhausted (do you remember HMH criterion used in the structural analysis? ) and many others. Easy answer to this question is for vectors, it is simply the length of an arrow. Magnitude of a tensor should be independent of the coordinate system, it should be INVARIANT. We will show, that there are just 3 invariants (3 characteristic numbers) in the case of second order tensors, telling us whether the material is compressed/expanded, what is the average value of the rate of deformation, density of deformation energy and so on (it depends upon the nature of tensor).

MHMT 3 Fluids: Invariants Any tensor of the second order is defined by 9 numbers arranged in a matrix. However these numbers depend upon rotation of the coordinate system. For the symmetric tensors (like stress, or deformation tensors) the rotation of coordinate system can be selected in such a way that the matrix representation will be a diagonal matrix ([[ ]], see the first lecture) In view of orthogonality of [[R]] we obtain by multiplying the equation by [[R]]T This is so called eigenvalue problem: given the matrix [[ ]]3 x 3 calculate three eigenvectors (columns of the matrix [[R]]T=[[n 1], [n 2], [n 3]]) and corresponding eigenvalues 1, 2, 3, that satisfy the previous equation.

MHMT 3 Fluids: Invariants The eigenvalue problem can be reformulated to a system of linear algebraic equations for components of the eigenvector This system is homogeneous (trivial solution n 1=n 2=n 3=0) and non-trivial solution exists only if the matrix of system is singular, therefore if Expanding this determinant gives a cubic algebraic equation for eigenvalues

MHMT 3 Fluids: Invariants The values I , III are three principal invariants of tensor . Eigenvalues are also invariants and generally speaking any combination of principal invariants forms an invariant too. For example the second invariant of the deformation rate is frequently expressed in the following form and called intensity of the strain rate (it has a right unit 1/s). Example: at simple shear flow u 1(x 2) 0, u 2=u 3=0 holds shear rate This is also the explanation why the constant 2 was introduced in the previous definition The first and third invariants of rate of deformation are no so important. For example the first invariant of incompressible liquid is identically zero and brings no information neither on shear nor elongational flows.

MHMT 3 Fluids: GNF (power law) Generalised Newtonian Fluids are characterised by viscosity function dependent upon the second invariant of the deformation rate tensor The most frequently used constitutive equation of GNF is the power law model (Ostwald de Waele fluid) K-coefficient of consistency n-flow behavior index Example: for the simple shear flow and incompressible liquid the power law reduces to n=1 Newtonian n<1 pseudoplastic fluid Graph representing relationship between the shear rate and the shear stress is called rheogram ux(y) x

MHMT 3 Fluids: Yield stress (Bingham) Even for fluids exhibiting a yield stress it is possible to preserve the linear relationship between the stress and the rate of deformation tensor (Bingham fluid). Constitutive equation for Bingham liquid (incompressible) can be expressed as (this is von Mises criterion of plasticity) for while for lower stresses the rate of deformation is zero. p-plastic viscosity y=yield stress Example: for the simple shear flow and incompressible liquid the Bingham model reduces to y=0 Newtonian Bingham fluid This is orginal 1 D model suggested by Bingham. The 3 D tensorial extension was suggested by Oldroyd

MHMT 3 Fluids: Thixotropic (HZS) Thixotropic fluids have inner structure, characterised by a scalar structural parameter ( =1 fully restored gel-like structure, while =0 completely destroyed fluid-like structure). Evolution of the structural parameter (identified with the flowing particle) can be described by a kinetic equation, depending upon the history of rate of deformation. a-restoration parameter, b-decay parameter, m-decay index The structural parameter increases at rest exponentially with the time constant 1/a. Rate of structure decay increases with the rate of deformation. Value of the structural parameter determines the actual viscosity or the consistency coefficient of the power law model and the yield stress (Herschel Bulkley) HZS model (Houska, Zitny, Sestak), see Sestak J. , Zitny R. , Houska M. : Dynamika tixoropnich kapalin. Rozpravy CSAV Praha 1990

MHMT 3 Fluids: Rheometry Experimental identification of constitutive models -Rotational rheometers use different configurations of cylinders, plates, and cones. Rheograms are evaluated from measured torque (stress) and frequency of rotation (shear rate). Rotating cylinder Plate-plate, or cone-plate -Capillary rheometers evaluate rheological equations from the experimentally determined relationship between flowrate and pressure drop. Theory of capillary viscometers, Rabinowitch equation, Bagley correction.

MHMT 3 Fluids: Summary Constitutive equations for fluids assume that the stress tensor depends only upon the state of fluid (characterized by the rate of deformation and by temperature) at a given place x, y, z. It is also assumed that the same coefficient of proportionality holds for all components of the viscous stress tensor and the deformation rate tensor, therefore It does not mean that the constitutive equations are always linear because the viscosity can depend upon the deformation rate itself (and there exist plenty of models for viscosity as a function of the second invariants of deformation rate and stresses: power law, Bingham, Herschel Bulkley, Carreau model, naming just a few). Nevertheless, some features are common, for example the absence of normal stresses ( rr, zz, …) as soon as the corresponding component of the deformation rate tensor is zero. The exception are rheological models of the second order, for example (Rivlin), exhibiting features typical for viscoelastic fluids, like normal stresses, secondary flows in channels, nevertheless these models are not so important for engineering practice.

MHMT 3 Solids: Reversible accumulation of external loads to internal deformation energy Time is of no importance, unloaded material recoils immediately to initial configuration. Hook’s law Macke

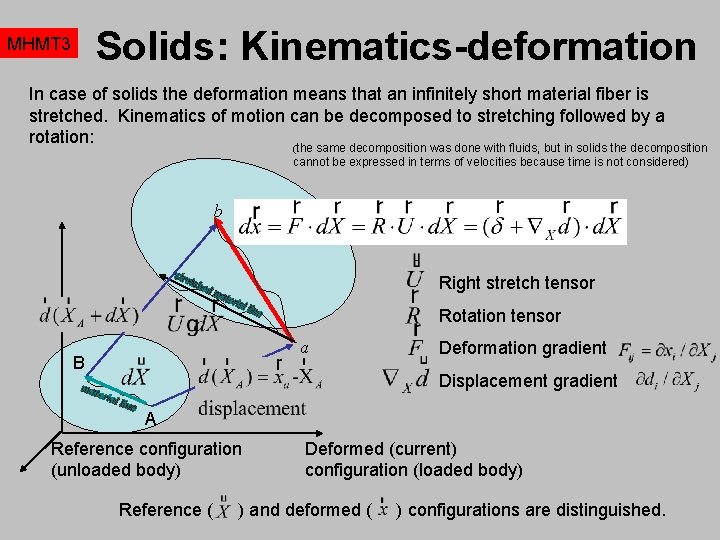
Solids: Kinematics-deformation MHMT 3 In case of solids the deformation means that an infinitely short material fiber is stretched. Kinematics of motion can be decomposed to stretching followed by a rotation: (the same decomposition was done with fluids, but in solids the decomposition cannot be expressed in terms of velocities because time is not considered) b Right stretch tensor Rotation tensor a B Deformation gradient Displacement gradient A Reference configuration (unloaded body) Reference ( Deformed (current) configuration (loaded body) ) and deformed ( ) configurations are distinguished.

MHMT 3 Solids: Kinematics-deformation The stretch tensor U transforms a material fiber d. Xi to the vector Uijd. Xj which is extended or compressed (stretched). Fiber extension can be expressed in terms of the Green-Lagrange strain tensor Eij In the case of small displacements the quadratic term can be neglected and the Green Lagrange tensor of large strains can be approximated by the tensor of small deformations Please notice the perfect analogy with fluids: instead of rate of deformation (gradient of velocities ) there is a deformation (gradient of displacement)

MHMT 3 Solids: Deformation energy The deformation tensors enable calculation of deformation energy (reversibly accumulated in a deformed body) according to different constitutive models. Knowing the deformation energy W as a function of stretches (or deformations) it is possible to calculate the stress tensors as partial derivatives of W, e. g. [stress] [displacement] = [deformation energy change], e. g. W [J/m 3] is deformation energy related to unit volume, ij are components of Cauchy stresses and ij are components of strains. Example: Hook’s law wherefrom the component of stresses can be calculated by partial derivatives E-Young’s modulus of elasticity [Pa], -Poisson’s constant This is the Hook’s law for perfectly elastic linear material

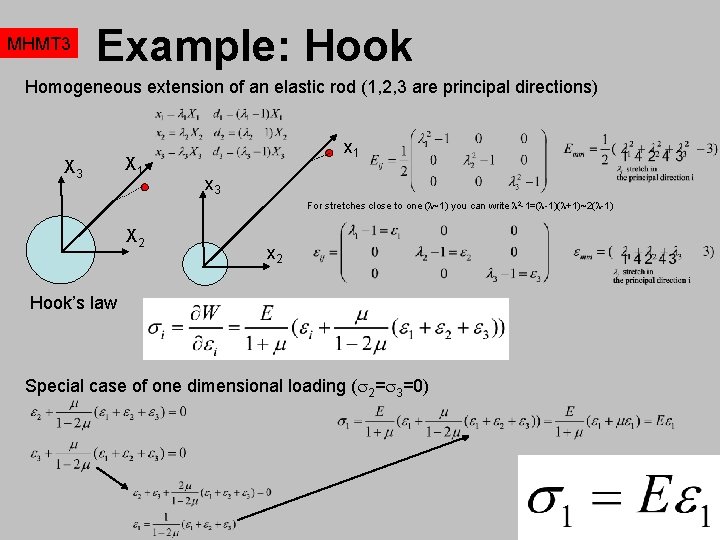
MHMT 3 Example: Hook Homogeneous extension of an elastic rod (1, 2, 3 are principal directions) X 3 X 1 x 3 For stretches close to one ( ~1) you can write 2 -1=( -1)( +1)~2( -1) X 2 x 2 Hook’s law Special case of one dimensional loading ( 2= 3=0)

MHMT 3 Solids: Deformation energy There is a large group of simple constitutive equations based upon assumption that the deformation energy depends only upon the first invariant of the Cauchy Green tensor Then the Cauchy stresses can be expressed as Neo-Hook (linear model similar to Hook, but not the same, has only 1 parameter). Suitable only for description at small stretches (for rubber < 50%) Yeoh model (third order polynomial) Gent model characterised by a limited extensibility of material fibers (Imax is the first invariant corresponding to stretches giving infinite deformation energy) Arruda Boyce model having 7 parameters ( max is a limiting stretch). This is the “ 8 springs” model based upon idea of 8 springs connected in a cube.

MHMT 3 Solids: Experimental methods Biaxial testers Sample in form of a plate, clamped at 4 sides to actuators and stretched ØStatic test ØCreep test ØRelaxation test

MHMT 3 Solids: Experimental methods Inflation tests Tubular samples inflated by inner overpressure. CCD cameras of correlation system Q -450 Pressure transducer ØInternal pressure load ØAxial load ØTorsion Pressurized sample (latex tube) Laser scanner Axial loading (weight) Confocal probe

MHMT 3 Elastic Solids (summary) 1. Relationships between coordinates of material points at reference (X) and loaded (x) configuration must be defined. For example in the finite element method the reference body is a cube and the loaded body is a deformed hexagonal element with sides defined by an isoparametric transformation. 2. Function x(X) enables to calculate components of the deformation gradient F and the Cauchy Green deformation tensor (by multiplication C=FTF) at arbitrary point x, y, z. 3. In terms of the Cauchy Green deformation or strain tensor the density of deformation energy W(C) can be expressed. 4. Components of stress tensors are evaluated as partial derivatives of deformation energy with respect to corresponding components of strain tensor. Anyway, what is typical for solid mechanics, the constitutive equations are expressed in terms of deformation energy W. This is possible because the deformation of elastic solids is a reversible process, time has absolutely no effect upon the stress reactions, and it has a sense to speak about potential of stresses. Nothing like this can be said about fluids, where viscous stresses depend upon the rate of deformation, and viscous friction makes the process irreversible. Therefore the constitutive equations of purely viscous fluids cannot be based upon the deformation energy.

MHMT 3 Viscoelastic FLUIDs Exhibit features of fluids and solids simultaneously. Deformation energy is partly dissipated to heat (irreversibly) and partly stored (reversibly). Both the deformation and the rate of deformation should be considered. Macke

MHMT 3 Viscoelastic FLUIDs The simplest idea of viscoelastic fluids is based upon the spring+dashpot models Maxwell fluids are represented by a serial connection of spring and dashpot These materials are more like fluids, because at constant force F no finite (equilibrium) deformation is achieved. Only during the time changes a part of mechanical work is converted to deformation energy, later on all mechanical work is irreversibly degraded to heat. Voight elastoviscous materials are represented by a parallel connection of spring and dashpot These materials are more like elastic solids. At constant force F finite (equilibrium) deformation is achieved but not immediately. A sudden change of deformation results to infinite force response.

MHMT 3 Viscoelastic FLUIDs Maxwell Viscoelastic fluids of the Maxwell body (serially connected spring and dashpot) can be described by ordinary differential equations (k-stiffness of spring, z attenuation) k x 1 z giving after elimination of x 1 x F This 1 D mechanical model is the basis of the Maxwell model where is a relaxation time, the time required for the stress to relax to (1/e) value of the initial stress jump (due to sudden extension).

MHMT 3 Viscoelastic FLUIDs Maxwell There exist many objections about the previous generalisation of the Maxwell model, first of all against the way how the time derivative of the stress tensor was evaluated. k Time derivative does not fulfill the principle of material objectivity, which means that the time derivative depends upon to motion of observer (material objectivity requires, that even the time derivatives should satisfy the tensor transformation rules [[A’]]=[[R]]. [[A]]. [[R]]T ). The material objectivity is satisfied either by the model x 1 z x F or by the upper convected Maxwell (UCM) Remark: Both lower and upper convective Maxwell models are acceptable from the point of view of mathematical requirements, but they are not the same. The UCM model prevails in practice, at least in papers on polymer melts rheology.

MHMT 3 Viscoelastic FLUIDs Maxwell Example: Fiber spinning (steady elongation flow of a polymer extruded from a dye). Axial velocity w is determined by the radius of fiber R This is continuity equation relating radial u and axial w velocity (cylindrical coordinate system) R and this is a simplified solution based upon assumption of linear radial velocity profile L z Normal stresses for the upper convected Maxwell F This is the system of two ODE for the two unknown normal stresses zz and rr. Given axial force F it is possible to calculate axial profile of thickness R(z) see also the paper Tembely M. et al, Journal of Rheology vol. 56 (2012), pp. 159 -183, fiber spinning using Oldroyd-B and the structural FENE CR rheological model (you will see close similarity of equations presented here).

MHMT 3 Viscoelastic FLUID integral models Let us assume a fluid particle moving along a streamline: x 3 particle at time t rate of strain (e. g. rate of elongation in 1 D case) particle at a past time t’ x 2 x 1 Viscous fluids: stress depends only upon the rate of deformation at the current time t Thixotropic fluids: stress depends also only upon the current rate of deformation but viscosity is affected by the deformation history Viscoelastic fluids: stress at time t is a weighted sum of stresses corresponding to the history of deformation rates. Stress tensors calculated at previous positions of particle must be recalculated to the present position.

MHMT 3 Viscoelastic FLUID Boltzmann Integral viscoelastic models are based upon the Boltzmann superposition principle. The idea can be expressed for 1 D case (a dashpot, taking into account only scalar stress and rate of strain) in form of integral strain rate memory function The monotonically decreasing memory function describes the rate of relaxation (rearrangement of fibers, entanglements…) and can be identified from the unidirectional relaxation experiments. i-relaxation times, ai-relaxation moduli The unidirectional model can be extended to 3 D for example as

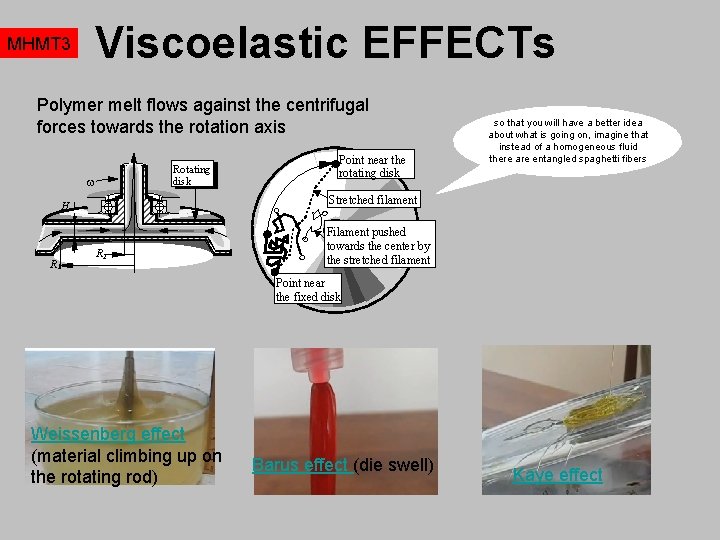
Viscoelastic EFFECTs MHMT 3 Polymer melt flows against the centrifugal forces towards the rotation axis Rotating disk w Stretched filament H R 1 Point near the rotating disk so that you will have a better idea about what is going on, imagine that instead of a homogeneous fluid there are entangled spaghetti fibers R 2 Filament pushed towards the center by the stretched filament Point near the fixed disk Weissenberg effect (material climbing up on the rotating rod) Barus effect (die swell) Kaye effect

MHMT 3 Experiments: solid and fluids Characteristic features of elastic, viscoelastic and viscous liquids are best seen using oscillating rheometer (usually cone and plate configuration) Sinusoidaly applied stress and measured strain (not the rate of strain!) Hookean solid-stress is in phase with Viscoelastic material – phase shift strain (phase shift =0) 0< <90 Viscous liquid- zero stress corresponds to zero strain rate (maximum ) =900 Weissenberg rheogoniometer from Wikipedia

MHMT 3 EXAM Constitutive equations

MHMT 3 What is important (at least for exam) Fluids You should know Helmholtz decomposition of the velocity gradient tensor into spin and rate of deformation tensors Decomposition of stress tensor Newtonian fluid

MHMT 3 What is important (at least for exam) Non Newtonian Fluids Invariants Power law liquids Bingham liquids

MHMT 3 What is important (at least for exam) Solids Deformation gradient (what is it x and X? ) Decomposition of deformation to stretch and rotation tensors (what is it R and U? ) Cauchy Green deformation tensor Hook’s law in terms of Kirchhoff stresses and Cauchy Green deformation tensor (what is it E and ? )

MHMT 3 What is important (at least for exam) Viscoelastic fluids Maxwell model (draw a combination of dashpots and springs corresponding to this model)