MHMT 10 Momentum Heat Mass Transfer Heat transferconduction

MHMT 10 Momentum Heat Mass Transfer Heat transferconduction Multidimensional heat conduction problems. Fins and heat conduction with internal sources or sinks. Unsteady heat conduction in solids. Penetration theory. Rudolf Žitný, Ústav procesní a zpracovatelské techniky ČVUT FS 2010

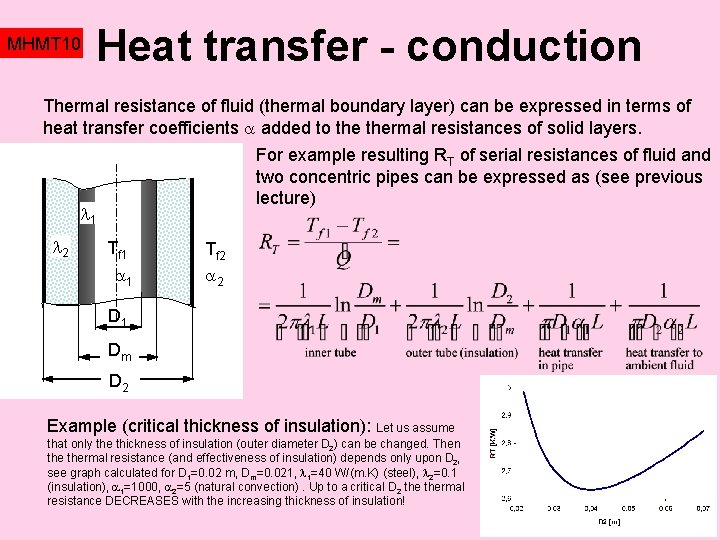
MHMT 10 Heat transfer - conduction Thermal resistance of fluid (thermal boundary layer) can be expressed in terms of heat transfer coefficients added to thermal resistances of solid layers. For example resulting RT of serial resistances of fluid and two concentric pipes can be expressed as (see previous lecture) 1 2 Tf 1 1 Tf 2 2 D 1 Dm D 2 Example (critical thickness of insulation): Let us assume that only the thickness of insulation (outer diameter D 2) can be changed. Then thermal resistance (and effectiveness of insulation) depends only upon D 2, see graph calculated for D 1=0. 02 m, Dm=0. 021, 1=40 W/(m. K) (steel), 2=0. 1 (insulation), 1=1000, 2=5 (natural convection). Up to a critical D 2 thermal resistance DECREASES with the increasing thickness of insulation!

MHMT 10 Heat transfer - conduction Thermal resistance of a composite tube with circular or spiral fins attached to outer tube (fins can be also an integral part of the outer tube). 2 1 Resulting thermal resistance is calculated according to almost the same expression as in the previous case Tf 1 1 Tf 2 2 D 1 Dm D 2 with the only but very important difference: Instead of the outer surface of plain tube D 2 L is used the overall outer surface of fins S 2 L. Such a modification assumes that the 2 on the surface of fins is the same as on the surface of tube and first of all that thermal resistance of fin itself is negligible (simple speaking it is assumed that the fin is made of material having infinite value of thermal conductivity ).

MHMT 10 Heat transfer - conduction The assumption of perfectly conductive fin is unacceptable and in reality thermal resistance of fin must be respected by multiplying the surface S 2 by fin’s efficiency fin which depends upon thermal conductivity of fin, its geometry (thickness and height) and also upon the heat transfer coefficient 2. Tw , Tf b T(x) x dx Efficiency of a thin rectangular fin can be derived easily by solution of temperature profile along the height of fin This is FK equation with a source term, representing heat transfer from both sides of surface (2 dx) to the control volume (bdx) with boundary conditions at the heel of fin (T(x=0)=Tw) and at top of fin d. T/dx=0 (there is no heat flux at x=H) H Efficiency of fin is calculated from temperature gradient at the heel of fin (the gradient determines heat flux at the heel)

MHMT 10 Conduction - nonstationary

MHMT 10 Conduction - nonstationary Temperature distribution in unsteady case generally depends upon time t and coordinates x, y, z. Sometimes, when the temperature distribution is almost homogeneous inside the whole body, the partial differential Fourier Kirchhoff equation reduces to an ordinary differential equation. This simplification is correct if thermal resistance of solid is much less than thermal resistance of fluid, more specifically if Biot number is small enough here D is a characteristic diameter of a solid object and s is thermal conductivity of solid Fourier Kirchhoff equation can be integrated over the whole volume of solid which reduces to ordinary dif. equation as soon as Ts depends only on time

MHMT 10 Conduction - nonstationary As soon as the Biot number is large (Bi>0. 1, therefore if the solid body is too big, for example semi-infinite space) it is necessary to solve the parabolic partial differential Fourier Kirchhoff equation. For the case that the solid body is homogeneous (constant thermal conductivity, density and specific heat capacity) and without internal heat sources the FK equation reduces to The coefficient of temperature diffusivity a= / cp is the ratio of temperature conductivity and thermal inertia with the boundary conditions of the same kind as in the steady state case and with initial conditions (temperature distribution at time t=0). This solution T(t, x, y, z) can be expressed for simple geometries in an analytical form (heating brick, plate, cylinder, sphere) or numerically in case of more complicated geometries.

MHMT 10 Conduction - nonstationary Start up flow of viscous liquid in halfspace (solved in lecture 4) was described by equation which is identical with the Fourier Kirchhoff equation for one dimensional temperature distribution in halfspace and with the step change of surface temperature as a boundary condition: T(t=0, x)=T 0 T(t, x=0)=Tw Exactly the same solution as for the start up flow (complementary error function erfc) holds for dimensionless temperature Tw t T 0 δ x

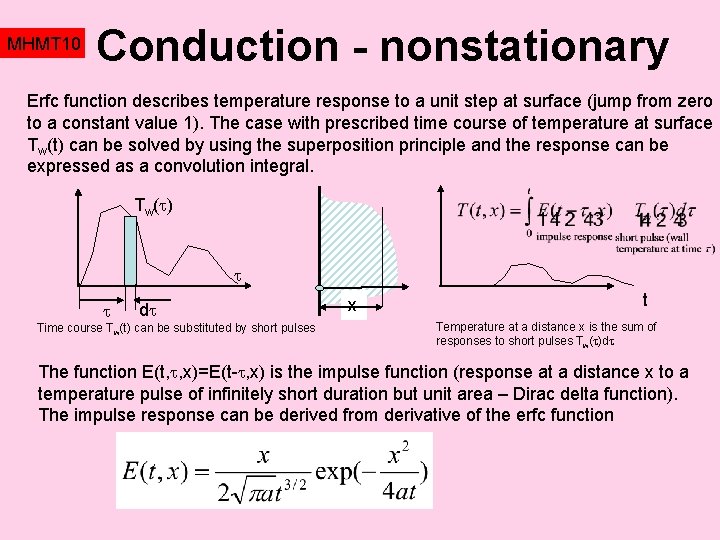
MHMT 10 Conduction - nonstationary Erfc function describes temperature response to a unit step at surface (jump from zero to a constant value 1). The case with prescribed time course of temperature at surface Tw(t) can be solved by using the superposition principle and the response can be expressed as a convolution integral. Tw( ) d Time course Tw(t) can be substituted by short pulses x t Temperature at a distance x is the sum of responses to short pulses Tw( )d The function E(t, , x)=E(t- , x) is the impulse function (response at a distance x to a temperature pulse of infinitely short duration but unit area – Dirac delta function). The impulse response can be derived from derivative of the erfc function

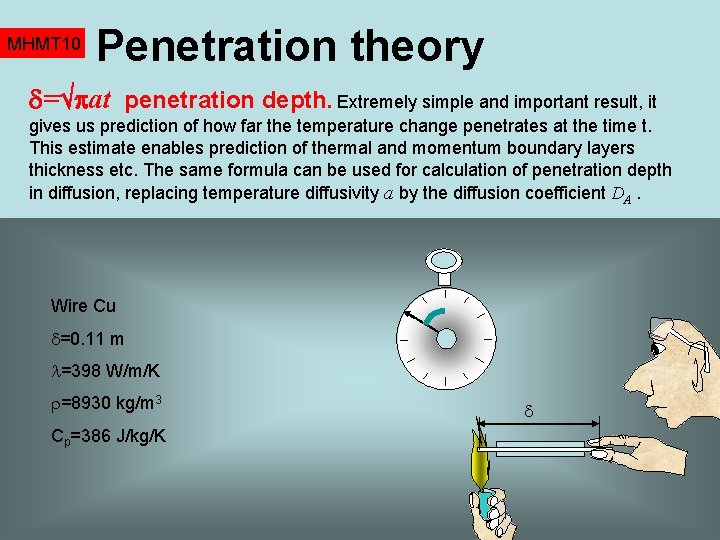
MHMT 10 Penetration theory Still too complicated? Your pocket calculator is not equipped with the erffunction? Use the acceptable approximation by linear temperature profile, (exactly the same procedure as with the start up flow in a half-space) Tw Integrate Fourier equations (up to this step it is accurate) t T 0 t+ t x Approximate temperature profile by line δ +Δ Result is ODE for thickness as a function of time Using the exact temperature profile predicted by erffunction, the penetration depth slightly differs = ( at)

MHMT 10 Penetration theory = at penetration depth. Extremely simple and important result, it gives us prediction of how far the temperature change penetrates at the time t. This estimate enables prediction of thermal and momentum boundary layers thickness etc. The same formula can be used for calculation of penetration depth in diffusion, replacing temperature diffusivity a by the diffusion coefficient DA. Wire Cu =0. 11 m =398 W/m/K =8930 kg/m 3 Cp=386 J/kg/K

MHMT 10 Penetration theory and The penetration theory can be applied also in the case that the semi-infinite space is in contact with fluid and surface temperature depends upon temperature of fluid and the heat transfer coefficient Tf Tw Derive the result as a homework t T 0 δ +Δ t+ t x

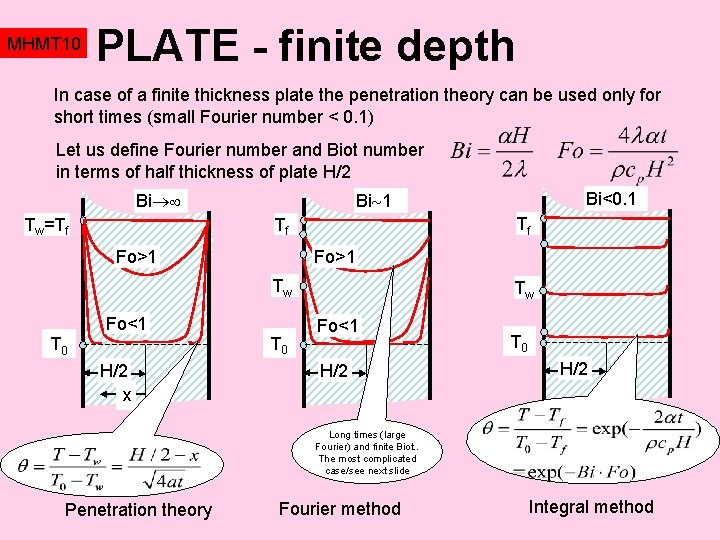
MHMT 10 PLATE - finite depth In case of a finite thickness plate the penetration theory can be used only for short times (small Fourier number < 0. 1) Let us define Fourier number and Biot number in terms of half thickness of plate H/2 Tf Tf Tw=Tf Fo>1 Tw Fo<1 T 0 H/2 x Bi<0. 1 Bi Tw Fo<1 H/2 T 0 H/2 Long times (large Fourier) and finite Biot. . The most complicated case/see next slide Penetration theory Fourier method Integral method

MHMT 10 PLATE - finite depth Fourier method Using dimensionless temperature , distance , time (Fourier number) and dimensionless heat transfer coefficient Bi (Biot number) the Fourier Kirchhoff equation, boundary and initial conditions are transformed to Bi 1 Fourier method is based upon superposition of solutions satisfying differential equation Tf Tw T 0 t H/2 x and boundary conditions

MHMT 10 PLATE - finite depth Spatial component Gi( ) follows from The function cos( ) automatically satisfies the boundary condition at =0 for arbitrary . The boundary condition at wall is satisfied only for yet undetermined values , roots of transcendental equation and this equation must be solved numerically, giving infinite series of roots 1, 2, … These eigenvalues i determine also the temporary components Fi Final temperature distribution is the infinite series of these elementary solutions

MHMT 10 PLATE - finite depth The coefficients ci are determined by the initial condition To solve the coefficients ci from this identity (which should be satisfied for arbitrary ) it is convenient to utilise orthogonality of functions Gi( ) and Gj( ) that follows from original ordinary differential equations and boundary conditions for i j therefore giving final temperature profile

MHMT 10 PLATE/CYLINDER/SPHERE Unsteady temperature profiles inside a sphere and infinitely long cylinders can be obtained in almost the same way, giving temperature profiles in form of infinite series where and only eigenvalues I have to be calculated numerically. This form of analytical solution is especially suitable for description of temperature field at longer times, because exponential terms quickly decay and only few terms in the series are necessary. For shorter times the penetration theory can be applied effectively This analytical solution is presented in the book Carslaw H. S. , Yeager J. C. : Conduction of Heat in Solids. Oxford Sci. Publ. 2 nd Edition, 2004

MHMT 10 3 D – brick, finite cylinder… It is fantastic that an unsteady temperature field in the finite 2 D or 3 D bodies can be obtained in the form of PRODUCT of 1 D solutions expressed in terms of dimensionless temperatures x y z !!! y For example the temperature distribution x in an infinitely long rod with rectangular cross section hx x hy is calculated as hy hx Proof: …and you see that the FK equation is satisfied if x y are solutions of 1 D problem.

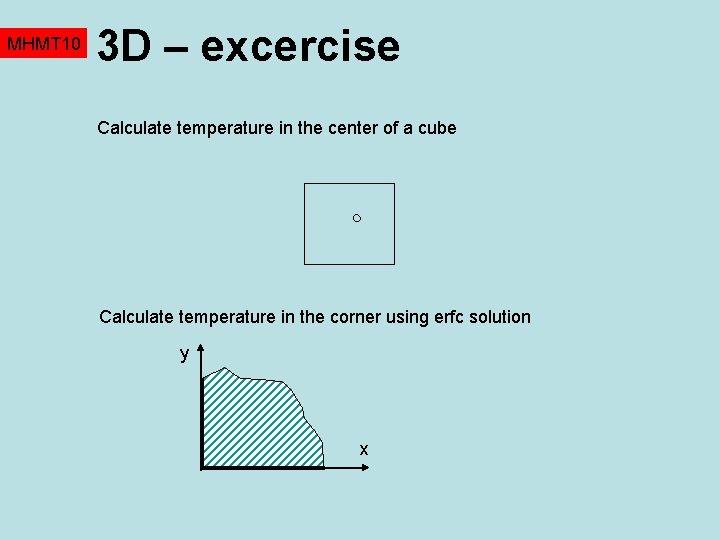
MHMT 10 3 D – excercise Calculate temperature in the center of a cube Calculate temperature in the corner using erfc solution y x

MHMT 10 EXAM Fins and Unsteady heat conduction

MHMT 10 What is important (at least for exam) Thermal resistance of finned tube Efficiency of a planar fin

MHMT 10 What is important (at least for exam) Unsteady heat conduction Transient heating of a semi-infinite space Simplified solution by penetration depth Temperature response to variable surface temperature

MHMT 10 What is important (at least for exam) Find solution of equation for Dirichlet boundary condition at =1 and Neumann boundary condition at =0 Why is it necessary to use dimensionless temperatures in the “product” solution of 2 D and 3 D problems?