Route Finding A Quantum Non Algorithm Jason Clemons

Route Finding: A Quantum [Non] Algorithm Jason Clemons EECS 598 November 7, 2001

The Paper Narayanan, A. , Wallace, J. A Quantum Algorithm for Route Finding. Proceedings of the 15 th European Meeting on Cybernetics and Systems Research (EMCSR 2000), Vienna, Austria, 25 -28 April 2000, Vol. 1, pp 140 -143.

Outline for the day Introduction to Graphs Review of basic graphs l Review of representation l The QAND The Basic Algorithm Interesting Findings Final Thoughts and Questions

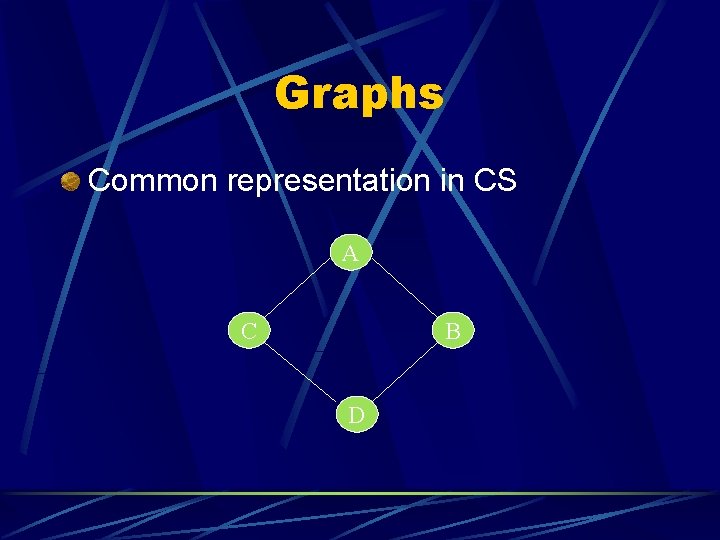
Graphs Common representation in CS A C B D

Graphs Terminology Edges – connect two nodes l Node – Basic state or representation there of l Weight – Cost associated with a node l

Graphs A few characteristics: Weighted l Directional l Problems from graphs Graph Coloring l Hamiltonian Circuit Finding l Traveling Salesman (Shortest Route) l

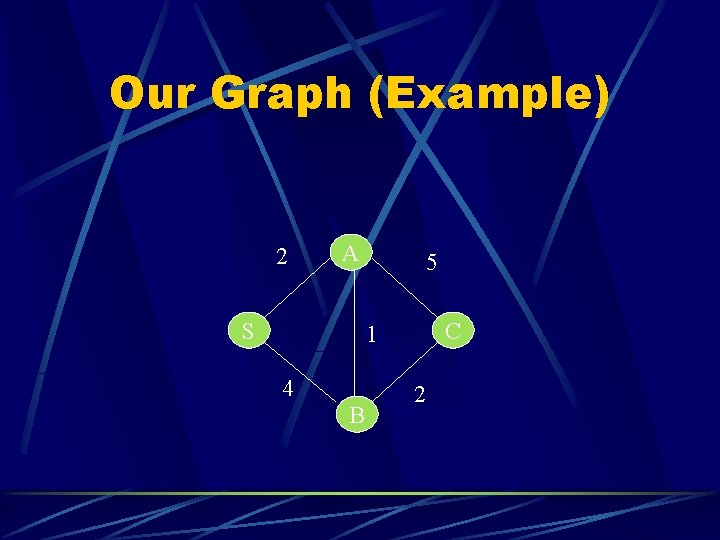
Our Graph Shortest Route Finding for: Weighted finite edges l Finite number of nodes l Undirected l No self connection edges l

Our Graph (Example) 2 A S 5 C 1 4 B 2

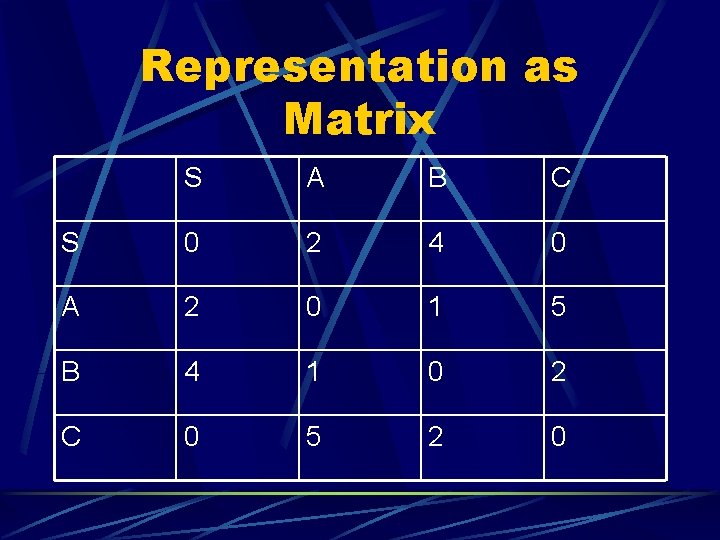
Representation As Matrix Adjacency Matrix: N x N Matrix where N is the number of nodes l Mij = wi to j where w is the weight of the edge from node I to node J and zero or zero if there is no edge l

Representation as Matrix S A B C S 0 2 4 0 A 2 0 1 5 B 4 1 0 2 C 0 5 2 0

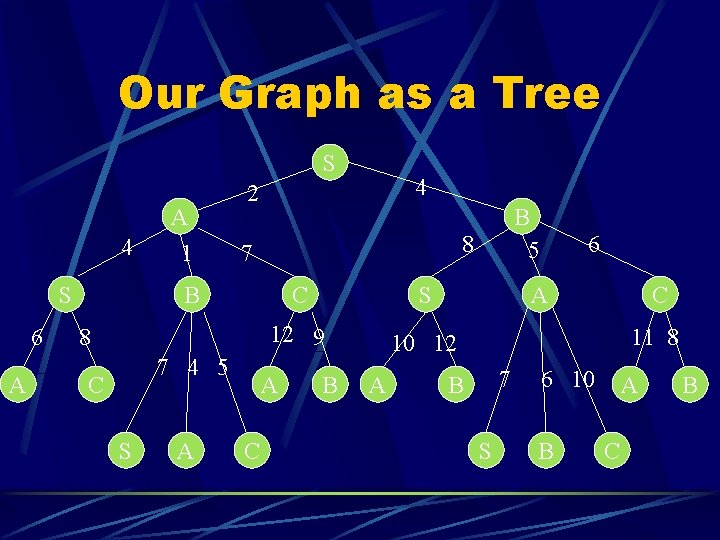
Our Graph as a Tree S A 4 S 6 A 1 8 7 4 5 S A C S 12 9 10 12 A C B 5 8 7 B C 4 2 B A 6 A C 11 8 7 B S 6 10 B A C B

The Quantum And a QSUMAND b = a + b if (a > 0 and b >0) 0 if a=0 or b =0 where a, b R+ {0} Example: 2 QSUMAND 2 = 4 l 2 QSUMAND 0 = 0 l

The Matrix creation Each Row is superposition of states representing the edges l Example: l From our Matrix before the row |S> is the vector a|000> + b|010> +c|100> + d|000> An element can be identified using the row and column labels l Example: <A 1|b 1> = 1 (note: not an IP)

Quantum Registers Similar to what is used by Shor 3 Registers l l l Reg 1 Holds the original adjacency matrix Reg 2 Holds Matrix created when choose start node Reg 3 Interacts with Reg 1 to tell us whether a route exists. During the Algorithm we alternate between Reg 2 and Reg 3 to hold info

Algorithm Step 1 Select the Starting node and perform the QSUMAND manipulation process (Perform QSUMAND between start node row and all other rows) to produce a new matrix M 2

Algorithm Step 1 |S 1>QSUMAND|S 1> l |0 2 4 0> QSUMAND |0 2 4 0> = |0 4 8 0> |S 1>QSUMAND|A 1> l |0 2 4 0> QSUMAND |2 0 1 5> = |0 0 5 0> |S 1>QSUMAND|B 1> = |0 3 0 0> |S 1>QSUMAND|C 1> = |0 7 6 0>

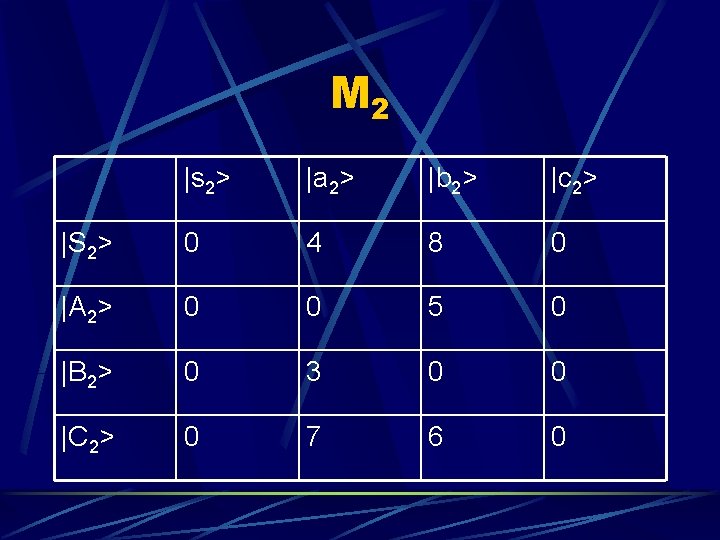
M 2 |s 2> |a 2> |b 2> |c 2> |S 2> 0 4 8 0 |A 2> 0 0 5 0 |B 2> 0 3 0 0 |C 2> 0 7 6 0

What M 2 Says M 2 shows that from S to the row node is connected through column node with a total length of the entry <row|column> l Example: l S to B to A is 5 We have a new level of the search tree!

What M 2 Says The column shows from the start point to that node and from that node to each of the rows.

Algorithm Step 2 Manipulate each non-zero column of the matrices constructed in previous step by performing QSUMAND with each non zero column and the entire row in matrix M 1 that is associated with each element from the non zero column

Step 2 example <S 2|a 2> QSUMAND |S 1> l |4> QSUMAND | 0 2 4 0> = |0 6 8 0> <A 2|a 2> QSUMAND |A 1> = |0 0 0 0> <B 2|a 2> QSUMAND |B 1> = |7 4 0 5> <C 2|a 2> QSUMAND |C 1> = |0 12 9 0>

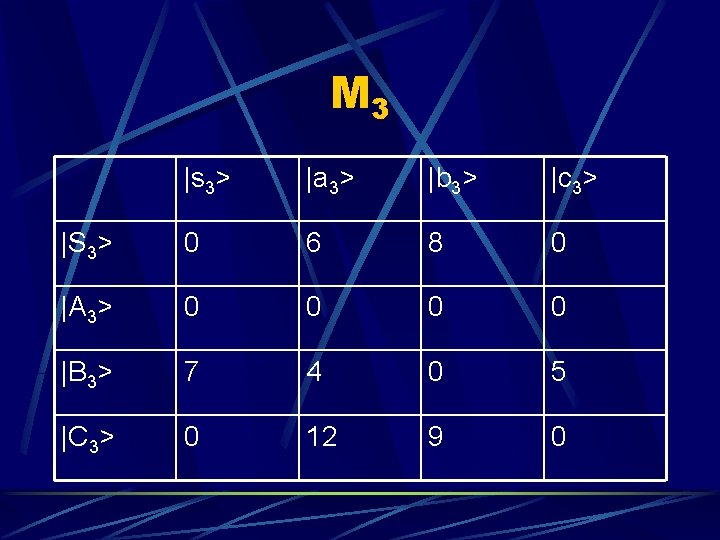
M 3 |s 3> |a 3> |b 3> |c 3> |S 3> 0 6 8 0 |A 3> 0 0 |B 3> 7 4 0 5 |C 3> 0 12 9 0

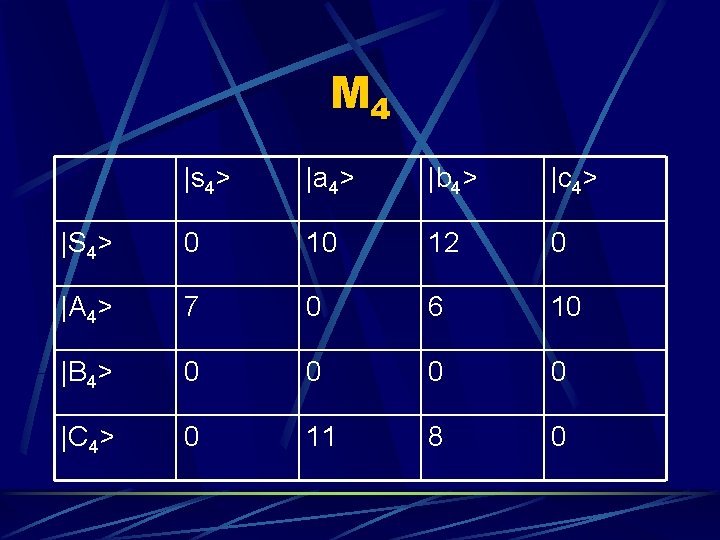
M 4 |s 4> |a 4> |b 4> |c 4> |S 4> 0 10 12 0 |A 4> 7 0 6 10 |B 4> 0 0 |C 4> 0 11 8 0

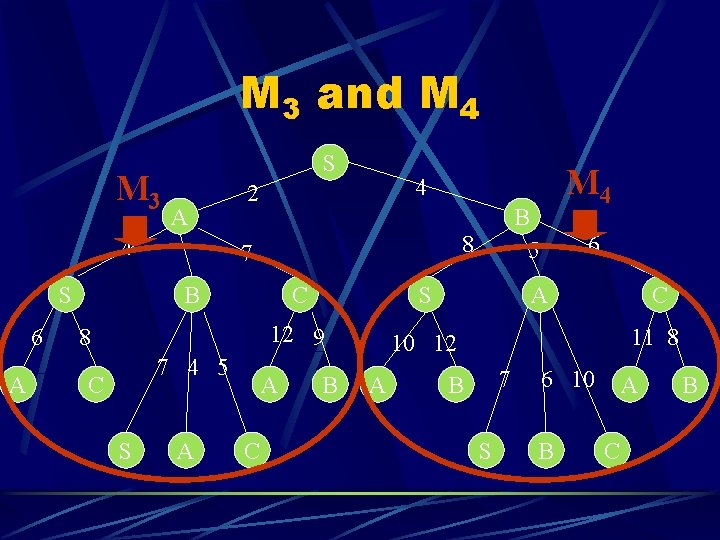
M 3 and M 4 They are each a separate side of the search tree M 3 is path from S down Node A l M 4 is path from S down Nobe B l

M 3 and M 4 Entry <Row|Column> is the distance from start to Row by path computed so far and then from row to column l Example: <B 3|s 3> in M 3 has the cumulative weight for S>A->B->S which is 7 l <B 4|s 4> in M 4 has the cumulative weight for S>B->B->S which is 0 l

M 3 and M 4 M 3 S A 4 S 6 A 8 7 4 5 C S A C S 12 9 10 12 A C B 5 8 7 B B M 4 4 2 A 6 A C 11 8 7 B S 6 10 B A C B

Step 3 Repeat step 2 adequate amount of times to reach bottom of tree and for each new matrix at each level

Step 4 Route exists if there is non zero value in a column Thus measure columns and non zero values are path

Expanding the Adjacency Matrix Creation Each row and column are a super position of quantum state vectors with N states where N is number of nodes The N states either show a weight if there is an edge or show that there is no weight ie the n states represent a weight

Issues Even if have weights, information on which node is connected to which is lost | s> = | s> + | a> + | b> + | c> looks okay but leads to: l |S 1> = a|000> + b|010> + c|100> + d|000> l

Issues Author calls for n distinct values but opens up problem of dealing with states that have the same weight Author agrees saying: l “There are problems describing the adjacency matrix as quantum state vectors”

Issues Algorithm calls for acting on single state in a superposition of states ie acting solely on state | a> for the vector | s> = | s> + | a> + | b> + | c>

Alternate Representation Add in qubits for the node in which this weight is for. One issue is make sure you have enough qubits to represent the weight l Furthermore the fact that the Qubits are no longer in a single state will complicate the QSUMAND l

Review Graph Basics Route Finding in general QAND The basic Algorithm Issues with Algorithm Fixes to be explored

Questions?

References Narayanan, A. , Wallace, J. , A Quantum Algorithm for Route Finding. Proceedings of the 15 th European Meeting on Cybernetics and Systems Research (EMCSR 2000), Vienna, Austria, 25 -28 April 2000, Vol. 1, pp 140 -143. Penrose, R. Shadows of the Mind: A search for the missing science of consciousness. Oxford University Press 1994. Shor, P. , Algorithms for quantum computation: Discrete logarithms and factoring 1994.

Follow Up I need a drink after all this.