Regresn a korelan analza Ra KA resp Korelan








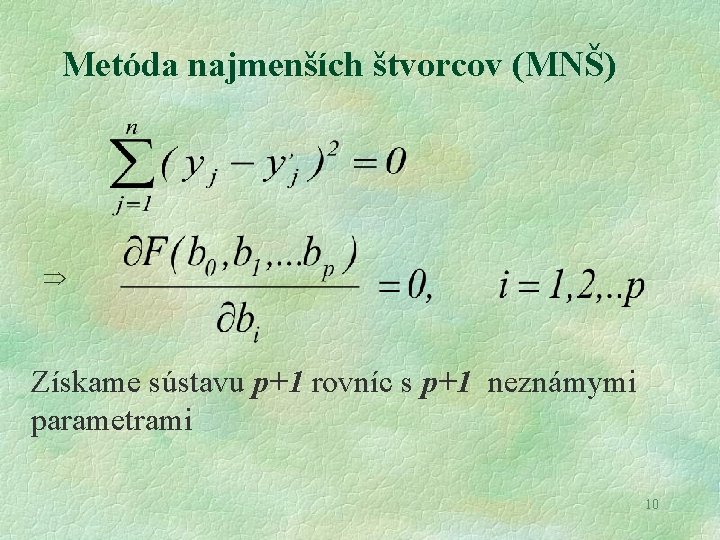
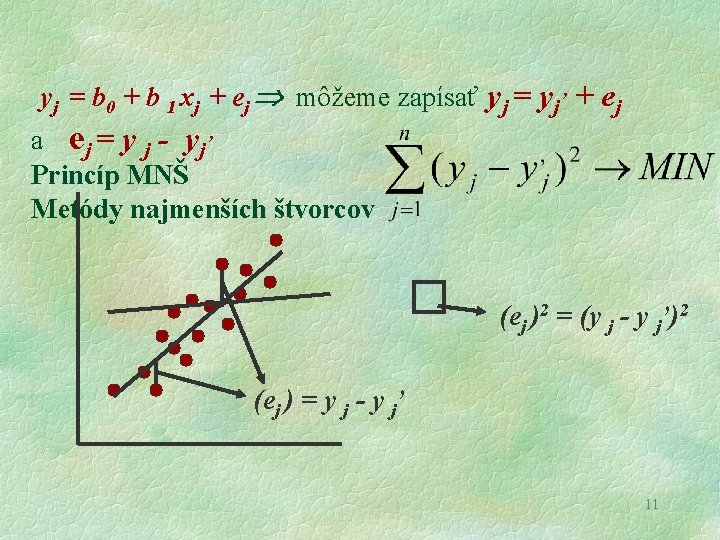







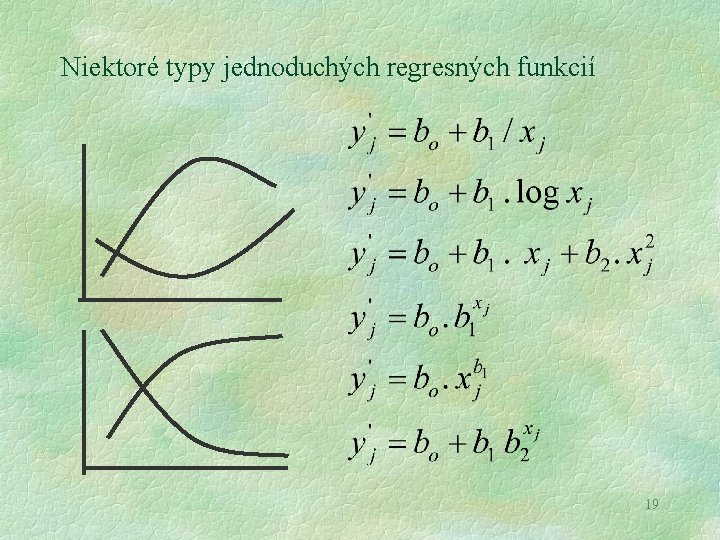









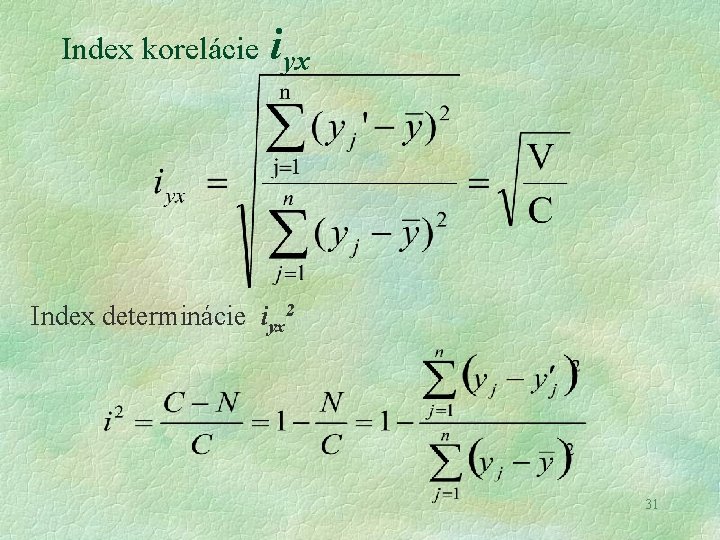









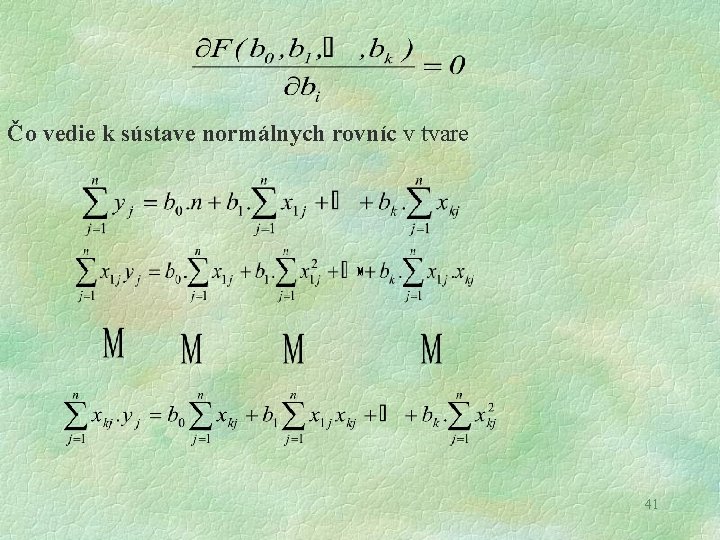



- Slides: 45

Regresná a korelačná analýza (Ra. KA) resp. Korelačný počet 1

Skúmanie vzťahov medzi štatistickými znakmi: § Skúmanie vzťahov medzi kvalitatívnymi znakmi, napr. A B , nazýme meranie asociácie § skúmanie vzťahov medzi kvantitatívnymi štatistickými znakmi - regresná a korelačná analýza 2

Pri regresenej a korelečnej analýze pôjde § skúmanie príčinnej - kauzálnej závislosti, skúmanie vzťahov medzi príčinou a účinkom § kedy jeden resp viac javov (znakov, nezávisle prememnných veličín ) vyvoláva účinok výsledný jav - závisle prememnnú veličinu Y = f (X 1 X 2…. . . Xk , Bo , B 1 , …. Bp ) +e Závislé premenná - účinok Nezávislé premenné veličiny - príčiny Neznáme parametre funkčného vzťahu Náhodné, nešpecifikované vplyvy 3

Príklady štatistickej - voľnej -závislosti § Skúmanie závislosti spotreby bravčového mäsa od príjmu, ceny mäsa bravčového ceny mäsa hovädzieho a hydiny a od tradície, resp. ďalších nešpecifikovaných, či náhodných vplyvov. § Skúmanie pridanej hodnoty resp. HNP od vstupov: práce a kapitálu…. § Skúmanie závislosti výživy obyvateľstva od stupňa ekonomického rozvoja krajiny…. 4

Opakom štatistickej závislosti je funkčná závislosť Y = f(X 1 X 2…. . . Xk , Bo , B 1 , …. , Bp) kedy je závisle prememnná veličina jednoznačne určená funkčným vzťahom, príklady z fyziky, chémie - takýto druh vzťahov nie je predmetom štatistického skúmania 5

Regresná a korelačná analýza (Ra. KA) § Dve základné úlohy Ra. KA: regresná úloha (RÚ) jej podstatou je a) nájsť funkčný vzťah podľa ktorého sa mení závislé premenná so zmenou nezávisle premenných - nájsť vhodnú regresnú funkciu. b) Súčasne je potrebné odhadnúť parametre regresnej funkcie. l korelačná úloha (KÚ)- merať tesnosť - silu skúmanej závislosti. l 6

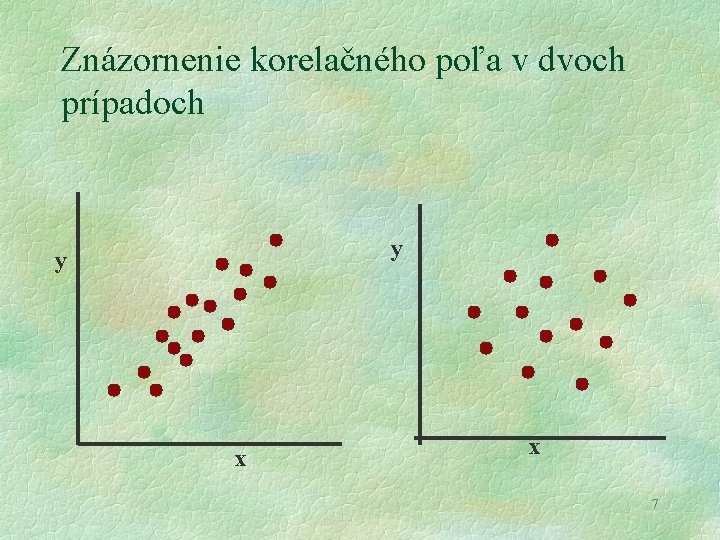
Znázornenie korelačného poľa v dvoch prípadoch y y x x 7

Podľa počtu nezávisle premenných rozlišujeme: § Jednoduchú závislosť , kedy uvažujeme len jednú nezávislé premennú X, teda skúmame vzťah medzi Y a X § viacnásobnú závislosť, pri ktorej uvažujeme minimálne dve nezávislé prememnné veličiny (znaky) X 1, X 2, … Xk , pričom k 2 8

Jednoduchá regresná a korelačná analýza § Uvažujme štatistický znak X a Y medzi ktorými je v základnom súbore lineárna závislosť Y = Bo + B 1 X +e bodovým odhadom tejto regresnej funkcie je priamka yj = b 0 + b 1 xj + ej , ktorej koeficienty vypočítame z výberových údajov Akú metódu použiť ? ? ? 9
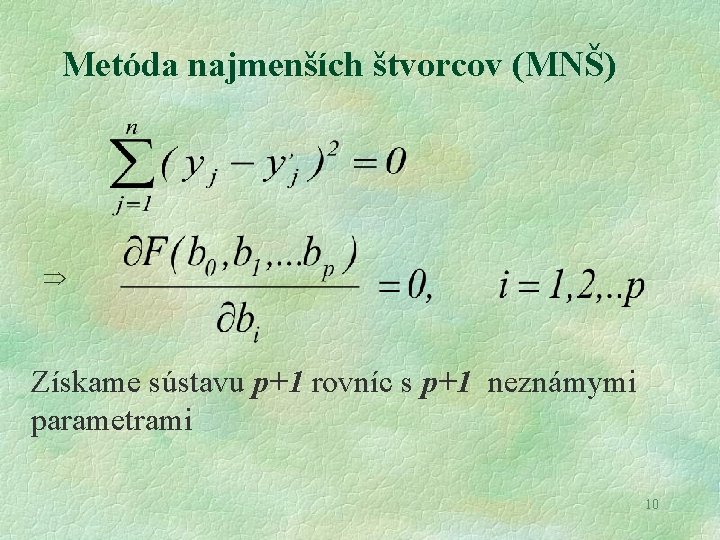
Metóda najmenších štvorcov (MNŠ) Získame sústavu p+1 rovníc s p+1 neznámymi parametrami 10
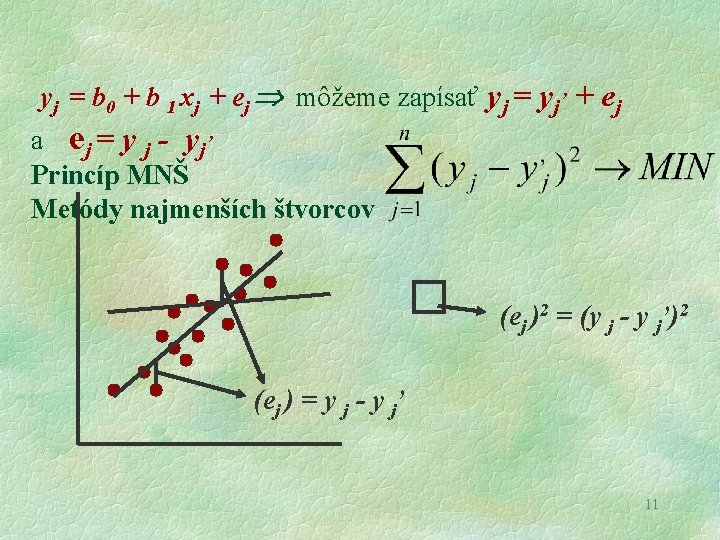
yj = b 0 + b 1 xj + ej môžeme zapísať yj = yj , + ej a ej = y j - yj , Princíp MNŠ Metódy najmenších štvorcov (ej )2 = (y j - y j’)2 (ej ) = y j - y j’ 11

Možno dokázať, že koeficienty bo , b 1 , …, bp určené MNŠ sú “najlepšie odhady” parametrov B 0 , B 1 , …, Bp ak súčasne o náhodných chybách platí: § E (ej ) = 0, § D (ej ) = E (ej 2 ) = 2 , § E(ej 1 , ej 2 ) = 0 , pre každé j 1 j 2 Slovne možno podmienku formulovať nasledovne: od náhodných chýb požadujeme nulovú strednú hodnotu, konštantný rozptyl a vzájomnú nezávislosť náhodných chýb. 12

Koeficienty jednoduchej regresnej funkcie odvodíme: 13

Úpravou získame nasledovné dve normálové rovnice s dvomi neznámymi parametrami: Sústavu rovníc môžme riešiť eliminačnou metódou , alebo pomocou determinantov. Získame tak koeficienty b o a b 1 14

Postup pri výpočte koeficientov LRF xj yj xj 2 x 1 y 1 x 12 x 2 y 2 xn yn 15

Interpretácia koeficientov ljednoduchej lineárnej regresnej funkcie § bo …lokujúca konštanta vyjadruje očakávanú úroveň závislé premennej pri nulovej hodnote nezávisle premennej § b 1 …. regresný koeficient vyjadruje o koľko merných jednotiek sa zmení závislé premenná pri zmene nezávisle premennej o jednu mernú jednotku § ak b 1 > 0 …ide o pozitívnu závislosť § po b 1< 0 …. jedná sa o negatívnu závislosť 16

Vlastnosti metódy najmenších štvorcov: Regresná funkcia prechádza bodom o súradniciach a 17

Kedy možno MNŠ aplikovať? § Ak je regresná funkcia lineárna § lineárna v parametroch (Lv. P) § alebo vieme regresnú funkciu transformovať na lineárnu v prametroch § Posúďte u ktorých z nasledujúccich § regresných funkcií možno použiť MNŠ 18
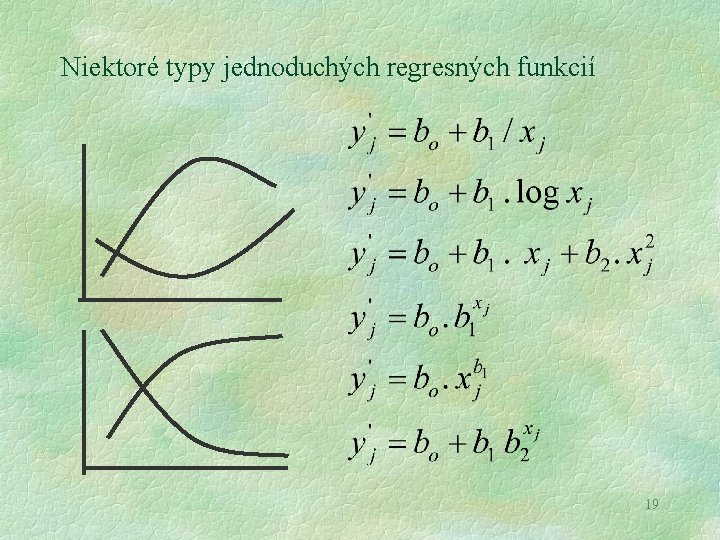
Niektoré typy jednoduchých regresných funkcií 19

Nelineárna regresná a korelačná analýza Okrem lineárnych regresných funkcií sa v praxi veľmi často používa celý rad nelineárnych funkcií, pričom je možné použiť nelineárne funkcie s dvoma alebo viacerými parametrami. Niektoré nelineárne regresné funkcie je možné vhodnou transformáciou upraviť na lineárne v parametroch, ktoré potom môžeme riešiť metódou najmenších štvorcov. Najčastejšie môžeme nelineárne funkcie s dvoma parametrami transformovať na tvar: 20

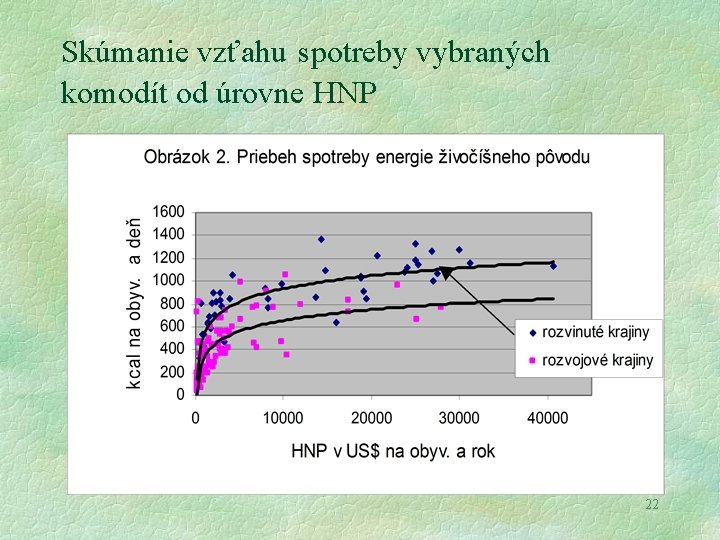
Príklady z mikro- a makroekonómie § § § Philipsova krivka ? ? Cobbova -Douglasova produkčná funkcia Engelove krivky Krivky ekonomického rastu Uveďte ďalšie…. . . 21

Skúmanie vzťahu spotreby vybraných komodít od úrovne HNP 22

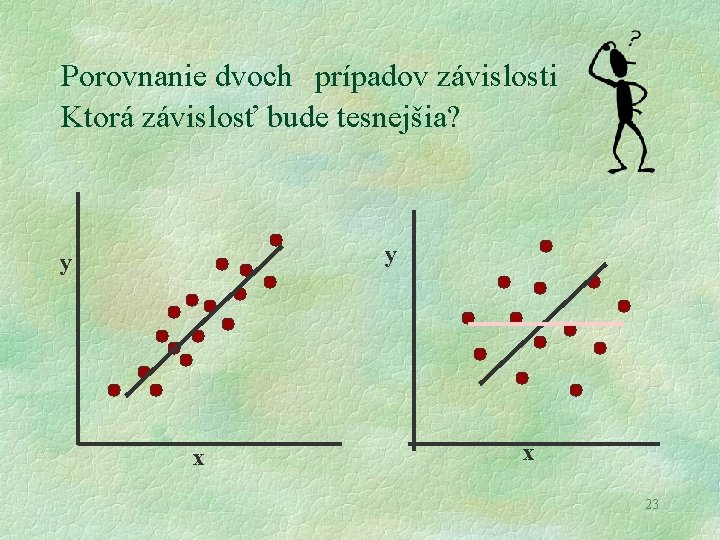
Porovnanie dvoch prípadov závislosti Ktorá závislosť bude tesnejšia? y y x x 23

Intervaly spoľahlivosti pri lineárnej regresii. Okrem bodových odhadov parametrov lineárnej regresnej funkcie sa často prepočítavajú aj intervalové odhady parametrov, ktoré nazývame intervaly spoľahlivosti. Výpočty intervalov spoľahlivosti je možné urobiť s pomocou štandardných odchýlok parametrov a reziduálneho rozptylu. Reziduálny rozptyl je za predpokladu platnosti podmienok lineárneho klasického modelu , neskresleným odhadom stochastického parametra a vypočíta sa podľa vzťahu 24

kde je reziduálny rozptyl a je i - ty diagonálny prvok momentovej matice M-1 = (XTX)-1 pre priamku, tj. M-1 = 25

Intervalový odhad ľubovoľného parametra pre regresnú priamku vychádza z toho, že za predpokladov formulovaných klasickým lineárnym modelom má veličina t rozdelenie s n – p stupňami voľnosti. Pri zvolenej spoľahlivosti 1 – je obojstranný interval spoľahlivosti pre parameter daný vzťahom 26

a pre parameter analogicky sa konštruuje aj obojstranný interval spoľahlivosti pre regresnú priamku kde je kvantil t rozdelenia s (pre regresnú priamku n – 2) stupňami voľnosti. 27

Korelačná úloha korelačného počtu § Skúmať tesnosť - silu - závislosti § k tomu slúžia miery tesnosti závislosti § požadujeme, aby sa pohybovali v pevne ohraničanom intervale, § a aby vrámci intervalu rástli s vyššiou silou závislosti 28

Korelačná analýza predstavuje súhrn metód a postupov, pomocou ktorých overujeme vypovedaciu schopnosť kvantifikovaných regresných modelov ako celku aj jeho častí. Overovanie vypovedacej schopnosti kvantifikovaných regresných modelov vedie k výpočtu číselných charakteristík, ktoré v koncentrovanej forme popisujú kvalitu vypočítaných modelov. 29

Index korelácie a index determinácie V základnom súbore Iyx odhadom z výberových údajov je iyx est Iyx = iyx. Princíp spočíva v rozklade variability závisle premennne Y Celková variabilita závisle premennej Variabilita závisle premennej vysvetlená regresnou funkciou Variabilita nevysvetlená regresnou funkciou - reziduálna variabilita 30
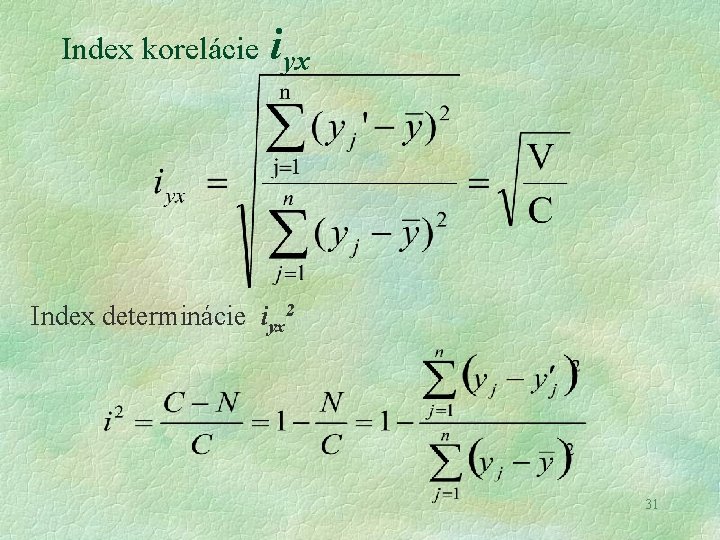
Index korelácie iyx Index determinácie iyx 2 31

Index determinácie môže nadobúdať hodnoty z intervalu 0 až 1 , čím viac sa hodnota indexu blíži k jednotke, tým väčšia časť celkovej variability je modelom vysvetlená a naopak, ak sa index determinácie blíži k nule, tým menšia časť celkovej variability je modelom vysvetlená. Index determinácie sa bežne používa ako kritérium pri rozhodovaní o voľbe konkrétneho tvaru regresnej funkcie. Ak však majú regresné funkcie rôzny počet parametrov je potrebné upraviť index determinácie do korigovanej podoby v tvare: 32

Variabilita Vysvetlená Súčet štvorcov odchýlok Stupne voľnosti Rozptyl F test V= F= Nevysvetlená N= Celková C= 33

. Je zrejmé, že platí vzťah C=V+N C= je celkový súčet štvorcov odchýlok V= je vysvetlený súčet štvorcov odchýlok N= je nevysvetlený (reziduálny) súčet štvorcov odchýlok. 34

Testovacie kritérium v tabuľke je možné využiť k súčasnému testovaniu významnosti celého regresného modelu, indexu determinácie aj indexu korelácie. Vypočítanú hodnotu F testu porovnávame s kvantilom F rozdelenia a p-1 a n – p stupňov voľnosti tj. ak F považujeme regresný model za nevýznamný, podobne aj index determinácie a index korelácie. ak F > považujeme regresný model za štatisticky významný, podobne aj index determinácie a index korelácie 35

K detailnému vyhodnoteniu kvality jednotlivých parametrov regresného modelu sa používajú t testy parametrov. Pri teste formulujeme nulovú hypotézu H 0 : pre i = 0, 1 H 1 : v ktorej predpokladáme nulové teda nevýznamné pôsobenie či vplyv premennej pri ktorej parameter stojí. Testovacie kritérium je definované vzťahom 36

kde a je hodnota parametra regresnej funkcie je štandardná odchýlka parametra. Vypočítanú hodnotu testovacieho kritéria porovnávame s kvantilom t rozdelenia na hladine významnosti a stupňov voľnosti tj. : - ak nulovúhypotézu o nevýznamnosti parametra nezamietame - ak zamietame nulovú hypotézu a potvrdzujeme štatistickú významnosť posudzovaného parametra. 37

Je potrebné si uvedomiť, že transformované regresné funkcie nemajú vždy rovnaké parametre ako pôvodné nelineárne regresné funkcie, takže je potrebné z odhadnutých parametrov transformovaných regresných funkcií spätne prepočítať odhady pôvodných parametrov. Takto získané odhady pôvodných parametrov síce nemajú optimálne štatistické vlastnosti, ale pre riešenie konkrétnych úloh často postačujú. Niektoré regresné funkcie nie je možné ani transformáciou premenných upraviť na funkcie lineárne v parametroch. Odhady parametrov takýchto funkcií sa získavajú pomocou rôznych aproximatívnych iteračných metód. Väčšina z nich je založená na postupnom zlepšovaní tzv. prvotných odhadov, ktorými môžu byť napríklad expertné odhady, odhady získané metódou vybraných bodov a pod. 38

Viacnásobná regresná a korelačná analýza Predpokladajme, že medzi závisle premennou Y a vysvetľujúcimi (nezávisle) premennými Xi , i = 1, 2, . . . , k je lineárna závislosť, o ktorej sme sa už z časti zmienili v predchádzajúcich častiach popísaná rovnicou ktorú odhadneme rovnicou 39

keďže predpokladáme konkrétny tvar regresnej funkcie môžeme ho dosadiť do predchádzajúceho vzťahu a hľadať minimum tejto funkcie tj. : minimum funkcie určíme podobne ako pre prípad jednoduchej regresnej závislosti pomocou parciálnych derivácií funkcie 40
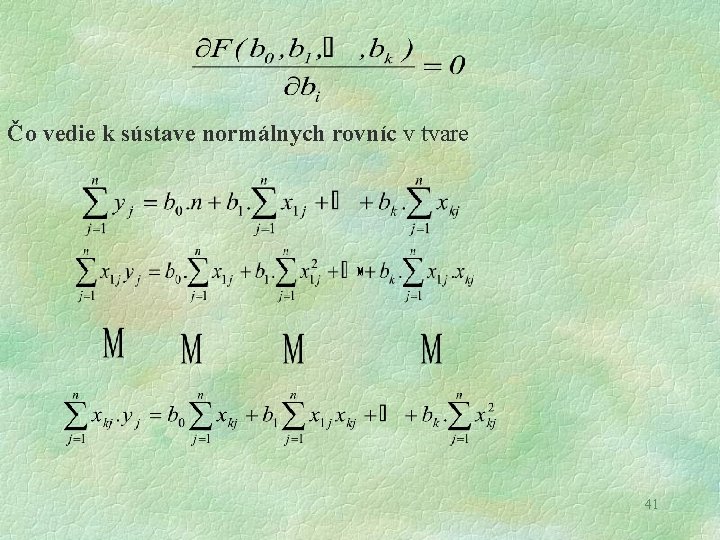
Čo vedie k sústave normálnych rovníc v tvare 41

Riešením tejto sústavy rovníc vypočítame hľadané koeficienty lineárnej regresnej rovnice Podobne ako pre jednoduchú lineárnu závislosť, môžeme odhad parametrov vypočítať z maticovej rovnice Kvalitu regresného modelu hodnotíme podobne ako pre jednoduchú 42 lineárnu závislosť, ktorú sme popísali v predchádzajúcej časti

43

44

45
 Korelan
Korelan Korelan
Korelan Resp
Resp Acute resp acidosis
Acute resp acidosis Resp
Resp Cell resp equation
Cell resp equation Ia resp diploma plan
Ia resp diploma plan Ia diploma resp
Ia diploma resp Types of respiratory failure
Types of respiratory failure Swot analysis objectives
Swot analysis objectives Entitno-relačný model databázy
Entitno-relačný model databázy Analuza
Analuza Analza
Analza Ssreg
Ssreg Analza
Analza Analzy
Analzy Analzy
Analzy Cobb douglasova produkční funkce
Cobb douglasova produkční funkce Post hoc definition
Post hoc definition Analze
Analze Analzy
Analzy Analza
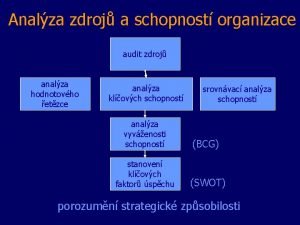
Analza Swot analza
Swot analza Analza
Analza Analza
Analza Swot analza
Swot analza Swot analza
Swot analza Cronbachova alfa výpočet
Cronbachova alfa výpočet Zlate bilancne pravidlo
Zlate bilancne pravidlo Swot analza
Swot analza Swot analza
Swot analza úsečkový diagram
úsečkový diagram Analza
Analza Suroviny
Suroviny Analza
Analza Analza
Analza