Regresi Linier Berganda Diah Indriani Bagian Biostatistika dan

Regresi Linier Berganda Diah Indriani Bagian Biostatistika dan Kependudukan Fakultas Kesehatan Masyarakat Universitas Airlangga 1

Regresi Linier Berganda Model regresi linier berganda melibatkan lebih dari satu variabel bebas. Modelnya : Dimana Y = variabel terikat Xi = variabel bebas ( i = 1, 2, 3, …, k) 0 = intersep i = koefisien regresi ( i = 1, 2, 3, …, k) Model penduganya adalah 2

Regresi Linier Berganda Misalkan model regresi dengan kasus 2 variabel bebas X 1 dan X 2 maka modelnya : Sehingga setiap pengamatan Akan memenuhi persamaan 3

Menaksir Koefisien Regresi Dengan Menggunakan Matriks Dari hasil Metode Kuadrat Terkecil didapatkan persamaan normal : …. . 4

Menaksir Koefisien Regresi Dengan Menggunakan Matriks Tahapan perhitungan dengan matriks : 1. Membentuk matriks A, b dan g 5

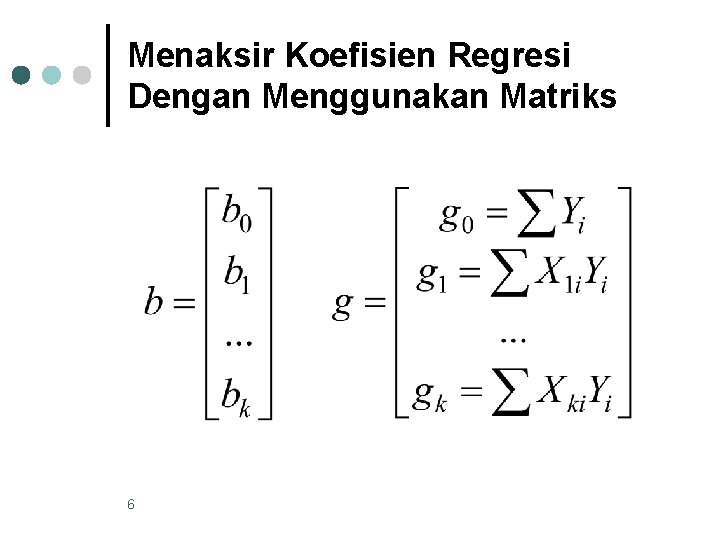
Menaksir Koefisien Regresi Dengan Menggunakan Matriks 6

Menaksir Koefisien Regresi Dengan Menggunakan Matriks 2. Membentuk persamaan normal dalam bentuk matriks Ab=g 3. Perhitungan matriks koefisien b b = A-1 g 7

Metode Pendugaan Parameter Regresi Dengan Metode Kuadrat Terkecil, misalkan model terdiri dari 2 variabel bebas Tahapan pendugaannya : 1. Dilakukan turunan pertama terhadap b 0 , b 1 dan b 2 8

Metode Pendugaan Parameter Regresi 2. Ketiga persamaan hasil penurunan disamakan dengan nol 9

Metode Pendugaan Parameter Regresi 3. Nilai b 1 dan b 2 dapat diperoleh dengan memakai aturan-aturan dalam matriks 10

Uji Kecocokan Model 1. Dengan Koefisien Determinasi R 2 menunjukkan proporsi variasi total dalam respon Y yang dapat diterangkan oleh model r merupakan koefisien korelasi antara Y dengan kelompok X 1 , X 2 , X 3 , … , Xk 11

Uji Kecocokan Model Dengan Pendekatan Analisis Ragam Tahapan Ujinya : 1. Hipotesis = H 0 : 0 H 1 : 0 dimana = matriks [ 0, 1, 2, … , k ] 2. 12

Uji Kecocokan Model 2. Tabel Analisis Ragam Komponen Regresi SS db MS Fhitung Regresi SSR k MSR=SSR / k MSR s 2 Eror SSE n – k – 1 s 2 = SSE / n-k-1 Total SST 13 n– 1

Uji Kecocokan Model Dimana : 14

Uji Kecocokan Model 3. Pengambilan Keputusan H 0 ditolak jika Fhitung > Ftabel(k , n-k-1) pada taraf kepercayaan 15

Uji Parsial Koefisien Regresi Tahapan Ujinya : 1. Hipotesis = H 0 : j 0 H 1 : j 0 dimana j merupakan koefisien yang akan diuji 16

Uji Parsial Koefisien Regresi 2. Statistik uji : Dimana : bj = nilai koefisien bj s= 17

Uji Parsial Koefisien Regresi 3. Pengambilan keputusan H 0 ditolak jika thitung > t /2(db= n-k-1) pada taraf kepercayaan 18