REGRESI LINIER BERGANDA Model Regresi Berganda Bentuk umum

REGRESI LINIER BERGANDA

Model Regresi Berganda Bentuk umum model regresi dengan k peubah bebas adalah sebagai berikut: merupakan koefisien regresi yang harus diduga.

Asumsi-Asumsi • Eksistensi Untuk setiap nilai X 1, X 2, …, Xk tertentu, Y merupakan peubah acak dengan sebaran probabilitas tertentu yang memiliki nilai tengah dan ragam • Saling bebas Nilai-nilai Y saling bebas satu sama lain secara statistik • Ke-linier-an Nilai tengah Y, merupakan fungsi linier dari X 1, X 2, …, Xk

Pendugaan Parameter Beberapa metode pendugaan parameter: 1. Metode Kuadrat Terkecil(MKT) 2. Metode Ragam Minimum Menentukan nilai dugaan parameter dengan ragam terkecil sebagai penduga tak bias.

Analisis Ragam Sumber Keragaman Derajat Bebas (db) Jumlah Kuadrat (JK) Kuadrat F-hitung Tengah (KT) Regresi k JKR/k Sisaan n-k-1 JKS/n-k-1 Total n-1 KTR/KTS
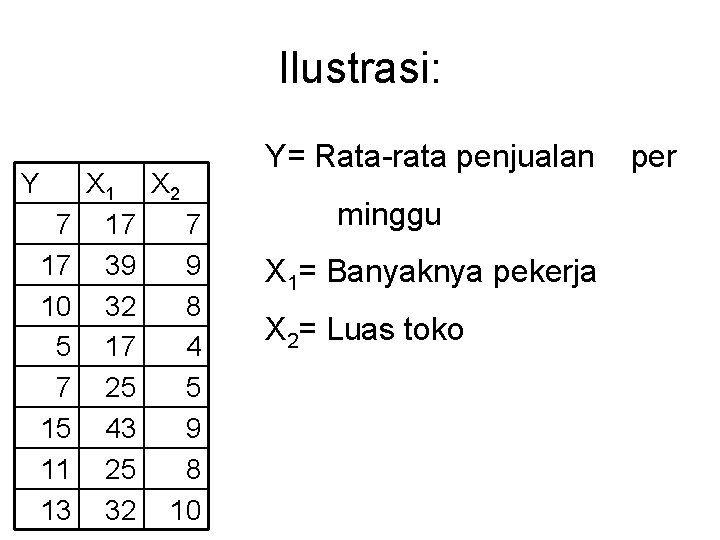
Ilustrasi: Y 7 17 10 5 7 15 11 13 X 1 X 2 17 7 39 9 32 8 17 4 25 5 43 9 25 8 32 10 Y= Rata-rata penjualan minggu X 1= Banyaknya pekerja X 2= Luas toko per
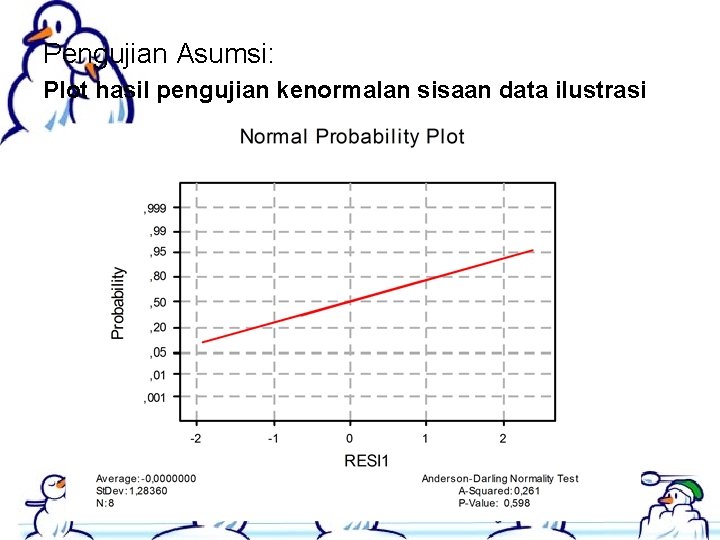
Pengujian Asumsi: Plot hasil pengujian kenormalan sisaan data ilustrasi

Plot sisaan dengan dugaan respon data ilustrasi

Plot sisaan dengan urutannya pada data ilustrasi

Model Regresinya: Y = - 3, 42 + 0, 264 X 1 + 0, 861 X 2 R 2= 90, 7% Analisis Ragam Sumber Regresi Sisaan Total DF 2 5 7 SS 112, 342 11, 533 123, 875 MS 56, 171 2, 307 F 24, 35 -
- Slides: 10