ANALISIS REGRESI GANDA LOGISTIK Multiple Regression Logistic Pengertian

ANALISIS REGRESI GANDA LOGISTIK Multiple Regression Logistic

Pengertian Regresi Logistik: �Suatu model matematik yang digunakan untuk mempelajari hubungan satu atau beberapa variabel independen dengan satu variabel dependen yang bersifat dikotomi (binary). Variabel bianry : adalah variabel yang hanya memiliki dua nilai, misalnya (sakit / sehat), (merokok/ tdk merokok), (BBLR/ normal) dll �Variabel Independen (prediktor) sebaiknya kategorik, agar mudah untuk menginterpretasikan hasil analisisnya. �Bila variabel prediktor 3 kategori atau lebih, maka dibuat dua kategori. Caranya ; dummy variabel, kategori ulang sesuai logika biologik.

Pengertian Regresi Logistik. . . . �Analisis regresi ganda logistik adalah alat statistik yang sangat kuat untuk menganalisis hubungan antara paparan dan penyakit dengan serentak mengontrol pengaruh sejumlah faktor perancu potensial. �Tujuan analisis regresi ganda logistik yaitu menemukan model regresi yang paling sesuai, paling irit, sekaligus masuk akal secara biologik, untuk menggambarkan hubungan antara variabel dependen dan satu set variabel prediktor dalam populasi. �Manfaat analisis regresi ganda : (a) Meramalkan terjadinya variabel dependen pada individu berdasarkan nilai-nilai sejumlah variabel prediktor

Pengertian Regresi Logistik. . . . �Manfaat : (b) Mengukur hubungan antara veriabel respon dan prediktor, setelah mengontrol pengaruh prediktor (kovariat) lainnya.

Keistimewaan Regresi Logistik Ganda (a) Kemampuan kengkonversi koefisien regresi (bi) menjadi rasio odds (OR). OR = exp [bi] (b) Kemampuan menaksir probabilitas individu untuk sakit (mengalami event) berdasarkan nilai -nilai sejumlah variabel prediktor, dengan rumus sebagai berikut :

Macam Regresi logistik : 1. Regresi logistik sederhana Untuk mempelajari hubungan antara satu variabel prediktor dengan satu variabel dependen dikotomus. 2. Regresi logistik ganda (Multiple Regression Logistic) Untuk mempelajari hubungan antara beberapa variabel prediktor dengan satu varibel dependen dikotomus.

Model Regresi Ganda Logistik Ln (p/(1 -p) = logodd (logit). Logaritme natural dari odds. Odds : rasio probabilitas suatu peristiwa untuk terjadi dan probabilitas suatu peristiwa untuk tidak terjadi a = Konstanta ( intersep) b 1 , b 2 , . . bk = koefisien regresi variabel prediktor (slope) X 1, X 2. . Xk = variabel prediktor yg pengaruhnya akan diteliti.

Membangun Model Regresi Ganda Logistik �Pembangunan model regresi ganda logistik hendaknya tidak terjebak oleh penggunaan veriabel prediktor yang terlalu banyak. �Pemilihan variabel sebaiknya dilakukan dengan cara-cara yang lebih purposif, dan tidak terpaku pada pendekatan yang sifatnya deterministik menurut kamaknaan statistik.

MEMBANGUN MODEL REGRESI GANDA LOGISTIK. . . �Makin banyak variabel yang dimasukkan dalam model hanya akan meningfkatkan kesesuaian garis regresi dengan hubungan antara variabel dependen dan sejumpan variabel prediktor pada data sampel, tetapi belum tentu menggambarkan hubungan tersebut pada tingkat populasi. �Hal itu disebabkan karena, bertambahnya variabel prediktor (baik yang relevan maupun tidak relevan) hanya akan menaikkan nilai taksiran kesalahan baku, sehingga membuat model tersebut sangat tegantung kepada data pengamatan sampel. �Kesimpulannya, model tersebut tidak merefleksikan / meggambarkan hubungan

PROSEDUR PEMILIHAN VARIABEL Agar diperoleh model regresi yang baik adalah sebagai berikut : 1. Melakukan analisis univariate untuk menyaring variabel-variabel yang penting. 2. Memasukkan dan/ atau mengeluarkan variabel dalam model multivariate 3. Memasukkan dan memeriksa kemungkinan ada interaksi variabel dalam model.

Melakukan analisis univariate untuk penyaringan awal : Uji statistik yang dipakai adalah : chi-quadrat q Jika ada variabel prediktor lebih dari dua kategori, maka dibuat menjadi dua kategori terlebih dahulu. Perlu diingat bahwa dalam melakukan recode harus mempunyai alasan biologik. q Mickey dan Greenland : variabel yang mempunyai nilai p= 0, 25 dan memiliki kemaknaan biologik hendaknya dipertimbangkan untuk dimasukkan ke dalam model multivariate. q

Univariate. . . . �Batasan P= 0, 25, untuk mengantisipasi kemungkinan variabel yang secara terselubung sesungguhnya penting untuk dimasukkan dalam model. “Terselubung” kemungkinan variabel secara kolektif dapat menjadi prediktor penting, walaupun secara sendiri merupakan prediktor lemah.

Memasukkan / mengeluarkan variabel dalam model regresi : Beberapa Metode : 1. Enter 2. Stepwise 3. Forward 4. Backward Conditional, LR (likelihood ratio), Wald

Memeriksa Kemungkinan Interaksi �Jika dengan uji interaksi menunjukkan kemaknaan statistik, maka kita katakan interaksi memberikan kontribusi penting kepada model. Jika suatu interaksi hanya memperbesar taksiran kesalahan baku (S. E. ) dan tidak mengubah taksiran koefisiens regresi (b 1), maka interaksi tersebut mungkin tidak penting. �

Latihan Sebuah studi Kohor prospektif, meneliti pengaruh aktifitas fisik (AF) terhadap kejadian infark otot jantung (MI). Variabel lain yang diukur adalah umur dalam kategori (AGRP) dan kebiasaan merokok.

Kategorisasi nilai variabel MI AF AGRP = 1 : sakit 0 : tidak sakit = 1 : aktifitas fisik >= 2500 kcal/ hari 0 : aktifitas fisik < 2500 kcal/hari = 1 : umur >= 55 tahun 0 : umur < 55 tahun Kebiasaan merokok hari = 2 : merokok >= 15 btg / 1 : merokok < 15 btg /hari 0 : tidak merokok

Varabel rancangan Kebiasaan merokok - Jumlah variabel yang dibutuhkan ( k-1) 3 -1 : 2 - Sebagai contoh MRK menjadi D 1 dan D 2 - Sebagai salah satu rancangan pengkodean variabel tersebut, maka variabel bukan perokok sebagai variabel acuan (refference) dengan kode D 1=0 D 2=0 - Selanjutnya merokok <15 btg / hari D 1=1 D 2=0 - Dan merokok >= 15 btg/hari D 1=0 D 2=1

Sehingga menjadi : Variabel asli rancangan MRK Tidak merokok Merokok < 15 btg / hari Merokok >= 15 btg / hari Variabel D 1 D 2 1 0 0 0 1 0 File download : http: //www. ziddu. com/download/8461706/Regresi. Logistik. ra r. html

Cek kelayakan variabel untuk dimasukkan dalam model : Menggunakan chi-square Kriteria variabel yang masuk p=0, 25

Hasil analisis univariate. . . ? AF AGRP D 1 D 2 p=0, 000 p=0, 052

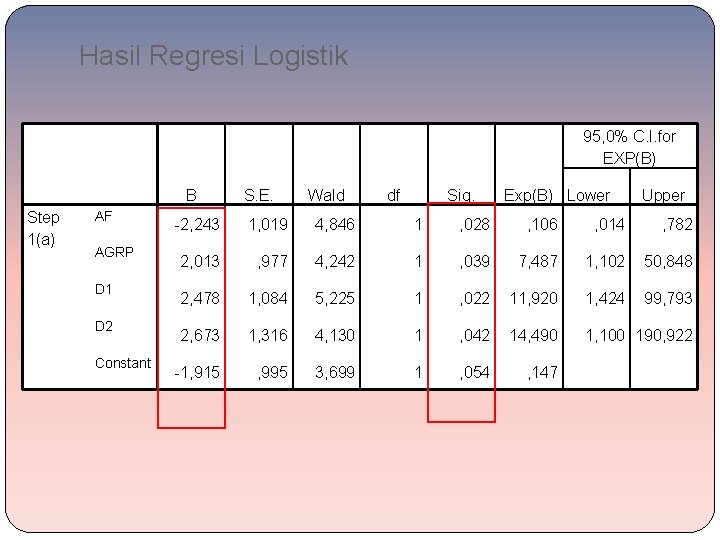
Hasil Regresi Logistik 95, 0% C. I. for EXP(B) B Step 1(a) AF AGRP D 1 D 2 Constant S. E. Wald df Sig. Exp(B) Lower Upper -2, 243 1, 019 4, 846 1 , 028 , 106 , 014 , 782 2, 013 , 977 4, 242 1 , 039 7, 487 1, 102 50, 848 2, 478 1, 084 5, 225 1 , 022 11, 920 1, 424 99, 793 2, 673 1, 316 4, 130 1 , 042 14, 490 1, 100 190, 922 -1, 915 , 995 3, 699 1 , 054 , 147

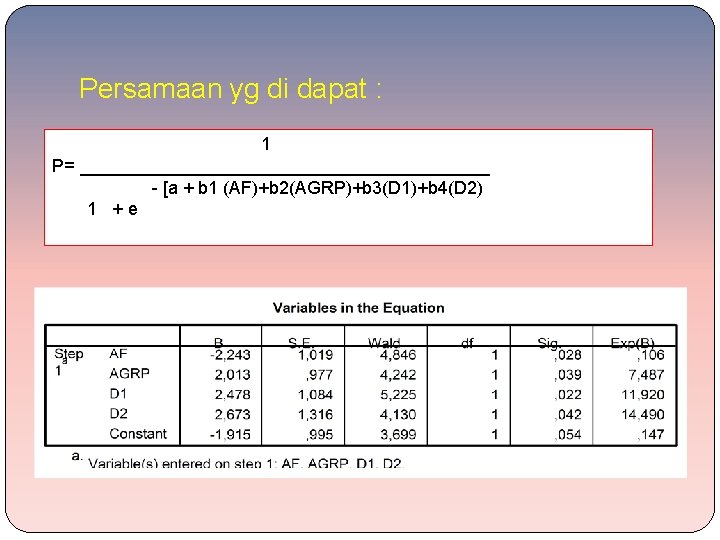
Persamaan yg di dapat : 1 P= _____________________ - [a + b 1 (AF)+b 2(AGRP)+b 3(D 1)+b 4(D 2) 1 +e

Meramalkan Probabilitas Individu untuk mengalami sakit Berdasarkan persamaan tersebut diatas, berapa probabilitas untuk mengalami sakit pada individu dengan kriteria sebagai berikut ? 1) Melakukan aktifitas fisik 2. 000 kcal / hari 2) Berumur 35 tahun 3) Merokok rata-rata 5 btg / hari

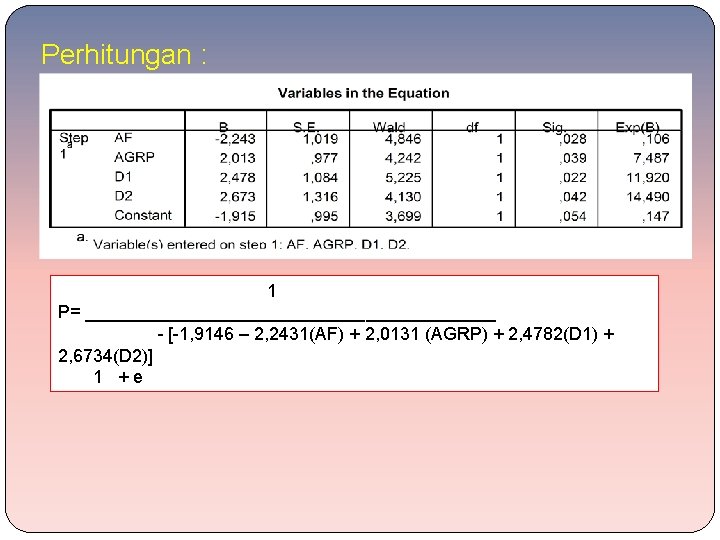
Perhitungan : 1 P= _____________________ - [-1, 9146 – 2, 2431(AF) + 2, 0131 (AGRP) + 2, 4782(D 1) + 2, 6734(D 2)] 1 +e

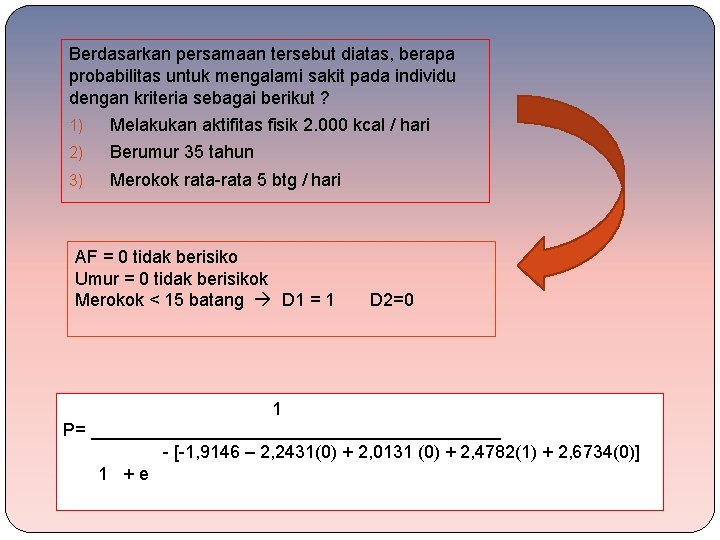
Berdasarkan persamaan tersebut diatas, berapa probabilitas untuk mengalami sakit pada individu dengan kriteria sebagai berikut ? 1) Melakukan aktifitas fisik 2. 000 kcal / hari 2) Berumur 35 tahun 3) Merokok rata-rata 5 btg / hari AF = 0 tidak berisiko Umur = 0 tidak berisikok Merokok < 15 batang D 1 = 1 D 2=0 1 P= _____________________ - [-1, 9146 – 2, 2431(0) + 2, 0131 (0) + 2, 4782(1) + 2, 6734(0)] 1 +e

Perhitungan : 1 P= _____________________ - [-1, 9146 – 2, 2431(0) + 2, 0131 (0) + 2, 4782(1) + 2, 6734(0)] 1 +e = 0, 64 64% In mathematics, the exponential function is the function ex, where e is the number (approximately 2. 71828)

Interpretasi : Individu yang berumur 35 tahun dan hanya melakukan aktifitas fisik sebesar 2. 000 kcal / hari, serta membunyai kebiasaan merokok 5 batang per hari, maka memiliki probabilitas untuk terkena MI sebesar 64%.

TERIMAKAS IH

Interaksi Asumsi adanya Interaksi 1. Logika substantif / biologik 2. Interaksi antara variabel a dan b, terjadi bila efek a terhadap Y tergantung nilai b, atau efek b terhadap Y tergantung nilai a.