Recursive Definitions and Induction Proofs Rosen 3 4

Recursive Definitions and Induction Proofs Rosen 3. 4

More Fibonacci Numbers Prove for n 2 Basis step, for n=2 ,

More Fibonacci Numbers Inductive Step Assume for 2 k n Show ,

More Fibonacci Numbers

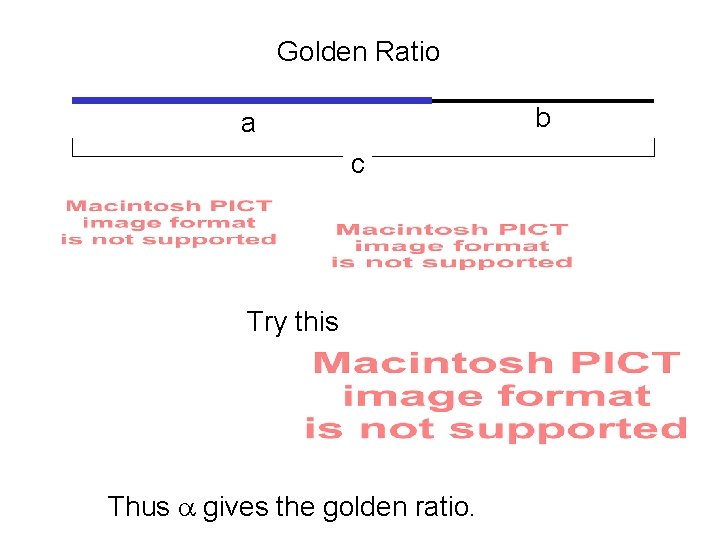
More Fibonacci Numbers But we showed before that if then = (1+ 5)/2. More generally, = (1+ 5)/2 b= (1 - 5)/2 and is the golden ratio (often labeled f)! ,

Golden Ratio b a c Try this Thus gives the golden ratio.

Golden Ratio What is fn+1/ fn as n gets very large? Recall fn+1/ fn approaches the golden ratio ( ) as n gets very large! = (1+ 5)/2 b = (1 - 5)/2 What happens to n and bn as n gets very large?

Prove that the function g(n) = f 1 + f 3 + … + f 2 n-1 (where fi is a Fibonacci number) is equal to f 2 n whenever n is a positive integer. Basis Step If n = 1, then g(1) = f 2*1 - 1 = f 2 Inductive Step Assume g(k) = f 1 + f 3 + … + f 2 k-1 = f 2 k for k n, we must show that this implies g(n+1) = f 2(n+1) g(n+1) = f 1 + f 3 + … + f 2 n-1 + f 2 n+1 g(n+1) = g(n) + f 2 n+1 g(n+1) = f 2 n + f 2 n+1 = f 2 n+2 = f 2(n+1)

Find a closed form solution for the recursive definition: T(n) = T(n/2) + c 1, T(1) = c 0 where n is 2 k for k N. T(1) = c 0 T(2) = T(1) + c 1 = c 0 + c 1 T(4) = T(2) + c 1 = c 0 + 2 c 1 T(8) = T(4) + c 1 = c 0 + 2 c 1 = c 0 + 3 c 1 T(16) = T(8) + c 1 = c 0 + 3 c 1 + c 1 = c 0 + 4 c 1 Guess that T(n) = c 0 + c 1 log 2 n

Proof of guess Proof by Induction. Basis Step: T(1) = c 0 + c 1 log 21 = c 0 + c 1*0 = c 0 Inductive Step: Assume that T(n) = c 0 + log 2 nc 1, then we must show that T(2 n) = c 0 + c 1 log 2(2 n). T(2 n) = T(n) + c 1 = c 0 + c 1 log 2 n + c 1 log 22 = c 0 + c 1(log 2 n + log 22) = c 0 + c 1 log 2(2 n)

Ackermann’s Function A(m, n) = 2 n if m = 0 0 if m 1 and n = 0 2 if m 1 and n = 1 A(m-1, A(m, n-1)) if m 1 and n 2 A(1, 0) = 0 A(0, 1) = A(2, 2) = A(1, 1) =

Ackermann’s Function A(m, n) = 2 n if m = 0 0 if m 1 and n = 0 2 if m 1 and n = 1 A(m-1, A(m, n-1)) if m 1 and n 2 A(1, 0) = 0 A(0, 1) = 2 A(2, 2) = A(1, 1) =

Ackermann’s Function A(m, n) = 2 n if m = 0 0 if m 1 and n = 0 2 if m 1 and n = 1 A(m-1, A(m, n-1)) if m 1 and n 2 A(1, 0) = 0 A(0, 1) = 2 A(2, 2) = A(1, A(2, 1)) = A(1, 2) = A(0, A(1, 1)) =A(0, 2) = 4 A(1, 1) =

Ackermann’s Function A(m, n) = 2 n if m = 0 0 if m 1 and n = 0 2 if m 1 and n = 1 A(m-1, A(m, n-1)) if m 1 and n 2 A(1, 0) = 0 A(0, 1) = 2 A(2, 2) = A(1, A(2, 1)) = A(1, 2) = A(0, A(1, 1)) =A(0, 2) = 4 A(1, 1) = 2

Show that A(m, 2) = 4 whenever m 1 A(m, n) = 2 n if m = 0 if m 1 and n = 0 = 2 if m 1 and n = 1 = A(m-1, A(m, n-1)) if m 1 and n 2 Basis step: When m = 1, A(1, 2) = A(0, A(1, 1)) = A(0, 2) = 2*2 = 4

Show that A(m, 2) = 4 whenever m 1 A(m, n) = 2 n if m = 0 if m 1 and n = 0 = 2 if m 1 and n = 1 = A(m-1, A(m, n-1)) if m 1 and n 2 Inductive Step: Assume that A(j, 2) = 4 for 1 j k. We must show that A(k+1, 2) = 4. A(k+1, 2) = A(k, A(k+1, 1) = A(k, 2) = 4

When n is a positive integer, show that Basis step: n = 1, remember f 0 =0, f 1 =1, f 2 =1

When n is a positive integer, show that Inductive step: Assume that We must show that

Prove that Proof: Basis Step: For n = 1 we get 1/(1(1+1)) = 1/2 for both the sum and the closed form. Inductive Step: Assume that We must show that