Proofs of Work POWs and Bread Pudding Protocols

Proofs of Work (POWs) and Bread Pudding Protocols Ari Juels RSA Laboratories with Markus Jakobsson Bell Laboratories

Cryptography: About proofs of mathematical relations Prover Verifier w = ge c s = cx +e s c g =y w?

Some proofs Proof of Identity = Cryptographic Authentication Protocol

Some proofs Proof of Authorization (Signed Document) = Digital signature

Proof of work? 1 ounce sweat = 1 hour of work We can make precise in cryptographic world

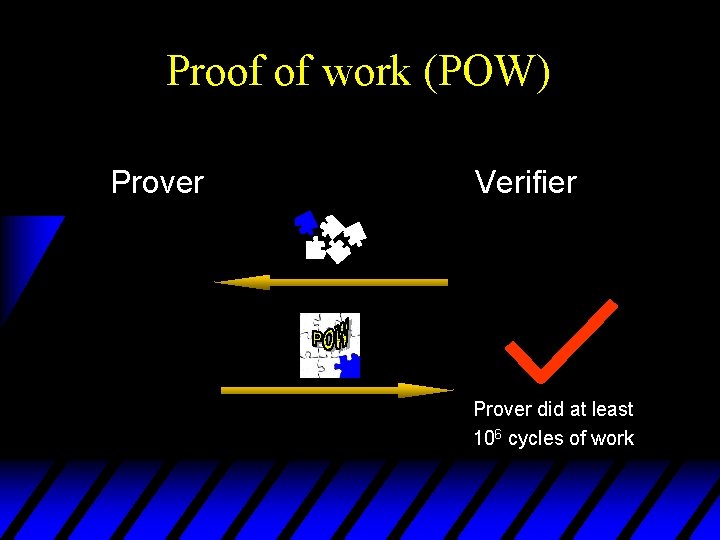
Proof of work (POW) Prover Verifier Query Response Prover did at least 106 cycles of work

Example of a POW (Hash inversion) Prover Verifier t = h(s) [k bits] random secret s Prover computed an expected 2 k-1 hashes s

What are POWs good for? u Spam deterrent (DN 94), “Hash cash” u Defense against denial-of-service attacks (JB 99) Service Request

What are POWs good for? u Benchmarking Query Client Response Server

Formal notion of POW

Breadpudding u Idea: Re-use the ``stale’’ computation in a POW to perform useful task u Achieve privacy in useful task u Example: Hash inversion POW for distributed Micro. Mint

Micro. Mint Want a scheme that mimics economics of physical mint u Verifying validity of a coin is easy u Base minting cost is high so. . . u Forgery is expensive

The minting process 1. Throw balls into bins using “random” function h 2. Any bin with two balls is a coin

Minting in Micro. Mint h Collision = Coin Bin 1 Bin 2 Bin 3 Bin 4 Bin 5 Bin 6 Bin 7 Bin 8 Bin 9

Checking a coin h Valid coin? Bin 2

Features u Many bins, so need to throw many balls to mint successfully u Minting requires very intensive computation

Minting requires special, e. g. , $250, 000 computer “Deep Crack”

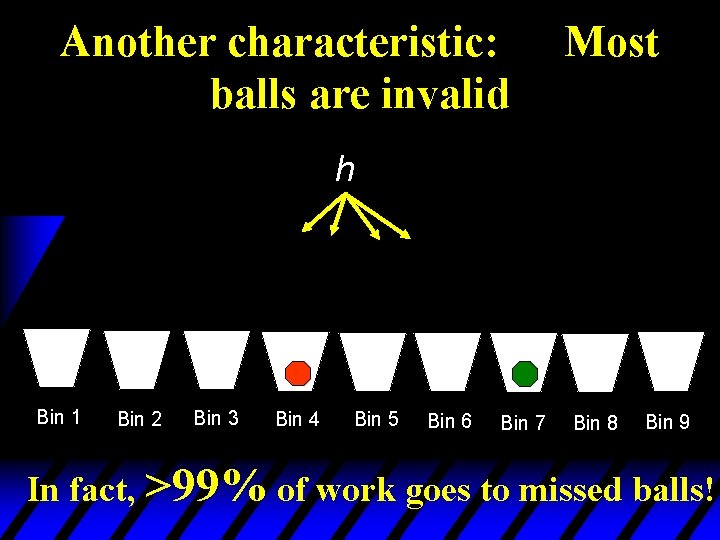
Another characteristic: balls are invalid Most h Bin 1 Bin 2 Bin 3 Bin 4 Bin 5 Bin 6 Bin 7 Bin 8 Bin 9 In fact, >99% of work goes to missed balls!

Idea: Make three stage process 1. Create “valid” balls, i. e. , balls that won’t miss (>99% of work) 2. Throw balls into bins using “random” function h (<1% of work) 3. Any bin with two balls is a coin

Have many other (untrusted) people do Step 1

Now. . . u 99%+ of work is done for minter u. No participant will get enough balls to do minting himself/herself (or else participants know “validity” h but not “throwing” h) u. Minting is cheap for minter!

Minter can use ordinary server

Questions? ? +