Recursive Definitions Rosen 3 4 Recursive or inductive









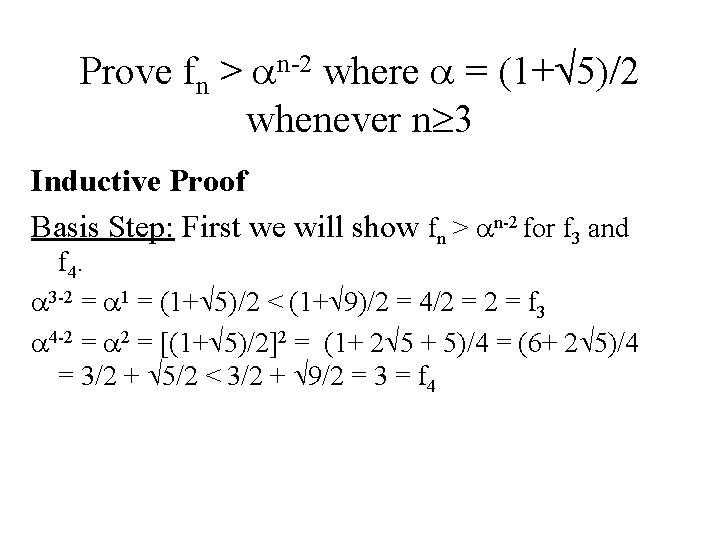

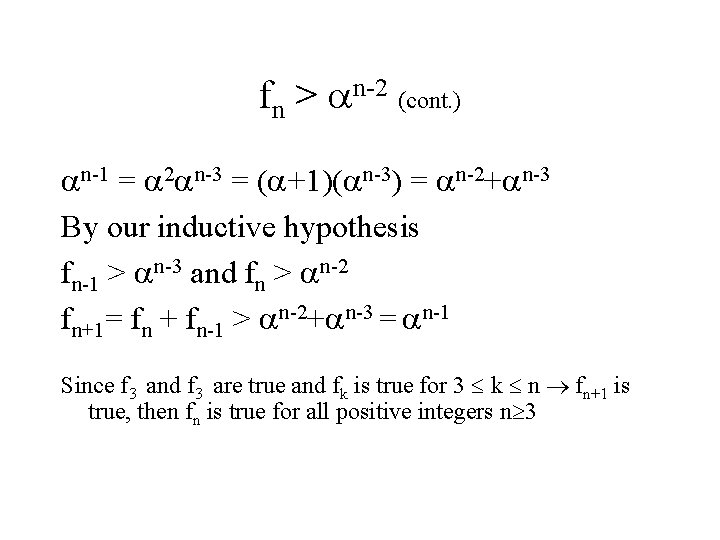




- Slides: 16

Recursive Definitions Rosen, 3. 4

Recursive (or inductive) Definitions • Sometimes easier to define an object in terms of itself. • This process is called recursion. – Sequences • {s 0, s 1, s 2, …} defined by s 0 = a and sn = 2 sn-1 + b for constants a and b and n Z+ – Sets • 3 S and x+y S if x S and y S – Functions • Example: f(n) = 2 n, f(n) = 2 f(n-1) and f(0) = 1

Recursively Defined Functions To define a function with the set of nonnegative integers as its domain 1. Specify the value of the function at zero (or sometimes, it first k terms). 2. Give a rule for finding its value at an integer from its values at smaller integers.

Examples of Recursively Defined Functions • Factorial Function n! § n! = n(n-1)(n-2)…. (1) § f(0) = 1, f(n) = n(f(n-1)) • an § f(0) = 1, f(n+1) = f(n)*a • Fibonacci Numbers § f 0=0, f 1=1, f n+1 = fn + f n-1 § {0, 1, 1, 2, 3, 5, 8, 13, . . . }

Prove that the nth term in the Fibonacci sequence is when n 2 Induction Proof: Basic Step: Let n = 2, then f 2 = 1 = =1+0 Inductive Step: Consider k 2 and assume that the expression is true for 2 n k. We must show that the expression is true for n = k+1, i. e. , that fk+1 = fk +fk-1 by definition by the inductive hypothesis

Fibonacci Proof (cont. ) Since f 2 is true and [fn is true for 2 n k fk+1] is true, then fn is true for all positive integers n 2.

Recursively Defined Set Example Let the set S be defined recursively as 3 S and x+y S if x S and y S. Prove that S is equal to the set of positive integers divisible by 3 (set A). Proof: To show that S = A, we must show that A S and that S A.

Recursive Set Example (cont. ) First we will show that A S. To do this we must show that every positive integer divisible by 3 is in S. This is the same as saying that 3 n is in S for n Z+. We will do an inductive proof. Let p(n) be the statement that 3 n S for n a positive integer. Basis Step: p(1) = 3 Inductive Step: We will show that p(n) p(n+1) Let p(n) S. Then p(n+1) = 3 n + 3. Since 3 n S and 3 S, then 3 n+3 S. Therefore every element in A must be in S.

Recursive Set Example (cont. ) Now we will show that S A. To do this we must show that every element in S is divisible by 3, i. e. , that it can be represented as 3(j) where j is a positive integer. Basis Step: 3 A since 3 = 3(1) Inductive Step: Assume x, y are in A (where x, y S). x and y are divisible by 3 since they are both in A. Therefore x = 3 j and y = 3 k for j, k Z+. Then z = x+y = 3 j+3 k = 3(j+k), which is divisible by 3, so z A (and by definition, z S). Therefore every element in S must be in A
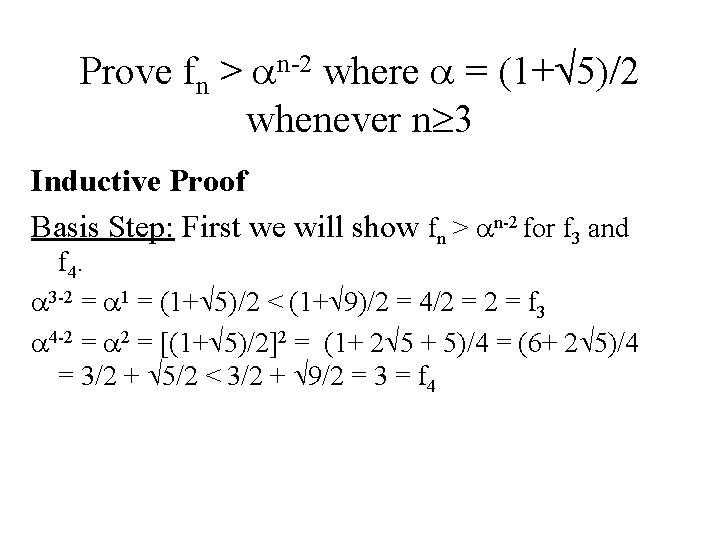
Prove fn > n-2 where = (1+ 5)/2 whenever n 3 Inductive Proof Basis Step: First we will show fn > n-2 for f 3 and f 4. 3 -2 = 1 = (1+ 5)/2 < (1+ 9)/2 = 4/2 = f 3 4 -2 = [(1+ 5)/2]2 = (1+ 2 5 + 5)/4 = (6+ 2 5)/4 = 3/2 + 5/2 < 3/2 + 9/2 = 3 = f 4

fn > n-2 (cont. ) Inductive Step: Assume that fk > k-2 is true for all nonnegative integers 3 k n when n>4. We must show that fn+1> n-1. Lemma: 2 = [(1+ 5)/2]2 = (1+2 5 +5)/4 = 3/2 + ( 5)/2 = 1 + (1+ 5)/2 = 1+
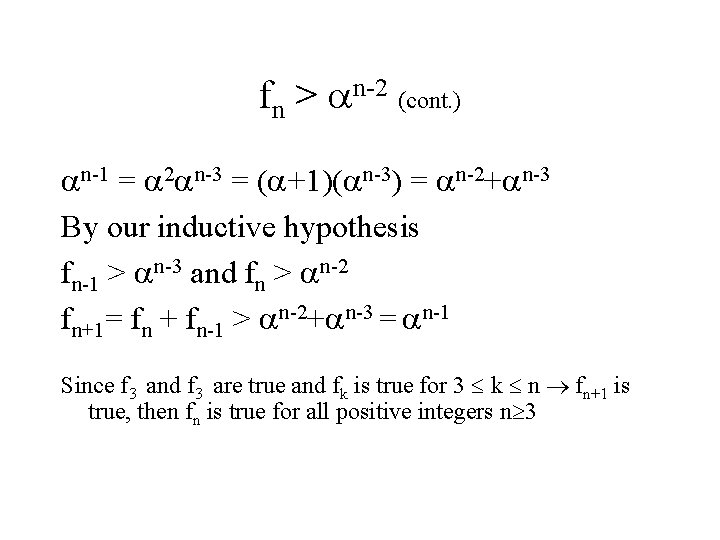
fn > n-2 (cont. ) n-1 = 2 n-3 = ( +1)( n-3) = n-2+ n-3 By our inductive hypothesis fn-1 > n-3 and fn > n-2 fn+1= fn + fn-1 > n-2+ n-3 = n-1 Since f 3 and f 3 are true and fk is true for 3 k n fn+1 is true, then fn is true for all positive integers n 3

Find a closed form solution to the recursive equation: T(n) = T(n-1) + c 1. T(0) = c 0 One approach is to write down several terms, guess what the equation is, and then prove that your guess is correct (or not) using an induction proof. T(0) = c 0 T(1) = T(0) + c 1 = c 0 + c 1 T(2) = T(1) + c 1 = c 0 + 2 c 1 T(3) = T(2) + c 1= c 0 + 3 c 1 T(4) = T(3) + c 1= c 0 + 4 c 1 Guess that T(n) = c 0 + nc 1

Induction proof Basis Step: for n = 0, T(0) = c 0 + (0)c 1 = c 0 Inductive Step: Assume that T(n) = c 0 + nc 1, we must show that T(n+1) = c 0 + (n+1)c 1. T(n+1) = T(n) + c 1 = c 0 + nc 1 + c 1 = c 0 + (n+1)c 1.

Find a closed form solution to T(1) = c 0, T(n) = 2 T(n-1)+c 1 T(1) = c 0 T(2) = 2 T(1) + c 1 = 2 c 0 + c 1 T(3) = 2 T(2)+c 1 = 2(2 c 0+c 1)+c 1 = 4 c 0+3 c 1 T(4) = 2 T(3)+c 1 = 2(4 c 0+3 c 1)+c 1 = 8 c 0+7 c 1 T(5) = 2 T(4)+c 1 = 2(8 c 0+7 c 1)+c 1 = 16 c 0+15 c 1 Guess that T(n) = 2 n-1 c 0 + (2 n-1 -1)c 1

Prove that T(1) = c 0, T(n) = 2 T(n-1)+c 1 has closed form solution T(n) = 2 n-1 c 0 + (2 n-1 -1)c 1 Basis Step: T(1) = 21 -1 c 0 + (21 -1 -1)c 1 = c 0 Induction Step: Assume that T(n) = 2 n-1 c 0 + (2 n-1 -1)c 1. We must show that T(n+1) = 2(n+1)-1 c 0 + (2(n+1)-1 -1)c 1 = 2 nc 0 + (2 n-1)c 1. T(n+1) = 2 T(n) + c 1 = 2[2 n-1 c 0 + (2 n-1 -1)c 1]+ c 1 = 2 nc 0 + (2 n-2)c 1 + c 1 = 2 nc 0 + 2 nc 1 - c 1 = 2 nc 0 + (2 n-1)c 1.
 Eddie rosen brian rosen
Eddie rosen brian rosen Rot rot rot sind die rosen rosen die ich an dich verschenke
Rot rot rot sind die rosen rosen die ich an dich verschenke Recursive definitions and structural induction
Recursive definitions and structural induction Non recursive algorithm example
Non recursive algorithm example David rosen sega
David rosen sega Gibt es schwarze rose
Gibt es schwarze rose Sophie rosen
Sophie rosen Epr einstein podolsky rosen
Epr einstein podolsky rosen Von rosen ortezi
Von rosen ortezi John rosen
John rosen Kenneth rosen discrete mathematics solutions
Kenneth rosen discrete mathematics solutions Homogeneous transform
Homogeneous transform Ncblpc
Ncblpc The car trip michael rosen
The car trip michael rosen Andy rosen basketball
Andy rosen basketball Quadruple constraints in project management
Quadruple constraints in project management Strart
Strart