Geometry Lesson 2 5 Postulates and Paragraph Proofs

Geometry Lesson 2 – 5 Postulates and Paragraph Proofs Objective: Identify and use basic postulates about points, lines, and planes. Write paragraph proofs.

Postulate (or axiom) – a statement that is accepted as true without proof.

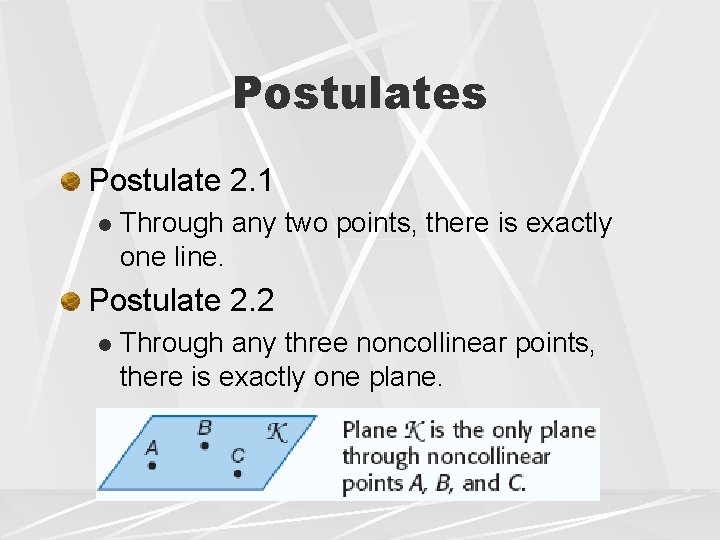
Postulates Postulate 2. 1 l Through any two points, there is exactly one line. Postulate 2. 2 l Through any three noncollinear points, there is exactly one plane.

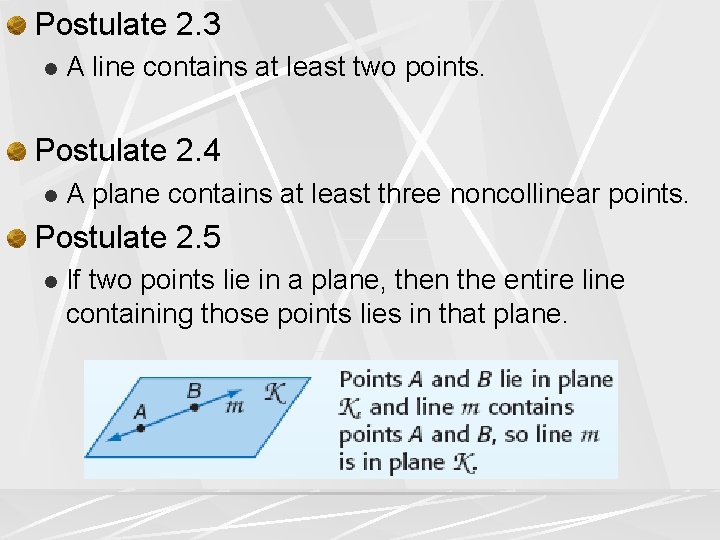
Postulate 2. 3 l A line contains at least two points. Postulate 2. 4 l A plane contains at least three noncollinear points. Postulate 2. 5 l If two points lie in a plane, then the entire line containing those points lies in that plane.

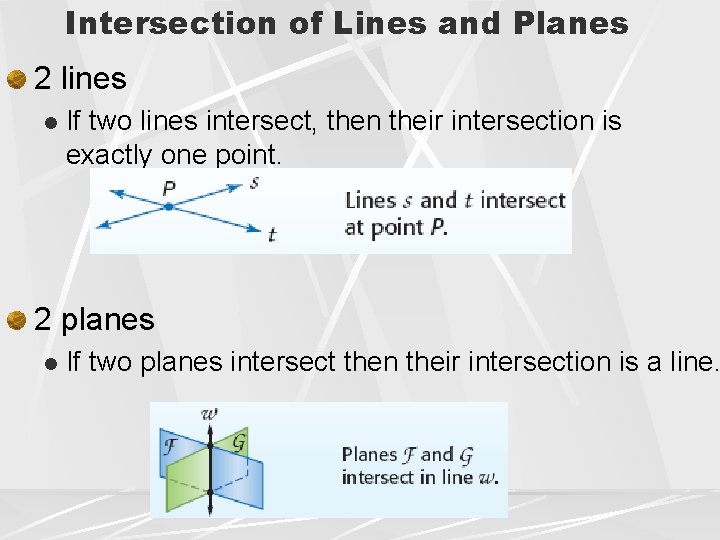
Intersection of Lines and Planes 2 lines l If two lines intersect, then their intersection is exactly one point. 2 planes l If two planes intersect then their intersection is a line.

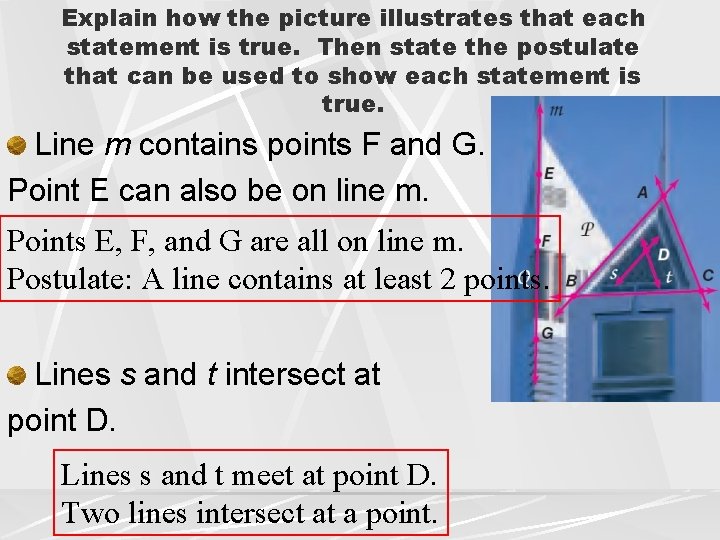
Explain how the picture illustrates that each statement is true. Then state the postulate that can be used to show each statement is true. Line m contains points F and G. Point E can also be on line m. Points E, F, and G are all on line m. Postulate: A line contains at least 2 points. Lines s and t intersect at point D. Lines s and t meet at point D. Two lines intersect at a point.

Determine whether each statement is sometimes, always, or never true. Explain your reasoning. If two coplanar lines intersect, then the point of intersection lies in the same plane as the two lines. Always, if two points lie in a plane, then the entire line containing those points lies in that plane. Four points are noncollinear Sometimes, a line contains at least 2 points, but the other points may or may not be on the same line.

Two lines determine a plane Always, there at least 3 noncollinear points to determine a plane. Three lines intersect in two points. Never, cannot meet at 2 points. If plane T contains EF and EF contains point G, then plane T contains point G. Always, if 2 points lie in a plane then the line Containing those points lies in the plane. GH contains thee noncollinear points. Never, noncollinear points cannot be on the same line.

Proof – used to prove a conjecture using deductive reasoning to move from the hypothesis to the conclusion of the conjecture you are trying to prove. l Logical argument in which each statement you make is supported by a statement that is accepted as true.

General outline

Write a proof Given that M is the midpoint of XY write a paragraph proof to show that Step 1: draw a picture to help Proof: Given: M is the midpoint of XY. Prove: If M is the midpoint of segment XY, then by definition of midpoint XM = MY. By definition of congruence if the measures are equal, then the segments are congruent. Thus,

Theorem 2. 1 Midpoint Theorem l If M is the midpoint of AB, then

Homework Pg. 128 1 – 13 all, 16 – 30 E