4 5 Segment and Angle Proofs Basic geometry

4. 5 Segment and Angle Proofs

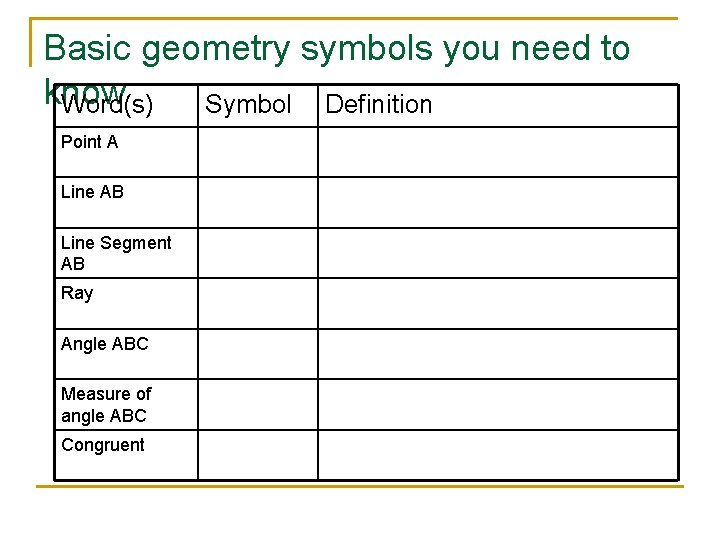
Basic geometry symbols you need to know Word(s) Symbol Definition Point A Line AB Line Segment AB Ray Angle ABC Measure of angle ABC Congruent

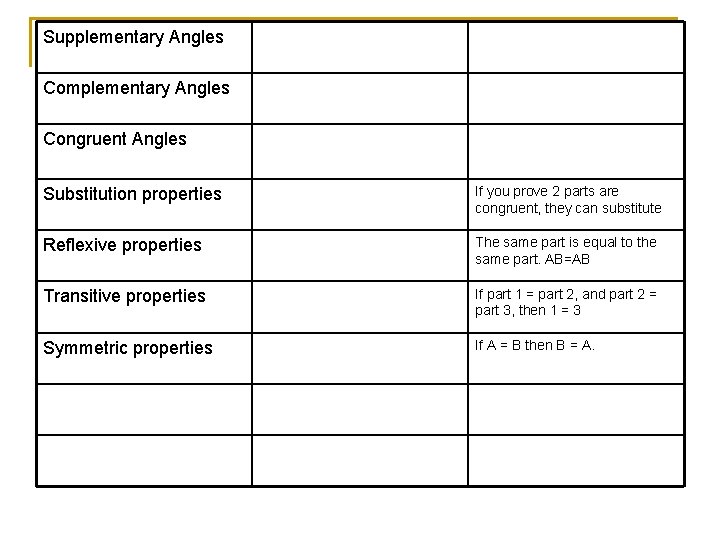
Supplementary Angles Complementary Angles Congruent Angles Substitution properties If you prove 2 parts are congruent, they can substitute Reflexive properties The same part is equal to the same part. AB=AB Transitive properties If part 1 = part 2, and part 2 = part 3, then 1 = 3 Symmetric properties If A = B then B = A.

Vocabulary n Proof – a logical argument that shows a statement is true n Two – column proof – numbered statements in one column, corresponding reason in other § Statement Reasons

n Postulate – a rule that is accepted without proof. Write forwards and backwards – reverse it and it‘s still true n Segment Addition Postulate -if B is between A and C, then AB + BC = AC converse…. . Reverse it…. - if AB + BC = AC, then B is between A and C Draw it….

n Angle Addition Postulate – n - If P is the interior (inside) of <RST then the measure of < RST is equal to the sum of the measures of <RSP and <PST. n Draw it -

Theorem – a statement that can be proven n Theorem 4. 1 – Congruence of Segments n Reflexive – n Symmetric – n Transitive – n Theorem 4. 2 – Congruence of Angles n Reflexive n Symmetric n Transitive

EXAMPLE 1 Write a two-column proof for the situation in Example 4 from Lesson 2. 5. GIVEN: m∠ 1 = m∠ 3 PROVE: m∠ EBA = m∠ DBC STATEMENT 1. 2. 3. 4. 5. m∠ m∠ m∠ REASONS 1. 1 = m∠ 3 EBA = m∠ 3 + m∠ 22. EBA = m∠ 1 + m∠ 23. 1 + m∠ 2 = m∠ DBC 4. EBA = m∠ DBC 5. Given Angle Addition Postulate Substitution Property of Equality Angle Addition Postulate Transitive Property of Equality

GUIDED PRACTICE for Example 1 ANSWER GIVEN : AC = AB + AB PROVE : AB = BC STATEMENT REASONS 1. AC = AB + AB 1. Given 2. AB + BC = AC 2. Segment Addition Postulate 3. AB + AB = AB + BC 3. Transitive Property of Equality 4. AB = BC 4. Subtraction Property of Equality

EXAMPLE 2 Name the property shown Name the property illustrated by the statement. a. If T and R b. If NK T BD , then BD P, then R P. NK. SOLUTION a. Transitive Property of Angle Congruence b. Symmetric Property of Segment Congruence

GUIDED PRACTICE for Example 2 Name the property illustrated by the statement. 2. CD CD ANSWER Reflexive Property of Congruence 3. If Q V, then V Q. ANSWER Symmetric Property of Congruence

Solving for x. n Based on the properties learned, if you know 2 “parts” are congruent, you set them equal to each other and solve. n m<A=2 x+15, m<B=4 x-3 2 x+15=4 x-3 15=2 x-3 18=2 x 9=x 2(9)+15=18+15=33 n n n A B

EXAMPLE 3 Use properties of equality Prove this property of midpoints: If you know that M is the midpoint of AB , prove that AB is two times AM and AM is one half of AB. GIVEN: M is the midpoint of AB. PROVE: a. AB = 2 AM 1 b. AM = 2 AB

EXAMPLE 3 Use properties of equality STATEMENT 1. M is the midpoint of AB. 2. AM MB 3. AM = MB 4. AM + MB = AB 5. AM + AM = AB a. 6. 2 AM = AB b. 7. AM = 1 AB 2 REASONS 1. Given 2. 3. 4. 5. Definition of midpoint Definition of congruent segments Segment Addition Postulate Substitution Property of Equality 6. Distributive Property 7. Division Property of Equality

EXAMPLE 4 Solve a multi-step problem GIVEN: B is the midpoint of AC. C is the midpoint of BD. PROVE: AB = CD STATEMENT REASONS 1. B is the midpoint of AC. 1. Given C is the midpoint of BD. 2. AB BC 2. Definition of midpoint 3. BC CD 3. Definition of midpoint 4. AB CD 4. Transitive Property of Congruence 5. AB = CD 5. Definition of congruent segments