Rcursivit 1 Introduction Une fonction rcursive est une

Récursivité 1

Introduction § Une fonction récursive est une fonction qui s'appelle même. § Directement (si la fonction P appelle directement P , on dit que la récursivité est directe). § Indirectement à travers une ou plusieurs fonctions relais (si P appelle une fonction P 1 , qui appelle une fonction P 2 , . . . , qui appelle une fonction Pn et qui enfin appelle P , on dit qu'il s'agit d'une récursivité indirecte). 2

Introduction § Si f est une fonction comprenant un appel à elle même, soit directement ou indirectement, alors f est une fonction récursive. § directement : int f 1( …) { . . . x= f 1(…); } § indirectement : int f 1( …) { . . . x= f 2(…); } int f 2(. . . ) { . . . x=f 1(. . . ); } 3

Introduction § La récursivité est une manière simple et élégante de résoudre certains problèmes algorithmiques. § Elle permet: § d'écrire des programmes beaucoup plus lisibles; § d'écrire d'une manière très rapide (par rapport d’une manière itérative); § d’utiliser le principe diviser-pour-résoudre. 4

Introduction § La récursivité utilise toujours la pile du programme en cours. § Dans une fonction récursive, toutes les variables locales sont stockées dans la pile, et empilées autant de fois qu'il y a d'appels récursifs. § La pile se remplit progressivement, et si on ne fait pas attention on arrive à un "débordement de pile". Ensuite, les variables sont désempilées. § Toute fonction récursive comporte une instruction (ou un bloc d'instructions) nommée "point terminal" ou "point d'appui" ou "point d'arrêt", qui indique le reste des instructions ne doit plus être exécuté. 5

Définition récursive § La fonction récursive est composée de deux partie: une partie strictement récursive et une partie non récursive (base) servant de point de départ à l'utilisation de la définiton récursive. § Structure générale d’une fonction récursive : { } if(/* !condition de convergence */) exit(1); if(/*condition d’arrêt*/) return(/*Ce qu’elle doit retourner*/); else appel récursif Traitement 6

Définition récursive § On peut définir le factoriel d'un nombre n non négatif de deux manières: § définition non récursive: n ! = n * n-1 *. . . 2 * 1 § définition récursive: n ! = n * (n-1) ! et 0 ! = 1 7

Définition récursive § Expression récursive du problème : n ! = n * n-1 *. . . 2 * 1 = n*(n-1)! § Condition d’arrêt : n = 1 ou n = 0 § Convergence (vers la condition d’arrêt): § Si n=1 ou n=0, alors on a convergé! § Si n>1, alors la soustraction à l’étape suivante nous approche de n=1. Donc si n est une entier non négatif ça converge! 8

Fonctions récursives § La grande question qui se pose dans une fonction récursive est celle de l'arrêt de la récursivité (de sortie). § La condition de sortie pour la fonction n! est 0!=1. § Le choix de la condition - vous devrez être sûr qu'elle soit validée à un moment ou à un autre sinon c'est comme si vous créez une boucle infinie sans condition de sortie ! § La syntaxe la plus générale d'une fonction récursive est : <type_de_retour> <nom. Fct>(< args >){ [déclaration de variables] [test d'arrêt] [suite d'instructions] [appel de <nom. Fct>(< args‘ >)] [suite d'instructions] return <résultat>; } 9

Fonctions récursives § Premier exemple - calcul de n!. (0!=1!=1 et n! = n * (n-1)!). § De manière itérative, on écrit : unsigned long factorielle(int n){ unsigned long f = 1; for(int k = n; k > 1; k--) f *= k; return f; } le calcul par accumulation du produit dans la variable f 10

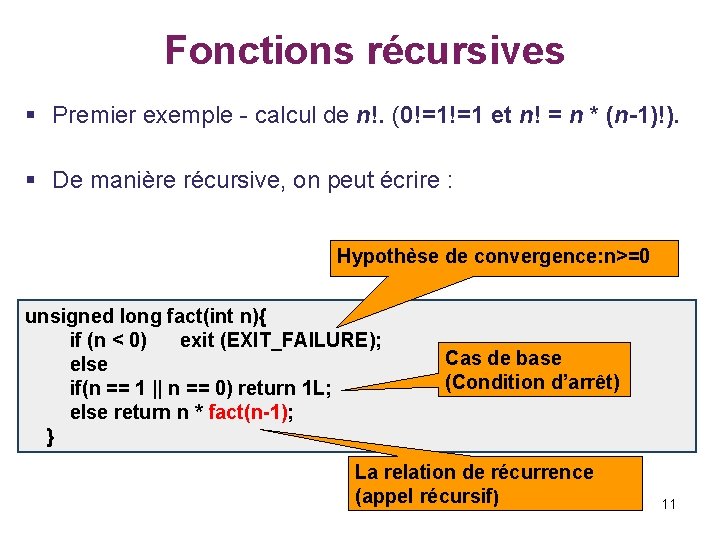
Fonctions récursives § Premier exemple - calcul de n!. (0!=1!=1 et n! = n * (n-1)!). § De manière récursive, on peut écrire : Hypothèse de convergence: n>=0 unsigned long fact(int n){ if (n < 0) exit (EXIT_FAILURE); else if(n == 1 || n == 0) return 1 L; else return n * fact(n-1); } Cas de base (Condition d’arrêt) La relation de récurrence (appel récursif) 11

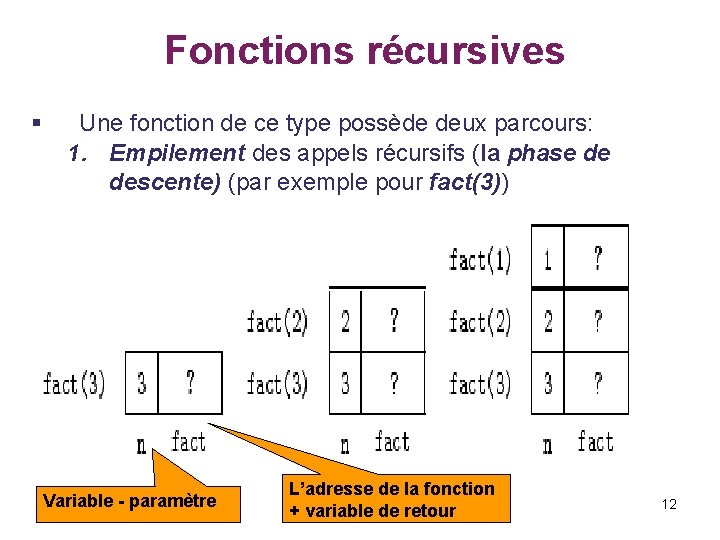
Fonctions récursives Une fonction de ce type possède deux parcours: Empilement des appels récursifs (la phase de 1. descente) (par exemple pour fact(3)) § Variable - paramètre L’adresse de la fonction + variable de retour 12

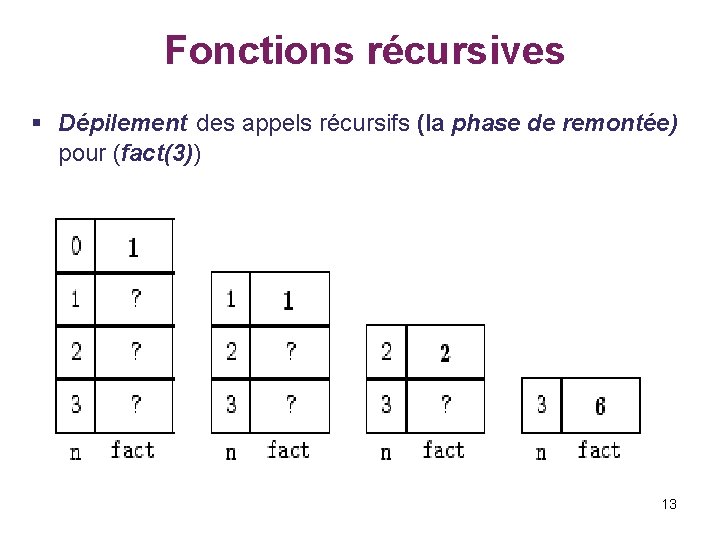
Fonctions récursives § Dépilement des appels récursifs (la phase de remontée) pour (fact(3)) 13

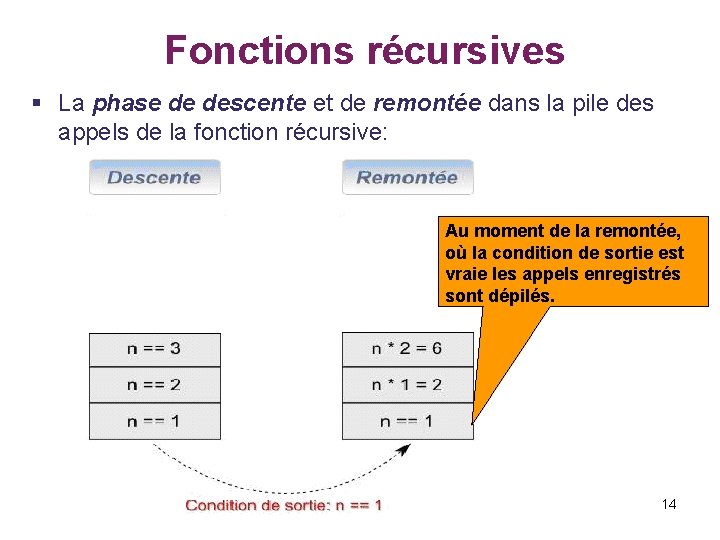
Fonctions récursives § La phase de descente et de remontée dans la pile des appels de la fonction récursive: Au moment de la remontée, où la condition de sortie est vraie les appels enregistrés sont dépilés. 14

Fonctions récursives § La récursivité ne marche que si on ne fait pas déborder la pile d'appels. unsigned long fact(int n){ if (n < 0) exit (EXIT_FAILURE); else if(n == 1 || n == 0) return 1 L; else return n * fact(n+1); } La fonction ne termine pas § Le problème fondamental de l'informatique de pouvoir prouver qu'une fonction (ou un algorithme) termine. 15

Fonctions récursives Variables locales, arguments de fonctions § Lorsqu'une fonction récursive définit des variables locales, un exemplaire de chacune d'entre elles est crée à chaque appel récursif de la fonction. § Il en est de même des arguments des fonctions. 16

Fonctions récursives Variables locales, arguments de fonctions § Exemple - considérons une fonction void miroir() qui lit caractère par caractère une chaîne terminée par '? ' et l'affiche dans l'ordre inverse de celui de la lecture. § Version non récursive #include <stdio. h> void miroir() { char s[20], c; int i=0; while( (c=getchar())!='? ') s[i++]=c; s[i]=''; Entrer les caracteres avec ? a la fin. while (--i>=0) abcd? putchar (s[i]); dcba } void main() { printf("Entrer les caracteres avec ? a la fin. n"); miroir(); } 17

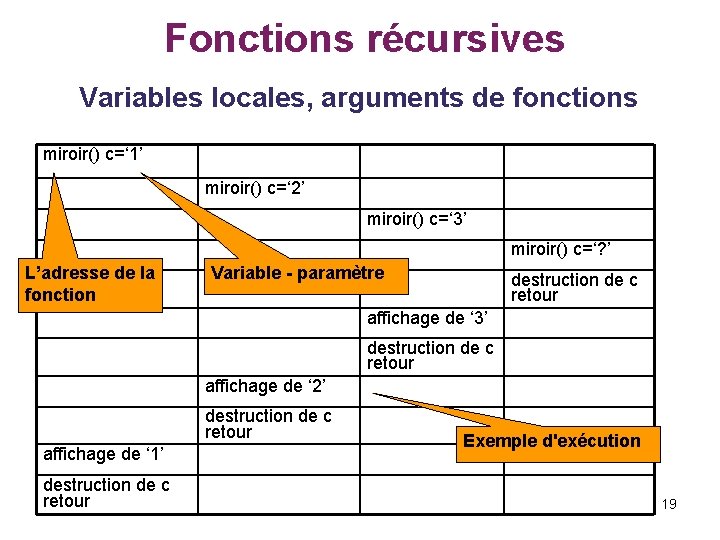
Fonctions récursives Variables locales, arguments de fonctions § Exemple - considérons une fonction void miroir() récursive qui lit caractère par caractère une chaîne terminée par '? ' et l'affiche dans l'ordre inverse de celui de la lecture. § Version récursive sans variable locale -> un tableau pour stocker tous les caractères jusqu'au caractère '? ' pour ensuite les afficher dans l'ordre inverse. void miroir() { int c = getchar(); if (c != '? ') { miroir(); printf("%c", c); Entrer les caracteres avec ? a la fin. } 123? } 321 void main() { printf("Entrer les caracteres avec ? a la fin. n"); miroir(); } 18

Fonctions récursives Variables locales, arguments de fonctions miroir() c=‘ 1’ miroir() c=‘ 2’ miroir() c=‘ 3’ L’adresse de la fonction affichage de ‘ 1’ destruction de c retour miroir() c=‘? ’ Variable - paramètre destruction de c retour affichage de ‘ 3’ destruction de c retour affichage de ‘ 2’ destruction de c retour Exemple d'exécution 19

Fonctions récursives Dangers et précautions 1. Dépassement de capacité § Il est d'usage de choisir un type approprié, même si vous êtes certains que le type que vous avez choisi ne sera jamais dépassé. Utilisez tant que possible une variable pouvant contenir de plus grandes données. Ceci s'applique à tous types de données. Evitez le type int si vous travaillez avec une fonction récursive. § § § 20

Fonctions récursives Dangers et précautions 2. Débordement de pile (Stack Overflow) § Dans la pile sont non seulement stockés les valeurs des variables de retour mais aussi les adresses des fonctions entre autres choses, les données sont nombreuses et un débordement de la pile peut très vite arriver ce qui provoque sans conteste une sortie anormale du programme. § Dans l'exemple de la fonction factoriel, il nous faut (en arrondissant) environ 135000 appels récursifs pour faire exploser la pile. § Si vous êtes presque sûr de dépasser ce genre de limites, préférez alors une approche itérative plutôt qu'une approche récursive du problème. 21

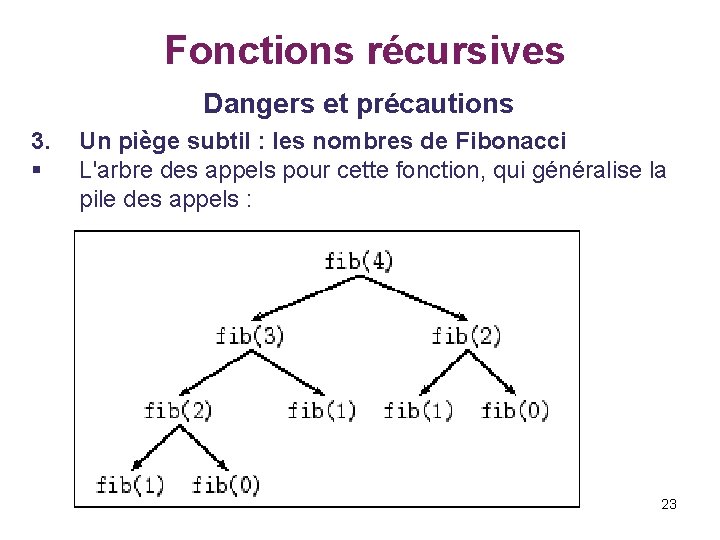
Fonctions récursives Dangers et précautions 3. Un piège subtil : les nombres de Fibonacci § Exemple - écrire une fonction qui calcule le n-ième terme de la suite de Fibonacci, définie par F 0 = 0, F 1 = 1 et pour n≥ 2, Fn = Fn-1 + Fn-2. long fib(int n){ if(n <= 1) return n; // cas de base else return fib(n-1)+fib(n-2); } § § Le programme marche, il termine. Le problème se situe dans le nombre d'appels à la fonction. On fait un nombre exponentiel d'appels à la fonction. 22

Fonctions récursives Dangers et précautions 3. Un piège subtil : les nombres de Fibonacci § L'arbre des appels pour cette fonction, qui généralise la pile des appels : 23

Fonctions récursives Dangers et précautions 3. Un piège subtil : les nombres de Fibonacci § Une façon de calculer Fn qui ne coûte que n appels est la suivante. § On calcule les valeurs du couple (Fi, Fi+1). long fib(int n){ int i, u, v, w; // u = F(0); v = F(1) u = 0; v = 1; for(i = 2; i <= n; i++){ // u = F(i-2); v = F(i-1) w = u+v; u = v; v = w; } return v; } 24

Fonctions récursives Diviser pour résoudre § § § Quand on ne sait pas résoudre un problème, on essaie de le couper en morceaux qui seraient plus faciles à traiter. Exemple - Recherche d'une racine par dichotomie On suppose que f : [a, b] → R est continue et telle que f(a) < 0, f(b) > 0. Il existe une racine x 0 de f dans l'intervalle [a, b], qu'on veut déterminer de sorte que |f(x 0)| ≤ ε pour ε donné. On calcule f((a+b)/2). En fonction de son signe, on explore [a, m] ou [m, b]. 25

Fonctions récursives Diviser pour résoudre § Exemple #include <stdio. h> 1/2 Programmer la fonction f. #include <math. h> double f(double x){ return x*x*x-2; } double racine. Dicho(double a, double b, double eps){ double m = (a+b)/2; double fm = f(m); La fonction qui cherche la if(abs(fm) <= eps) racine return m; if(fm < 0) // la racine est dans [m, b] return racine. Dicho(m, b, eps); else // la racine est dans [a, m] return racine. Dicho(a, m, eps); } 26

Fonctions récursives Diviser pour résoudre § Exemple void main() {double a, b, eps; do { printf("a="); scanf("%lf", &a); printf("b="); a=1 scanf("%lf", &b); b=6 } while (a >= b); eps=0. 01 do { La racine=1. 312500 printf("eps="); scanf("%lf", &eps); } while(eps>1); printf("Le racine=%lfn", racine. Dicho(a, b, eps)); } 27

Fonctions récursives terminales § § Lorsqu'il s'agit de faire de plus profondes récursions, un autre type de fonction récursive existe - c'est la récursivité terminale. Une grille de Loto contient 49 numéros dont seulement 6 peuvent êtres tirés. Le calcule le factoriel de 49 donne: 49! = 49 x 48 x 47. . . 8 x 7 x 6! Le résultat obtenu est d'une grandeur inimaginable ! 28

Fonctions récursives terminales § § Avec une récursivité normale, on a (49 -6)x 2 passages soit 43 appels empilés l'un après l'autre sans compter qu'il faut également remonter tous les appels ce qui nous fait un total de 86 passages. La perte de temps sur des récursions encore plus profondes et qui risqueraient par ailleurs de faire exploser la pile ce qui conduirait irrémédiablement au plantage du programme ! La récursion terminale - c'est une récursion avec uniquement une phase de descente, sans remontée. De cette manière on économise l'utilisation de la pile du programme, et on gagne du temps en exécution. 29

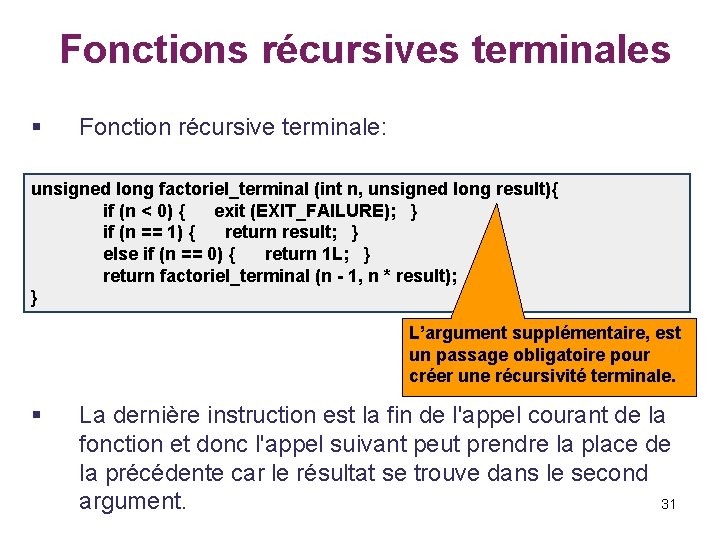
Fonctions récursives terminales § Ceci est possible car la dernière expression return factoriel_terminale (. . . ) renvoie directement la valeur obtenue par l'appel récursif courant, sans qu'il n'y ait d'autres opérations à faire, ce qui n'est pas le cas dans la fonction récursive simple, où l'on multiplie n par le retour de la fonction. § Les appels de la fonction n'ont pas besoin d'êtres empilés car l'appel suivant remplace simplement l'appel précédent dans le contexte d'exécution. 30

Fonctions récursives terminales § Fonction récursive terminale: unsigned long factoriel_terminal (int n, unsigned long result){ if (n < 0) { exit (EXIT_FAILURE); } if (n == 1) { return result; } else if (n == 0) { return 1 L; } return factoriel_terminal (n - 1, n * result); } L’argument supplémentaire, est un passage obligatoire pour créer une récursivité terminale. § La dernière instruction est la fin de l'appel courant de la fonction et donc l'appel suivant peut prendre la place de la précédente car le résultat se trouve dans le second 31 argument.

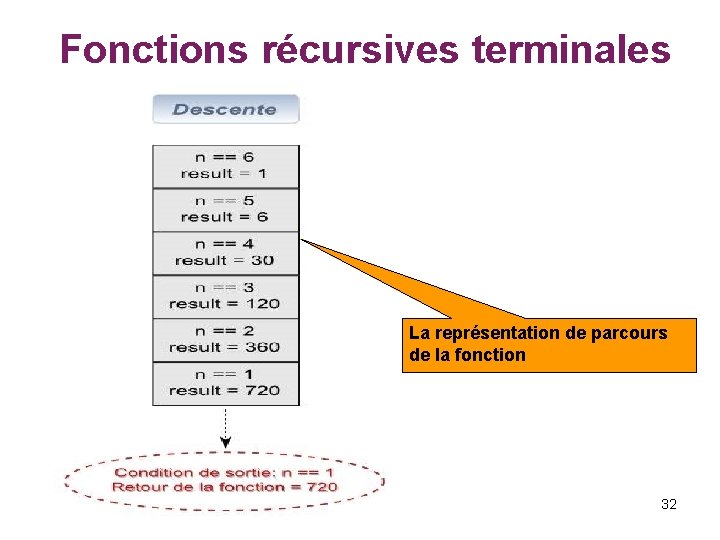
Fonctions récursives terminales La représentation de parcours de la fonction 32

Fonctions récursives Quand utiliser la récursivité § § § Quand il existe une définition récursive claire. Quand la récursivité est plus simple que la version itérative. Quand on a besoin d’un gain en performance possible grâce à une formulation récursive habile. § Généralement rapide et simple pour le développement. § Temps de mise au point ( «débogage » ) peut être long. § Elle est lourde à l’exécution 33