Gradient dune fonction Gnralits La notion de gradient

Gradient d’une fonction

Généralités § § La notion de gradient est d’un usage courant : on parle du gradient de température, gradient de concentration. . . En électromagnétisme on effectue souvent des calculs de variations de grandeurs scalaires ou vectorielles. La variation par rapport à x d’une fonction à plusieurs variables est obtenue en calculant la dérivée par rapport à x de cette fonction en considérant y et z comme des constantes ; on parle alors de dérivée partielle La variation d’une fonction de plusieurs variables qui résulterait de petites variations simultanées des variables x, y et z est la somme des dérivées partielles

Produit scalaire de deux vecteurs La variation de la fonction f(x, y, z) s ’écrit Cette expression est identique au produit scalaire de deux vecteurs le vecteur déplacement un vecteur de coordonnées Ce vecteur est – confondu avec l’opérateur dérivée partielle – appelé gradient de la fonction f(x, y, z) – noté Cet opérateur vectoriel n’est qu’un outil mathématique destiné à rendre compte des réalités simples et concrètes .

Caractéristiques du vecteur gradient Direction Soit un déplacement d. M sur la surface f=constante M f constante

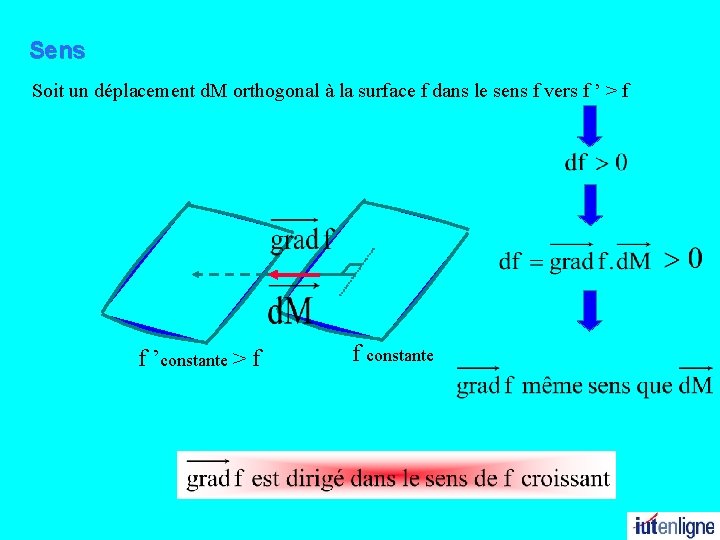
Sens Soit un déplacement d. M orthogonal à la surface f dans le sens f vers f ’ > f f ’constante > f f constante

Caractéristiques du vecteur l normal à la surface iso-f l dirigé dans le sens des f croissants l de coordonnées cartésiennes f 2 > f 1 constante

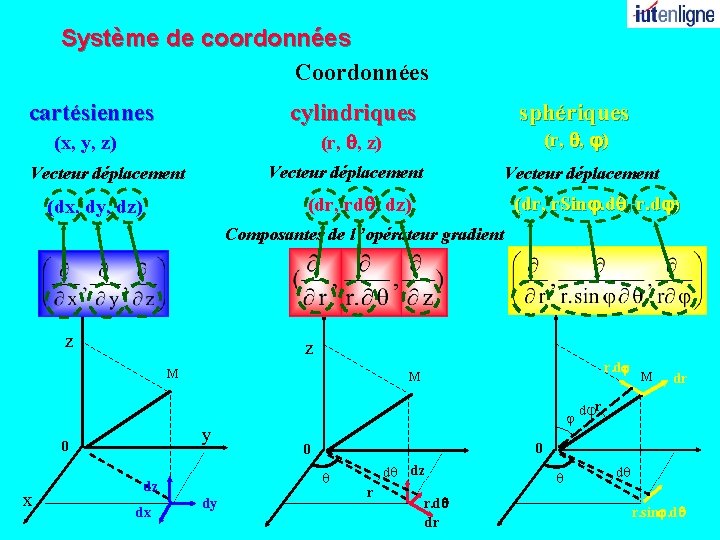
Système de coordonnées Coordonnées cartésiennes cylindriques sphériques (r, q, z) (r, q, j) (x, y, z) Vecteur déplacement (dr, r. Sinj. dq, r. dj) (dr, rdq, dz) (dx, dy, dz) Composantes de l ’opérateur gradient z z M y 0 x j dy M dr djr 0 0 q dz dx r. dj M dq dz r r. dq dr q dq r. sinj. dq

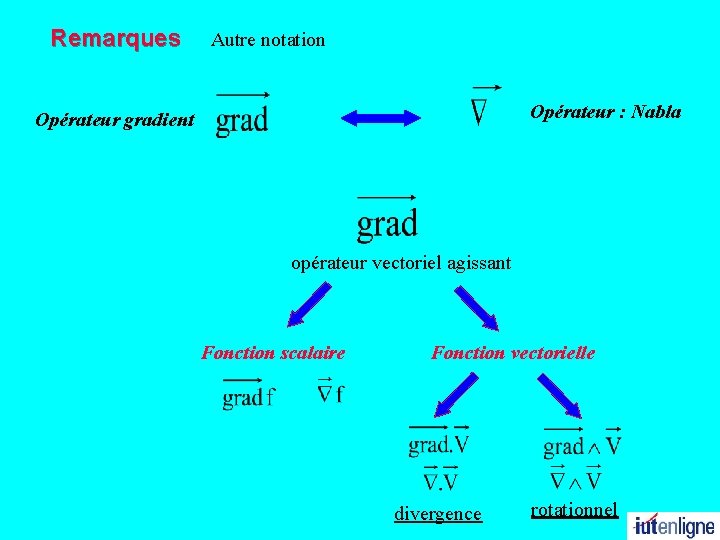
Remarques Autre notation Opérateur : Nabla Opérateur gradient opérateur vectoriel agissant Fonction scalaire Fonction vectorielle divergence rotationnel

Gradient d ’une fonction La variation d’une fonction de plusieurs variables Cette expression est identique au produit scalaire de deux vecteurs gradient f Le vecteur gradient est – confondu avec l’opérateur dérivée partielle – noté ou – perpendiculaire à la surface f constante – dirigé dans le sens des f croissants déplacement

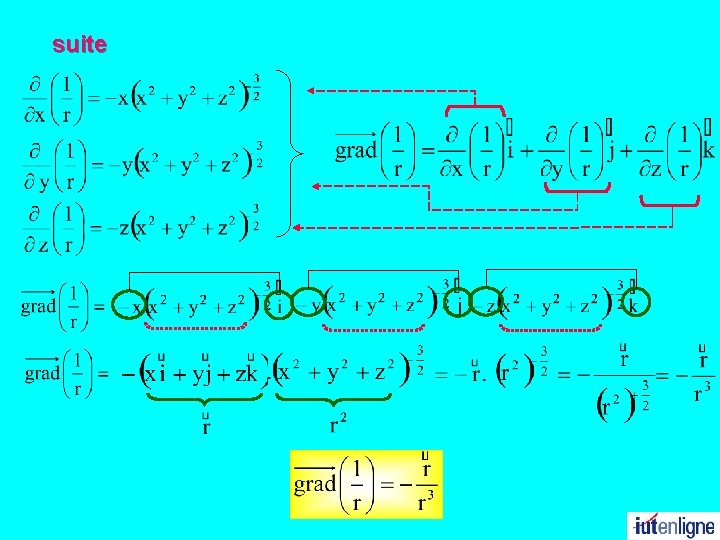
z Exercice M r calculer 0 x En coordonnées cartésiennes (un) ’=n. un-1. u ’ de la même façon y

suite

Théorème du gradient Si un vecteur est représentable comme le gradient d’une fonction scalaire f L’intégrale d’un vecteur le long d’un chemin est appelée circulation du vecteur Ø La circulation d ’un tel vecteur Ø est indépendante du chemin suivi Ø ne dépend que du point de départ et d ’arrivée Ø si la boucle est fermée, la circulation est nulle

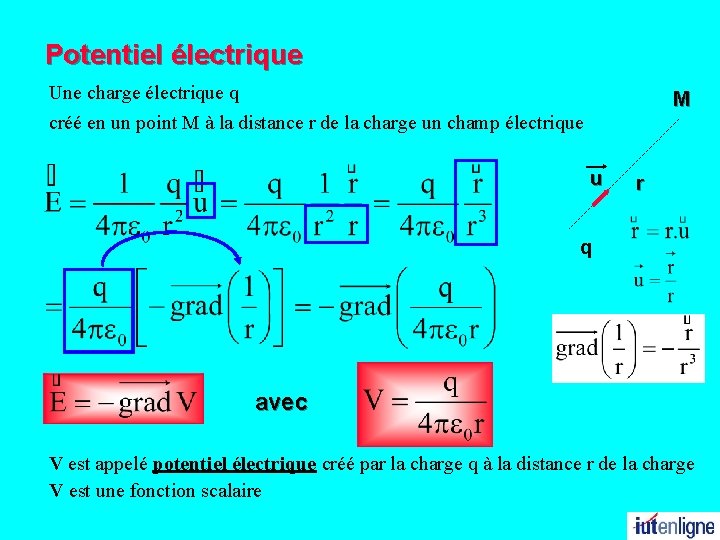
Potentiel électrique Une charge électrique q M créé en un point M à la distance r de la charge un champ électrique u r q avec V est appelé potentiel électrique créé par la charge q à la distance r de la charge V est une fonction scalaire

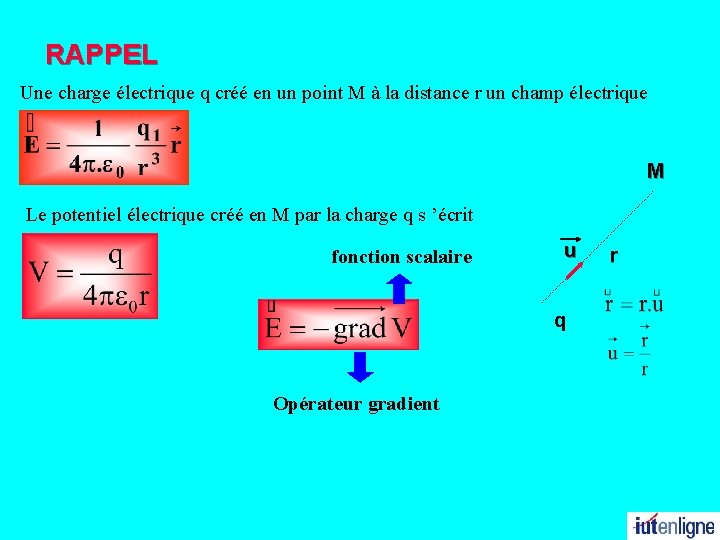
RAPPEL Une charge électrique q créé en un point M à la distance r un champ électrique M Le potentiel électrique créé en M par la charge q s ’écrit fonction scalaire u q Opérateur gradient r

Application du théorème du gradient Ø La tension électrique UAB entre les points A et B est égale à la circulation du champ électrostatique entre ces deux points si la courbe est fermée

Commentaires 0 0 Ø L ’unité de potentiel électrique est le Volt Ø Ø Le potentiel est défini à une constante près On ne peut pas mesurer un potentiel V On ne peut que mesurer des différences de potentiel entre deux points Ø Il est souvent plus aisé de déterminer Ø Ø le potentiel créé par une distribution de charges Ø on calcule le gradient du potentiel Ø le champ par E=-grad. V Ø Composante radiale de

Commentaires (suite) l Le potentiel créé par une distribution discrète de charges l Le potentiel créé par une distribution continue de charges distribution linéique distribution surfacique distribution volumique

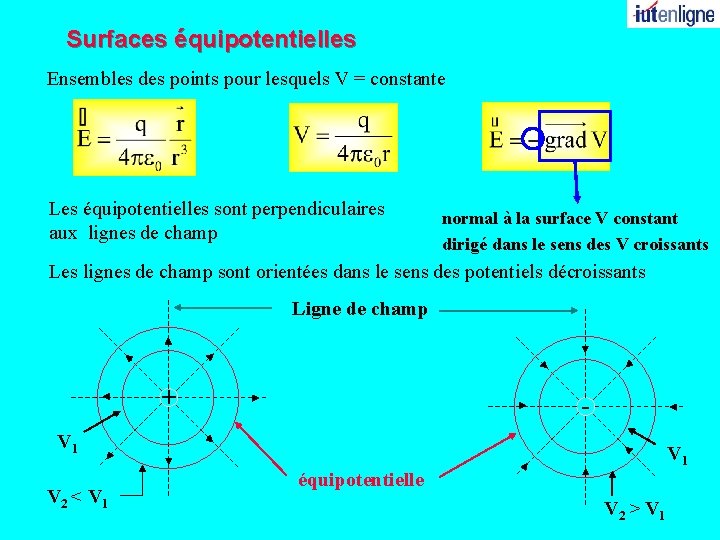
Surfaces équipotentielles Ensembles des points pour lesquels V = constante Les équipotentielles sont perpendiculaires aux lignes de champ normal à la surface V constant dirigé dans le sens des V croissants Les lignes de champ sont orientées dans le sens des potentiels décroissants Ligne de champ + - V 1 V 2 < V 1 équipotentielle V 2 > V 1