1 Gnralits 1 1 Notion de mouvements relatifs

1 - Généralités 1. 1 - Notion de mouvements relatifs Parler de mouvement d’un solide, de vitesse ou de trajectoire d’un point appartenant un solide n’a de sens que si on défini par rapport à quoi on étudie le mouvement. Exemple : On n e peut pas définir la trajectoire du centre de la lune, par contre on sait que la trajectoire du centre de la lune par rapport à la terre se rapproche d’un cercle alors que le trajectoire du centre de la lune par rapport au soleil se rapproche d’une épicyc loïde. 1. 2 - Définitions et notations 1. 2. 1 - Orientation et vitesse de rotation ¾¾® On appelle orientation d’un solide 1 par rapport au solide 2 l’angle entre un axe X 1 fixe dans le ¾¾® solide 1 et un axe X 2 fixe dans le solide 2. On la note q 1/2. On appelle vitesse de rotation du solide 1 par rapport au solide 2 la variation de l’orientation par rapport au temps (C’est la dérivée de l’orientation par rapport au temps). On la note w 1/2 et elle s’exprime en radians par seconde : rad/s ou rad. s 1. On appelle fréquence de rotation du solide 1 par rapport au solide 2 la vitesse de rotation exprimée en t ours par minute : tr/min ou tr. min 1. On la note N 1/2. La relation entre vitesse de rotation et fréquence de rotation est : 2. p. N 1/2 w 1/2 = 60 1. 2. 2 - Trajectoire d’un point On appelle trajectoire d’un point M appartenant au solide 1 par rapport au solide 2 la courbe décrite par les points M au cours du temps dans un repère fixe par rapport au solide 2. On la note TMÎ1/2.

1 - Généralités 1. 2 - Définitions et notations 1. 2. 3 - Position et vitesse d’un point ¾¾® On appelle position d’un point M appartenant au solide 1 par rapport au solide 2, le vecteur O 2 M où O 2 est le centre d’un repère fixe dans le solide 2. On appelle vitesse d’un point M appartenant au solide 1 par rapport au solide 2 la variation de la ¾¾® position de ce point M par rapport au temps. (C’est la dérivée du vecteur O 2 M par rapport au temps). ¾¾¾¾¾® Cette vitesse est donc un vecteur noté : VMÎ1/2 1. 2. 4 - Propriété de la vitesse par rapport à la trajectoire ¾¾¾¾¾® Le vecteur VMÎ1/2 est toujours tangent à la trajectoire T MÎ1/2. 1. 3 - Les différents types de mouvements plan Dans un problème plan, le mouvement d’un solide 1 par rapport à un solide 2 peut être : - Une rotation : Dans ce cas il existe un point O, appelé centre de ¾¾¾¾¾® rotation, appartenant au solide ¾¾® 1 dont la vitesse par rapport au solide 2 est toujours nulle. VOÎ1/2 = 0 - Une translation : Dans ce cas l’orientation du solide 1 par rapport au solide 2 est toujours la w 1/2 = 0 même. q 1/2 = Constante - Un mouvement plan quelconque : Dans ce cas il n’existe pas de point dont la vitesse est toujours nulle et l’orientation du solide 1 par rapport au solide 2 n’est pas constante.

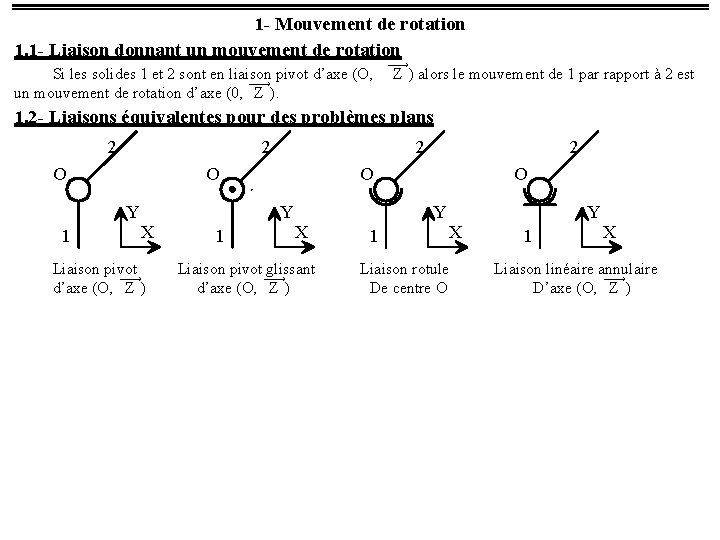
1 - Mouvement de rotation 1. 1 - Liaison donnant un mouvement de rotation Si les solides 1 et 2 sont en liaison pivot d’axe (O, ¾¾® un mouvement de rotation d’axe (0, Z ). ¾¾® Z ) alors le mouvement de 1 par rapport à 2 est 1. 2 - Liaisons équivalentes pour des problèmes plans 2 2 O O Y 1 2 X Liaison pivot ¾¾® d’axe (O, Z ) O Y 1 2 X Liaison pivot ¾¾® glissant d’axe (O, Z ) O Y 1 X Liaison rotule De centre O Y 1 X Liaison linéaire annulaire ¾¾® D’axe (O, Z )

1 - Mouvement de rotation 1. 3 - Caractéristiques d’un mouvement de rotation ¾¾® TMÎ2/1 1 O Soit un solide 2 en rotation d’axe (O, Z ) par rapport à un solide 1, et w 2/1 la vitesse de rotation de 2 par rapport à 1. Alors, on a les caractéristiques suivantes : - La trajectoire de M appartenant à 2 par rapport à 1 : M TMÎ2/1 est un arc de cercle de rayon [OM] 2 - La vitesse de M appartenant à 2 par rapport à 1 : ¾¾¾¾¾® VOÎ2/1 ¾¾¾¾¾® perpendiculaire au rayon [OM] : VMÎ2/1 ¾¾¾¾¾® VMÎ2/1 est ^ [OM] ¾¾¾¾¾® - Le module de la vitesse de M appartenant à 2 par rapport à 1 || VMÎ2/1|| est : ||VMÎ2/1|| = |w 2/1|. R ¾¾¾¾¾® R = OM - La vitesse du centre de rotation est nulle: VOÎ2/1 = 0 où : ¾¾¾¾¾® et w 2/1 en rad. s-1.

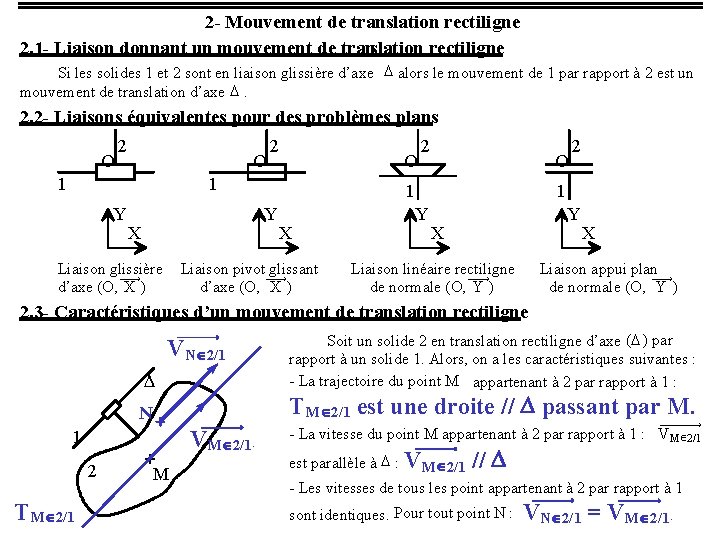
2 - Mouvement de translation rectiligne 2. 1 - Liaison donnant un mouvement de translation rectiligne Si les solides 1 et 2 sont en liaison glissière d’axe D alors le mouvement de 1 par rapport à 2 est un mouvement de translation d’axe D. 2. 2 - Liaisons équivalentes pour des problèmes plans O 2 O 1 Y Y X Liaison glissière ¾¾® d’axe (O, X ) X Liaison pivot ¾¾® glissant d’axe (O, X ) 2 1 Y O 2 1 Y X Liaison linéaire rectiligne ¾¾® de normale (O, Y ) X Liaison appui plan¾¾® de normale (O, Y ) 2. 3 - Caractéristiques d’un mouvement de translation rectiligne ¾¾¾¾¾® VNÎ2/1 D N VMÎ2/1. 2 TMÎ2/1 est une droite // D passant par M. ¾¾¾¾¾® 1 M Soit un solide 2 en translation rectiligne d’axe (D ) par rapport à un solide 1. Alors, on a les caractéristiques suivantes : - La trajectoire du point M appartenant à 2 par rapport à 1 : ¾¾¾¾¾® - La vitesse du point M appartenant à 2 par rapport à 1 : VMÎ2/1 ¾¾¾¾¾® est parallèle à D : VMÎ2/1 // D - Les vitesses de tous les point appartenant à 2 par rapport à 1 sont identiques. Pour tout point N : ¾¾¾¾¾® VNÎ2/1 = VMÎ2/1.

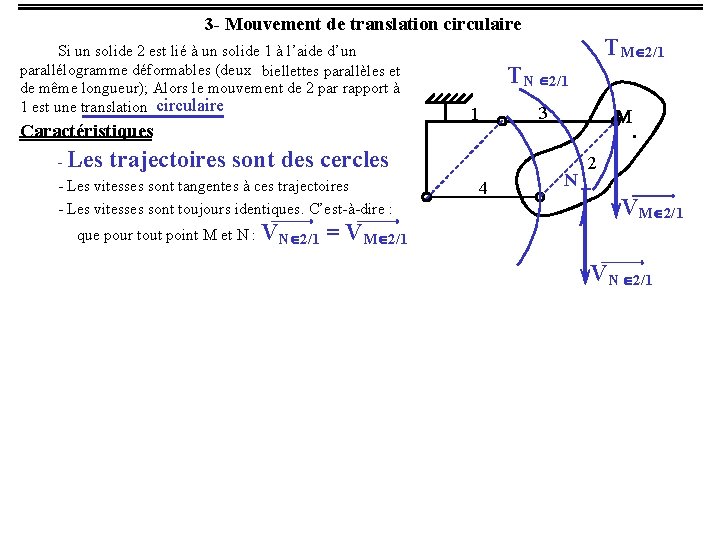
3 - Mouvement de translation circulaire Si un solide 2 est lié à un solide 1 à l’aide d’un parallélogramme déformables (deux biellettes parallèles et de même longueur); Alors le mouvement de 2 par rapport à 1 est une translation circulaire Caractéristiques - Les TN Î2/1 1 trajectoires sont des cercles - Les vitesses sont tangentes à ces trajectoires - Les vitesses sont toujours identiques. C’est-à-dire : ¾¾¾¾¾® que pour tout point M et N : VNÎ2/1 ¾¾¾¾¾® = VMÎ2/1 TMÎ2/1 4 3 N 2 ¾¾¾¾¾® VMÎ2/1 ¾¾¾¾¾® VN Î2/1

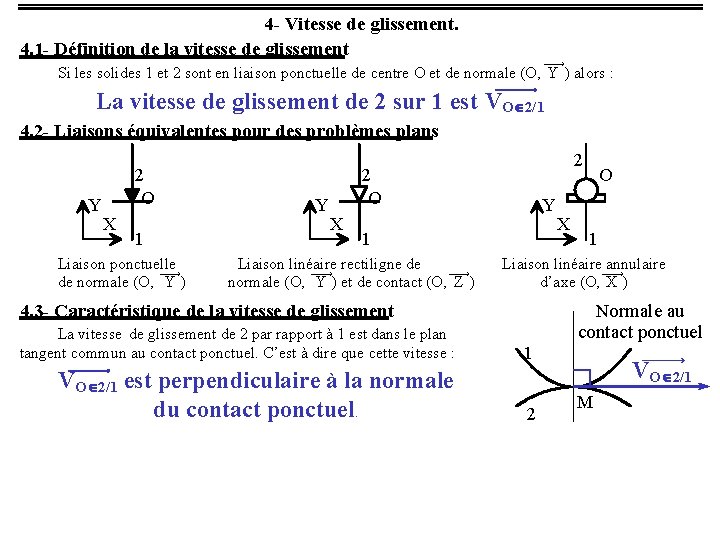
4 - Vitesse de glissement. 4. 1 - Définition de la vitesse de glissement ¾¾® Si les solides 1 et 2 sont en liaison ponctuelle de centre O et de normale (O, Y ) alors : ¾¾¾¾¾® La vitesse de glissement de 2 sur 1 est VOÎ2/1 4. 2 - Liaisons équivalentes pour des problèmes plans Y 2 O X 1 Liaison ponctuelle ¾¾® de normale (O, Y ) Y 2 2 O X Y 1 Liaison linéaire rectiligne de ¾¾® normale (O, Y ) et de contact (O, Z ) 1 Liaison linéaire ¾¾® annulaire d’axe (O, X ) 4. 3 - Caractéristique de la vitesse de glissement La vitesse de glissement de 2 par rapport à 1 est dans le plan tangent commun au contact ponctuel. C’est à dire que cette vitesse : X O Normale au contact ponctuel 1 ¾¾¾¾¾® VOÎ2/1 est perpendiculaire à la normale du contact ponctuel. 2 M

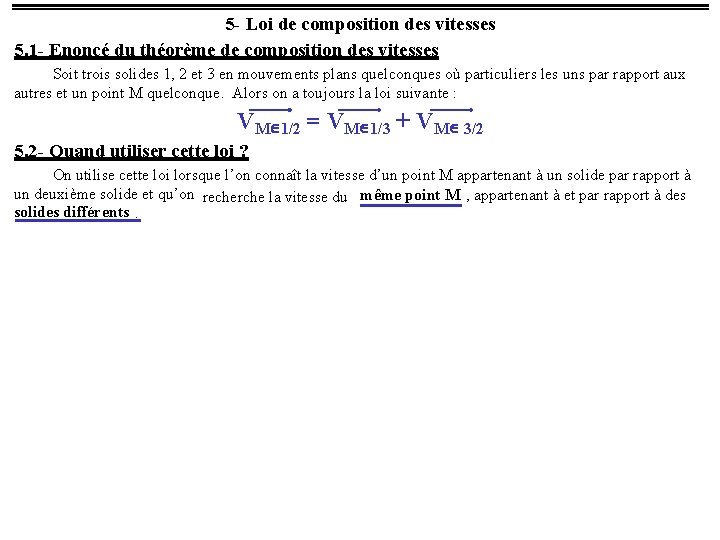
5 - Loi de composition des vitesses 5. 1 - Enoncé du théorème de composition des vitesses Soit trois solides 1, 2 et 3 en mouvements plans quelconques où particuliers les uns par rapport aux autres et un point M quelconque. Alors on a toujours la loi suivante : ¾¾¾¾¾® VMÎ1/2 = VMÎ1/3 + VMÎ 3/2 5. 2 - Quand utiliser cette loi ? On utilise cette loi lorsque l’on connaît la vitesse d’un point M appartenant à un solide par rapport à un deuxième solide et qu’on recherche la vitesse du même point M , appartenant à et par rapport à des solides différents.

6 - Loi d’équiprojectivité des vitesses 6. 1 - Enoncé du théorème d’équiprojectivité Soit deux point M et N quelconques et deux solides 1 et 2 en mouvement plan quelconque ou particulier l’un par rapport à l’autre. Alors ou a toujours la loi suivante : ¾¾¾¾¾® Le projeté orthogonal de VMÎ1/2 sur la droite (MN) est égal au projeté orthogonale de VNÎ1/2 sur la même droite (MN). ¾¾¾¾¾® ¾¾® ¾¾¾¾¾® VMÎ1/2. MN = VNÎ1/2. MN 6. 2 - Quand utiliser cette loi On utilise cette loi lorsque l’on connaît la vitesse d’un point M appartenant à un solide par rapport à un deuxième solide et qu’on recherche la vitesse d’un point différent N, appartenant à et par rapport aux mêmes solides.

7 - Centre instantané de rotation : CIR 7 -1 - Théorème Soit deux solides 1 et 2 en mouvement plan quelconque différent d’une translation , alors à n’importe quel instant du mouvement il existe toujours un point I dont la vitesse est nulle : C’est le Centre Instantané de Rotation (CIR) de 2 par rapport à 1 VIÎ1/2 = 0 On le note : I 2/1 ¾¾¾¾¾® 7 -2 Propriétés du CIR A la date donnée, tout se passe comme si le solide 2 était en rotation de centre I 2/1 par rapport à 1 : - Le CIR est à l’intersection de tous les rayons. Donc si on connaît la direction de deux vitesses de deux points différents alors le CIR est à l’intersection des perpendiculaires à ces directions passant par ces deux points. Cette propriété permet de déterminer le CIR. ¾¾¾¾¾® - Toutes les vitesses ont des directions perpendiculaires aux rayons : VMÎ1/2 ^ (I 2/1 M). Cette propriété permet de déterminer la direction d’une vitesse. Le CIR est un point qui varie au cours du temps sauf si le mouvement d’un solide par rapport à l’autre est un mouvement de rotation. Dans ce cas le CIR est toujours le centre de rotation.