Analysing the Ao A network Project Management Total

Analysing the Ao. A network Project Management

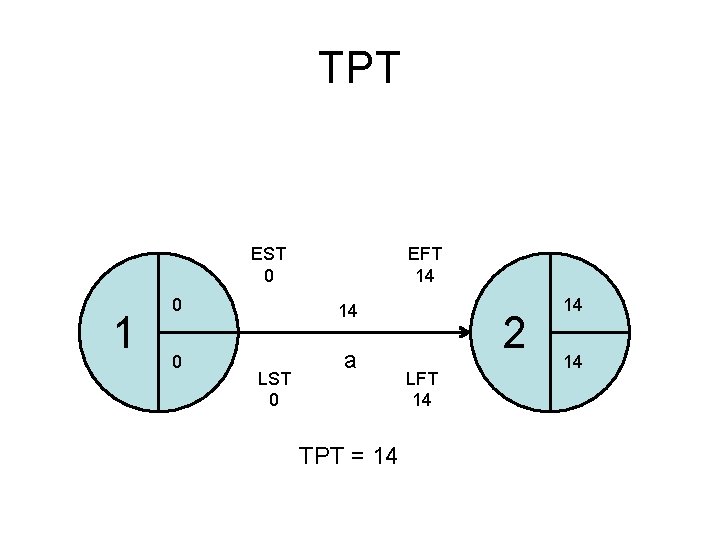
Total Project Time • The minimum time in which the project can be completed. • Calculation: forward pass Forward pass: calculating the earliest event times (EETs) and the earliest start times (ESTs) of all activities. Earliest Finishing Time = EST + Duration

Critical path • Path: continuous series of project activities connected by logical relationships as designated in the project schedule network diagram. • Critical path: sequence of activities that has no float time, and that determines the duration of the project. It is the longest path. Activities on the critical path (or paths) are the critical activities. • The critical path can be identified by a backward pass, calculating the Latest Event Times (LETs) and the Latest Finishing Times (LFTs). • Latest Starting Time = Latest Finishing Time - Duration

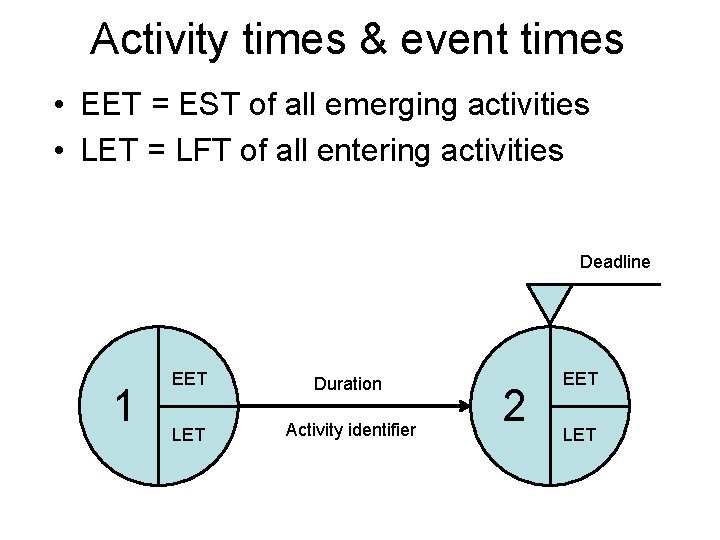
Activity times & event times • EET = EST of all emerging activities • LET = LFT of all entering activities Deadline 1 EET Duration LET Activity identifier 2 EET LET

TPT EST 0 1 EFT 14 0 a LST 0 TPT = 14 2 LFT 14 14 14

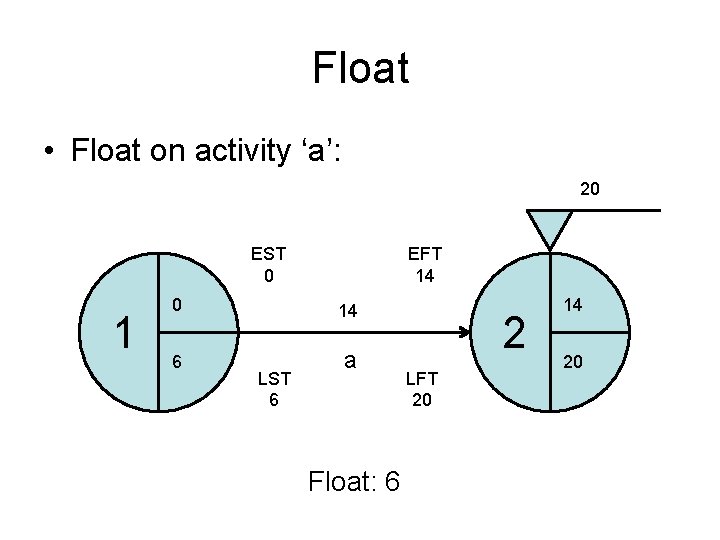
Float • Float on activity ‘a’: 20 EST 0 1 EFT 14 0 14 6 a LST 6 Float: 6 2 LFT 20 14 20

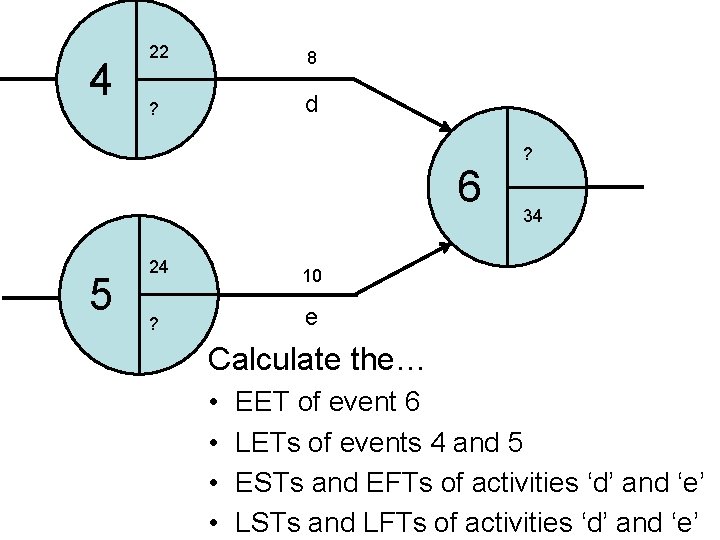
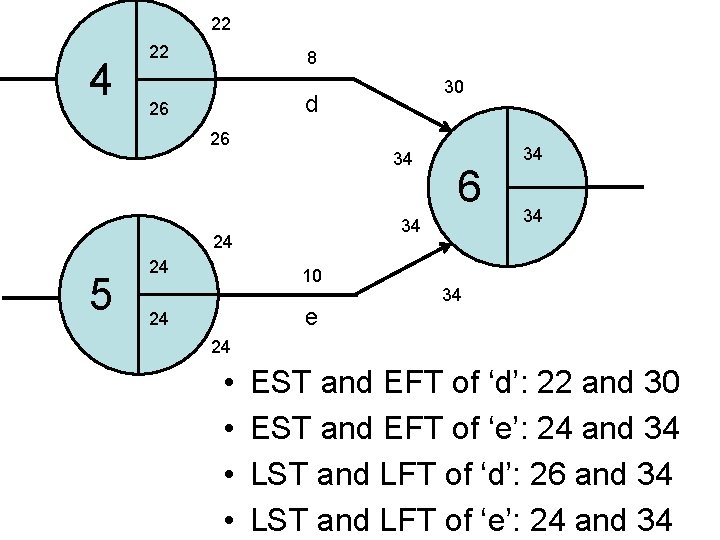
4 22 8 ? d 6 5 24 10 ? e ? 34 Calculate the… • • EET of event 6 LETs of events 4 and 5 ESTs and EFTs of activities ‘d’ and ‘e’ LSTs and LFTs of activities ‘d’ and ‘e’

22 4 22 8 d 26 26 34 24 10 e 24 6 34 24 5 30 34 34 34 24 • • EST and EFT of ‘d’: 22 and 30 EST and EFT of ‘e’: 24 and 34 LST and LFT of ‘d’: 26 and 34 LST and LFT of ‘e’: 24 and 34

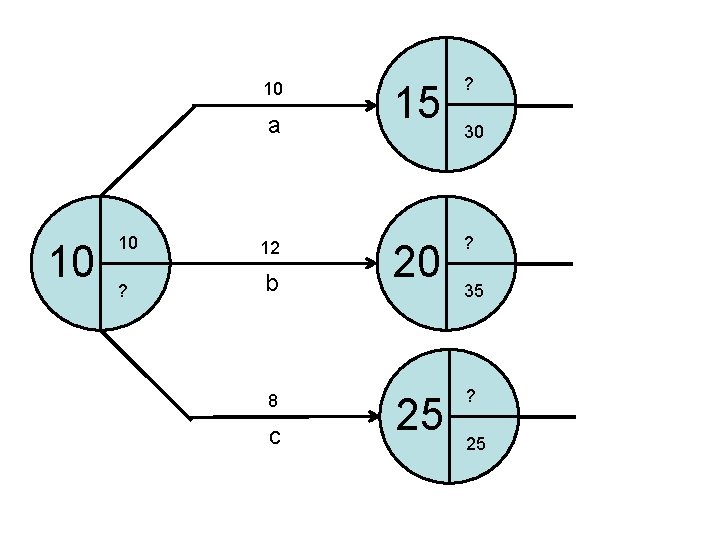
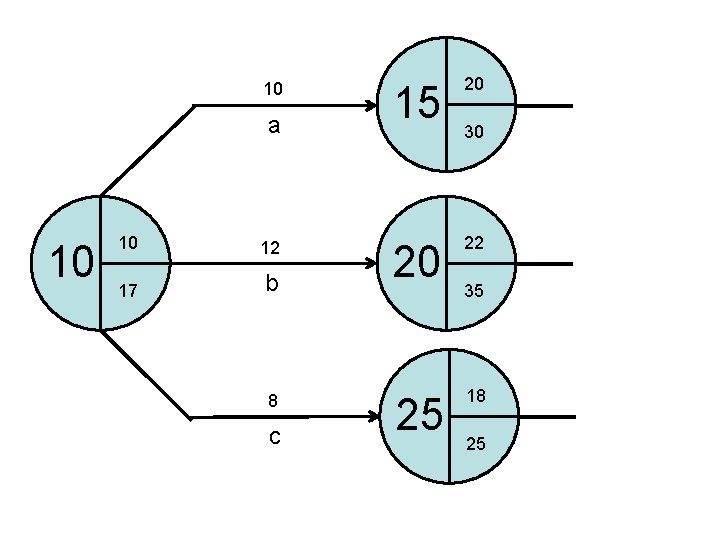
10 a 10 10 12 ? b 8 c 15 ? 20 ? 25 ? 30 35 25

10 a 10 10 12 17 b 8 c 15 20 20 22 25 18 30 35 25

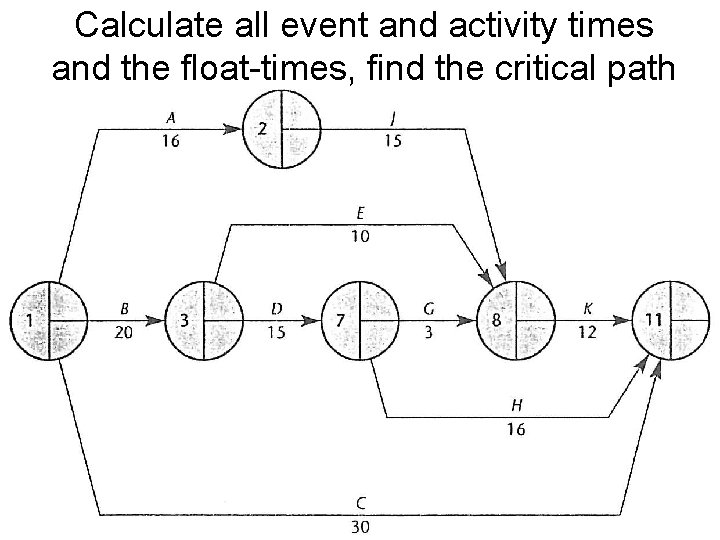
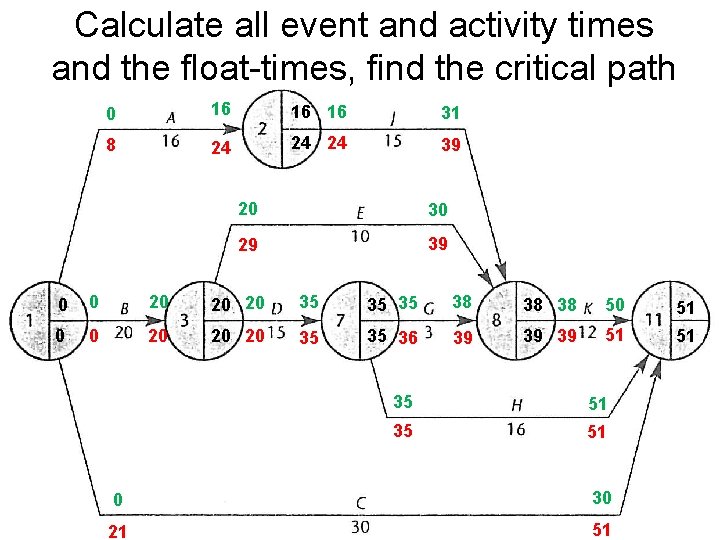
Calculate all event and activity times and the float-times, find the critical path

Calculate all event and activity times and the float-times, find the critical path 0 16 16 16 31 8 24 24 24 39 20 30 29 39 0 0 20 20 20 35 35 35 38 38 38 50 51 0 0 20 20 20 35 35 36 39 39 39 51 51 35 51 0 30 21 51

Activity times and float for the previous diagram Activity A B C D E G H J K EST LST EFT LFT Float

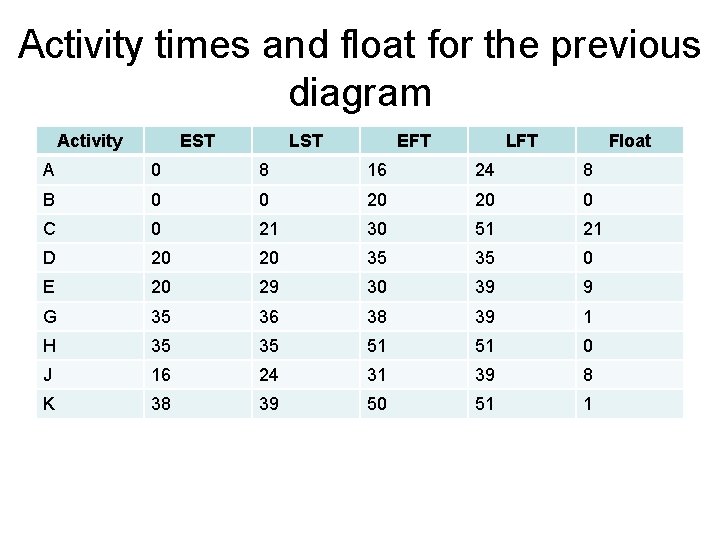
Activity times and float for the previous diagram Activity EST LST EFT LFT Float A 0 8 16 24 8 B 0 0 20 20 0 C 0 21 30 51 21 D 20 20 35 35 0 E 20 29 30 39 9 G 35 36 38 39 1 H 35 35 51 51 0 J 16 24 31 39 8 K 38 39 50 51 1

Four characteristics of the critical path 1. 2. 3. 4. It starts at the first node It is continuous It ends at the last node It has no float

Floats in the Ao. A network

Activity and event times • Activity times: – EST – LST – EFT – LFT • Event times: – EET – LET

Float • Time available for an activity or path in addition to its duration. • It can be positive or negative • It is a property of activities (and available only at given activities) • In case of more succeeding activities, the minimum have to be taken. • Types of float: – Total float – Free float

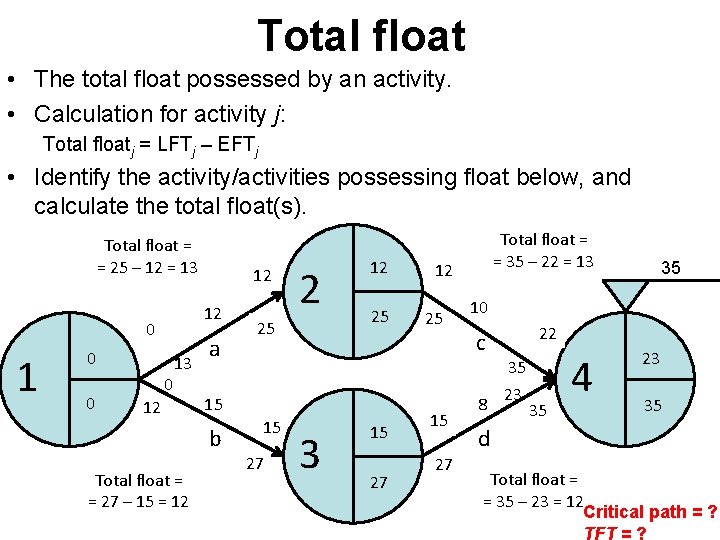
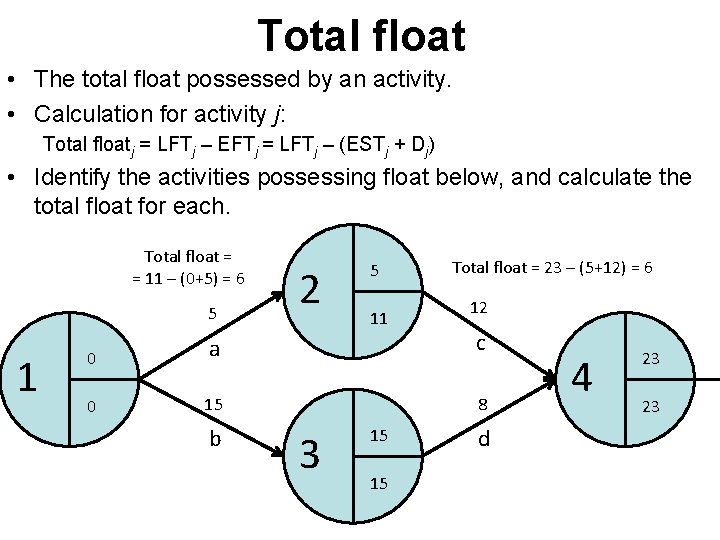
Total float • The total float possessed by an activity. • Calculation for activity j: Total floatj = LFTj – EFTj • Identify the activity/activities possessing float below, and calculate the total float(s). Total float = = 25 – 12 = 13 12 0 1 0 0? 12 0 13 12 a 25 ? 25 15 b Total float = = 27 – 15 = 12 2 ? 12 15 27 3 15 ? 27 ? Total float = = 35 – 22 = 13 12 25 15 27 35 10 c 8 22 35 23 35 4 ? 23 35 d Total float = = 35 – 23 = 12 Critical path = ? TFT = ?

Total float • The total float possessed by an activity. • Calculation for activity j: Total floatj = LFTj – EFTj = LFTj – (ESTj + Dj) • Identify the activities possessing float below, and calculate the total float for each. Total float = = 11 – (0+5) = 6 5 1 2 5 11 Total float = 23 – (5+12) = 6 12 0 a c 0 15 8 b 3 15 15 d 4 23 23

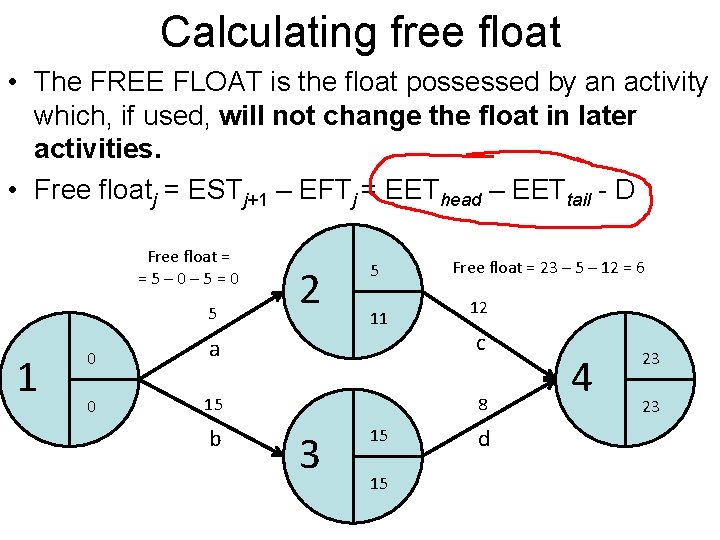
Calculating free float • The FREE FLOAT is the float possessed by an activity which, if used, will not change the float in later activities. • Free floatj = ESTj+1 – EFTj = EEThead – EETtail - D Free float = =5– 0– 5=0 5 1 2 5 11 Free float = 23 – 5 – 12 = 6 12 0 a c 0 15 8 b 3 15 15 d 4 23 23

Positive float on the critical path • If the target time (deadline) for the project (or for a part of the project) is grater than TPT, than a float will appear on the critical path(s), too (and also on other paths). • The float will be the minimal on the critical path(s).

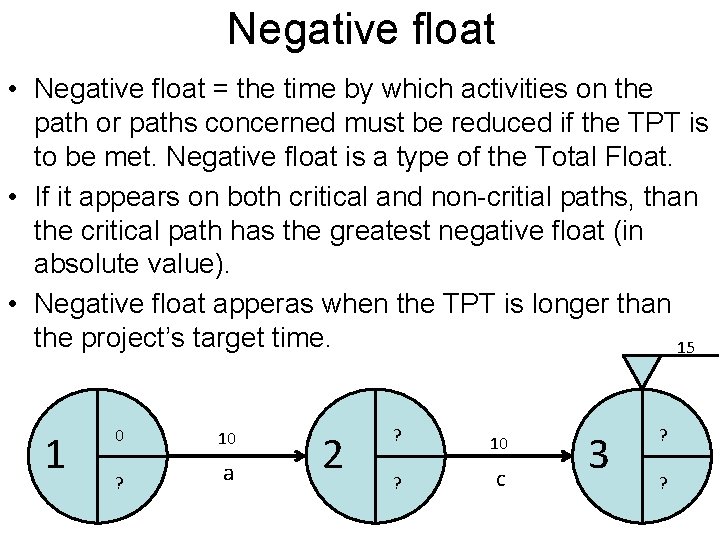
Negative float • Negative float = the time by which activities on the path or paths concerned must be reduced if the TPT is to be met. Negative float is a type of the Total Float. • If it appears on both critical and non-critial paths, than the critical path has the greatest negative float (in absolute value). • Negative float apperas when the TPT is longer than the project’s target time. 15 1 0 10 ? a 2 ? 10 ? c 3 ? ?

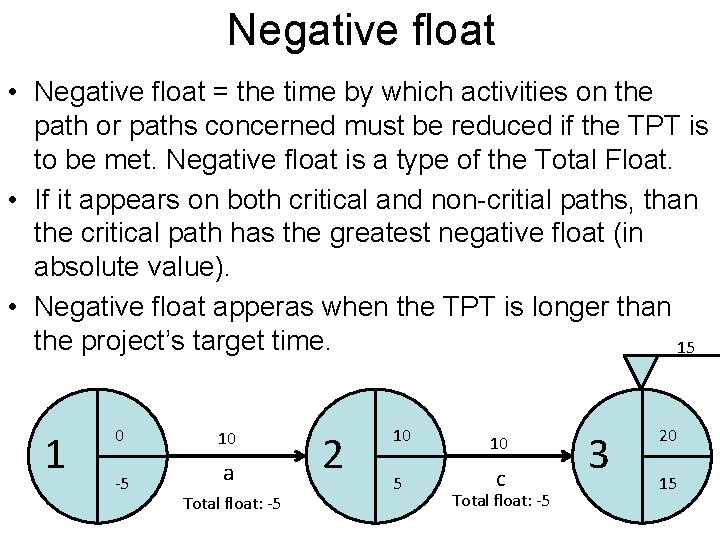
Negative float • Negative float = the time by which activities on the path or paths concerned must be reduced if the TPT is to be met. Negative float is a type of the Total Float. • If it appears on both critical and non-critial paths, than the critical path has the greatest negative float (in absolute value). • Negative float apperas when the TPT is longer than the project’s target time. 15 1 0 10 -5 a Total float: -5 2 10 10 5 c Total float: -5 3 20 15

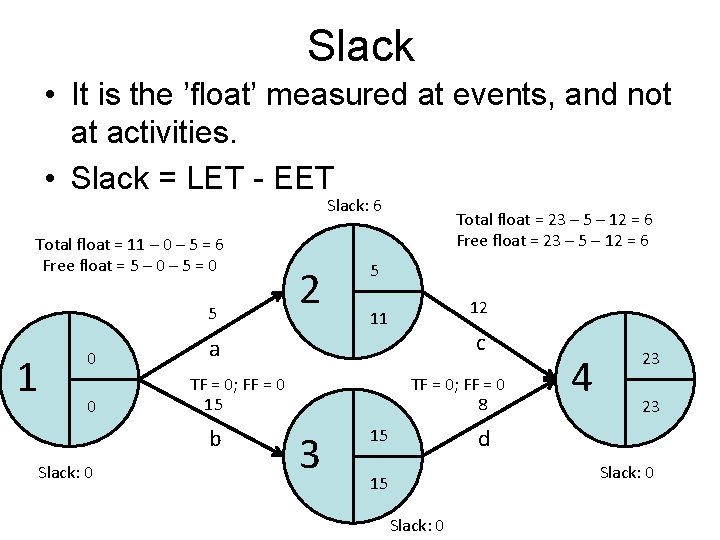
Slack • It is the ’float’ measured at events, and not at activities. • Slack = LET - EET Slack: 6 Total float = 11 – 0 – 5 = 6 Free float = 5 – 0 – 5 = 0 5 1 0 0 5 12 11 c a TF = 0; FF = 0 15 b Slack: 0 2 Total float = 23 – 5 – 12 = 6 Free float = 23 – 5 – 12 = 6 TF = 0; FF = 0 8 3 4 23 23 d 15 Slack: 0

Readings • Lockyer – Gordon (2005) Chapter 13

Thanks for the attention!