Queue Deque and Priority Queue Implementations Chapter 14

Queue, Deque, and Priority Queue Implementations Chapter 14

Chapter Contents l l A Linked List Implementation of a Queue An Array-Based Implementation of a Queue l l A Vector-Based Implementation of a Queue Circular Linked Implementations of a Queue l l l A Circular Array with One Unused Location A Two-Part Circular Linked Chain A Doubly Linked Implementation of a Queue Possible Implementations of a Priority Queue 2

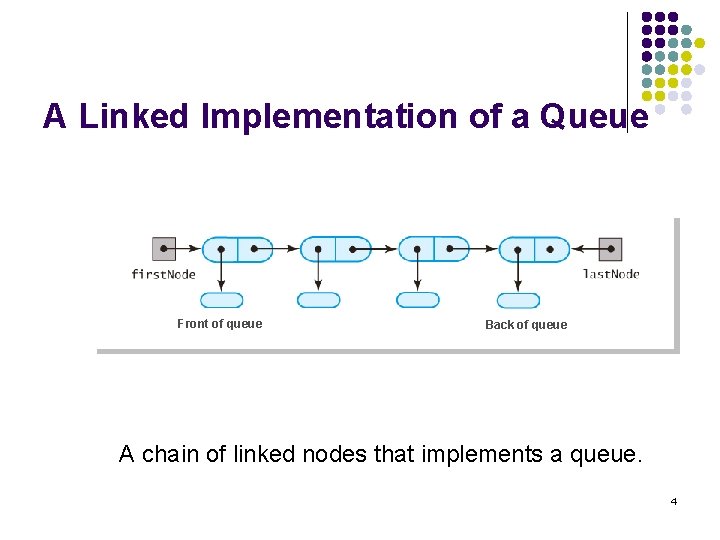
A Linked Implementation of a Queue l Use chain of linked nodes for the queue l l l Two ends at opposite ends of chain Accessing last node inefficient with only head reference Could keep a reference to the tail of the chain With references to both Place front of queue at beginning of chain Place back of queue at end of chain l Remove the head is easy, remove the end requires traverse. 3

A Linked Implementation of a Queue Front of queue Back of queue A chain of linked nodes that implements a queue. 4

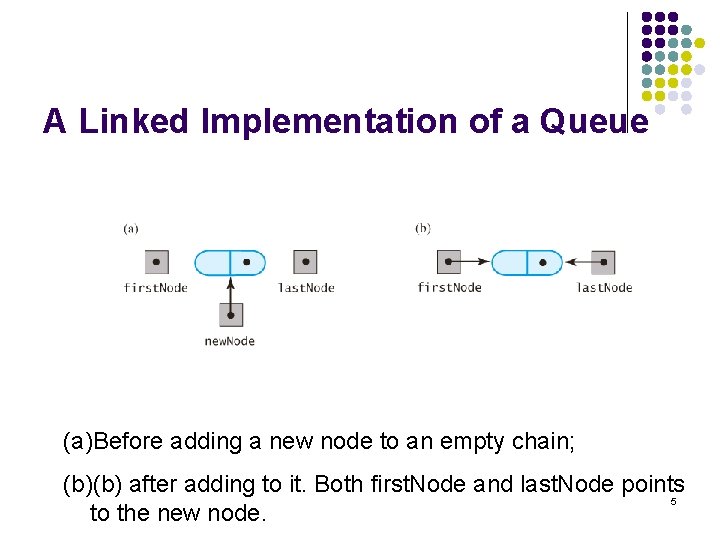
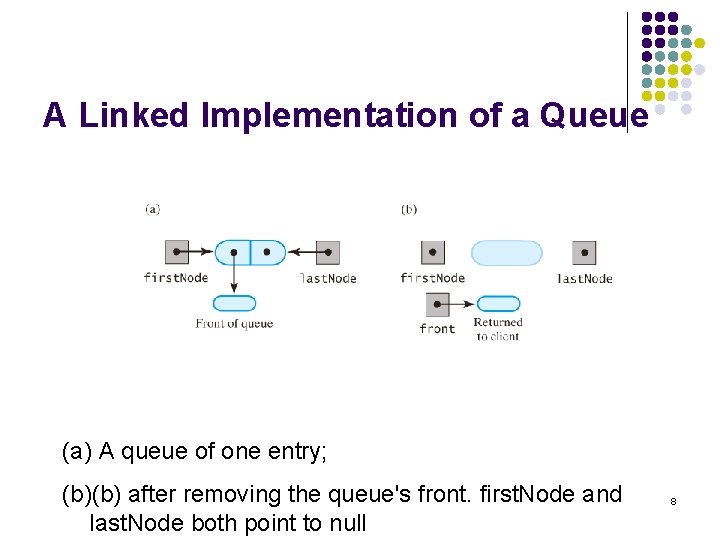
A Linked Implementation of a Queue (a)Before adding a new node to an empty chain; (b)(b) after adding to it. Both first. Node and last. Node points 5 to the new node.

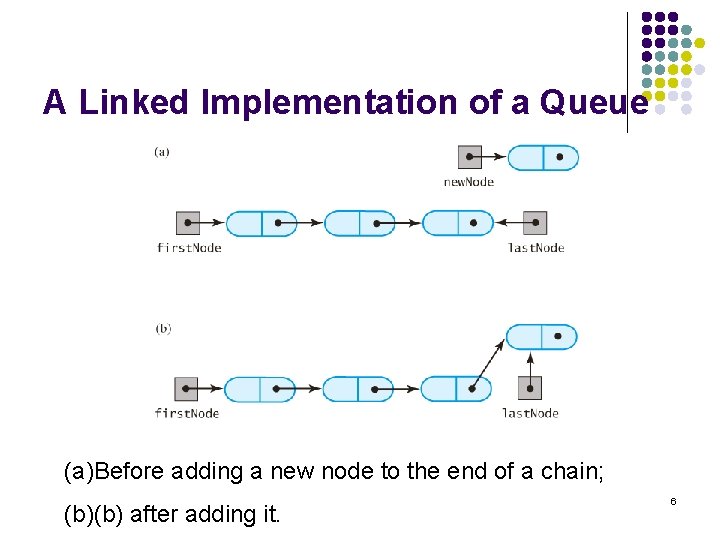
A Linked Implementation of a Queue (a)Before adding a new node to the end of a chain; (b)(b) after adding it. 6

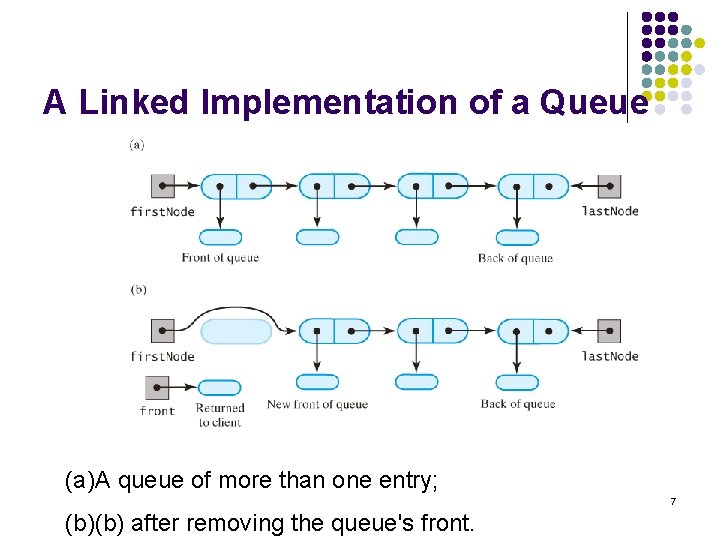
A Linked Implementation of a Queue (a)A queue of more than one entry; 7 (b)(b) after removing the queue's front.

A Linked Implementation of a Queue (a) A queue of one entry; (b)(b) after removing the queue's front. first. Node and last. Node both point to null 8

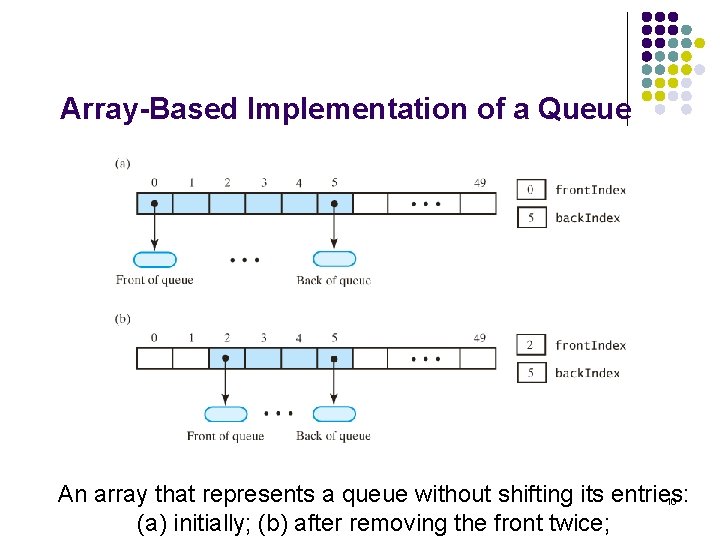
Array-Based Implementation of a Queue l Initially, let queue[0] be the front l front. Index, back. Index are indices of front and back l If we insist queue[0] is front l l Must shift entries when we remove the front Instead, we move front. Index l l Problem then is array can become full But now beginning of array could be empty and available for use 9

Array-Based Implementation of a Queue An array that represents a queue without shifting its entries: 10 (a) initially; (b) after removing the front twice;

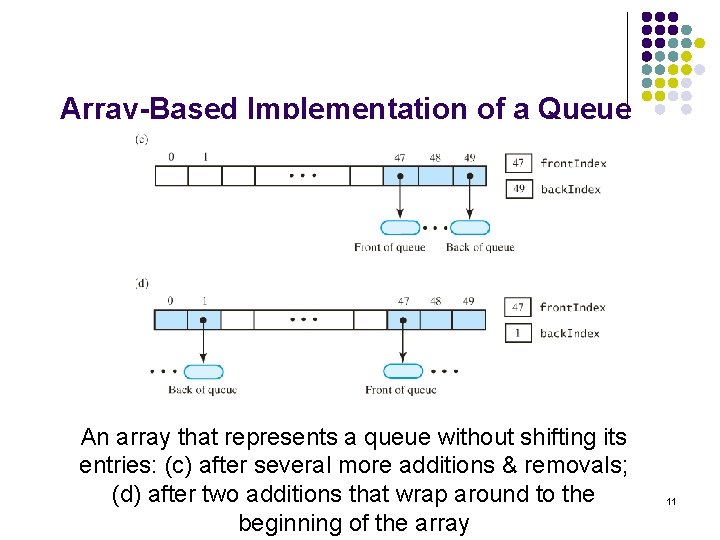
Array-Based Implementation of a Queue An array that represents a queue without shifting its entries: (c) after several more additions & removals; (d) after two additions that wrap around to the beginning of the array 11

A Circular Array l When queue reaches end of array l l Array behaves as though it were circular l l Add subsequent entries to beginning First location follows last one Use modulo arithmetic on indices back. Index = (back. Index + 1) % queue. length 12

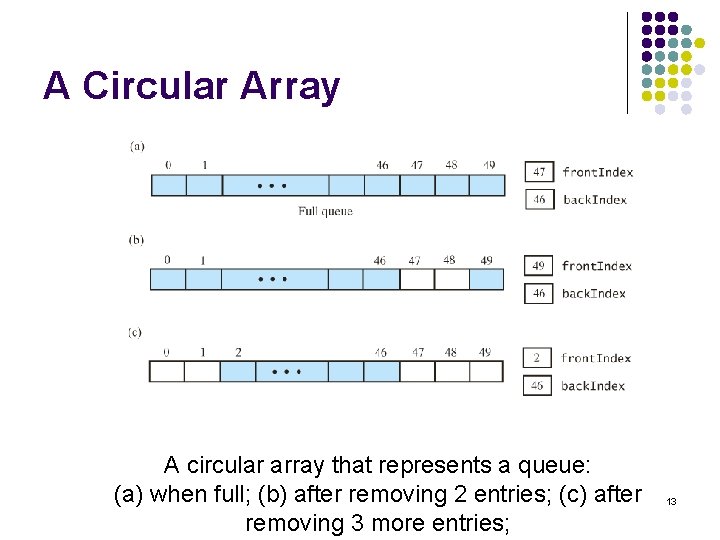
A Circular Array A circular array that represents a queue: (a) when full; (b) after removing 2 entries; (c) after removing 3 more entries; 13

A Circular Array A circular array that represents a queue: (d) after removing all but one entry; (e) after removing remaining entry. Note: with circular array front. Index == back. Index + 1 both when queue is empty and when full 14

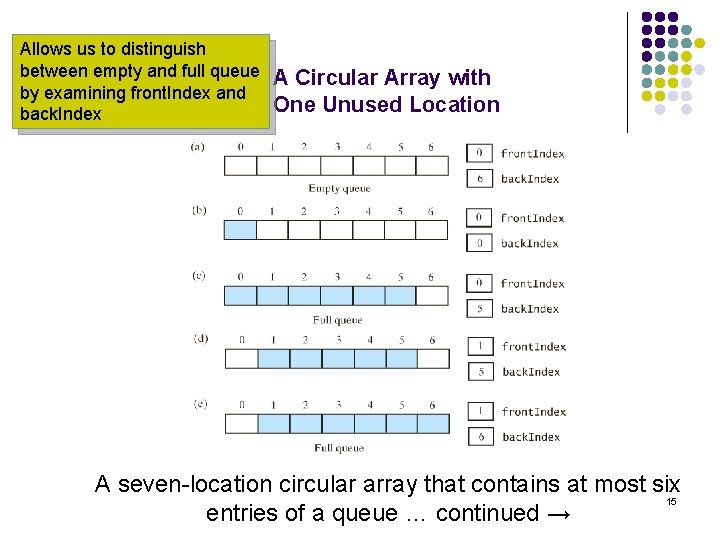
Allows us to distinguish between empty and full queue by examining front. Index and back. Index A Circular Array with One Unused Location A seven-location circular array that contains at most six 15 entries of a queue … continued →

A Circular Array with One Unused Location (ctd. ) A seven-location circular array that contains at most six 16 entries of a queue.

A Circular Array with One Unused Location l l l When the array is full, the index of the unused location is 1 more than back. Index and 1 less than front. Index. The front. Index == (back. Index +2) % queue. length When the array is empty, the front. Index == (back. Index + 1) % queue. length 17

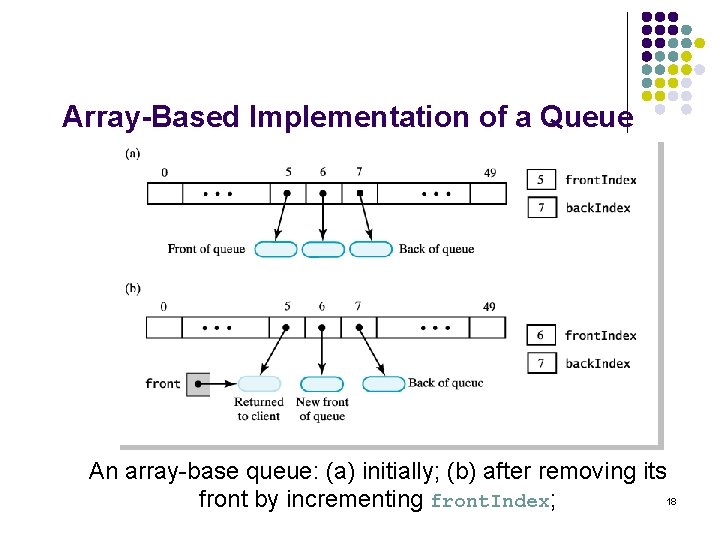
Array-Based Implementation of a Queue An array-base queue: (a) initially; (b) after removing its 18 front by incrementing front. Index;

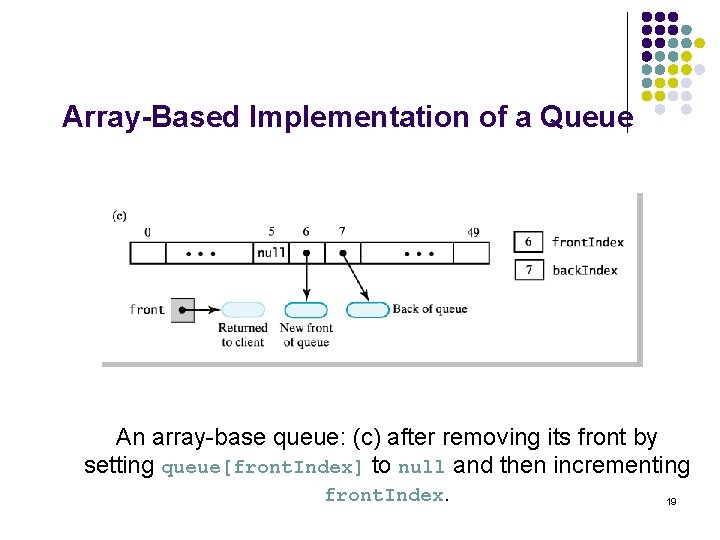
Array-Based Implementation of a Queue An array-base queue: (c) after removing its front by setting queue[front. Index] to null and then incrementing front. Index. 19

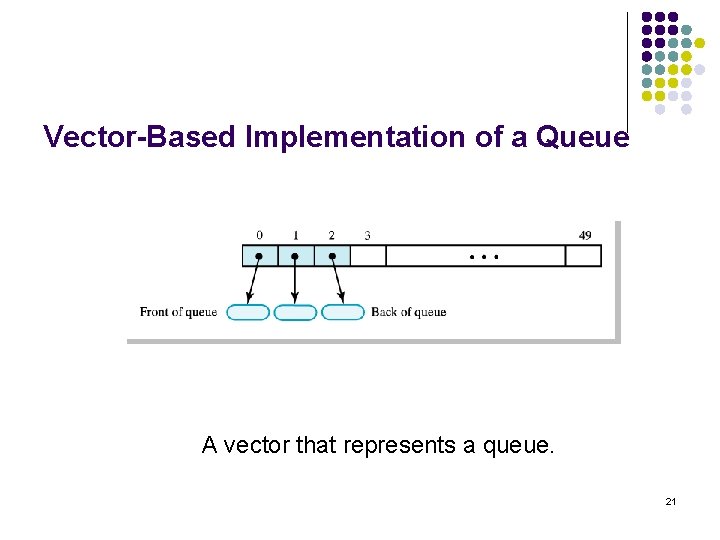
Vector-Based Implementation of a Queue l l Maintain front of queue at beginning of vector Use add. Element(new. Entry) method to add entry at back l l Vector expands as necessary When remove front element remove(0) method, remaining elements move so new front is at beginning of vector l Indexes at front and back not needed 20

Vector-Based Implementation of a Queue A vector that represents a queue. 21

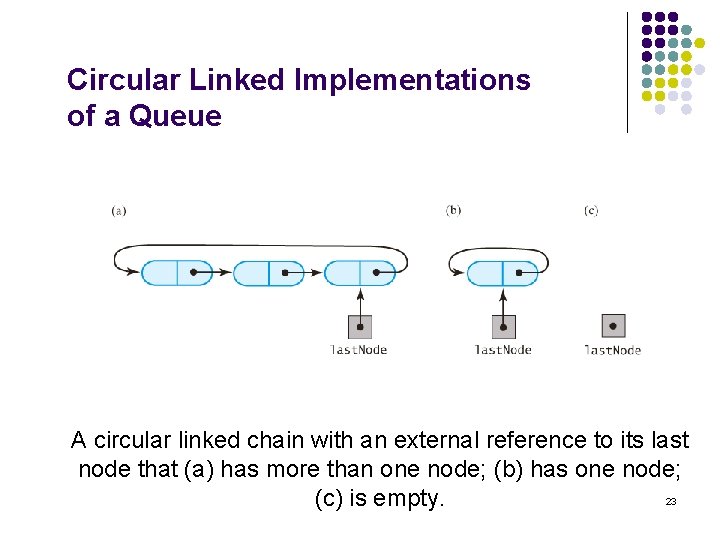
Circular Linked Implementations of a Queue l Last node references first node l l Now we have a single reference to last node And still locate first node quickly by calling last. Node. get. Next. Node() No node contains a null When a class uses circular linked chain for queue l l Only one data item in the class The reference to the chain's last node 22

Circular Linked Implementations of a Queue A circular linked chain with an external reference to its last node that (a) has more than one node; (b) has one node; 23 (c) is empty.

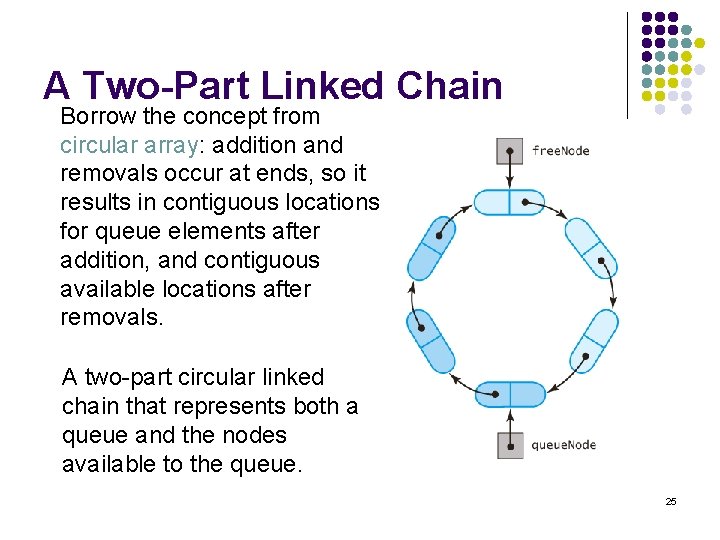
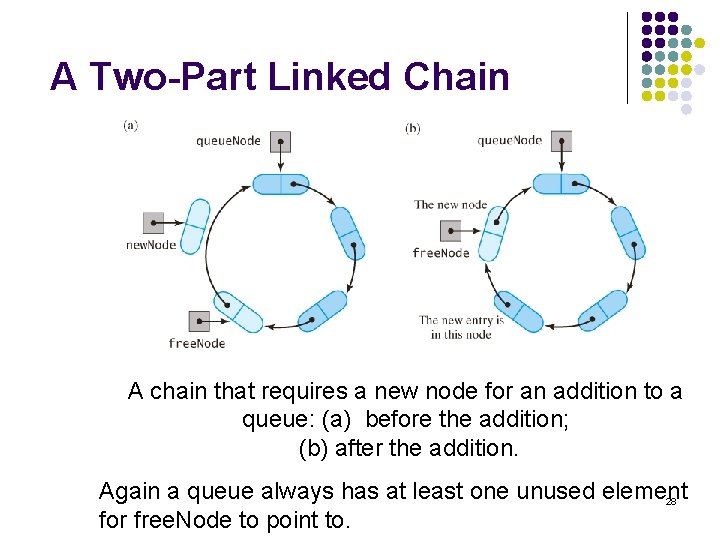
A Two-Part Linked Chain l Linked nodes that form the queue followed by linked nodes available for use in the queue l l l queue. Node references front of queue node free. Node references first available node following end of queue In essence we have two chains l l l One for the queue One for available nodes All joined in a circle 24

A Two-Part Linked Chain Borrow the concept from circular array: addition and removals occur at ends, so it results in contiguous locations for queue elements after addition, and contiguous available locations after removals. A two-part circular linked chain that represents both a queue and the nodes available to the queue. 25

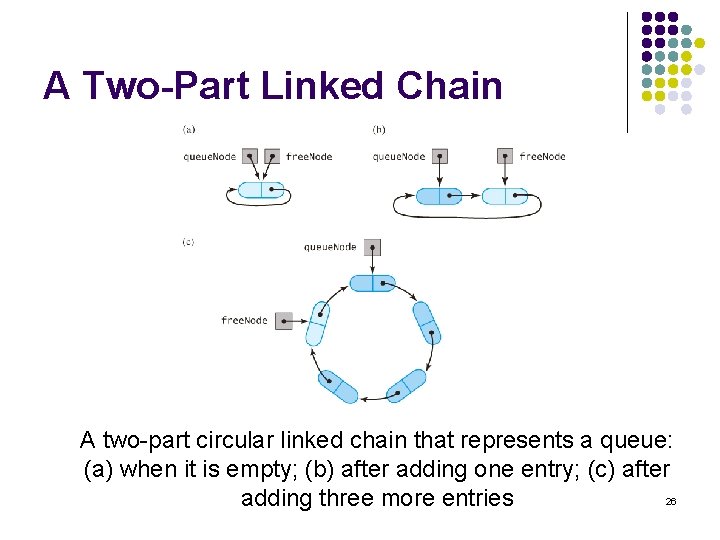
A Two-Part Linked Chain A two-part circular linked chain that represents a queue: (a) when it is empty; (b) after adding one entry; (c) after 26 adding three more entries

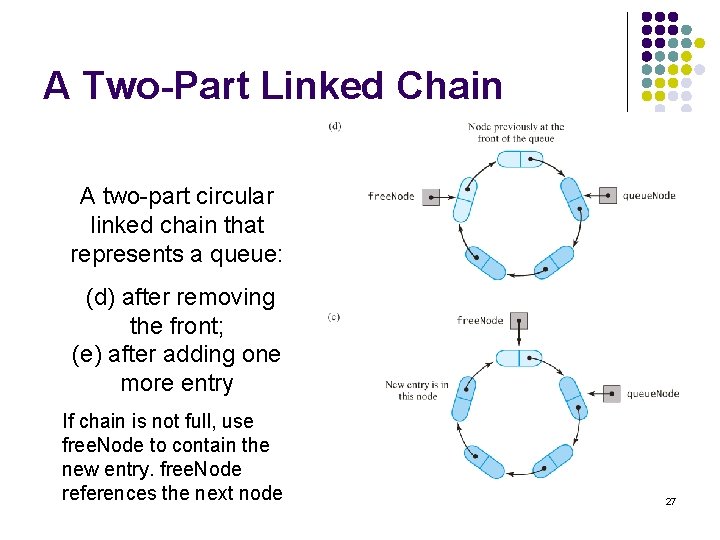
A Two-Part Linked Chain A two-part circular linked chain that represents a queue: (d) after removing the front; (e) after adding one more entry If chain is not full, use free. Node to contain the new entry. free. Node references the next node 27

A Two-Part Linked Chain A chain that requires a new node for an addition to a queue: (a) before the addition; (b) after the addition. Again a queue always has at least one unused element 28 for free. Node to point to.

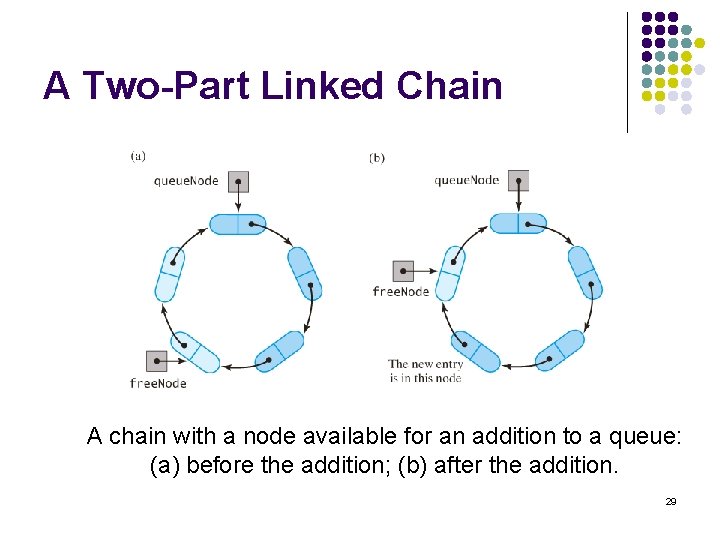
A Two-Part Linked Chain A chain with a node available for an addition to a queue: (a) before the addition; (b) after the addition. 29

Why Two-Part Linked Chain l l The available nodes are not allocated all at once the way locations are allocated for an array. Initially no available nodes; we allocate a node each time we add a new entry. When remove an entry, keep its node in the circle rather than deallocating it for later addition If no available nodes, allocate a new node and link it into the chain. 30

Choosing Linked Implementation l l You can use a linear chain Or you can use a circular chain l l l Both of these implementations requires disconnection and deallocation of a node when removing a node. If, after removing entries from the queue, you seldom add entries, these are fine. But if you frequently add an entry after removing one, the two-part circular chain saves the time of deallocating and reallocating nodes. 31

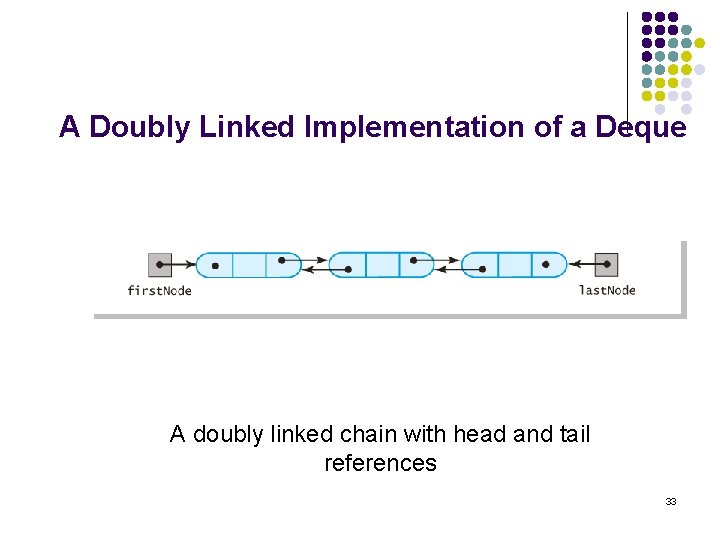
A Doubly Linked Implementation of a Deque l l l Chain with head reference enables reference of first and then the rest of the nodes Tail reference allows reference of last node but not next-to-last We need nodes that can reference both l l l Previous node Next node For remove action to occur at the end of chain, thus the doubly linked chain 32

A Doubly Linked Implementation of a Deque A doubly linked chain with head and tail references 33

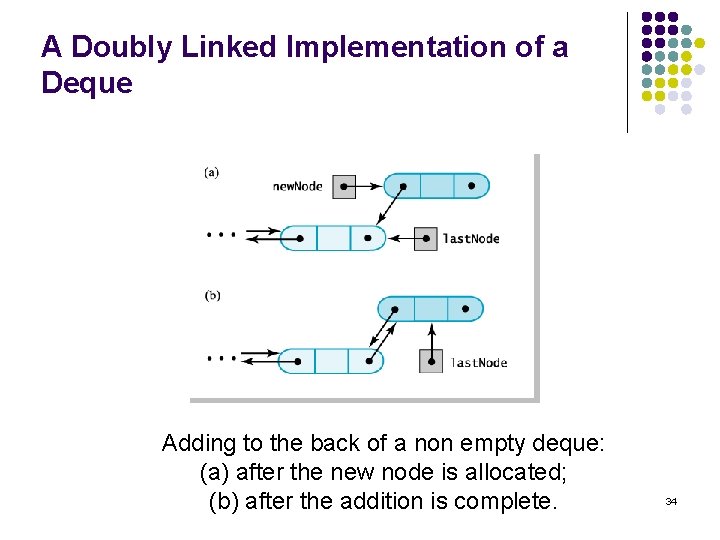
A Doubly Linked Implementation of a Deque Adding to the back of a non empty deque: (a) after the new node is allocated; (b) after the addition is complete. 34

Method Examples: add. To. Back Public void add. To. Back( T new. Entry) { DLNode new. Node = new DLNode(last. Node, new. Entry, null); if( is. Empty()) first. Node = new. Node; else last. Node. set. Next. Node(new. Node); last. Node = new. Node; } 35

remove. Back Method Public T remove. Back() { T back = null; if( !is. Empty()) { back = last. Node. get. Data(); last. Node = last. Node. get. Previous. Node(); if( last. Node == null) first. Node = null; else last. Node. set. Next. Node(null); } return back; } 36

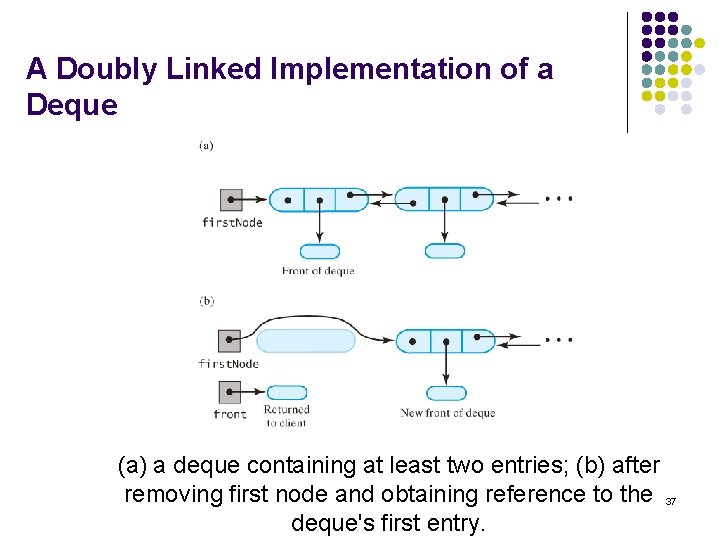
A Doubly Linked Implementation of a Deque (a) a deque containing at least two entries; (b) after removing first node and obtaining reference to the 37 deque's first entry.

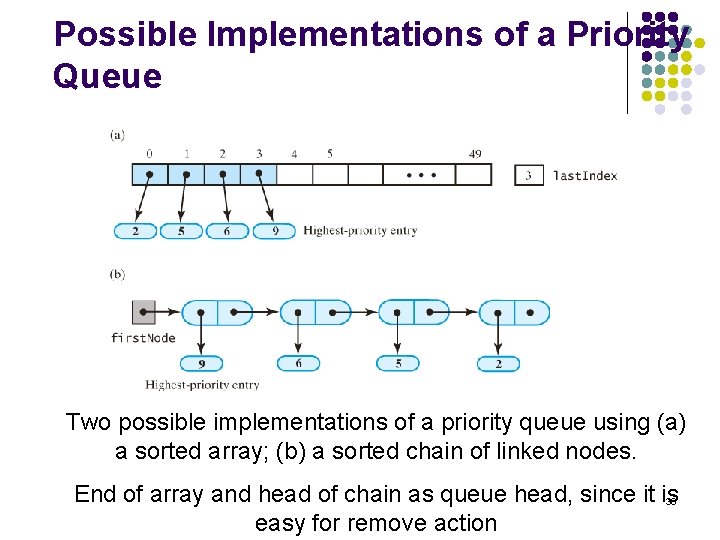
Possible Implementations of a Priority Queue Two possible implementations of a priority queue using (a) a sorted array; (b) a sorted chain of linked nodes. End of array and head of chain as queue head, since it is 38 easy for remove action