Review Array Stack Array List Array Deque and

Review • Array. Stack (Array. List), [Array. Deque, and Dual. Array. Deque] implement the List interface using one or two arrays o get(i), set(i, x) take constant time o add(size(), x), remove(size()-1) [add(0, x), remove(0)] take constant amortized time o Can waste a lot of space − 2/3 of the array positions can be empty o Not suitable for real-time applications − grow(), shrink(), and balance() take O(size()) time.

Coming up • Rootish. Array. Stack: A list implementation with − get(i) and set(i, x) in constant time − add(i, x) and remove(i) in O(1 + size()-i) time − no more than O(size()1/2) wasted space − Suitable for real-time applications o in some languages (not Java) • Dual. Rootish. Array. Deque − A 2 -ended version

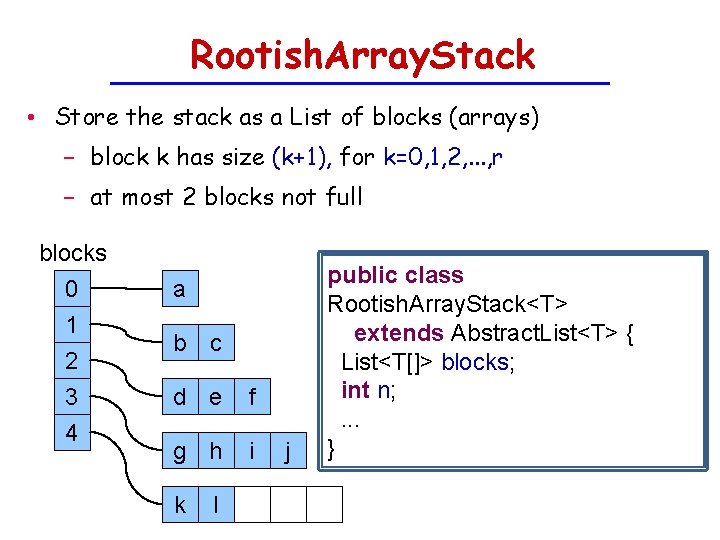
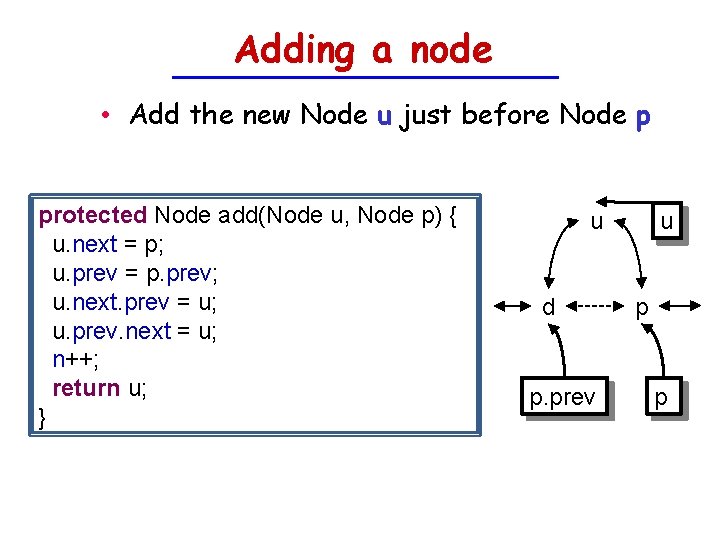
Rootish. Array. Stack • Store the stack as a List of blocks (arrays) − block k has size (k+1), for k=0, 1, 2, . . . , r − at most 2 blocks not full blocks 0 1 2 3 4 a b c d e f g h i k l j public class Rootish. Array. Stack<T> extends Abstract. List<T> { List<T[]> blocks; int n; . . . }

Space analysis • How much space is wasted? − r blocks have room for r(r+1)/2 elements r − To store n elements we need − r(r+1)/2 ≥ n − r ≥ (2 n)1/2 blocks are sufficient r+1 − We only waste O(n 1/2) space keeping track of the blocks • The size of the last 2 blocks is at most 2 r + 3 − Only waste O(n 1/2) space on non-full blocks − Wasted space is only O(n 1/2)

Rootish. Array. Stack – add(i, x) • As usual: − grow() if necessary − shift elements i, . . . , size()-1 right by one position public void add(int i, T x) { int r = blocks. size(); if (r*(r+1)/2 < n + 1) grow(); n++; for (int j = n-1; j > i; j--) set(j, get(j-1)); set(i, x); }

Rootish. Array. Stack – remove(i) • Also as usual: − shift elements i+1, . . . , size()-1 left by one position − shrink() if necessary public T remove(int i) { T x = get(i); for (int j = i; j < n-1; j++) set(j, get(j+1)); n--; shrink(); return x; }

Rootish. Array. Stack – grow() • Add another block of size r − runs in constant time in languages not requiring array initialization − otherwise, takes O(r) = O(size()1/2) time. protected void grow() { blocks. add(f. new. Array(blocks. size()+1)); }

Rootish. Array. Stack – shrink() • Remove blocks until there at most 2 partially empty blocks protected void shrink() { int r = blocks. size(); while (r > 0 && (r-2)*(r-1)/2 >= n) { blocks. remove(blocks. size()-1); r--; } }

Rootish. Array. Stack get(i) and set(i, x) • Find the block index b that contains element i (function i 2 b(i) ) • access element i - b(b+1)/2 within that block public T get(int i) { int b = i 2 b (i); int j = i - b*(b+1)/2; return blocks. get(b)[j]; } public T set(int i, T x) { int b = i 2 b(i); int j = i - b*(b+1)/2; T y = blocks. get(b)[j]; blocks. get(b)[j] = x; return y; }

Rootish. Array. Stack - i 2 b(i) • Converting the List index i into a block number b − 0, . . . , i consists of i+1 elements − Blocks 0, . . . , b can store (b+1)(b+2)/2 elements − We want to find minimum integer b such that o (b+1)(b+2)/2 ≥ i + 1 − Solve (b+1)(b+2)/2 = i + 1 using the quadratic equation − quadratic equation gives a non-integer solution b’ o actually two solutions, but only one is positive − set b = Γb’˥

Rootish. Array. Stack - summary • Theorem: A Rootish. Array. Stack − can perform get(i) and set(i, x) in constant time − can perform add(i, x) and remove(i) in O(1+size()-i) time − uses only O(size()1/2) memory in addition to what is required to store its elements • Key points: − Real-time • no amortization − Low-memory overhead • O(n 1/2) versus O(n) for other array-based stacks

Optimality of Rootish. Array. Stack • Theorem: Any data structure that allows insertions will, at some point during a sequence of n insertions be wasting at least n 1/2 space. • Proof: If the data structure uses more than n 1/2 blocks − Real-time − n 1/2 pointers (references) are being wasted just keeping track of blocks − Otherwise, the data structure uses k ≤ n 1/2 blocks • some block B has size at least n/k ≥ n 1/2 • when B was allocated, it was empty and therefore was a waste of n 1/2 space

Practical Considerations • The use of many arrays to store data means that we can't do shifting with 1 call to System. arraycopy() – Slower than other implementations when i is small • The solution to the quadratic formula in i 2 b(i) requires the square root operation − This can be slow − This can lead to rounding errors • can be corrected by checking that • (b+1)/2 < i ≤ (b+1)(b+2)/2 − Lookup tables can speed things • we only want an integer square root

Dual. Rootish. Array. Deque • Using a Rootish. Array. Stack for the internal stacks within a Dual. Array. Deque we obtain: − Theorem: A Dual. Rootish. Array. Deque • can perform get(i), set(i, x) in constant time • can perform add(i, x) remove(i) in O(1 + min{i, size()-i}) amortized time − uses only O(size()1/2) memory in addition to what is required to store its elements • A real-time version is possible, see − Brodnik, Carlsson, Demaine, Munro, and Sedgewick. Resizeable arrays in optimal time and space. Proceedings of WADS 1999

Review • Array-based implementations of Lists, Queues, Stacks, and Deques have many advantages − Constant-time access by position [get(i), set(i, x)] − Constant-amortized time addition and removal at the ends − Space-efficient versions use only O(n 1/2) extra space • Big disadvantage − Additions and removals in the interior are slow • Running time is at least Ω(min{i, size()-i})

Coming up… • Lists and queues based on (singly and doubly) linked lists – It might use an array of length 2 n to store n elements of data – get(i), set(i, x) are slow add(), remove() with an iterator take constant time • Space-efficient linked lists

Coming up… • Singly-linked lists – Efficient stacks and queues • Doubly-linked lists – Efficient deques • Space-efficient doubly-linked lists – Time/space tradeoff

Singly-linked lists • A list is a sequence of Node: • Node contains – a data value x – a pointer next to the next node in the list protected class Node { T x; Node next; } a b c d e null

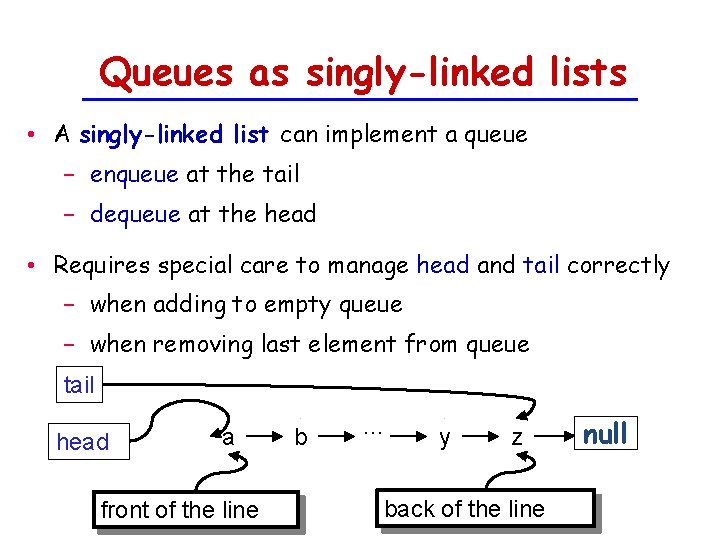
Singly-linked lists (cont'd) • We keep track of the first node in the list (head) • We might also keep track of the last node (tail) public class SLList<T> extends Abstract. Queue<T> { Node head; Node tail; int n; . . . } tail head a b . . . y z null

Queues as singly-linked lists • A singly-linked list can implement a queue − enqueue at the tail − dequeue at the head • Requires special care to manage head and tail correctly − when adding to empty queue − when removing last element from queue tail head a front of the line b . . . y z back of the line null

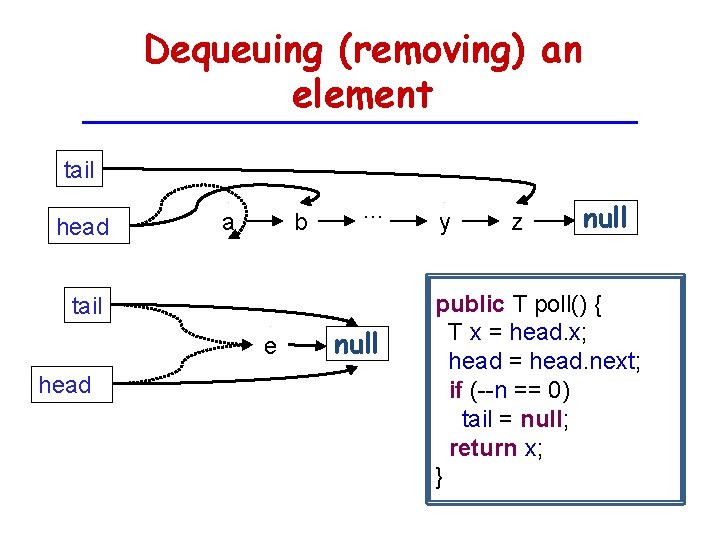
Dequeuing (removing) an element tail head a b . . . tail e head null y z null public T poll() { T x = head. x; head = head. next; if (--n == 0) tail = null; return x; }

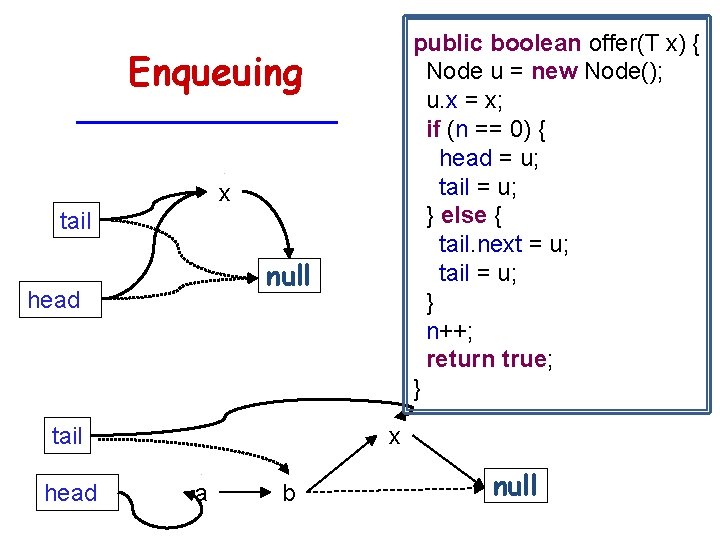
public boolean offer(T x) { Node u = new Node(); u. x = x; if (n == 0) { head = u; tail = u; } else { tail. next = u; tail = u; } n++; return true; } Enqueuing x tail null head tail head x a b null

Delicateness • This code is wrong − can you see why? public boolean offer(T x) { Node u = new Node(); u. x = x; if (n == 0) { head = u; tail = u; } else { tail = u; tail. next = u; } n++; return true; }

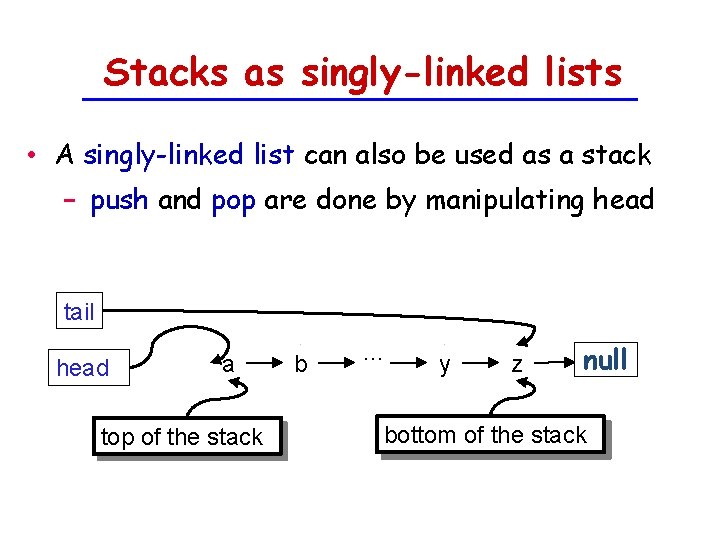
Stacks as singly-linked lists • A singly-linked list can also be used as a stack − push and pop are done by manipulating head tail head a top of the stack b . . . y z null bottom of the stack

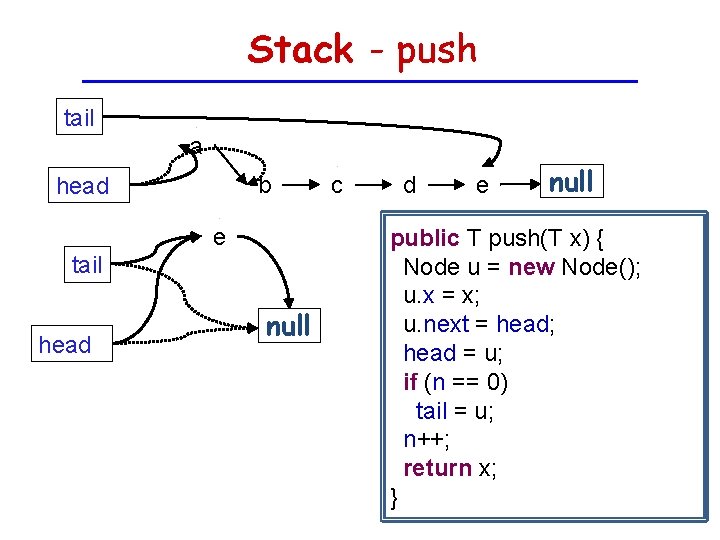
Stack - push tail a b head e tail head null c d e null public T push(T x) { Node u = new Node(); u. x = x; u. next = head; head = u; if (n == 0) tail = u; n++; return x; }

Arbitrary insertion and deletions • In a singly-linked list, we can even do arbitrary insertions/deletions − if we are given a pointer to the preceding element • Getting a pointer to the ith node takes O(i+1) time protected Node get. Node(int i) { Node u = head; for (int j = 0; j < i; j++) u = u. next; return u; } head a b . . . u tail y z null

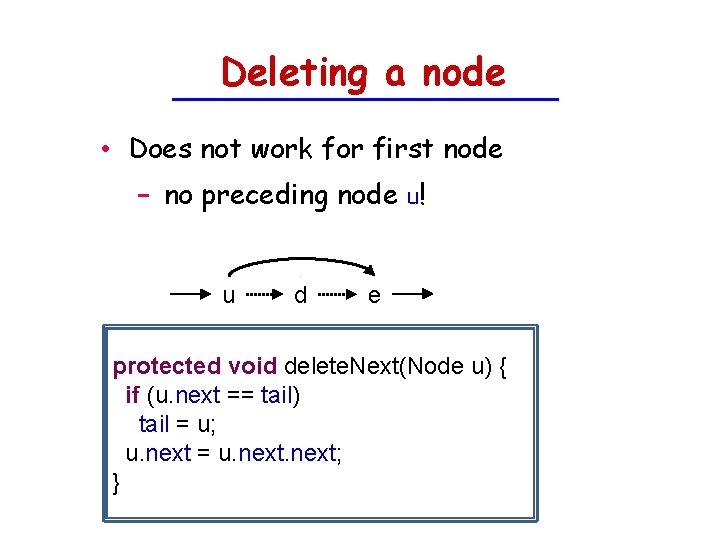
Deleting a node • Does not work for first node − no preceding node u! u d e protected void delete. Next(Node u) { if (u. next == tail) tail = u; u. next = u. next; }

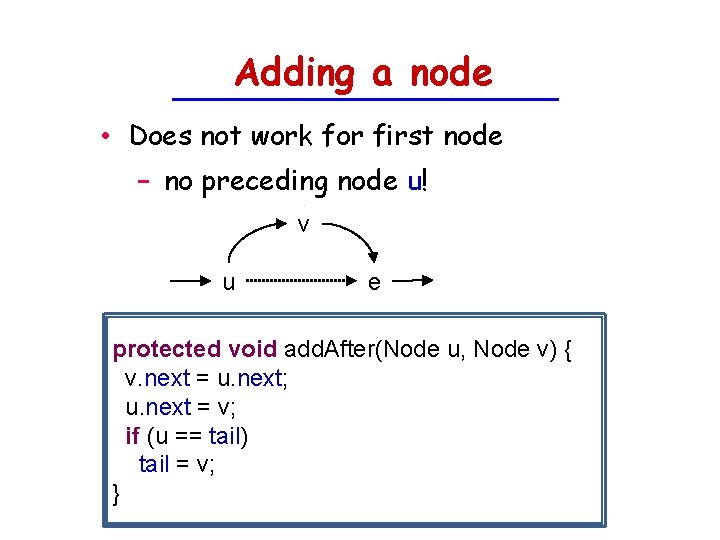
Adding a node • Does not work for first node − no preceding node u! v u e protected void add. After(Node u, Node v) { v. next = u. next; u. next = v; if (u == tail) tail = v; }

In-Class Exercise • Write code for – add(i, x) – remove(i) • Code should run in O(1+i) time 29

Singly-linked list summary • Singly-linked lists support: − push(x), pop(), enqueue(x), dequeue() in constant time (in the worst case) − add(i, x), remove(i) in O(1+i) time • One Node is created per list item − Memory allocation overhead − Node contains data + 1 pointer/reference (next) − At least n pointers for a list of size n

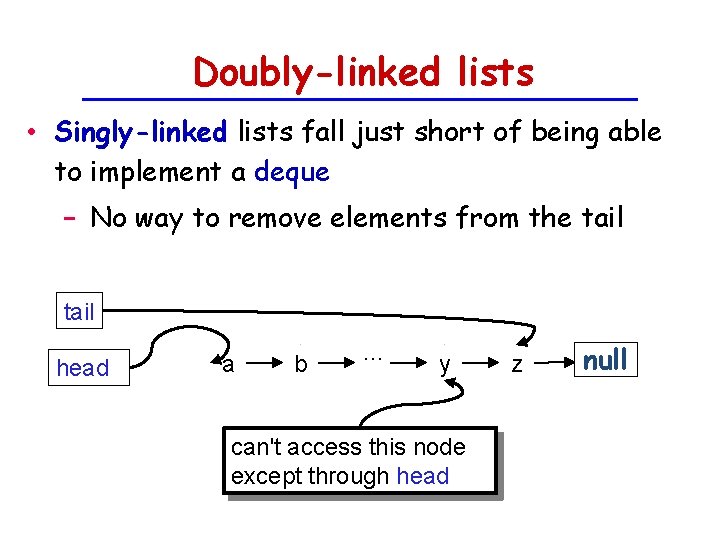
Doubly-linked lists • Singly-linked lists fall just short of being able to implement a deque − No way to remove elements from the tail head a b . . . y can't access this node except through head z null

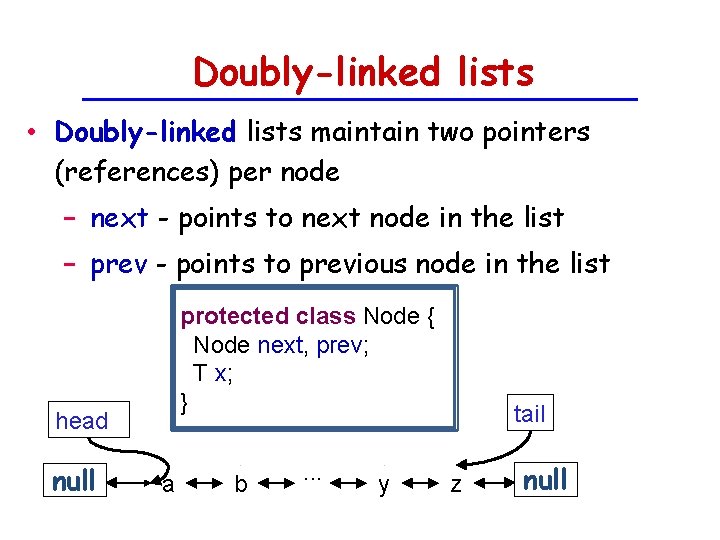
Doubly-linked lists • Doubly-linked lists maintain two pointers (references) per node − next - points to next node in the list − prev - points to previous node in the list protected class Node { Node next, prev; T x; } head null a b . . . y tail z null

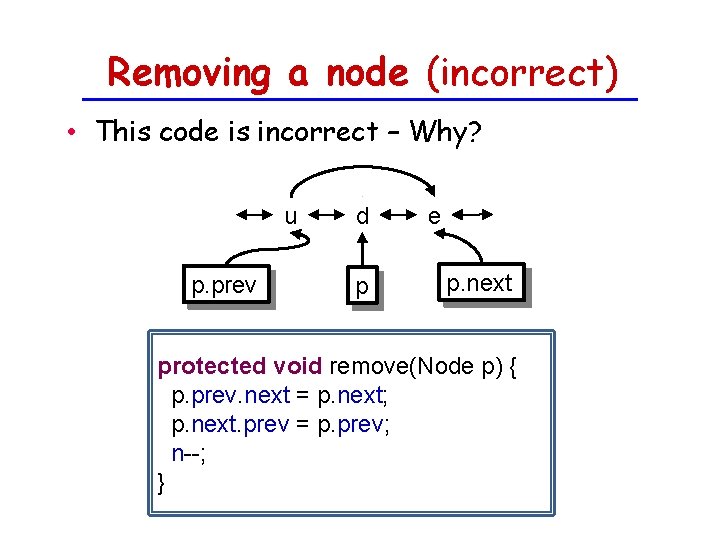
Removing a node (incorrect) • This code is incorrect – Why? u p. prev d p e p. next protected void remove(Node p) { p. prev. next = p. next; p. next. prev = p. prev; n--; }

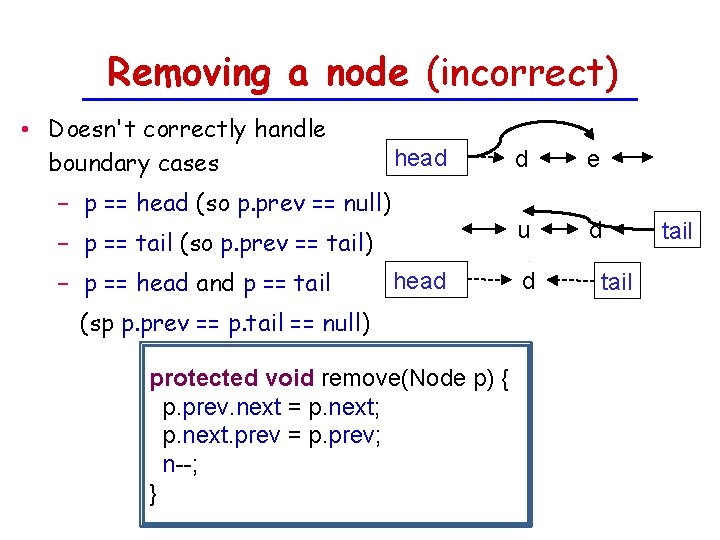
Removing a node (incorrect) • Doesn't correctly handle boundary cases head − p == head (so p. prev == null) − p == tail (so p. prev == tail) − p == head and p == tail head (sp p. prev == p. tail == null) protected void remove(Node p) { p. prev. next = p. next; p. next. prev = p. prev; n--; } d e u d d tail

protected void remove(Node p) { if (p == head && p == tail) { head = null; tail = null; } else if (p == head) { head = p. next; p. next. prev = null; } else if (p == tail) { tail = p. prev; p. prev. next = null; } else { p. prev. next = p. next; p. next. prev = p. prev; } n--; } Versus protected void remove(Node p) { p. prev. next = p. next; p. next. prev = p. prev; n--; }

Code is error prone • Code for boundary cases is troublesome − hard to write correctly − lots of cases − slow to execute (on some architectures) • We would like to get rid of boundary cases − need to get rid of head and tail protected void remove(Node p) { p. prev. next = p. next; p. next. prev = p. prev; n--; }

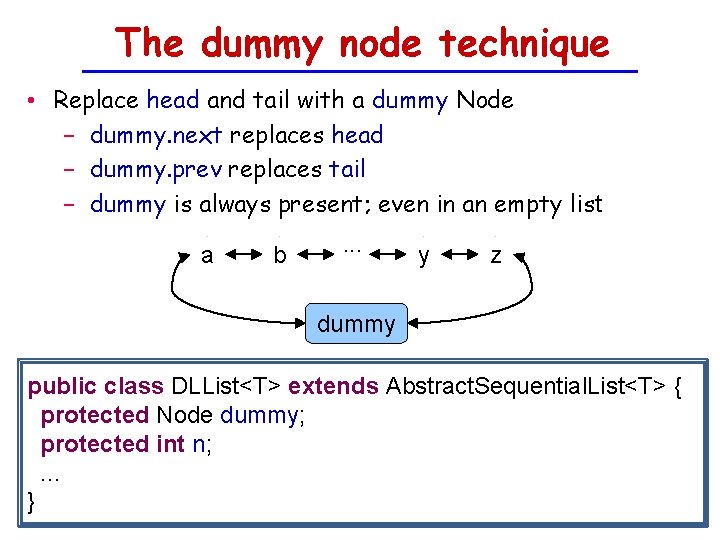
The dummy node technique • Replace head and tail with a dummy Node − dummy. next replaces head − dummy. prev replaces tail − dummy is always present; even in an empty list a b . . . y z dummy public class DLList<T> extends Abstract. Sequential. List<T> { protected Node dummy; protected int n; . . . }

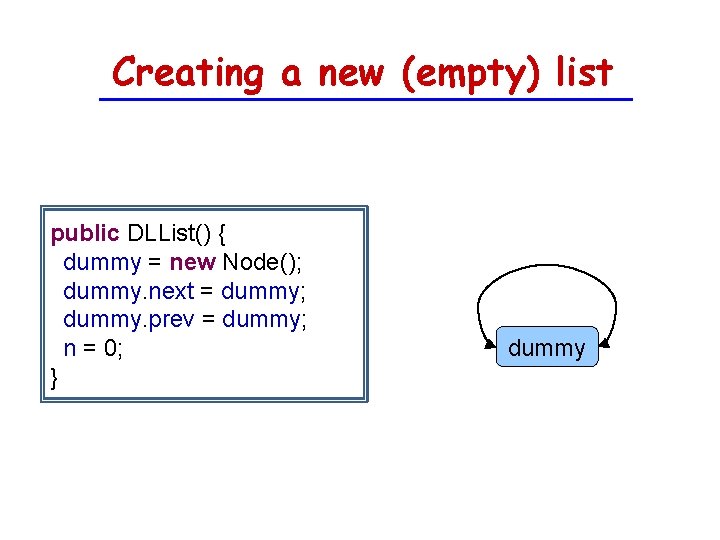
Creating a new (empty) list public DLList() { dummy = new Node(); dummy. next = dummy; dummy. prev = dummy; n = 0; } dummy

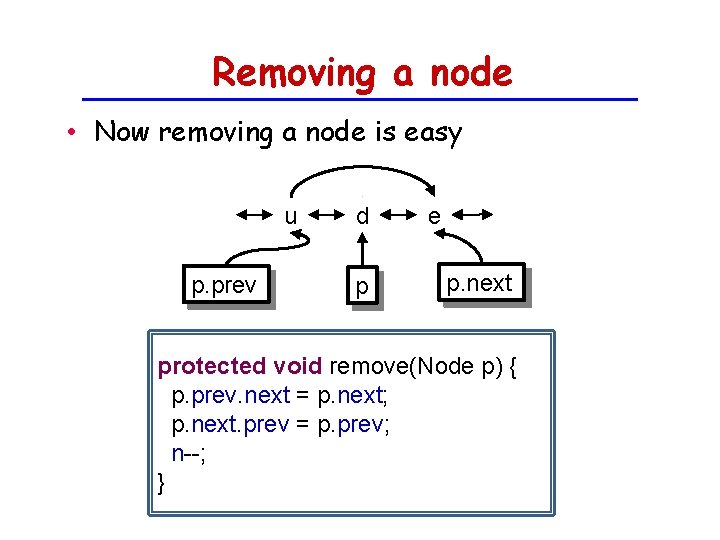
Removing a node • Now removing a node is easy u p. prev d p e p. next protected void remove(Node p) { p. prev. next = p. next; p. next. prev = p. prev; n--; }

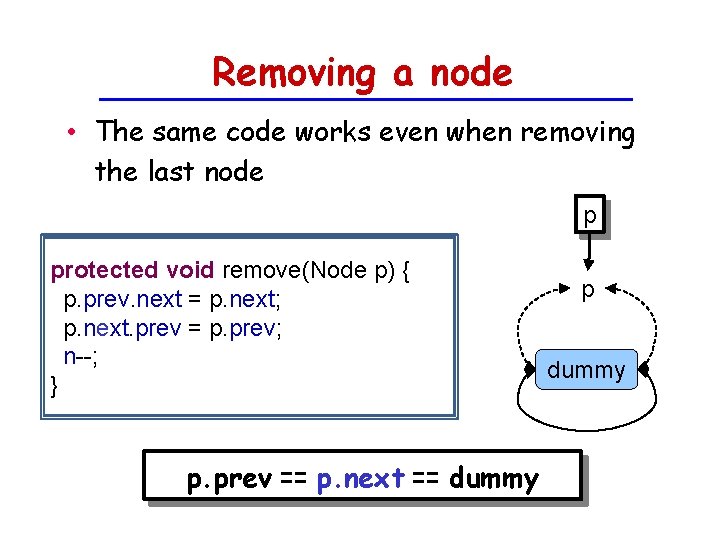
Removing a node • The same code works even when removing the last node p protected void remove(Node p) { p. prev. next = p. next; p. next. prev = p. prev; n--; } p. prev == p. next == dummy p dummy

Adding a node • Add the new Node u just before Node p protected Node add(Node u, Node p) { u. next = p; u. prev = p. prev; u. next. prev = u; u. prev. next = u; n++; return u; } u u d p. prev p p

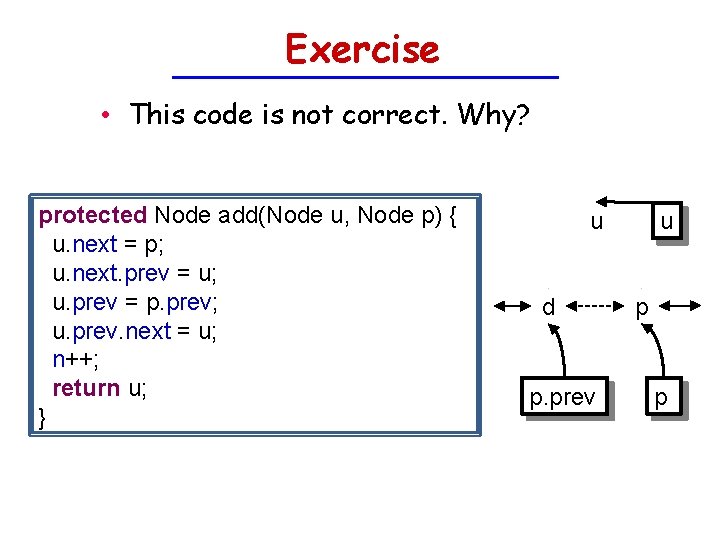
Exercise • This code is not correct. Why? protected Node add(Node u, Node p) { u. next = p; u. next. prev = u; u. prev = p. prev; u. prev. next = u; n++; return u; } u u d p. prev p p

Finding a node • To find the ith node search − from the front if i < size()/2 − from the back otherwise • O(1+min{i, size()-i}) time • Fast − when i~0 (head) − when i~size() (tail) protected Node get. Node(int i) { Node p = null; if (i < n/2) { p = dummy. next; for (int j = 0; j < i; j++) p = p. next; } else { p = dummy; for (int j = n; j > i; j--) p = p. prev; } return(p); }

Removing and Adding • add(i, x) and remove(i) are now easy − Find the appropriate node p − Add x before p (or remove p) • Takes O(1 + min{i, size()-i}) time public void add(int i, T x) { add(get. Node(i), x); } public T remove(int i) { Node p = get. Node(i); remove(p); return p. x; }

Getting and setting • get(i) and set(i, x) are easy too − and take O(1 + min{i, size()-i}) time public T get(int i) { return get. Node(i). x; } public T set(int i, T x) { Node u = get. Node(i); T y = u. x; u. x = x; return y; }

Doubly-linked lists - summary • Doubly-linked lists support − add(i, x), remove(i) in O(1 + min{i, size()-i}) time • deque operations run in constant time per operation − get(i), set(i, x) in O(1+min{i, size()-i}) time − insertion/removal of any node in constant time • given a reference to the node being deleted or • a reference to the node after the insertion

Memory-efficient linked lists • Linked lists are great, except − Each value is stored in its own list node • Each insertion requires allocating a new node • Each node stores 2 pointers − Wasted space is at least 2 × size() × sizeof(pointer) • If data values are small (e. g. , Integer) then wasted space can exceed the space for data

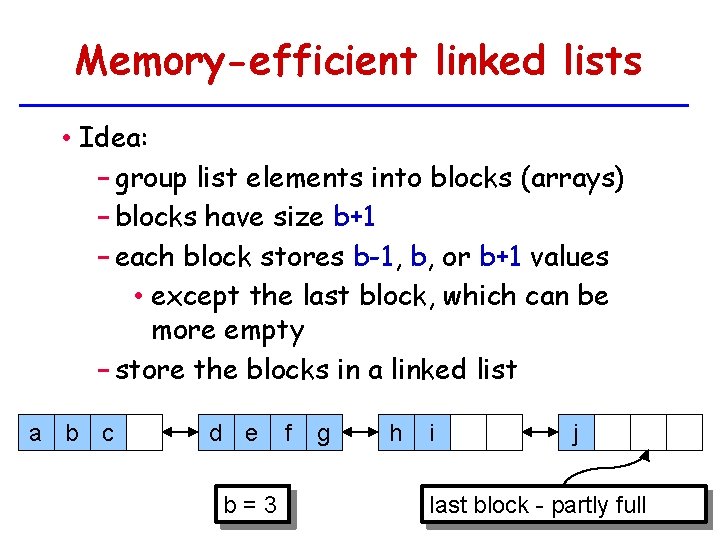
Memory-efficient linked lists • Idea: − group list elements into blocks (arrays) − blocks have size b+1 − each block stores b-1, b, or b+1 values • except the last block, which can be more empty − store the blocks in a linked list a b c d e b=3 f g h i j last block - partly full

Space analysis • The number of blocks is at most − 1 + size()/(b-1) − each block wastes a constant [O(1)] amount of space − wasted space is O(b+n/(b-1)) − By making b larger we can reduce the wasted space • limit is b ~ n 1/2 a b c d e f g h i j

Block data structure • We represent each block as a Bounded. Array. Deque − Array. Deque with size of backing array a set fixed − a. length = b+1 − no grow() or shrink() operations • Sometimes we will want to − move the last element in node u to the front u. next − move the first element in block i to the back of block i-1 − These operations take constant time in a Bounded. Array. Deque

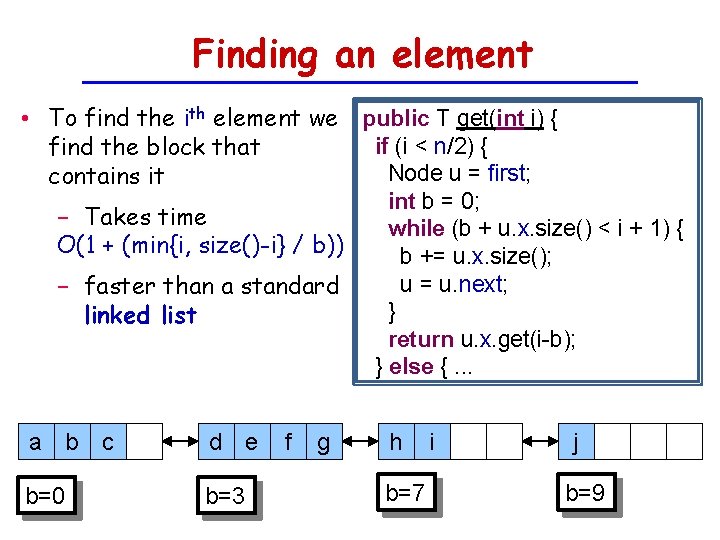
Finding an element • To find the ith element we public T get(int i) { if (i < n/2) { find the block that Node u = first; contains it − Takes time O(1 + (min{i, size()-i} / b)) − faster than a standard linked list a b c d e b=0 b=3 f g int b = 0; while (b + u. x. size() < i + 1) { b += u. x. size(); u = u. next; } return u. x. get(i-b); } else {. . . h b=7 i j b=9

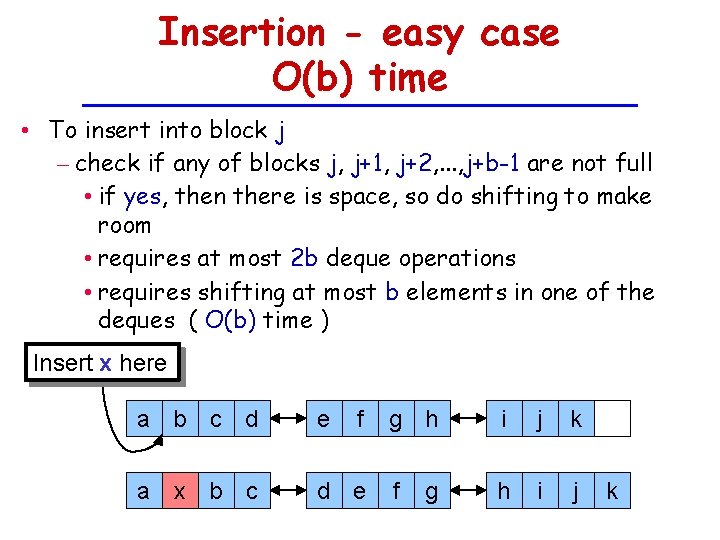
Insertion - easy case O(b) time • To insert into block j – check if any of blocks j, j+1, j+2, . . . , j+b-1 are not full • if yes, then there is space, so do shifting to make room • requires at most 2 b deque operations • requires shifting at most b elements in one of the deques ( O(b) time ) Insert x here a b c d e f a x b c d e g h i j k f h i j g k

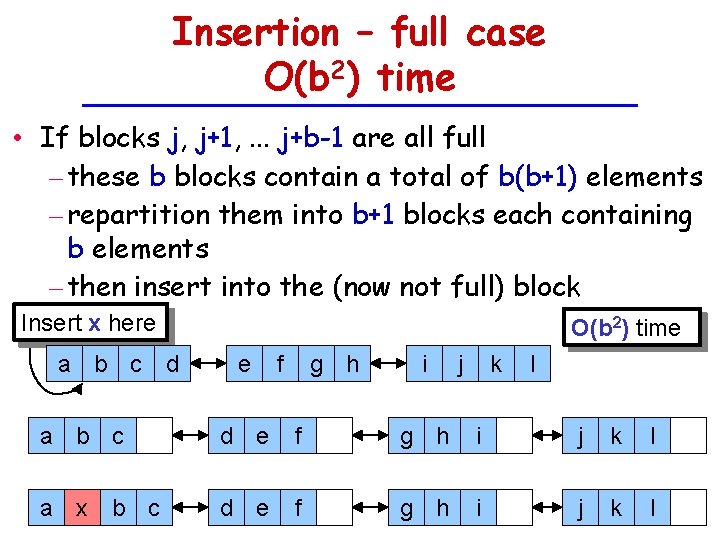
Insertion – full case O(b 2) time • If blocks j, j+1, . . . j+b-1 are all full – these b blocks contain a total of b(b+1) elements – repartition them into b+1 blocks each containing b elements – then insert into the (now not full) block Insert x here a b c d O(b 2) time e f g h i j k l a b c d e f g h i j k l a x b c d e f g h i j k l

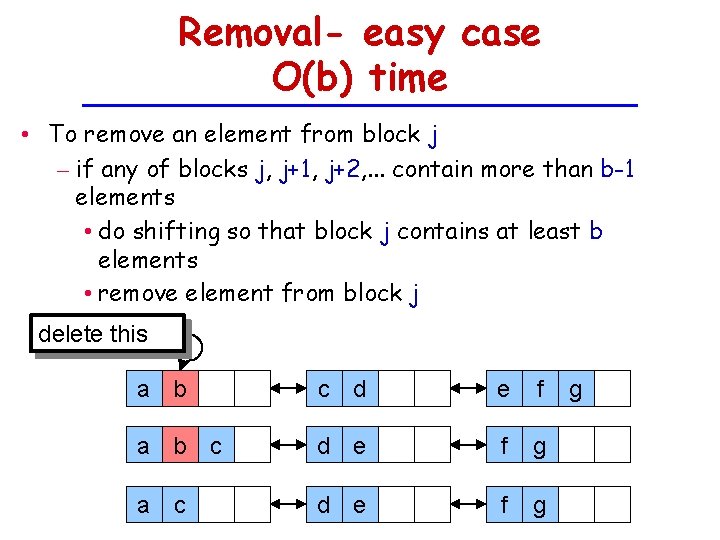
Removal- easy case O(b) time • To remove an element from block j – if any of blocks j, j+1, j+2, . . . contain more than b-1 elements • do shifting so that block j contains at least b elements • remove element from block j delete this a b c d e f g a c d e f g g

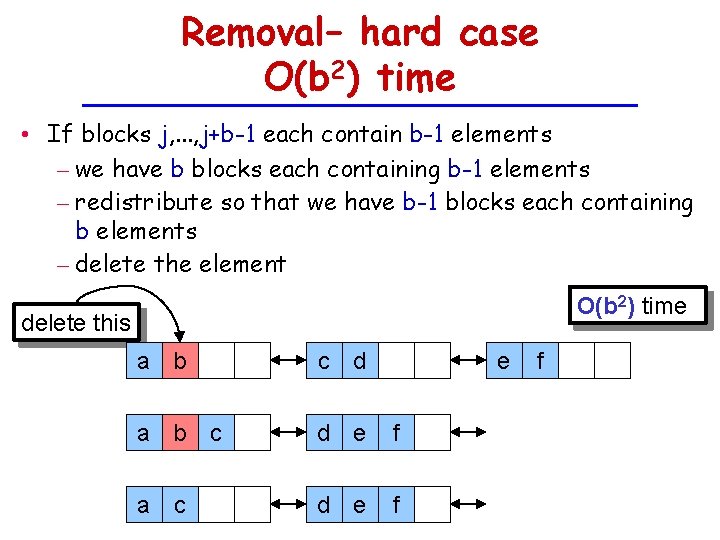
Removal– hard case O(b 2) time • If blocks j, . . . , j+b-1 each contain b-1 elements – we have b blocks each containing b-1 elements – redistribute so that we have b-1 blocks each containing b elements – delete the element O(b 2) time delete this a b c d e f a c d e f f

Space-Efficient Linked List (SElist) • A Compact. DLList has the following properties – wasted space is O(size()/b) – get(i) and set(i, x) each take • O(1 + min{i, size()-i}/b) time – remove(i) and add(i, x) take time • O(b + min{i, size()-i}/b) usually • O(b 2 + min{i, size()-i}/b) occasionally • What do we mean by usually and occasionally?

Amortized analysis of Compact. DLLists • We use a credit scheme – A block with b+1 elements or b-1 elements has 1 credit – A block with b elements has 0 credits • Main idea: – When insertion and removal take b 2 time, we will take away b spare credits – With every insertion and removal we create at most one new credit • Conclusion: At most one out of every b insertion/removals takes b 2 time

Weight-watchers analogy • A hamburger costs 8 credits – [analogous to: operation that takes O(b 2) time] • Every hour of workout gives you one credit – [analagous to: operation that takes O(b) time] • The maximum number of hamburgers you are allowed to eat is – (# hours spent working out)/8

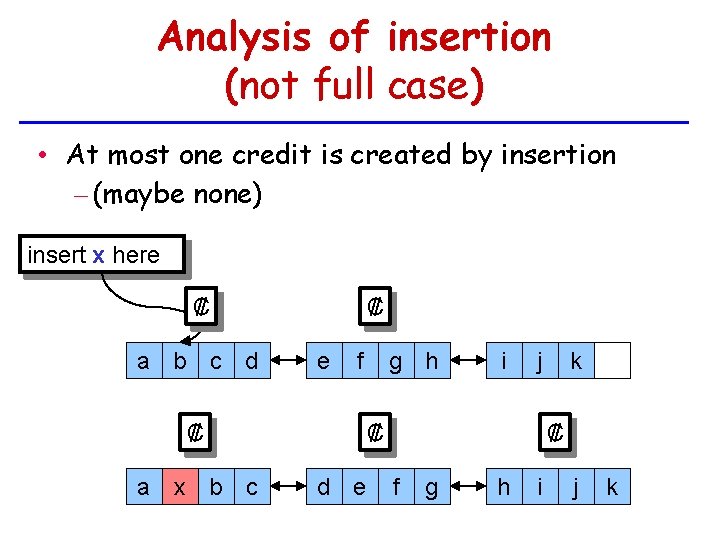
Analysis of insertion (not full case) • At most one credit is created by insertion – (maybe none) insert x here ₡ a b c d ₡ e f ₡ a x b c g h i j ₡ d e k ₡ f g h i j k

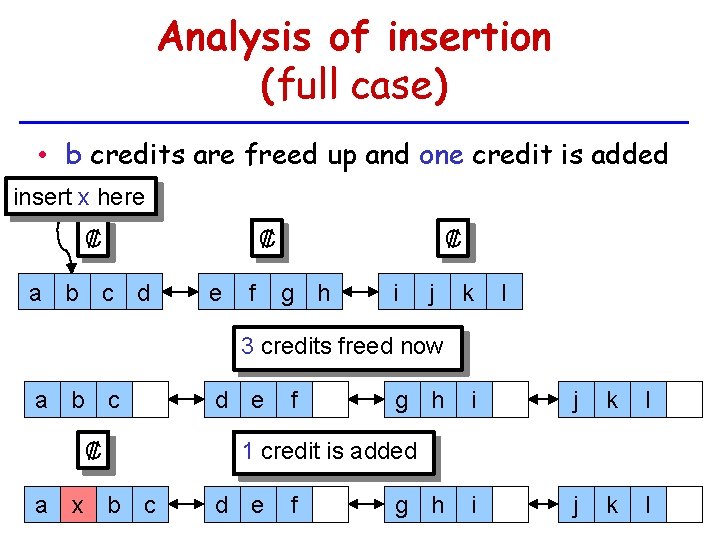
Analysis of insertion (full case) • b credits are freed up and one credit is added insert x here ₡ a b c d ₡ e f ₡ g h i j k l 3 credits freed now a b c ₡ a x b c d e f g h i j k l 1 credit is added d e f g h

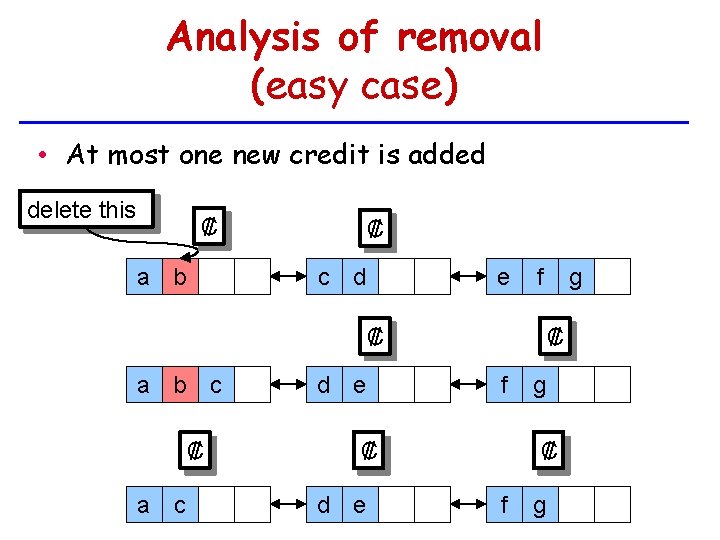
Analysis of removal (easy case) • At most one new credit is added delete this ₡ a b ₡ c d e f ₡ a b c ₡ a c d e ₡ f ₡ d e g g ₡ f g

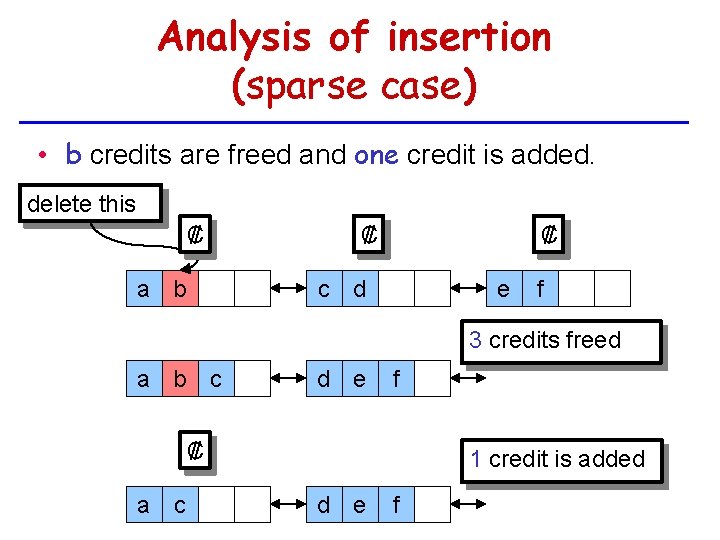
Analysis of insertion (sparse case) • b credits are freed and one credit is added. delete this ₡ a b ₡ ₡ c d e f 3 credits freed a b c d e f ₡ a c 1 credit is added d e f

Analysis wrap up • In a sequence of n add/remove operations – At most n/b takes O(b 2) time – Others take O(b) time • Total time is – O(nb + (n/b)b 2) = O(nb) – O(b) amortized time per operation

Compact doubly-linked list (summary) • Theorem: A Compact. DLList is an implementation of the List interface with the following properties: – get(i) and set(i, x) each take • O(1 + min{i, size()-i}/b) time – remove(i) and add(i, x) take • O(b + min{i, size()-i}/b) amortized time – The amount of memory used beyond that needed to store the data is O(n/b) – The number of memory allocation/deallocations during a sequence of n add/remove operations is O(n/b)