Priority Queues You will learn Implementations of priority

Priority Queues • You will learn – Implementations of priority queues – Practical uses of priority queues – We will cover the C++ code only for the basic priority queue implementation – We will cover selected alternative implementations on a conceptual basis only • Priority queues are important whenever, as the name implies, items have a priority value – Items are inserted into the priority queue – Items with the lowest (or highest) priority are removed

What is a priority queue • Basic operations – Insert new data; method of storage is dependent on the internal structure – Remove an item: for the queues we study the minimum will always be removed, but it is an easy change to make it the maximum that is always removed

Implementations based on Lists • Sorted list, assume size is N – Insertion is an O(N) operation – Deletion is a constant time operation • Unsorted list – Insertion is a constant time operation – Deletion is an O(N) operation • Performance over a longer period of time – Assume insertions and deletions are balanced – Both lists have O(N) performance overall – We need to do better

Binary Heap – Structure Property • The structure is a complete binary tree – Every level is filled, except possibly the lowest level – At the lowest level, the node are “to the left” as far as possible • For a tree of height h, there are between 2 h and 2 h+1 – 1 nodes • For a tree with n nodes, the height is log(n)

Array Implementation • Navigation properties – For an N node tree, the root is at index 1 and the last node in the tree is at index N – The left child, if present, is at index 2 i if the current index is i – The right child, if present, is at index 2 i+1 if the current index is i – The parent, if present, is at index i/2 (integer division) if the current index is i

Class Specification - 1 /* 1*/ /* 2*/ /* 3*/ // Note: the user must supply the routine Min_Val, // Which returns the minimum value of type Element_Type, // Which is used as a sentinel. /* 4*/ static const Default_Max_Size = 10; /* 5*/ /* 6*/ /* 7*/ /* 8*/ /* 9*/ /*10*/ /*11*/ template <class Element_Type> class Binary_Heap { private: unsigned int Max_Size; // Maximum number of elements. unsigned int Size; // Current number of elements. Element_Type *Elements; // The array. /*12*/ /*13*/ /*14*/ /*15*/ Binary_Heap( Binary_Heap & Value ); // Disabled. public: // Constructor. Binary_Heap( unsigned int Initial_Size = Default_Max_Size ); /*16*/ /*17*/ // Destructor. ~Binary_Heap( ) { delete [ ] Elements; } /*18*/ /*19*/ // Operator. const Binary_Heap & operator = ( const Binary_Heap & Value );

Class Specification - 2 /*20*/ /*21*/ /*22*/ /*23*/ /*24*/ /*25*/ /*26*/ /*27*/ // Member functions. void Make_Empty( ) { Size = 0; } int Is_Empty( ) const { return Size == 0; } int Is_Full( ) const { return Size == Max_Size; } void Insert( const Element_Type & X ); Element_Type Delete_Min( ); const Element_Type & Find_Min( ) const; }; /* 1*/ /* 2*/ /* 3*/ /* 4*/ /* 5*/ /* 6*/ /* 7*/ /* 8*/ /* 9*/ /*10*/ /*11*/ template <class Element_Type> Binary_Heap<Element_Type>: : Binary_Heap( unsigned int Initial_Size ) { Size = 0; Max_Size = Initial_Size; Elements = new Element_Type [ Max_Size + 1 ]; if( Elements == NULL ) Error( "Out of space!!" ); The minimum possible value Elements[ 0 ]= Min_Val( ); is stored at the “unused” array } position at index zero

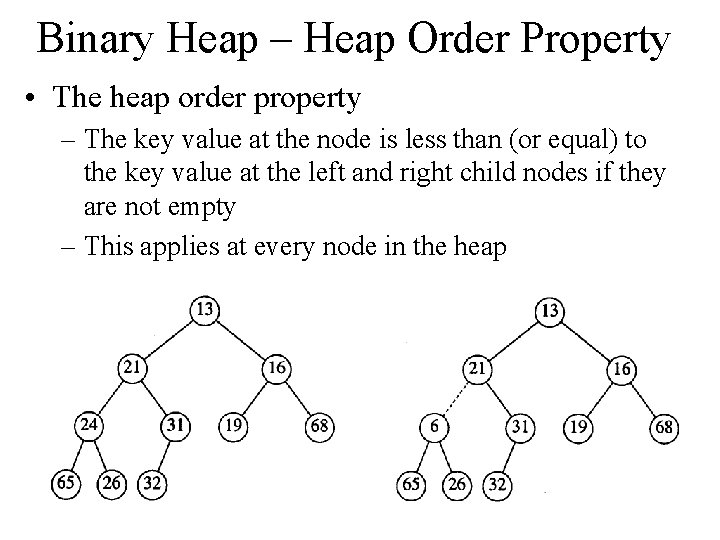
Binary Heap – Heap Order Property • The heap order property – The key value at the node is less than (or equal) to the key value at the left and right child nodes if they are not empty – This applies at every node in the heap

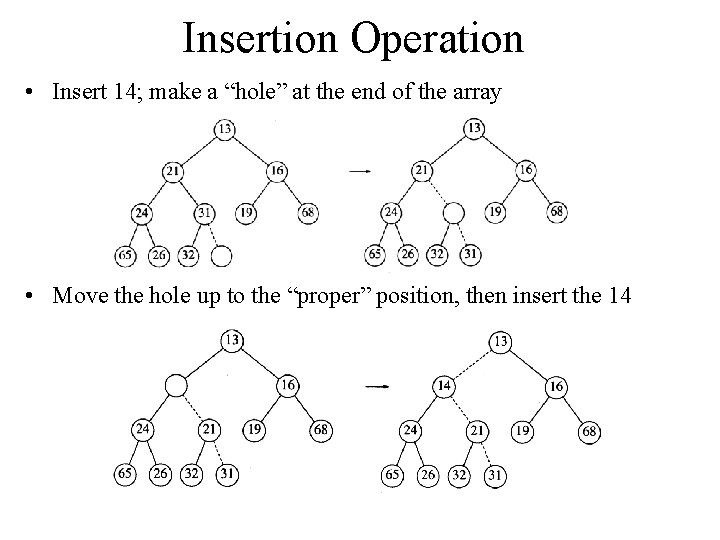
Insertion Operation • Insert 14; make a “hole” at the end of the array • Move the hole up to the “proper” position, then insert the 14

Insertion Code /* /* /* 1*/ 2*/ 3*/ 4*/ 5*/ 6*/ /* 7*/ /* 8*/ /* 9*/ /*10*/ /*11*/ /*12*/ /*13*/ /*14*/ /*15*/ /*16*/ /*17*/ /*18*/ /*19*/ template <class Element_Type> void Binary_Heap<Element_Type>: : Insert( const Element_Type & X ) { unsigned int i; if( Is_Full( ) ) Error( "Priority queue is full" ); else Start at the bottom { i = ++Size; While the heap order while( Elements[ i / 2 ] > X ) property is not satisfied { Elements[ i ] = Elements[ i / 2 ]; Move the current i /= 2; element down the heap } Elements[ i ] = X; } } Insert the new item at the correct position Move current index to the parent

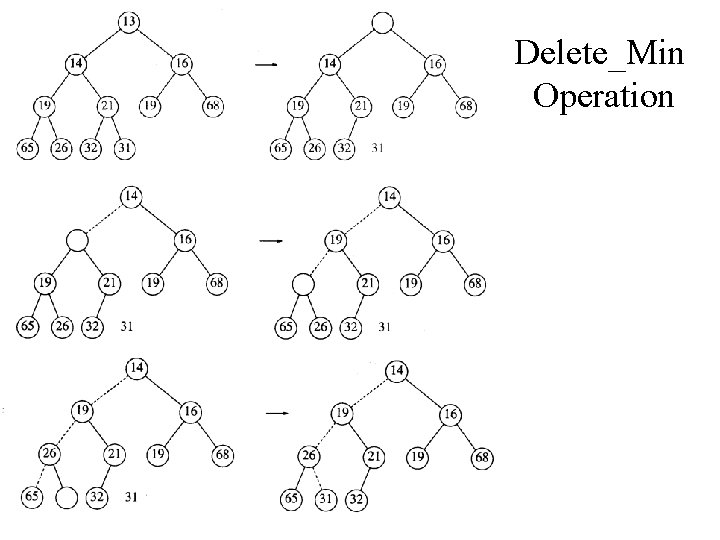
Delete_Min Operation

Delete_Min Code - 1 /* /* 1*/ 2*/ 3*/ 4*/ 5*/ 6*/ 7*/ template <class Element_Type> Element_Type Binary_Heap<Element_Type>: : Delete_Min( ) { unsigned int Child; Element_Type Min_Element, Last_Element; /* 8*/ /* 9*/ /*10*/ /*11*/ /*12*/ if( Is_Empty( ) ) { Error( "Priority queue is empty" ); return Elements[ 0 ]; // If error is not fatal. } /*13*/ /*14*/ Min_Element = Elements[ 1 ]; Last_Element = Elements[ Size-- ]; Retrieve the minimum element and decrease size of heap by one

Delete_Min Code - 2 /*15*/ /*16*/ /*17*/ /*18*/ /*19*/ /*20*/ /*21*/ /*22*/ /*23*/ /*24*/ /*25*/ /*26*/ /*27*/ /*28*/ /*29*/ /*30*/ } for( int i = 1; i * 2 <= Size; i = Child ) { Smaller child is at position // Find smaller child. 2 i or at position 2 i + 1 Child = i * 2; if( Child != Size ) if( Elements[ Child + 1 ] < Elements[ Child ] ) Child++; Move child up to parent position // Percolate one level. if( Last_Element > Elements[ Child ] ) Elements[ i ] = Elements[ Child ]; else break; Position is found, get } Elements[ i ] = Last_Element; return Min_Element; out of the loop now

Other Heap Operations • The following operations are useful for implementing priority queues as part of an operating system

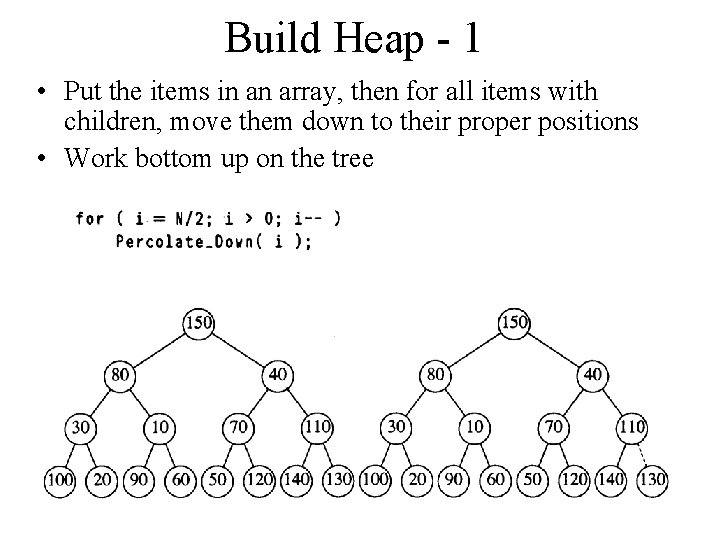
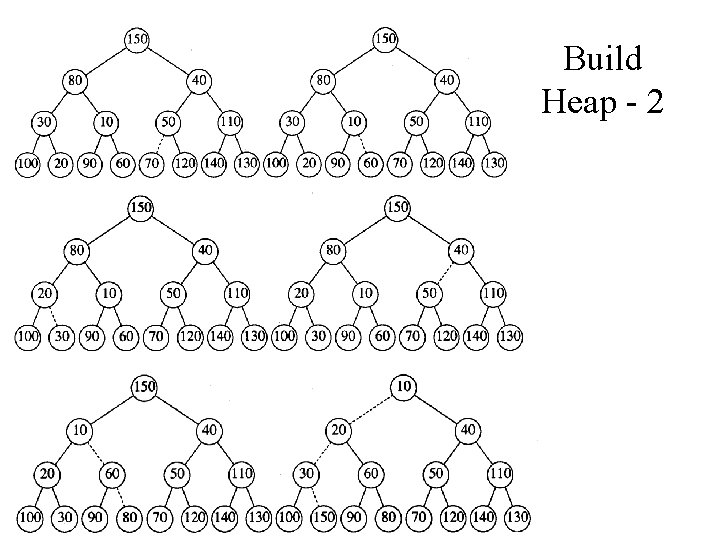
Build Heap - 1 • Put the items in an array, then for all items with children, move them down to their proper positions • Work bottom up on the tree

Build Heap - 2

Performance of Build Heap - 1 • A perfect tree is filled at the bottom level Proof • This result will establish an upper bound on the sum of heights for a complete binary tree

Performance of Build Heap - 2 • Example, suppose h = 4 and there are 31 nodes – one node is at height 4, 2 nodes at height 3, 4 nodes at height 2 and 8 nodes at height 1 – The sum of all the heights by brute force is 1*4 + 2*3 + 4*2 + 8*1 = 26 – By the formula the result is 2 h+1 – (h+1) = 25 – 1 – 5 = 26 • The significance of this analysis is that build heap can be performed in linear time