Quantum computation For computer scientists Prof Dorit Aharonov

Quantum computation For computer scientists Prof. Dorit Aharonov School of computer science and engineering Hebrew university, Jerusalem, Israel 1

What is a computation La Segrada Familia (Barcelona) Architect: Gaudi

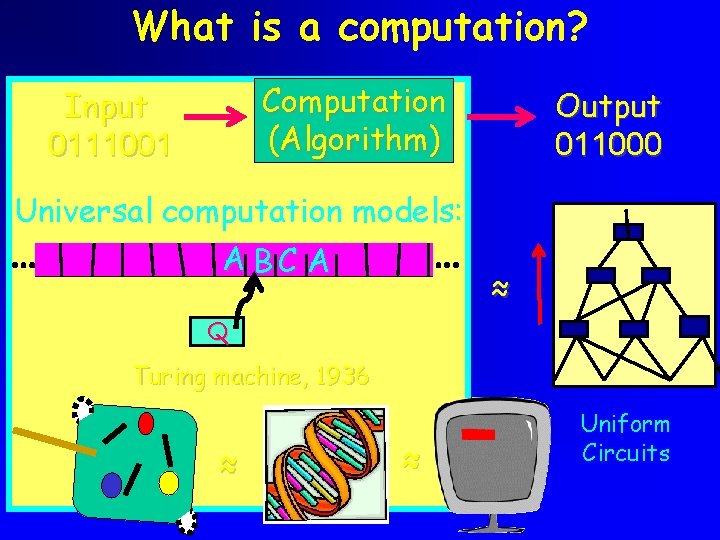
What is a computation? Computation (Algorithm) Input 0111001 Output 011000 Universal computation models: A BC A ≈ Q Turing machine, 1936 ≈ ≈ Uniform Circuits

Game of life Rules: A living site: stays alive if it has 2 or 3 live neighbors Otherwise dies A dead site: comes to life if it has exctly 3 living neighbors

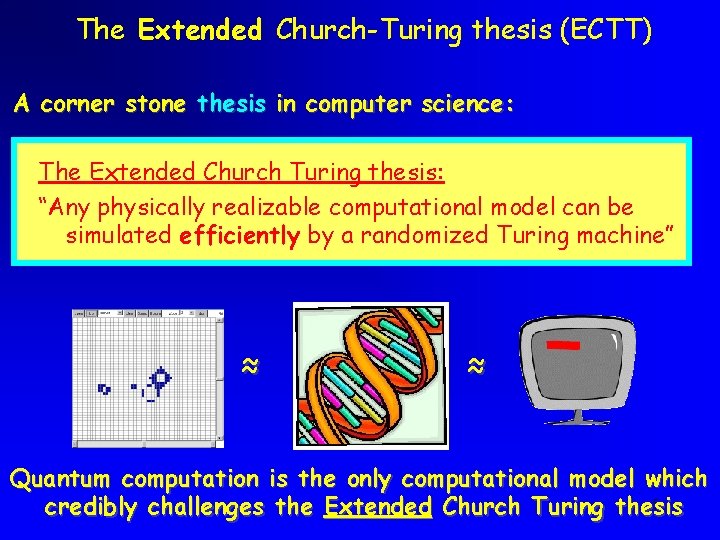
The Extended Church-Turing thesis (ECTT) A corner stone thesis in computer science: The Extended Church Turing thesis: “Any physically realizable computational model can be simulated efficiently by a randomized Turing machine” ≈ ≈ Quantum computation is the only computational model which 5 credibly challenges the Extended Church Turing thesis

Bird’s view on Quantum computation Inherently different from standard “classical” computers. We believe that it will be exponentially more powerful for certain tasks. Deutsch Josza [‘ 92] Bernstein Vazirani[‘ 93] Simon [‘ 94] Polynomial time Quantum algorithm for factoring Shor[’ 94] 6 Algorithms Physics of many particles (non universal computations) Cryptography technology Philosophy of Science

About this school Goal: Intro to quantum computation & complexity Some important notions, results, open questions Note: We will not cover many important things… (A partial list will be provided & updated ) Two remarks: 1) The lectures are intertwined, not independent! 2) The TA sessions are mainly exercises. Do them! We rely on them in the next lecture. 7

Intro Lecture: Qubits Part 1: The principles of quantum Physics Part 2: The qubit Part 3: Measurements Part 4: Dynamics Part 5: Two qubits 8

Part I: The principles of Quantum Physics 9

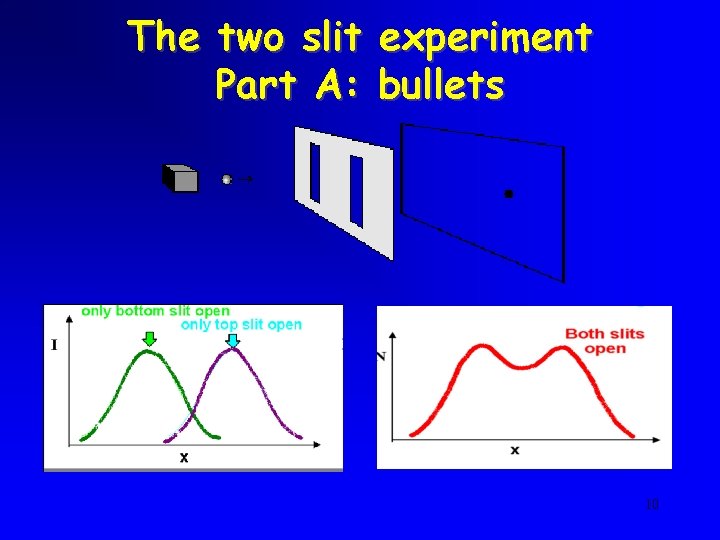
The two slit experiment Part A: bullets 10

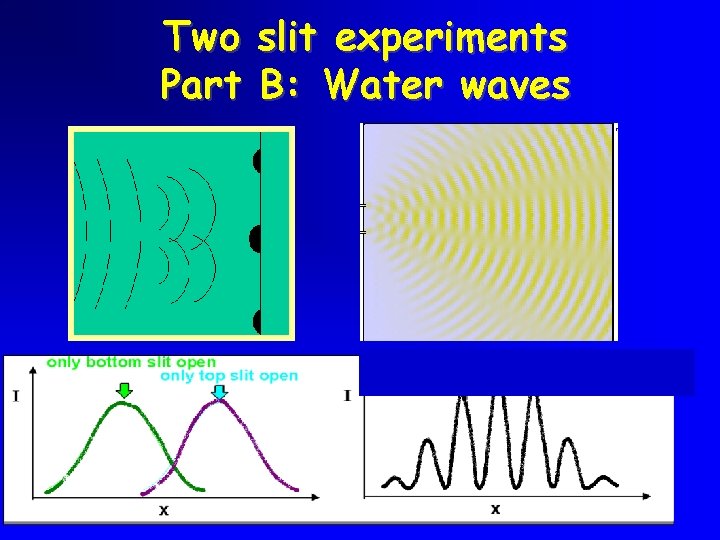
Two slit experiments Part B: Water waves 11

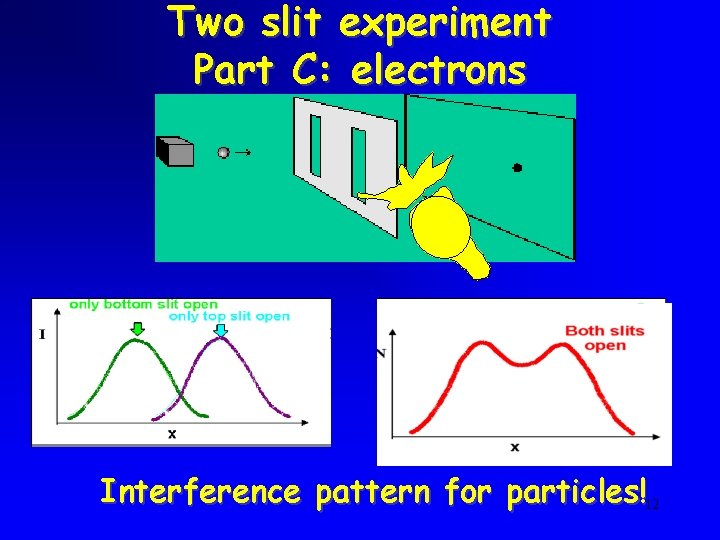
Two slit experiment Part C: electrons Interference pattern for particles!12

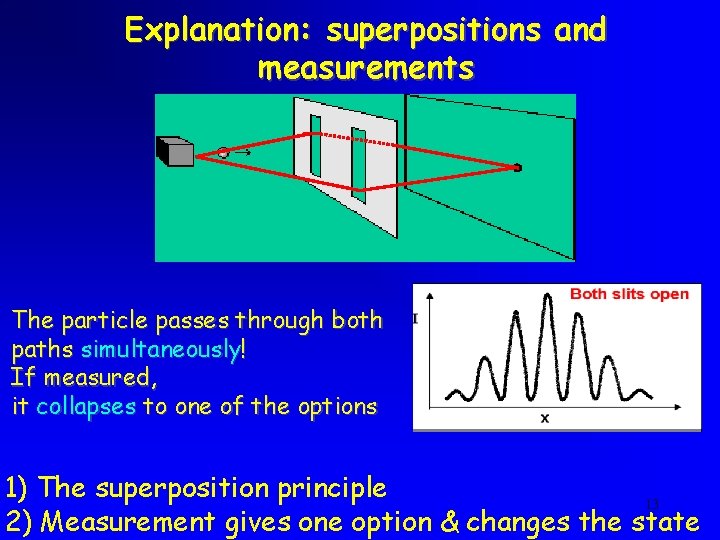
Explanation: superpositions and measurements The particle passes through both paths simultaneously! If measured, it collapses to one of the options 1) The superposition principle 13 2) Measurement gives one option & changes the state

Part II: The Qubit 14

st 1 quantum principle: Superposition a +b A quantum particle can be in a Superposition of all its possible “classical” states

The elementary quantum information unit: Qubit = Quantum bit The qubit can be in either one of the States: 0, 1 As well as in any linear combination! a vector in a 2 dim Hilbert space |0 We can also talk about qudits, Of higher dim. a 0 +b |1 1 On the board: Dirac notation Vector notation Transpose Inner products density matrix

Part III: Measurements 17

The quantum measurement a 0 0 +b 1 |a|2 |b|2 1 When a quantum particle is measured the answer is Probabilistic The Superposition collapses to one of its possible classical states nd 2 principle measurement Those (weird!) aspects have been tested in thousands of experiments 18

Projective measurements A projective measurement is described by a Hermitian matrix M. M has eigenvectors (eigenspaces) with associated real eigenvalues The classical outcome is eigenvalue �� with probability = norm squared of projection on the corresponsing eigenspace & the state collapses to this projection and renormlized 0 a 0 +b 1 1 On the board: Measure with respect to Z Prob=inner product squared Measure X: The +/- basis Probablity for �� a projection Expected value of measurement: Direct expression and as Tr(Mρ) Uncertainty principle

Part IV: Dynamics 20

Dynamics Schrodinger’s equation: The Hamiltonian (A Hermitian operator) Discrete time evolution: On the board: From the differential equation to unitary evolution (eigenvalues which are primitive roots of unity) Unitary as preserving inner product 21

Quantum Gates On the board: Applying X, Z on computational basis states of a qubit Linearity Applying Hadamard on basis states and measuring (“coin flip”) 22

Interference & path integrals |0 H |0 |0 |1 |1 H On the board: compute weights, repeat with measurement in the middle

Part V: Two qubits 24

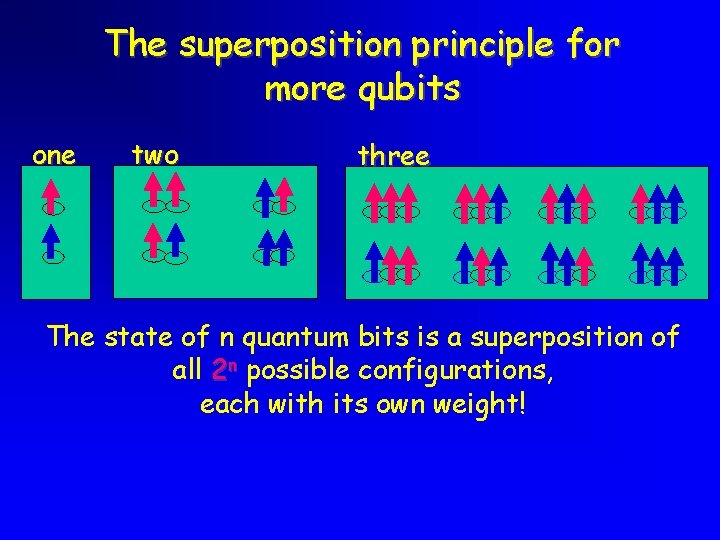
The superposition principle for more qubits one two three The state of n quantum bits is a superposition of all 2 n possible configurations, each with its own weight!

The space of two qubits The computational Basis for the two qubits space The EPR state:

1 st ex. of entanglement: The CHSH game They win if: !0. 85 < Pr(success) with EPR 27