Quality and Error Control Coding for DNA Microarrays










- Slides: 19

Quality and Error Control Coding for DNA Microarrays Olgica Milenkovic ECE Department University of Colorado, Boulder IEEE Denver Com. Soc

Outline • DNA Microarrays • VLSIPS (Very Large Scale Immobilized Polymer Synthesis) • Production of DNA Microarrays (http: //www. affymetrix. com/) – Base Scheduling – Mask Design – Quality-Control Coding • Error-Correcting DNA Microarrays (Multiplexed Arrays) • Production of Multiplexed DNA Microarrays – Base/Color Scheduling – Mask Design – Quality-Control Coding IEEE Denver Com. Soc

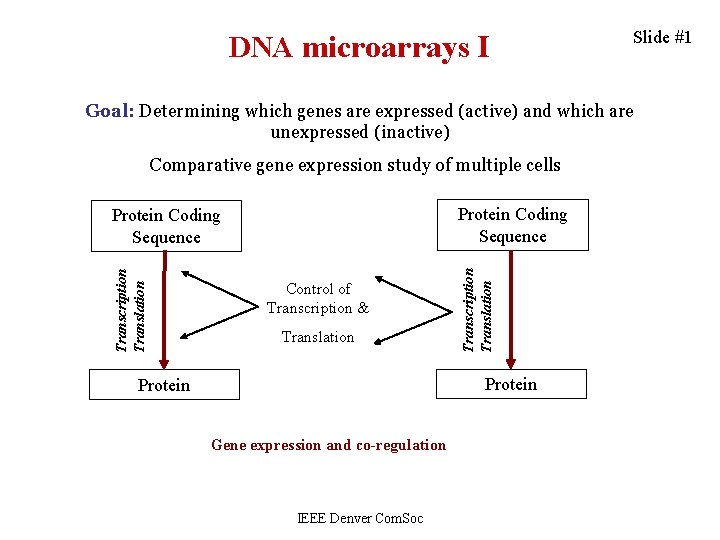
DNA microarrays I Slide #1 Goal: Determining which genes are expressed (active) and which are unexpressed (inactive) Comparative gene expression study of multiple cells Transcription Translation Control of Transcription & Translation Transcription Translation Protein Coding Sequence Protein Gene expression and co-regulation IEEE Denver Com. Soc

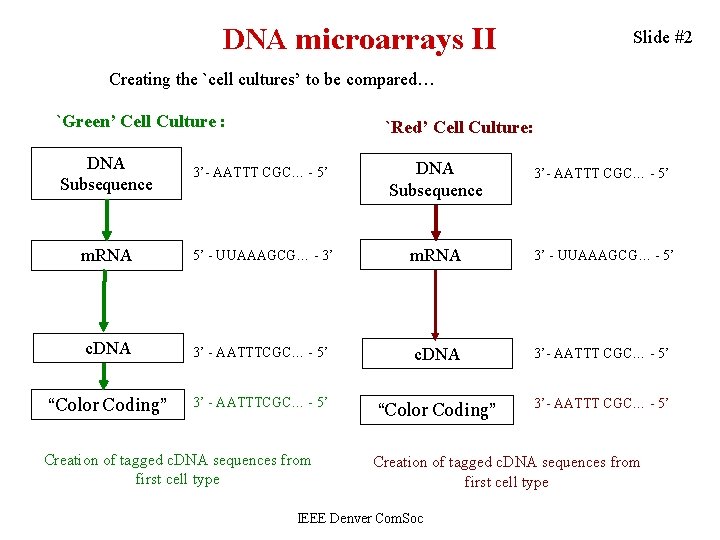
DNA microarrays II Slide #2 Creating the `cell cultures’ to be compared… `Green’ Cell Culture : `Red’ Cell Culture: DNA Subsequence 3’- AATTT CGC… - 5’ m. RNA 5’ - UUAAAGCG… - 3’ m. RNA 3’ - UUAAAGCG… - 5’ c. DNA 3’ - AATTTCGC… - 5’ c. DNA 3’- AATTT CGC… - 5’ “Color Coding” 3’ - AATTTCGC… - 5’ “Color Coding” 3’- AATTT CGC… - 5’ Creation of tagged c. DNA sequences from first cell type IEEE Denver Com. Soc

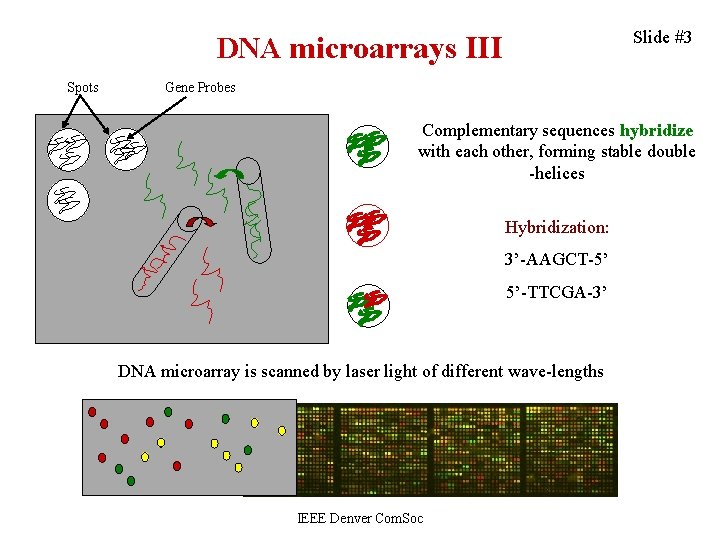
Slide #3 DNA microarrays III Spots Gene Probes Complementary sequences hybridize with each other, forming stable double -helices Hybridization: 3’-AAGCT-5’ 5’-TTCGA-3’ DNA microarray is scanned by laser light of different wave-lengths IEEE Denver Com. Soc

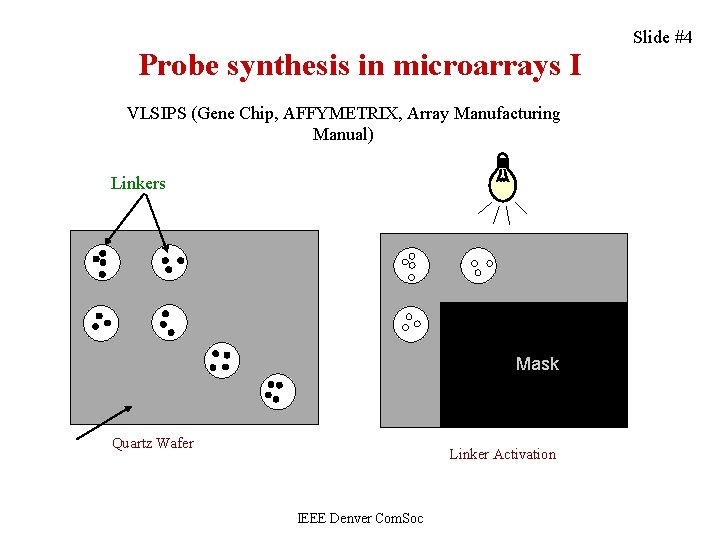
Probe synthesis in microarrays I VLSIPS (Gene Chip, AFFYMETRIX, Array Manufacturing Manual) Linkers Mask Quartz Wafer Linker Activation IEEE Denver Com. Soc Slide #4

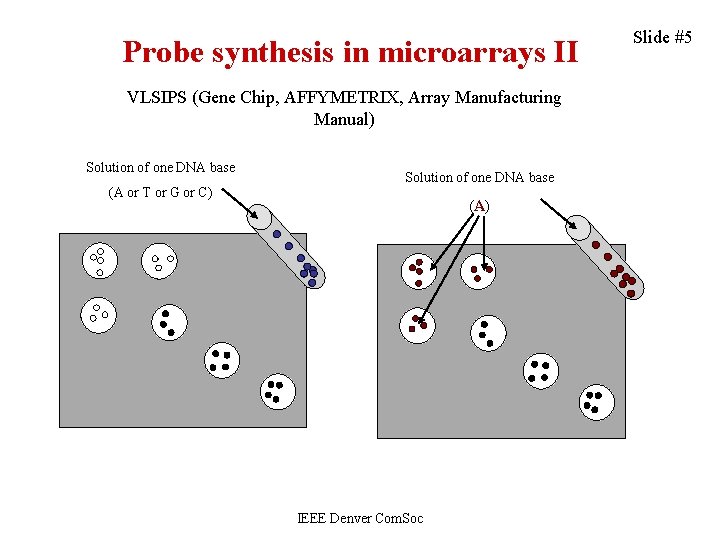
Probe synthesis in microarrays II VLSIPS (Gene Chip, AFFYMETRIX, Array Manufacturing Manual) Solution of one DNA base (A or T or G or C) Solution of one DNA base (A) IEEE Denver Com. Soc Slide #5

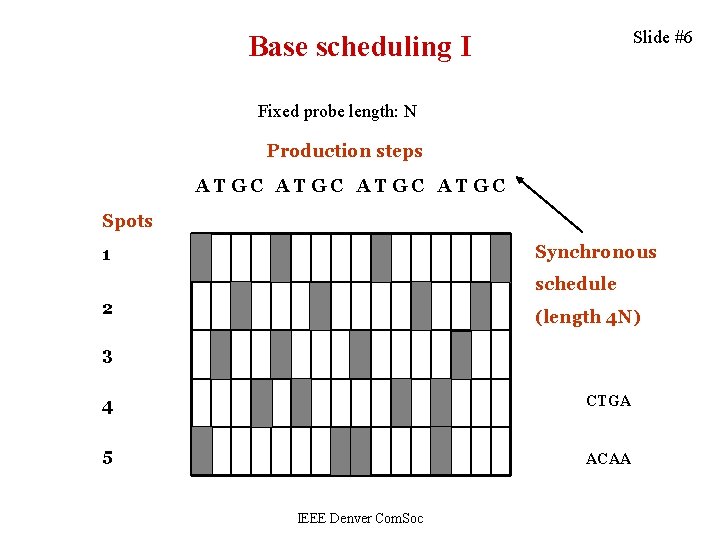
Slide #6 Base scheduling I Fixed probe length: N Production steps ATGC Spots Synchronous 1 schedule 2 (length 4 N) 3 4 CTGA 5 ACAA IEEE Denver Com. Soc

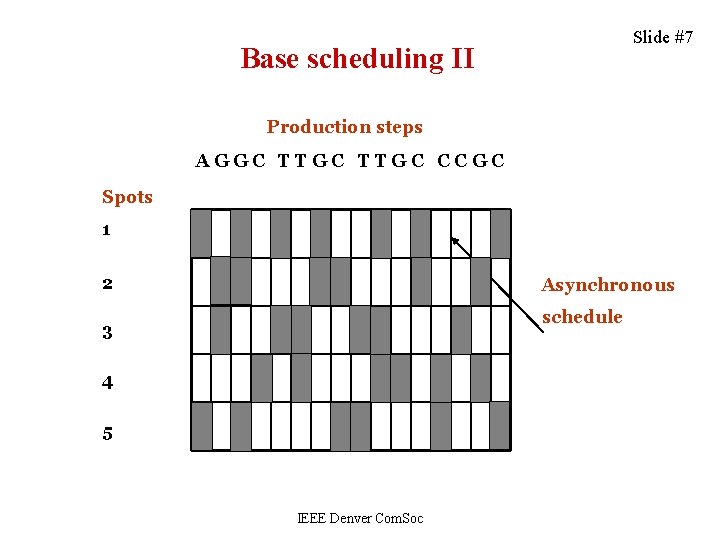
Slide #7 Base scheduling II Production steps AGGC TTGC CCGC Spots 1 2 Asynchronous schedule 3 4 5 IEEE Denver Com. Soc

Base Scheduling III • Slide #8 Shortest asynchronous base schedule – Shortest common super-sequence of set of M sequences (NP-hard) ESN(M, k) – expected length of a longest common subsequence of M randomly chosen sequences of length N over an alphabet of size k No significant gain for N≈20 -30 Periodic schedule used instead (length 4 N) IEEE Denver Com. Soc

Mask Design Slide #9 Border-length minimization Feldman and Pevzner, 1994 Hannehalli et. al. , 2002 Kahng et. al. 2003, 2004 Key idea: Arrange the probes on the array in such a way that the border-length of all masks is minimal Border-length graph: complete graph on M vertices, weight of edges equal to the Hamming distance between probes Greedy traveling salesman algorithm+ threading (discrete space-filing curve) IEEE Denver Com. Soc

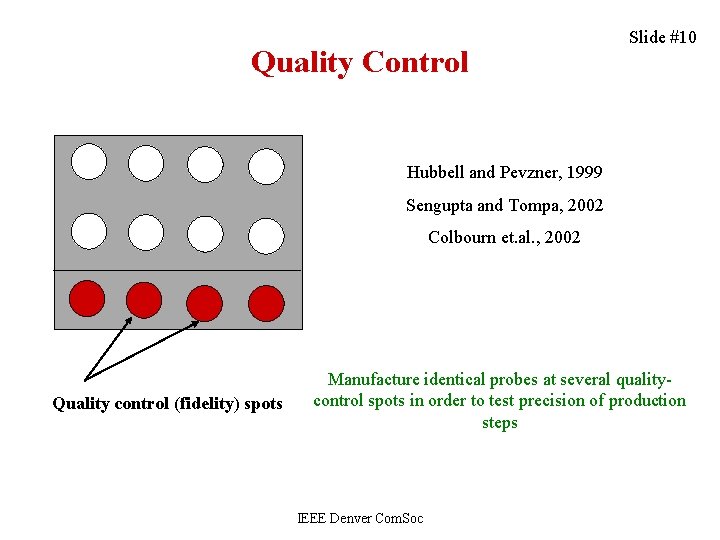
Quality Control Slide #10 Hubbell and Pevzner, 1999 Sengupta and Tompa, 2002 Colbourn et. al. , 2002 Quality control (fidelity) spots Manufacture identical probes at several qualitycontrol spots in order to test precision of production steps IEEE Denver Com. Soc

Relevant coding-theoretic ideas Slide #11 Balanced code (Sengupta and Tompa, 2002): An b×v binary matrix of zeros and ones with • each row has weight k; • each column has weight bounded between l and b-l, for some constant l; • any pair of columns is at least at Hamming distance d apart; Superimposed designs in Renyi’s search model (Kautz and Singleton, 1964, Dyachkov and Rykov, 1983): An b×v binary matrix of zeros and ones with • all Boolean sums composed of no more than s columns are distinct; • each row has weight exactly t; Additional constraints: the Boolean sums form an error-correcting code with prescribed minimum distance d; IEEE Denver Com. Soc

Slide #12 Error-correcting microarray design • Probe multiplexing (Khan et. al, 2003) Probes Excluding hybridization effects, spot formation quality and under iid measurement noise, s p o t s X – vector of RNA levels corresponding to N genes Y – total concentration of RNA at all spots S - hybridization affinity matrix, T - spot quality matrix Decoding algorithm: numerical optimization IEEE Denver Com. Soc

VLSIPS/analysis for multiplexed arrays Slide #13 Features: • Multiple polymer synthesis at one given spot (for simplicity, will consider only two probes per spot) • Can use two different classes of linkers sensitive to different wavelengths so to select probes for extension (say, `blue’ and `green’ and `cyan’) Spot s A T G C g b c c A T G C g g c b g 1 2 3 4 5 6 g b b c b

Slide #14 VLSIPS/analysis for multiplexed arrays Scheduling: shortest schedule of bases/colors (Using results from V. Dancık, Expected Length of Longest Common Subsequences, 1994) Set-up: two identical sets of M `blue’ and M `green’ randomly and uniformly chosen sequences of length N over the alphabet of size four Length of shortest schedule Chvatal-Sankoff constants Synchronous schedule, no `cyan’ colored steps: 8 N IEEE Denver Com. Soc

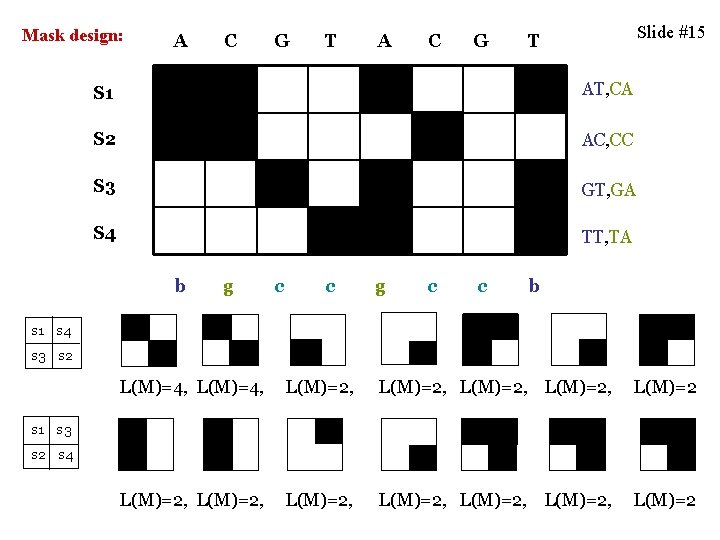
Mask design: A C G T A C G Slide #15 T S 1 AT, CA S 2 AC, CC S 3 GT, GA S 4 TT, TA b g c c b s 1 s 4 s 3 s 2 L(M)=4, L(M)=2, L(M)=2, L(M)=2, L(M)=2 s 1 s 3 s 2 s 4

Mask Design / Scheduling Slide #16 Neighborhood graph: complete graph with M vertices labeled by two distinct sequences No `cyan’ steps: weight of edge between two vertices sums of Hamming distances Issues: For reasons of controlled hybridization, different probes (blue and green) at the same spot should have fairly large Hamming distance (Milenkovic and Kashyap, 2005) Border-length minimization becomes less effective With cyan colored steps involved, the distance measure also depends on the longest common subsequence of the probes at the same spot IEEE Denver Com. Soc

Quality Control Coding Slide #17 Theorem: Assume that there exists a linear error-control code with parameters [n, k, d] containing the all-ones codeword. Then one can construct a quality control array for a multiplexed DNA chip with 2(2 k-2) disjoint blue and green production steps and M probes such that the length of each quality control probe is 2(k-1)-1, and that the weights w of the columns in the quality control array satisfy Furthermore, with such an array any collection of less than n/(n-d) failed blue or green steps, respectively, can be uniquely identified. Open question: how does one extend this result for schedules involving `cyan’ colored production steps, and under `spot’ failures. IEEE Denver Com. Soc
 Coding dna and non coding dna
Coding dna and non coding dna Selective coding
Selective coding Open coding
Open coding Quality assurance vs quality control
Quality assurance vs quality control Quality control concepts
Quality control concepts Flow and error control
Flow and error control History of qualitative research
History of qualitative research Project quality management pmp
Project quality management pmp Quality metrics pmp
Quality metrics pmp Hdlc adalah
Hdlc adalah Type 1 type 2 error power
Type 1 type 2 error power Absolute or relative error
Absolute or relative error Round off error and truncation error
Round off error and truncation error Difference between error detection and error correction
Difference between error detection and error correction How do you do percent error
How do you do percent error Quality teaching rounds coding sheet
Quality teaching rounds coding sheet Dna polymerase function in dna replication
Dna polymerase function in dna replication Bioflix activity dna replication lagging strand synthesis
Bioflix activity dna replication lagging strand synthesis The principal enzyme involved in dna replication is
The principal enzyme involved in dna replication is Dna and genes chapter 11
Dna and genes chapter 11





































