PROPORCIONALIDAD Y PORCENTAJES Debers hacer clic con el

PROPORCIONALIDAD Y PORCENTAJES Deberás hacer clic con el botón izquierdo del ratón para avanzar paso a paso

PROPORCIONALIDAD 1. - Proporcionalidad directa A doble en la primera magnitud, doble en la segunda Naranjas (kg) 2 3 4 5 Precio (€) 4 6 8 10 2 (es lo que corresponde a 1) En una tabla de proporcionalidad directa, el cociente de cada pareja de valores correspondientes es constante. Ello nos sirve para comprobar si una tabla es de proporcionalida directa y para completar tablas incompletas A 2 3 4 5 B 12 18 24 30 A 4 B 20 5 10 50 Es una tabla de proporcionalidad directa (los cocientes son iguales) A 4 2 5 10 B 20 10 25 50

PROPORCIONALIDAD 2. - Proporcionalidad inversa A doble en la primera magnitud, mitad en la segunda Operarios 2 3 4 8 Tiempo (h) 12 8 6 3 2. 12 = 3. 8 = 4. 6 = 8. 3 = 24 (es lo que corresponde a 1) En una tabla de proporcionalidad inversa, el producto de cada pareja de valores correspondientes es constante. Ello nos sirve para comprobar si una tabla es de proporcionalidad inversa y para completar tablas incompletas. A 2 3 4 10 B 12 8 6 2, 4 A 4 B 9 6 12 18 Es una tabla de proporcionalidad inversa (los productos son iguales) A 4 3 6 2 B 9 12 6 18

PROPORCIONALIDAD 3. - Fracciones equivalentes en las tablas de proporcionalidad Propocionalidad directa Propocionalidad inversa Naranjas (kg) Precio (€) Operarios Tiempo (h) 2 4 2 12 3 6 3 8 4 6 5 10 6 4 En las tablas de proporcionalidad directa, la fracción formada con un par de valores de la primera magnitud es equivalente a la fracción formada con los valores correspondientes en la otra magnitud. En las tablas de proporcionalidad inversa, la fracción formada con un par de valores de la primera magnitud es equivalente a la inversa de la fracción formada con los valores correspondientes en la otra magnitud.

PROPORCIONALIDAD 4. - Problemas de proporcionalidad directa En una fábrica, 8 máquinas producen 120 piezas. ¿Cuántas piezas producirán 25 máquinas? POR REDUCCIÓN A LA UNIDAD Máquinas Pieza 8 25 120 ? 120 : 8 = 15 25. 15 = 375 POR REGLA DE TRES Máquinas Piezas 8 ---- 120 25 ---- x D D = 375 Solución: 375 piezas

PROPORCIONALIDAD 5. - Problemas de proporcionalidad inversa Doce operarios hacen un trabajo en 6 días. ¿ En cuánto lo harán 8 operarios ? ¿ Y 3 operarios ? POR REDUCCIÓN A LA UNIDAD Oper 12 8 3 Días 6 ? ? I 12. 6 = 72 72 : 8 = 9 72 : 3 = 24 Solución: 9 días 24 días POR REGLA DE TRES Operarios Días 12 ---- 6 8 ---- x 3 ---- y I Solución: 9 días 24 días

PROPORCIONALIDAD 6. -¿Cómo resolver problemas por regla de tres? Para resolver un problema de proporcionalidad debes seguir los siguientes pasos: 1º. - Determinar si la proporcionalidad entre las magnitudes es directa o inversa 2º. - Plantear la regla de tres señalando si es directa o inversa. Expresa las cantidades de cada magnitud en la misma unidad. 3º. - Escribir la pareja de fracciones equivalentes. 4º. - Hallar x Fíjate en los siguientes ejemplos. Para realizar cierto trabajo 10 obreros emplean 8 horas. ¿Cuánto les hubiera costado a 16 obreros? (Es inversa porque a doble de obreros mitad de tiempo) Si por 12 camisetas pago 96 €, ¿cuánto pagaré por 57 de esas camisetas? ( Es directa porque a doble de camisetas doble dinero) Camisetas Dinero(€) 12 ------- 96 57 ---- x Nº obreros Tiempo (h) 10 ----- 8 16 ----- x D I Solución 5 horas Solución 456 €

PORCENTAJES 7. - Concepto de porcentaje La expresión porcentaje o tanto por ciento equivale a “tantos de cada 100”. Es decir, hablar del 40% es hablar de 40 de cada 100. Teniendo en cuenta lo anterior, para hallar un tanto por ciento de una cantidad deberíamos dividir primero por 100 para ver cuántas cientos hay en la cantidad y después multiplicaríamos por el tanto por ciento. Así, para hallar el 35% de 420 haríamos lo siguiente: 420 : 100 = 4, 2. 35 = 147 En la práctica lo haremos de otras formas pero esta idea nos puede venir bien para calcular mentalmente –o con cálculos sencillos- tantos por cientos en los que aparecen ceros al final de las cantidades. Recuerda que para dividir por 100 un número que acaba en ceros lo que hacemos es quitar dos ceros. Por ello, para calcular estos porcentajes quitaremos dos ceros y multiplicaremos las cantidades resultantes: 4% de 600 = 4. 6 = 24 20% de 60 = 2. 6 = 12 30% de 50 = 3. 5 = 15 8% de 2000 = 8. 20 = 160 40% de 500 = 40. 5 = 200 4% de 50 = 4. 0, 5 = 2 (*) En este último ejemplo lo mejor es multiplicar 4 por 5 (sólo hemos quitado un cero) y del resultado, 20, quitar el segundo cero y llegar al resultado final, 2.

PORCENTAJES 8. - Cálculo de porcentajes: porcentaje como fracción Hemos visto que 40% es lo mismo que 40 de cada 100. Pero resulta que 40 de cada 100 también lo podemos expresar en forma de fracción: 40/100. Es decir, 40% = Por ello, hallar el 40% de 600 será lo mismo que calcular procederemos así: 35 % de 60 = de 600. En la práctica 21 A esta forma de calcular porcentajes la llamaremos porcentaje como fracción o también “con lápiz y papel” 28% de 420 = 117, 6 150% de 36 = 54

PORCENTAJES 9. - Cálculo de porcentajes: porcentaje como regla de tres Podemos interpretar el cálculo de un porcentaje como un problema de proporcionalidad directa. Por ello, también podremos calcularlos por medio de una regla de tres. Ejemplo: Calcular 40% de 650 Total Parte 100 ------ 40 650 ------ x Esta forma de calcular los porcentajes es particularmente útil para resolver algunos problemas.

PORCENTAJES 10. - Cálculo de porcentajes: con calculadora Calcular 35% de 60 CALCULADORA NO CIENTÍFICA Deberás teclear: CALCULADORA CIENTÍFICA La secuencia de teclas depende del modelo de calculadora. Para la Casio es: 60 x 35 % 60 x 35 SHIFT = y aparecerá el resultado en la pantalla SHIFT 21 Tecla = activa la segunda función de las teclas contiene % como segunda función SHIFT + = % SHIFT = %

PORCENTAJES 11. - Cálculo rápido de algunos porcentajes: 10% = décima parte (: 10) 50% = la mitad (: 2) 10% de 42 = 42 : 10 = 4, 2 50% de 36 = 36 : 2 = 18 25% = la cuarta parte (: 4) 25% de 40 = 40 : 4 = 10 20% = la quinta parte (: 5) 20% de 35 = 35 : 5 = 7 75% = las tres cuartas partes (: 4) y (x 3) 75% de 16 = 16 : 4. 3 = 12

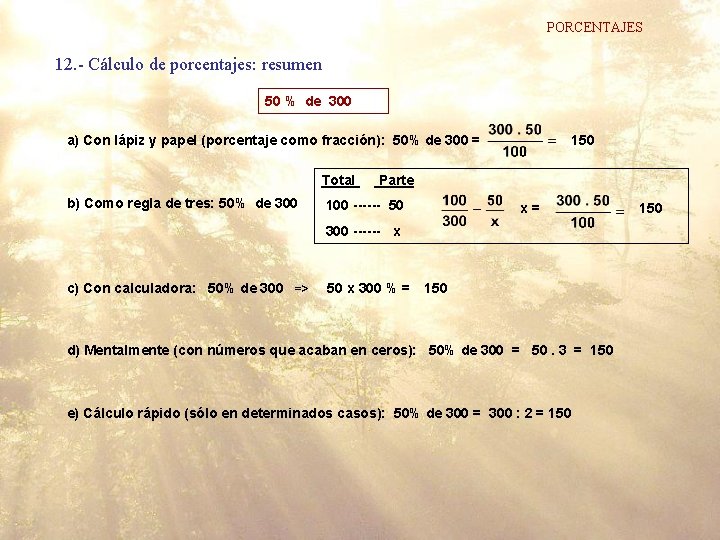
PORCENTAJES 12. - Cálculo de porcentajes: resumen 50 % de 300 a) Con lápiz y papel (porcentaje como fracción): 50% de 300 = Total b) Como regla de tres: 50% de 300 150 Parte 100 ------ 50 x= 300 ------ x c) Con calculadora: 50% de 300 => 50 x 300 % = 150 d) Mentalmente (con números que acaban en ceros): 50% de 300 = 50. 3 = 150 e) Cálculo rápido (sólo en determinados casos): 50% de 300 = 300 : 2 = 150

PORCENTAJES 13. -Problemas de porcentajes 1 Asignaremos nombres a los diferentes elementos que integran el cálculo de un tanto por ciento: 30% de 40 = 12 porcentaje parte total A- CÁLCULO DE LA PARTE En mi clase, el 40% son chicas. Si en total somos 30, ¿cuántas son las chicas? (El problema se resuelve hallando el 40% de 30 por cualquiera de los métodos que conocemos) total : 30 chicas: 40% de 30 = 12 Solución: 12 chicas

PORCENTAJES 14. - Problemas de porcentajes 2 B- CÁLCULO DEL PORCENTAJE En mi clase, de 30 que somos en total, 12 son chicas. ¿Qué porcentaje representan las chicas? (Lo resolveremos por regla de tres. Y recuerda que el porcentaje es lo que corresponde a 100) Total Chicas Solución: 30 --- 12 40% 100 --- x Otra forma de resolverlo Alumnos % 30 ------- 100 12 ------- x Solución: 40%

PORCENTAJES 15. - Problemas de porcentajes 3 C- CÁLCULO DEL TOTAL En mi clase hay 12 chicas y representan el 40% del total. ¿Cuántos somos en total? (Lo resolveremos por regla de tres. Y recuerda que el porcentaje es lo que corresponde a 100) Total Chicas Solución: 100 --- 40 x 30 alumnos/as --- 12 Otra forma de resolverlo % Alumnos/as 40 ----- 12 100 ----- x Solución: 30 alumnos/as

PORCENTAJES 16. - Problemas de porcentajes 4 D- AUMENTO PORCENTUAL Son problemas en los que algo tiene un valor inicial, aumenta en un porcentaje de su valor y llega a un valor final. Mi tío gana 1200 € mensuales de sueldo y le van a subir el 12%. ¿Cuánto ganará después de la subida? Sueldo: 1200 € 12% de 1200 = 144 Aumento: 12% 1200 + 144 = 1344 Otra forma de resolverlo Sueldo: 1200 € Aumento: 12% Solución: 1344 € (Si aumenta el 12%, cada 100 de antes se convienten en 112) 112% de 1200 = 1344 Solución: 1344 €

PORCENTAJES 17. - Problemas de porcentajes 5 E- DISMINUCIÓN PORCENTUAL Son problemas en los que algo tiene un valor inicial, disminuye en un porcentaje de su valor y llega a un valor final. La camiseta que me gusta vale hoy 30 €. Si en rebajas tiene un descuento del 25%. ¿Cuánto me costará entonces? Precio: 30€ Decuento: 25% Otra forma de resolverlo Precio: 30€ Decuento: 25% de 30 = 7, 5 30 – 7, 5 = 22, 5 Solución: 22, 5 € (Si me descuentan el 25%, pago el 75% del valor) 75% de 30 = 22, 5 Solución: 22, 5 €

PORCENTAJES 18. - Otros problemas de aumento y disminución porcentual Son problemas en los que se nos pide averiguar el valor inicial conociendo el valor final y el porcentaje de aumento o disminución. Los resolveremos por regla de tres Mi tío gana 1344 € mensuales de sueldo después de una subida del 12%. ¿Cuánto ganaba antes? Antes Después 100 --- 112 x --- 1344 Solución: 1200 € He pagado 22, 50 € por una camiseta. Si me han descontado el 25%, ¿cuál era el precio antes de la rebaja? Antes Después 100 --- 75 x --- 22, 50 Solución: 30 30 €