Projektowanie cyfrowych systemw w oparciu o ukady VLSI

Projektowanie cyfrowych systemów w oparciu o układy VLSI i PLD Ernest Jamro, AGH Kraków Cordic, Dzielenie, Pierwiastek. . .

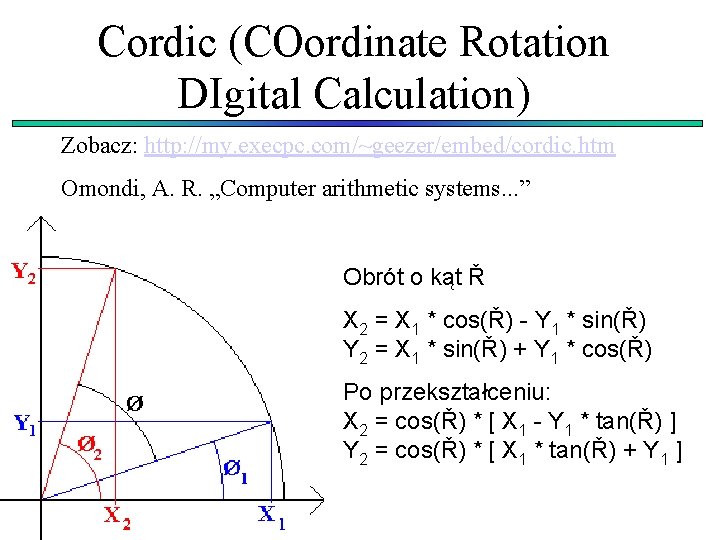
Cordic (COordinate Rotation DIgital Calculation) Zobacz: http: //my. execpc. com/~geezer/embed/cordic. htm Omondi, A. R. „Computer arithmetic systems. . . ” Obrót o kąt Ř X 2 = X 1 * cos(Ř) - Y 1 * sin(Ř) Y 2 = X 1 * sin(Ř) + Y 1 * cos(Ř) Po przekształceniu: X 2 = cos(Ř) * [ X 1 - Y 1 * tan(Ř) ] Y 2 = cos(Ř) * [ X 1 * tan(Ř) + Y 1 ]

CORDIC – c. d. Wybieramy tg(Ř) tak aby = 1, ½, ¼, . . . Wtedy: tan(Ř 21) = 1/1 Ř 21 = 45° tan(Ř 32) = 1/2 Ř 32 = 26. 5650° tan(Ř 43) = 1/4 Ř 43 = 14. 0362° tan(Ř 54) = 1/8 Ř 54 = 7. 12502° tan(Ř 65) = 1/16 Ř 65 = 3. 57633° tan(Ř 76) = 1/32 Ř 76 = 1. 78991° cos(Ř 21) = 0. 707107 cos(Ř 32) = 0. 894427 cos(Ř 43) = 0. 970142 cos(Ř 54) = 0. 992278 cos(Ř 65) = 0. 998053 cos(Ř 76) = 0. 999512 W rezultacie: Mnożenie przez tan(Ř)- zastępujemy przez dodawanie z przesunięciem Mnożenie przez cos(Ř) jest zastępowane przez pojedyncze mnożenie skumulowane przez stałą wartość (zob. następna strona) cos(Ř 21)* cos(Ř 32) * cos(Ř 43) *. . .

CORDIC – Iteracje Iteracja 1 X 2 = cos(Ř 21) * [ X 1 - Y 1 * tan(Ř 21) ] Y 2 = cos(Ř 21) * [ X 1 * tan(Ř 21) + Y 1 ] Iteracja 2 X 3 = cos(Ř 32) * { X 2 - Y 2 * tan(Ř 32) } Y 3 = cos(Ř 32) * { X 2 * tan(Ř 32) + Y 2 } itd. Mnożenie przez cos(Ř) można wykonać na samym końcu a nie w każdej iteracji.

CORDIC Przykład Znaleźć sin(28. 027°) Stan początkowy: Ř = 0° cos(Ř) = 1 X = 1 sin(Ř) = 0 Y = 0 Rotacja o 45° X' = X - Y / 1 = 1 - 0 / 1 = 1 Y' = X / 1 + Y = 1 / 1 + 0 = 1 Rotacja z 45° do 18. 435° (Ř 32 = -26. 565°) (Przesunięcie o kąt ujemny ale cos(-Ř)= cos(Ř) więc nie ma to wpływu na wartość skumulowanego iloczynu. Obracamy o kąt ujemny wtedy kiedy skumulowany kąt obrotu jest większy od kąta docelowego. ) X' = X + Y / 2 = 1 + 1 / 2 = 1. 5 Y' = -X / 2 + Y = -1 / 2 + 1 = 0. 5 Rotacja z 18. 435° do 32. 471° (Ř 43 = 14. 036°) X' = X - Y / 4 = 1. 5 - 0. 5 / 4 = 1. 375 Y' = X / 4 + Y = 1. 5 / 4 + 0. 5 = 0. 875

CORDIC Przykład - c. d. Rotacja z 32. 471° do 25. 346° (Ř 54 = -7. 125°) X' = X + Y / 8 = 1. 375 + 0. 875 / 8 = 1. 484375 Y' = -X / 8 + Y = -1. 375 / 8 + 0. 875 = 0. 703125. . . Rotacja 27. 132° do 28. 027° (Ř 87 = 0. 895°) X' = X - Y / 64 = 1. 465300 - 0. 750884 / 64 = 1. 453567 Y' = X / 64 + Y = 1. 465300 / 64 + 0. 750884 = 0. 773779 W rezultacie: sin(28. 027°) = 0. 607253 * Y = 0. 46988 cos(28. 027°) = 0. 607253 * X = 0. 88268 Zamiast mnożyć przez skumulowany czynnik cos(Ř) można ustawić: X= 0. 607253 zamiast 1 w pierwszej iteracji. Kąt Ř w każdej iteracji powinien być zapisany w pamięci LUT (w przypadku implementacji sekwencyjnej) w przypadku implementacji kaskadowej jest on wartością stałą.

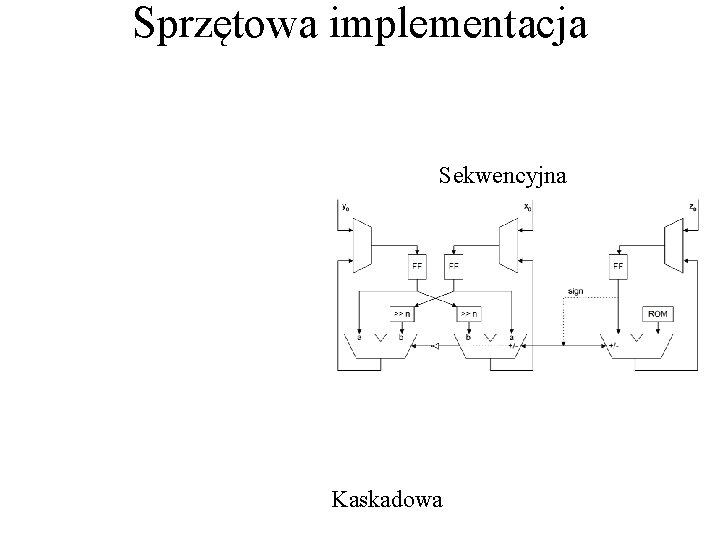
Sprzętowa implementacja Sekwencyjna Kaskadowa

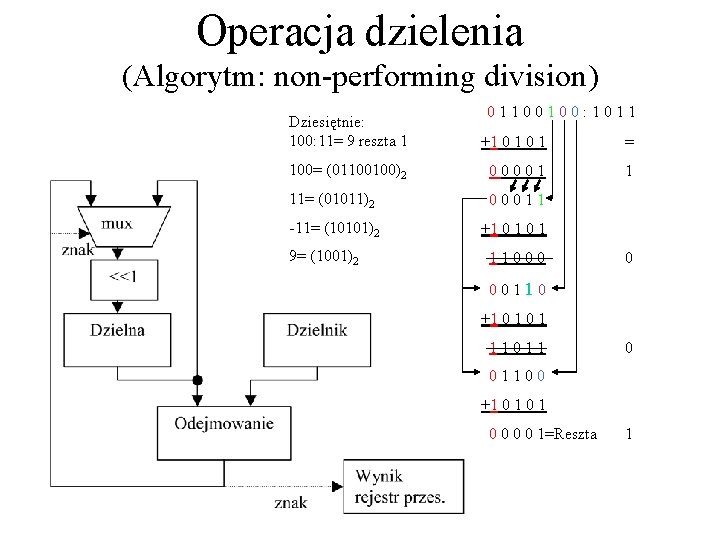
Operacja dzielenia (Algorytm: non-performing division) 01100100: 1011 Dziesiętnie: 100: 11= 9 reszta 1 +1 0 1 = 100= (01100100)2 00001 1 11= (01011)2 00011 -11= (10101)2 +1 0 1 9= (1001)2 11000 0 00110 +1 0 1 11011 0 01100 +1 0 1 0 0 1=Reszta 1

Pozycjonowanie (normalizacja) argumentów dzielenia Aby przyspieszyć operacje dzielenia należy najpierw odpowiednio przesunąć bitowo dzielną i dzielnik – tak aby na najbardziej znaczących bitach występowały ‘ 1’ Przykład: a) 1001: 0011 należy zastąpić przez 1001: 1100 a wynik podzielić przez 4 ( przesunąć w prawo o 2 bity) w ten sposób zyskujemy 2 takty zegara b) 01100: 000101 należy zastąpić przez 11000 ( <<1) oraz 101000 (<<3) czyli wynik należy podzielić przez 4 (>>2) Dokładniejszy opis normalizacja można znaleźć w wykładzie liczby zmiennoprzecinkowe

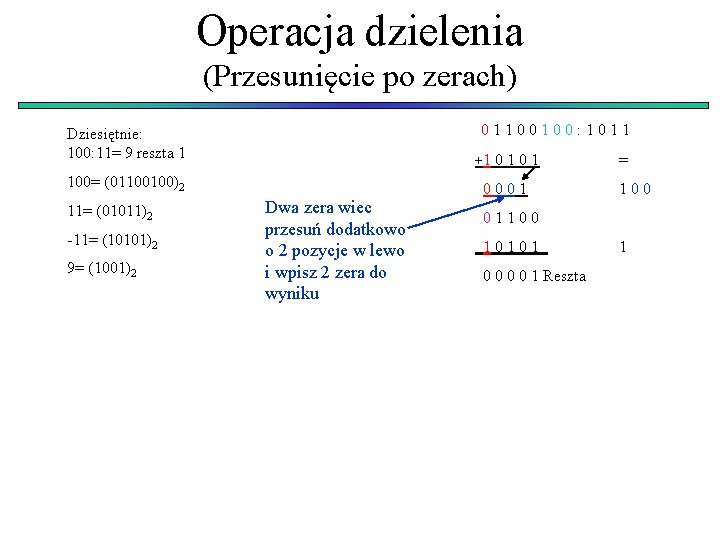
Operacja dzielenia (Przesunięcie po zerach) 01100100: 1011 Dziesiętnie: 100: 11= 9 reszta 1 +1 0 1 100= (01100100)2 11= (01011)2 -11= (10101)2 9= (1001)2 Dwa zera wiec przesuń dodatkowo o 2 pozycje w lewo i wpisz 2 zera do wyniku 0001 = 100 01100 10101 0 0 1 Reszta 1

Operacja dzielenia Przesunięcie po zerach Trzy najstarsze bity odejmowania (dzielnadzielnik): 010: wynik<<=1; wynik|=1; dzielna<<=1; 001: wynik<<=2; wynik|= 2; dzielna<<=2; 000: wynik<<=3; wynik|= 4; dzielna<<=3; 1 xx: wynik<<=1; dzielna<<=1; Przesunięcie o więcej niż jeden bit w momencie kiedy wynik odejmowania wskazuje, że Dzielnik > 2*Dzielna lub Dzielnik> 4*Dzielna Uwaga: argumenty muszą być znormalizowane na samym początku

Operacja dzielenia Radix 4 Multiplekser: If (w 3>=0) then w= w 3 Else if (w 2>=0) then w=w 2 Else if (w 1>=0) then w= w 1 Else w= w 0

Operacja dzielenia: Newton-Raphson Znajdowanie miejsca zerowego funkcji: Nachylenie stycznej w danym punkcie, f(Xi+1)=0 Przekształcając otrzymujemy Szukamy miejsca zerowego funkcji: Rozwiązanie (miejsce zerowe): X= 1/D Pochodna f ’(X)= 1/X 2

Dzielenie: metoda Newtona – Raphsona Przykład: dzielenie przez 3, D=3 x 0= 0. 5 x 1= 0. 5(2 - 0. 5· 3)= 0. 25 x 2= 0. 3125 x 3= 0. 33203125 x 4= 0. 333328247 x 5= 0. 33333 Każda iteracja podwaja liczbę poprawnych bitów wyniku

Newton-Raphson c. d. : • Określić wartość wstępną x 0 = 1/b np. za pomocą LUT i odpowiednich przesunięć • Iteracyjnie obliczyć xi+1 = xi(2 -xib) aż do punktu zbieżności (w n krokach). Proces iteracyjny jest tym szybciej zbieżny im wartość początkowa x 0 poszukiwanego rozwiązania jest bliższa wartości rzeczywistej x. Wymagana liczba iteracji, n, zależy od tego, z jaką precyzją obliczenia mają zostać wykonane. Należy przy tym pamiętać, że każdy następny krok iteracji podwaja ilość poprawnych bitów w wyniku. Można założyć, że po czterech iteracjach jesteśmy w stanie obliczyć odwrotność z dokładnością do 16 bitów. A po 5 iteracjach z dokładnością 32 bitów.

Newton-Raphson c. d. FF – rejestry (ang. Flip-Flops)

Pierwiastek kwadratowy Newton-Raphson Szybkość aproksymowania kwadratowa (liczba ważnych bitów podwaja się w każdej iteracji) Wada: - używanie operacji dzielenia

Pierwiastek kwadratowy bez operacji dzielenia Miejsce zerowe funkcji: Wynikiem powyższej iteracji XK jest dlatego aby otrzymać bezpośrednio pierwiastek należy przeprowadzić operację dzielenia lub co jest zalecane mnożenia:

Taylor-Maclaurin Ogólna postać: f(x)= a 0+ a 1 x + a 2 x 2 + a 3 x 3 +. . Postać ulepszona (nie trzeba obliczać xn) (metoda Horner’a): f(x)= b 0+ x·(b 1 + x·(b 2 + x·(b 3 +. . . ) ) )

Różne metody wyznaczania współczynników wielomianu Wykres błędu aproksymacji dla różnych metod wyznaczania współczynników wielomianu aproksymującego - dla funkcji ln(x), x=[1, 2) i wielomianu rzędu 3. Na wykresie jest podany maksymalny błąd dla różnych metod funkcja Matlab’a: Minimax(Function, Interval, Degree) Minimax – optymalizacja w celu osiągnięcia najmniejszego błędu w najgorszym przypadku

Wielomiany Czebyszewa T 0(x) = 1 T 1(x) = x T 2(x) = 2 x 2 -1 T 3(x) = 4 x 3 -3 x T 4(x) = 8 x 4 -8 x 2+1 T 5(x) = 16 x 5 -20 x 3+5 x T 6(x) = 32 x 6 -48 x 4+18 x 2 -1.

Redukcja dziedziny wejściowej 1) Redukcja zakresu danej wejściowej do mniejszego zakresu 2) Obliczanie funkcji dla zredukowanego przedziału 3) Rekonstrukcja funkcji dla całego przedziału wejściowego 4) Przykład: 5) Funkcja przedział x rekonstrukcja [0, /2) sin(x+k )= (-1)k sin(x), sin( -x)= 7) 2 x całkowita X [0, 1) 2 X= 2 Xint 2 x 8) ln(x) [1, 2) ln(X)= Xint ln(2) +ln(x) 9) x (0. 25, 1] (22 i x)= 2 i x 6) sin(x) Xint- część

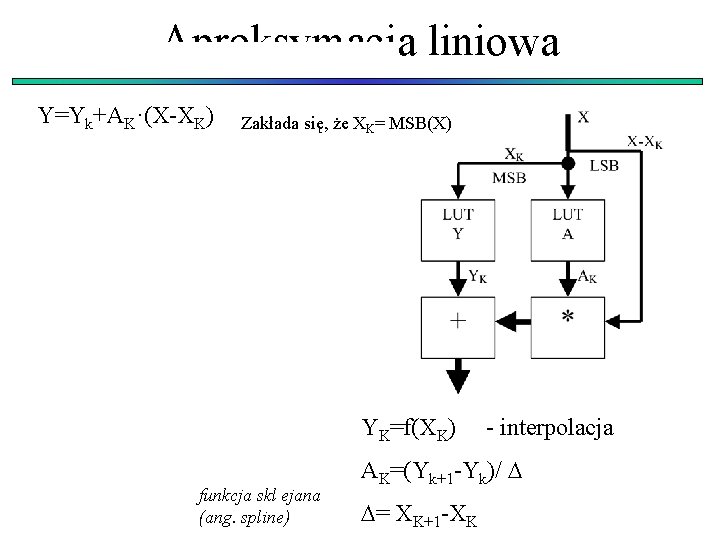
Aproksymacja liniowa Y=Yk+AK·(X-XK) Zakłada się, że XK= MSB(X) YK=f(XK) funkcja skl ejana (ang. spline) - interpolacja AK=(Yk+1 -Yk)/ = XK+1 -XK

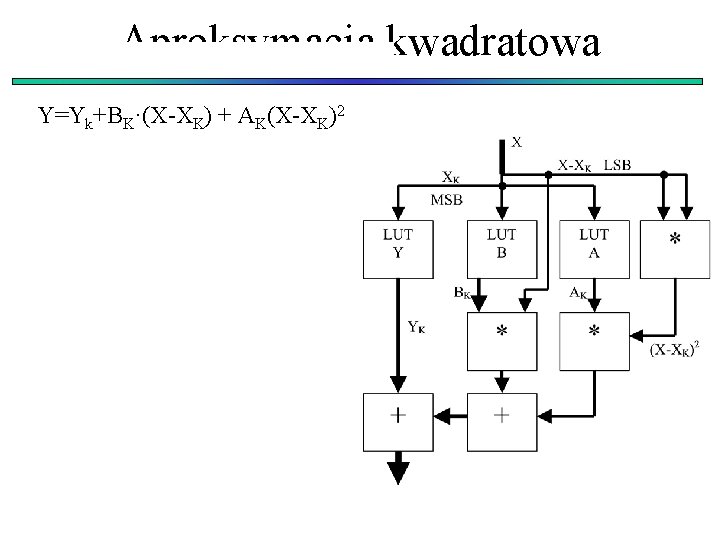
Aproksymacja kwadratowa Y=Yk+BK·(X-XK) + AK(X-XK)2

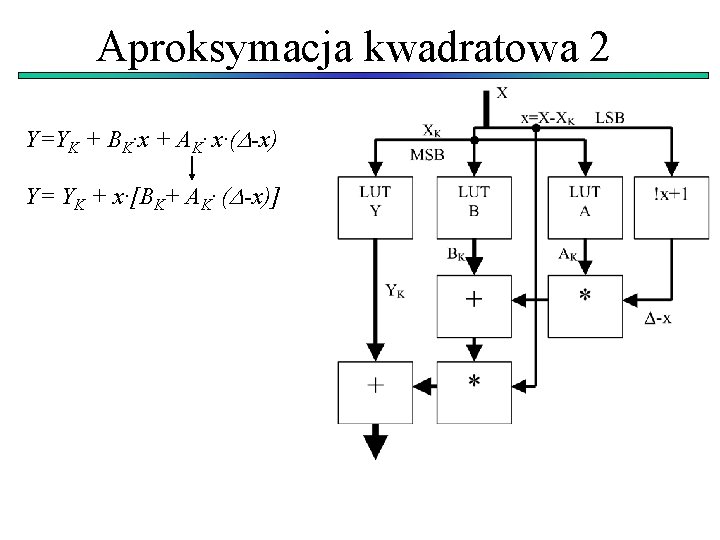
Aproksymacja kwadratowa 2 Inne rozwiązanie: Y=YK + BK·(X-XK) + AK· (X-XK)·(XK+1 -X) = XK+1 -XK X=XK + x Y=YK + BK·x + AK· x·( -x) Wartości współczynników: YK=f(XK) BK=(Yk+1 -Yk)/ Założenie przy obliczaniu AK: f(XK+ /2)= Y(XK+ /2) f(XK+ /2)= YK+BK · /2+AK ·( /2)2

Aproksymacja kwadratowa 2 Y=YK + BK·x + AK· x·( -x) Y= YK + x·[BK+ AK· ( -x)]