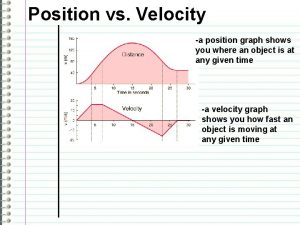
PHY 151 Lecture 3 3 1 Position Velocity
























































- Slides: 66

PHY 151: Lecture 3 Ø 3. 1 Position, Velocity, and Acceleration Vectors Ø 3. 2 Two-Dimensional Motion with Constant Acceleration Ø 3. 3 Projectile Motion Ø 3. 4 Particle in Uniform Circular Motion Ø 3. 5 Tangential and Radial Acceleration Ø 3. 6 Relative Velocity and Acceleration Ø 3. 7 Context Connection: Lateral Acceleration of Automobiles

PHY 151: Lecture 3 Motion in Two Dimensions 3. 1 Position, Velocity, and Acceleration Vectors

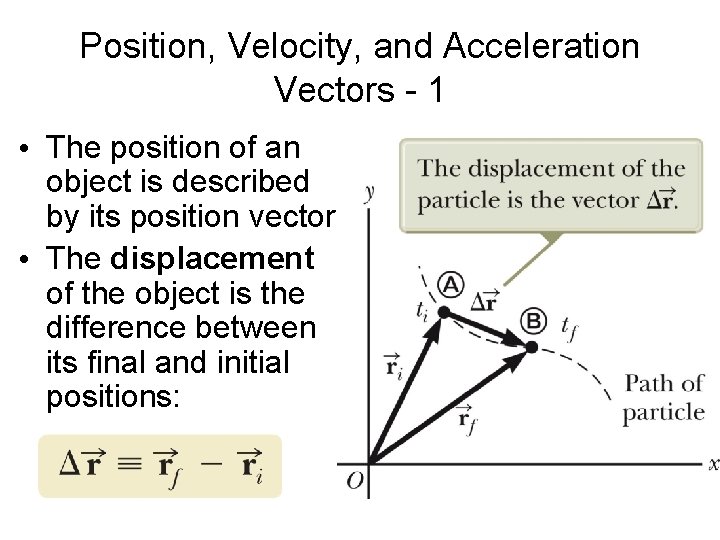
Position, Velocity, and Acceleration Vectors - 1 • The position of an object is described by its position vector • The displacement of the object is the difference between its final and initial positions:

Position, Velocity, and Acceleration Vectors - 3 • The average velocity between points is independent of the path taken • This is because it is dependent on the displacement, which is also independent of the path • If a particle starts its motion at some point and returns to this point via any path, its average velocity is zero for this trip since its displacement is zero

Position, Velocity, and Acceleration Vectors - 4 • The instantaneous velocity is the limit of the average velocity as ∆t approaches zero: • The direction of the instantaneous velocity vector at any point in a particle’s path is along a line tangent to the path at that point and in the direction of motion – The magnitude of the instantaneous velocity vector is the speed

Position, Velocity, and Acceleration Vectors - 5 • The average acceleration of a particle is the ratio of the change in the instantaneous velocity to the time interval:

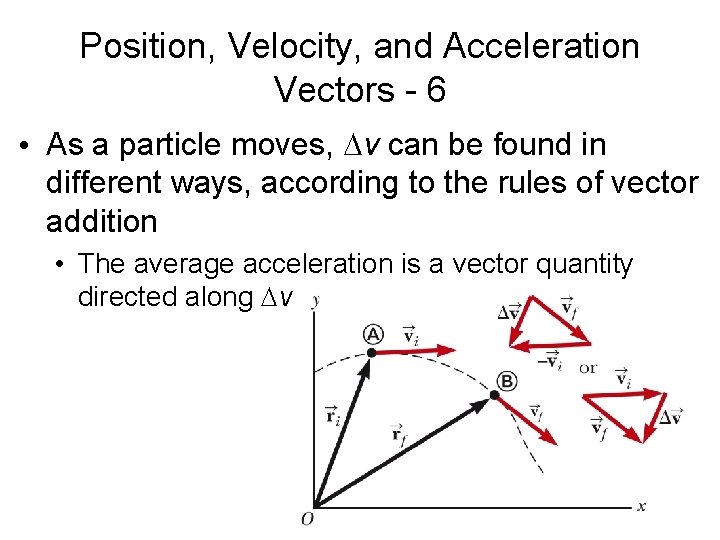
Position, Velocity, and Acceleration Vectors - 6 • As a particle moves, v can be found in different ways, according to the rules of vector addition • The average acceleration is a vector quantity directed along v

Position, Velocity, and Acceleration Vectors - 7 • The instantaneous acceleration is the limit of the average acceleration as v/ t approaches zero:

Position, Velocity, and Acceleration Vectors - 8 • Various changes in a particle’s motion may produce an acceleration – The magnitude of the velocity vector may change – The direction of the velocity vector may change • Even if the magnitude remains constant – Both may change simultaneously

PHY 151: Lecture 3 Motion in Two Dimensions 3. 2 Two-Dimensional Motion with Constant Acceleration

Two-Dimension Motion With Constant Velocity - 1 • When the two-dimensional motion has a constant acceleration, a series of equations can be developed that describe the motion • These equations will be similar to those of onedimensional kinematics • Motion in two dimensions can be modeled as two independent motions in the x and y directions • Any influence in the y direction does not affect the motion in the x direction, and vise versa

Two-Dimension Motion with Constant Velocity - 2 • Position vector: • Velocity: • Since acceleration is constant, we can also find an expression for the velocity as a function of time: • The position vector as a function of time can be written as

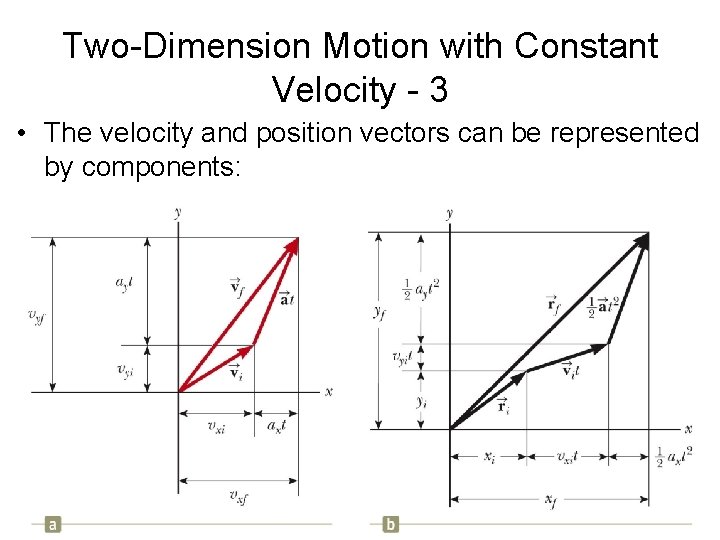
Two-Dimension Motion with Constant Velocity - 3 • The velocity and position vectors can be represented by components:

Example 3. 1 A particle moves in the xy plane, starting from the origin at t = 0 with an initial velocity having an x component of 20 m/s and a y component of 15 m/s. The particle experiences an acceleration in the x direction, given by ax = 4. 0 m/s 2.

Example 3. 1 (A) Determine the total velocity vector at any time. Set vxi = 20 m/s; vyi = 15 m/s; ax = 4. 0 m/s 2; ay = 0 • Find the velocity vector: • Substitute numerical values:

Example 3. 1 (B) Calculate the velocity and speed of the particle at t = 5. 0 s and the angle the velocity vector makes with the x axis. • Evaluate the result from Equation (1) at t = 5. 0 s: • Determine that angle: • Evaluate the speed:

Example 3. 1 (C) Determine the x and y coordinates of the particle at any time t and its position vector at this time. • Use xi = yi = 0 at t = 0: • Express the position vector of the particle at any time t:

PHY 151: Lecture 3 Motion in Two Dimensions 3. 3 Projectile Motion

Projectile Motion - 1 • An object may move in both the x and y directions simultaneously • The form of two-dimensional motion we will deal with is called projectile motion • Assumptions: (1) the free-fall acceleration g is constant over the range of motion and directed downward (2) the effect of air resistance is negligible 0

Projectile Motion - 2 • With these assumptions, an object in projectile motion will follow a parabolic path • This path is called the trajectory

Projectile Motion - 3 • Reference frame chosen: • y is vertical with upward positive • Acceleration components: ay = g and ax = 0 • Initial velocity components: vxi = vi cos q and vyi = vi sin q

Projectile Motion - 4 • The velocity components and position coordinates for the projectile at any time t are • The expression for the trajectory of a projectile is (valid for angles in the range 0 < i < /2)

Projectile Motion - 5 • The vector expression for the position of a projectile as a function of time is • The final position is the vector sum of the initial position, the position resulting from the initial velocity, and the position resulting from the acceleration

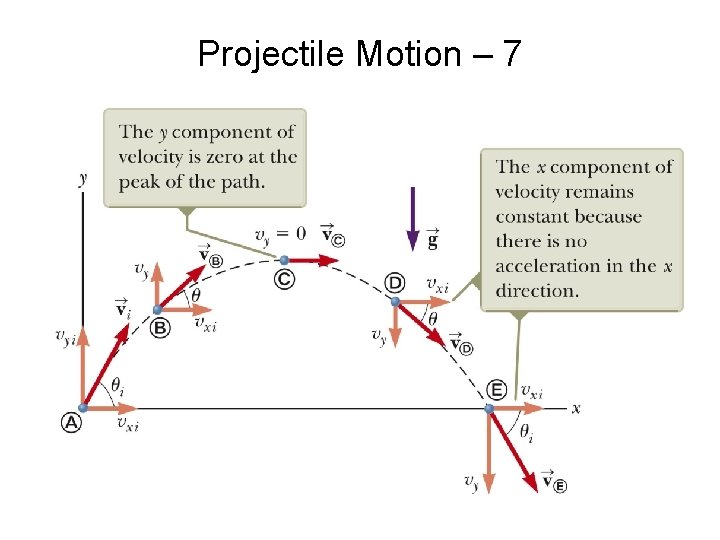
Projectile Motion – 7

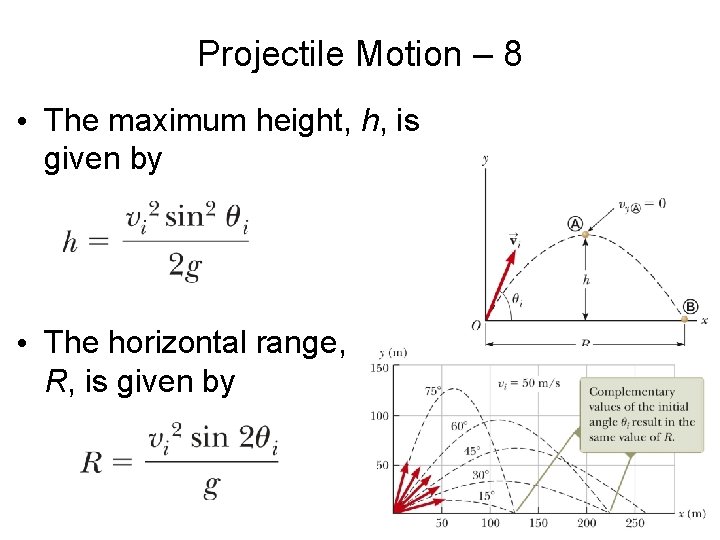
Projectile Motion – 8 • The maximum height, h, is given by • The horizontal range, R, is given by

Projectile Motion – 9 • The maximum range occurs at qi = 45 o • Complementary angles will produce the same range • The maximum height will be different for the two angles • The times of the flight will be different for the two angles

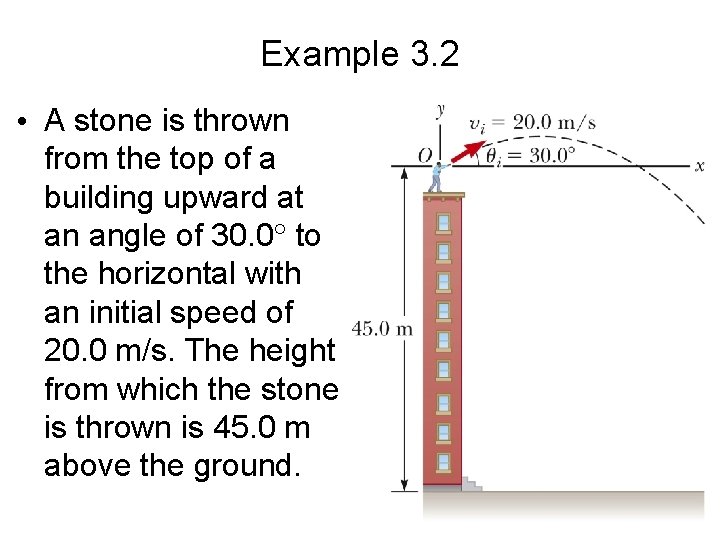
Example 3. 2 • A stone is thrown from the top of a building upward at an angle of 30. 0 to the horizontal with an initial speed of 20. 0 m/s. The height from which the stone is thrown is 45. 0 m above the ground.

Example 3. 2 (A) How long does it take the stone to reach the ground? – We have: xi = yi = 0; yf = 45. 0 m; ay = g; vi = 20 m/s – Find the initial x and y components of the stone’s velocity: – Express the vertical position of the stone:

Example 3. 2 – Substitute numerical values: – Solve the quadratic equation for t:

Example 3. 2 (B) What is the speed of the stone just before it strikes the ground? • Find the y component of the velocity just before it strikes the ground: • Substitute numerical values, using t = 4. 22 s: • Find the speed of the stone:

Example 3. 3 A ski jumper leaves the ski track moving in the horizontal direction with a speed of 25. 0 m/s. The landing incline below her falls off with a slope of 35. 0. Where does she land on the incline?

Example 3. 3 • • • Express the coordinates of the jumper as a function of time: Substitute the values of xf and yf at the landing point: Solve Equation (3) for t and substitute the result into equation (4):

Example 3. 3 – Solve for d: – Evaluate the x and y coordinates of the point at which the skier lands:

Example 3. 4 – An athlete throws a javelin a distance of 80. 0 m at the Olympics held at the equator, where g = 9. 78 m/s 2. Four years later the Olympics are held at the North Pole, where g = 9. 83 m/s 2. Assuming that the thrower provides the javelin with exactly the same initial velocity as she did at the equator, how far does the javelin travel at the North Pole?

Example 3. 4 – Express the range of the particle at each of the two locations: – Divide the first equation by the second to establish a ratio between the ratio of the ranges and the ratio of the free-fall accelerations:

Example 3. 4 • Solve the equation for the range at the North Pole and substitute values:

Projectile Motion – Example 1 a • • Ball with horizontal speed of 1. 5 m/s rolls off bench 2. 0 m high (a) How long will it take the ball to reach floor? Ø Horizontal xf = xi + vt xi = 0 xf = ? v = 1. 5 t=? xf = 0 + 1. 5 t Equation has 2 unknowns xf, t Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 2 yf = 0 vi = 0 vf = ? a = -9. 8 t = ? vf = 0 – 9. 8 t Equation has 2 unknowns, vf, t 0 = 2 + 0 t + ½(-9. 8)t 2 Equation has 1 unknown, t 02 = 402+2(-9. 8)(yf– 100) Equation has 1 unknown, yf 0 = 2 + 0 t + ½(-9. 8)t 2 t = sqrt(-4/-9. 8) = 0. 64 s

2 -Dimensions Projectile Motion – Example 1 b • Ball with horizontal speed of 1. 5 m/s rolls off bench 2. 0 m high • How far from point on floor directly below edge of the bench will ball land? Ø Horizontal xf = xi + vt xi = 0 xf = ? v = 1. 5 t = 0. 64 xf = 0 + 1. 5(0. 64) Equation has 1 unknown, xf = 0 + 1. 5(0. 64) = 0. 96 m

2 -Dimensions Projectile Motion – Example 2 (Find Time) • Ball rolls horizontally with speed of 7. 6 m/s off edge of tall platform • Ball lands 8. 7 m from the point on ground directly below edge of platform • What is height of platform? Ø Horizontal xf = xi + vt xi = 0 xf = 8. 7 v = 7. 6 t = ? 8. 7 = 0 + 7. 6 t t = 8. 7 / 7. 6 = 1. 14 s Equation has 1 unknown, t

Projectile Motion – Example 2 (Find Height) • Ball rolls horizontally with speed of 7. 6 m/s off edge of tall platform • Ball lands 8. 7 m from point on ground directly below platform • What is height of platform? Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = ? yf = 0 vi = 0 vf = ? a = -9. 8 t = 1. 14 vf = 0 – 9. 8(1. 14) Equation has 1 unknown, vf 0 = yi + 0(1. 14) + ½(-9. 8)(1. 14)2 Equation has 1 unknown, yi vf 2 = 02+2(-9. 8)(yf–yi) Equation has 3 unknowns, yi, yf, vf 0 = yi + 0(1. 14) + ½(-9. 8)(1. 14)2 yi =-(1/2)(-9. 8)(1. 14)2 = 6. 37 m

Projectile Motion – Example 3 a • • A rifle fires a bullet at a speed of 250 m/s at an angle of 370 above the horizontal. (a) What height does the bullet reach? Ø Horizontal Ø xf = xi + vt xi = 0 v=250 cos(37)=199. 7 xf = 0 + 199. 7 t Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 vi = 250 sin(37)=150. 5 a = -9. 8 0 = 150. 5 – 9. 8 t yf = 0 + 150. 5 t + ½(-9. 8)t 2 02 = 150. 52+2(-9. 8)(yf– 0) yf =-150. 52/2/-9. 8 = 1155 m xf = ? t=? Equation has 2 unknowns, xf, t yf = ? vf = 0 t=0 Equation has 1 unknown, t Equation has 2 unknowns, yf, t Equation has 1 unknown, yf

Projectile Motion – Example 3 b • • A rifle fires a bullet at a speed of 250 m/s at an angle of 370 above the horizontal. (b) How long is the bullet in the air? Ø Horizontal xf = xi + vt xi = 0 xf = ? v=250 cos(37)=199. 7 t = ? xf = 0 + 199. 7 t Equation has xf, t Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 0 vi = 250 sin(37)=150. 5 vf = ? a = -9. 8 t=? vf = 150. 5 – 9. 8 t Equation has 2 unknowns, vf, t 0 = 0 + 150. 5 t + ½(-9. 8)t 2 Equation has 1 unknown, t vf 2 = 150. 52+2(-9. 8)(0– 0) Equation has 1 unknown, vf 0 = 0 + 150. 5 t + ½(-9. 8)t 2 t = -150. 5(2)/-9. 8 = 30. 7 s

Projectile Motion – Example 3 c • • A rifle fires a bullet at a speed of 250 m/s at an angle of 370 above the horizontal. (b) What is the balls range? Ø Horizontal xf = xi + vt xi = 0 xf = ? v=250 cos(37)=199. 7 t = 30. 7 xf = 0 + 199. 7(30. 7) Equation has 1 unknown, xf Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 0 vi = 250 sin(37)=150. 5 vf = ? a = -9. 8 t = 30. 7 vf = 150. 5 – 9. 8(30. 7) Equation has 1 unknown, vf 0=0+150. 5(30. 7)+½(-9. 8)(30. 7)2 Can’t use equation vf 2 = 150. 52+2(-9. 8)(0– 0) Equation has 1 unknown, vf xf = 0 + 199. 7(30. 7) = 6130. 8 m

2 -Dimension Projectile Motion – Example 4 a (Find Time) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 9 degrees to the horizontal • (a) Find height at which it hits fence at distance 180 m? • Horizontal xf = xi + vt xi = 0 xf = 180 v = 50 cos 36. 9 = 40 t = ? 180 = 0 + 40 t t = 180 / 40 = 4. 5 s Equation has 1 unknown, t

Projectile Motion – Example 4 a (Find Height) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 9 degrees to the horizontal • (a) Find height at which it hits fence at distance 180 m? Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = ? vi = 50 sin 36. 9=30 vf = ? a = -9. 8 t = 4. 5 vf = 30 – 9. 8(4. 5) Equation has 1 unknown, vf yf = 0 + 30(4. 5) + ½(-9. 8)(4. 5)2 Equation has 1 unknown, yi vf 2 = 302+2(-9. 8)(yf – 0) Equation has 2 unknowns, yf, vf yf = 0 + 30(4. 5) + ½(-9. 8)(4. 5)2 = 35. 8 m

2 -Dimensions Projectile Motion – Example 4 b (Find Velocity 1) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 9 degrees to the horizontal • (b) What is velocity at which it hits a fence at distance of 180 m? Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 35. 8 vi = 50 sin 36. 9=30 vf = ? a = -9. 8 t = 4. 5 vf = 30 – 9. 8(4. 5) Equation has 1 unknown, vf 35. 8 = 0 + 30(4. 5) + ½(-9. 8)(4. 5)2 Can’t use equation vf 2 = 302+2(-9. 8)(35. 8 – 0) Equation has 1 unknown, vf = 30 – 9. 8(4. 5) = -14. 1 m/s

2 -Dimensions Projectile Motion – Example 4 b (Find Velocity 2) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 90 to the horizontal • (b) What is velocity at which it hits a fence at distance of 180 m? Øvy = -14. 1 m/s Øvx = 40 Øv = sqrt(402 + (-14. 1)2) = 42. 4 m/s Øq = tan-1(14. 1/40) = 19. 10 Øvy is negative, therefore points into fourth quadrant

PHY 151: Lecture 3 Motion in Two Dimensions 3. 4 Particle in Uniform Circular Motion

Particle in Uniform Circular Motion - 1 • Uniform circular motion occurs when an object moves in a circular path with a constant speed • An acceleration exists since the direction of the motion is changing • This change in velocity is related to an acceleration • The velocity vector is always tangent to the path of the object

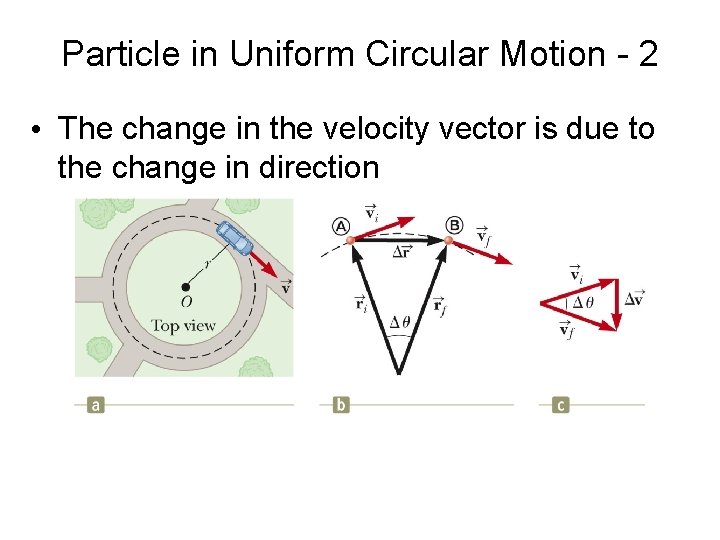
Particle in Uniform Circular Motion - 2 • The change in the velocity vector is due to the change in direction

Particle in Uniform Circular Motion - 3 • The acceleration is always perpendicular to the path of the motion • The acceleration always points toward the center of the circle of motion • This acceleration is called the centripetal acceleration • Centripetal means center-seeking

Particle in Uniform Circular Motion - 4 • The magnitude of the centripetal acceleration vector is given by • The direction of the centripetal acceleration vector is always changing, to stay directed toward the center of the circle of motion

Particle in Uniform Circular Motion – 5 • The period, T, is the time interval required for one complete revolution • The speed of the particle would be the circumference of the circle of motion divided by the period • Therefore, the period is

Example 3. 5 What is the centripetal acceleration of the Earth as it moves in its orbit around the Sun? – The period of the Earth’s orbit is 1 year, and its orbital radius is 1. 496× 1011 m – Substitute numerical values:

PHY 151: Lecture 3 Motion in Two Dimensions 3. 5 Tangential and Radial Acceleration

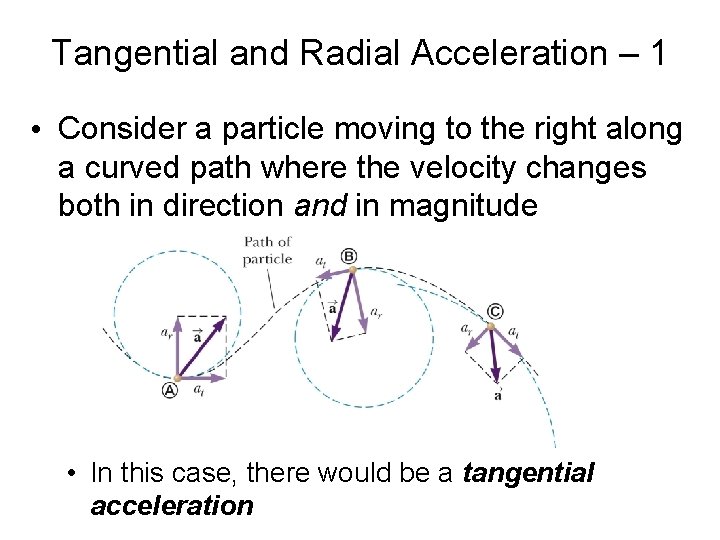
Tangential and Radial Acceleration – 1 • Consider a particle moving to the right along a curved path where the velocity changes both in direction and in magnitude • In this case, there would be a tangential acceleration

Tangential and Radial Acceleration – 2 • The total acceleration is: – The tangential acceleration causes a change in speed of the particle: – The radial acceleration comes from a change in the direction of the velocity vector:

PHY 151: Lecture 3 Motion in Two Dimensions 3. 6 Relative Velocity and Relative Acceleration Skipped

Relative Velocity and Acceleration – 1 • Consider the two observers A and B along the number line. – observer A is located at the origin – observer B is at the position x. A = 5 – We denote the position variable as x. A because observer A is at the origin of this axis – Both observers measure the position of point P, which is located at x. A = +5

Relative Velocity and Acceleration – 2 • Suppose observer B decides that he is located at the origin of an x. B axis • The two observers disagree on the value of the position of point P – Observer A claims point P is located at a position with a value of +5 – Observer B claims it is located at a position with a value of +10

Relative Velocity and Acceleration – 3 • Both observers are correct, even though they make different measurements • Their measurements differ because they are making the measurement from different frames of reference

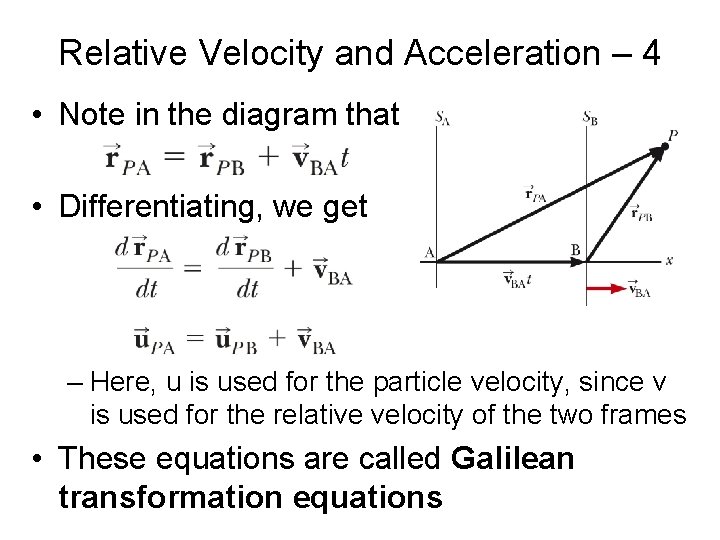
Relative Velocity and Acceleration – 4 • Note in the diagram that • Differentiating, we get – Here, u is used for the particle velocity, since v is used for the relative velocity of the two frames • These equations are called Galilean transformation equations

Relative Velocity and Acceleration – 5 • Even though observers in two frames measure different velocities, they measure the same acceleration when relative velocity between the two frames is constant:

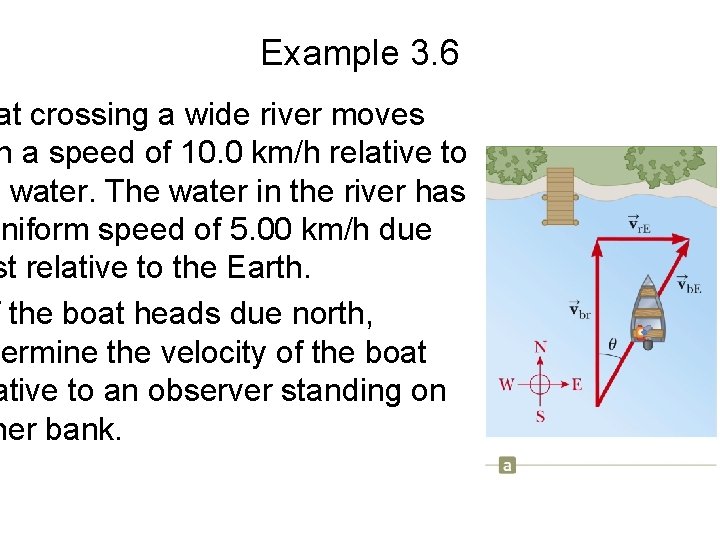
Example 3. 6 at crossing a wide river moves h a speed of 10. 0 km/h relative to e water. The water in the river has uniform speed of 5. 00 km/h due st relative to the Earth. f the boat heads due north, termine the velocity of the boat ative to an observer standing on her bank.

Example 3. 6

Example 3. 6 • Find the speed using the Pythagorean theorem: • Find the direction:
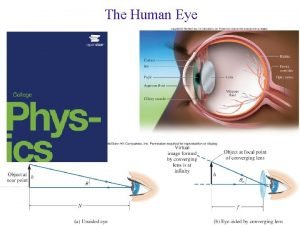
 What is farsightedness called
What is farsightedness called Ballet terms and positions
Ballet terms and positions 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Darcy law example
Darcy law example Final velocity initial velocity acceleration time
Final velocity initial velocity acceleration time Tangential speed
Tangential speed Difference between permeability and hydraulic conductivity
Difference between permeability and hydraulic conductivity Speed time graph
Speed time graph Angular acceleration formula
Angular acceleration formula Angular quantities
Angular quantities Instantaneous velocity vs average velocity
Instantaneous velocity vs average velocity Initial velocity and final velocity formula
Initial velocity and final velocity formula Phy circuit
Phy circuit Atm packet phy
Atm packet phy Ddr phy architecture
Ddr phy architecture Physics 2048
Physics 2048 Complete motion diagram
Complete motion diagram Phy
Phy Phy 231 msu
Phy 231 msu Phy theorem
Phy theorem Phy tgen
Phy tgen Phy 132
Phy 132 General physics
General physics Fizik ii
Fizik ii Phy 1214
Phy 1214 Phy 205
Phy 205 Physics heat and temperature
Physics heat and temperature Felix connects a wire coil to an ammeter
Felix connects a wire coil to an ammeter Phy
Phy Phy113
Phy113 Great orthogonality theorem proof
Great orthogonality theorem proof 2012 phy
2012 phy Phy
Phy Phy 2049
Phy 2049 Nearsighted diverging lens
Nearsighted diverging lens Phy 1214
Phy 1214 General physics measurement
General physics measurement Life phy
Life phy Phy
Phy Phy 131 asu
Phy 131 asu Phy-105 5 discussion
Phy-105 5 discussion Phy 110
Phy 110 General physics
General physics Phy 2049
Phy 2049 Phy 131 past papers
Phy 131 past papers Phy 221 msu
Phy 221 msu Phy108
Phy108 Vx=vox+axt
Vx=vox+axt Angular position velocity and acceleration
Angular position velocity and acceleration Constant velocity position time graph
Constant velocity position time graph Is velocity derivative of position
Is velocity derivative of position What does constant acceleration mean
What does constant acceleration mean Mozzanica antincendio
Mozzanica antincendio Tổng kết vốn từ 151
Tổng kết vốn từ 151 Software consists of...
Software consists of... Freeze concentration
Freeze concentration Model-netics 151 models
Model-netics 151 models Econ 151
Econ 151 Item 151
Item 151 118/151
118/151 Mcb 101 uiuc
Mcb 101 uiuc Conforme a tua infinita graça numero
Conforme a tua infinita graça numero Sjsu cs 151
Sjsu cs 151 Apsc 151
Apsc 151 Cs 175 uci
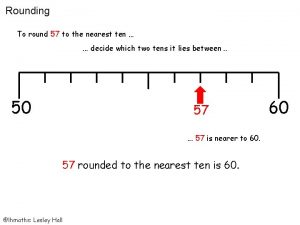
Cs 175 uci Round 57 to the nearest 10
Round 57 to the nearest 10 The equilibrium level of real gdp
The equilibrium level of real gdp