Velocity Velocity is the derivative of position with

Velocity • Velocity is the derivative of position with respect to time. – Linear V – Angular w • Velocity vector is associated with a point in space. • Velocities are relative to reference frames. – Train, Car, Fixed • Speed is the magnitude of the velocity without direction information. • Velocity contains information on direction and magnitude. Robotics II Copyright Martin P. Aalund, Ph. D.

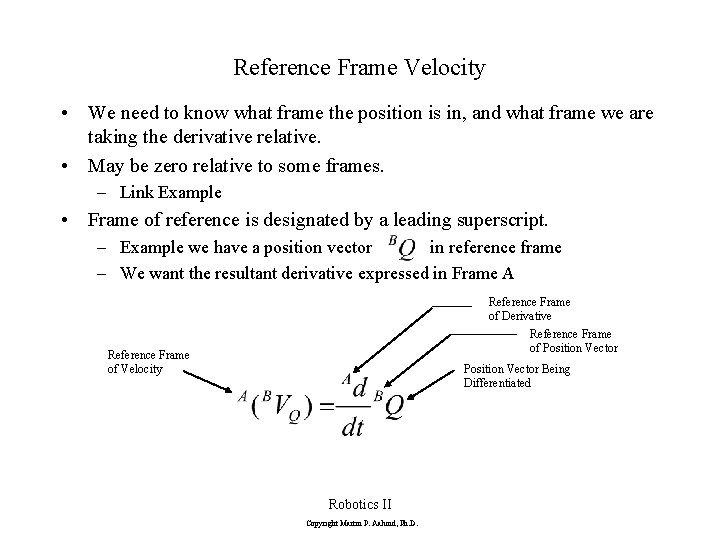
Reference Frame Velocity • We need to know what frame the position is in, and what frame we are taking the derivative relative. • May be zero relative to some frames. – Link Example • Frame of reference is designated by a leading superscript. – Example we have a position vector in reference frame – We want the resultant derivative expressed in Frame A Reference Frame of Derivative Reference Frame of Position Vector Reference Frame of Velocity Position Vector Being Differentiated Robotics II Copyright Martin P. Aalund, Ph. D.

Reference Frames Velocity • If A and B are the same we drop the outer superscript • We can always remove the outer superscript by including the rotation matrix. • We will often consider the velocity of the origin of a frame {C} relative to an understood universal reference {U} • Or expressed in Frame {A} but still differentiated in {U} Robotics II Copyright Martin P. Aalund, Ph. D.

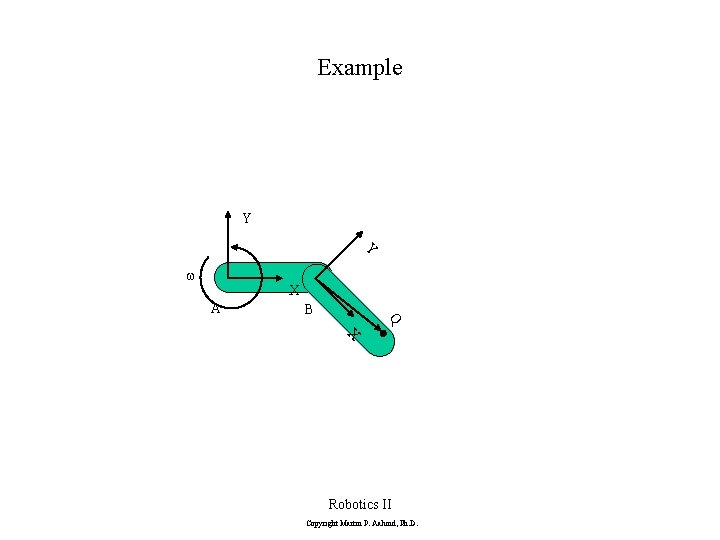
Example Y Y w X A B Q X Robotics II Copyright Martin P. Aalund, Ph. D.

Angular Velocity • Describes the motion of a frame or a body in space. W • Definition Frame measured Relative Angular Velocity of Frame being measured Angular Velocity of Frame C relative to Global Coordinate Frame • The direction of AWB represents the instantaneous axes of rotation of frame {B} relative to frame {A}. • The magnitude represents the angular speed of rotation. • Can be expressed in any frame Robotics II Copyright Martin P. Aalund, Ph. D.

Linear and Rotational Frames in Rigid Bodies Robotics II Copyright Martin P. Aalund, Ph. D.

Motion of Rigid Bodies • First attach a reference frame to each body • Now we can study the motion of each frame relative to the next. • The is the same methodology we used to study the forward position of the manipulator. • Lets look at frame {A} and {B} BQ {A} Robotics II Copyright Martin P. Aalund, Ph. D.

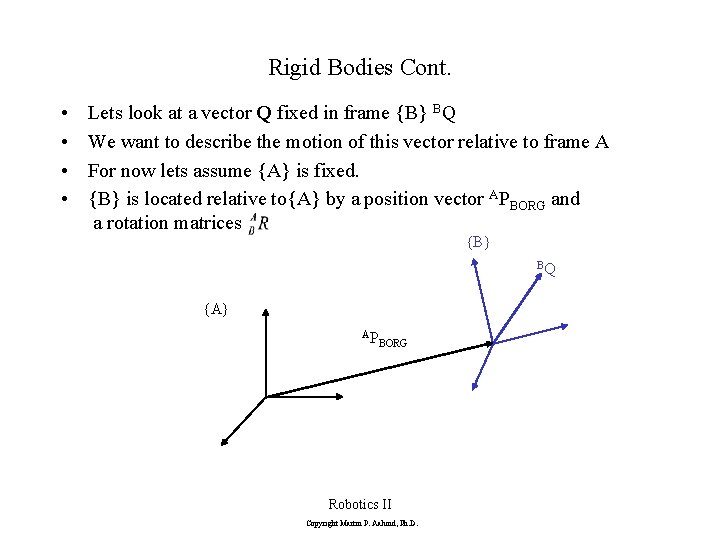
Rigid Bodies Cont. • • Lets look at a vector Q fixed in frame {B} BQ We want to describe the motion of this vector relative to frame A For now lets assume {A} is fixed. {B} is located relative to{A} by a position vector APBORG and a rotation matrices {B} BQ {A} AP BORG Robotics II Copyright Martin P. Aalund, Ph. D.

Rigid Bodies Linear Motion • Three things can be in motion or changing with respect to time – The vector APBORG can be changing – The vector BQ can be changing – The orientation of {B} with respect to {A} may be changing. • First lets look at linear motion, so assume is not changing. • So we need only represent both velocity components in terms of {A} • Remember the velocity of Q is just a vector so we can use a standard rotation matrices to transform its value from one frame to another. • If we know Q(t) and APBORG(t) we can differentiate and plug into the above equation. Robotics II Copyright Martin P. Aalund, Ph. D.

Rigid Bodies Rotational Motion • Now lets assume that Q is constant and fixed in B. BVQ=0 • Even though Q has no velocity relative to B it is clear it can still have motion relative to A • The the motion is due to two components – The vector APBORG changing – The orientation of {B} with respect to {A} changing in time AWB. – Lets look first at the change due to rotation {A} AW B Robotics II Copyright Martin P. Aalund, Ph. D. {B} BQ

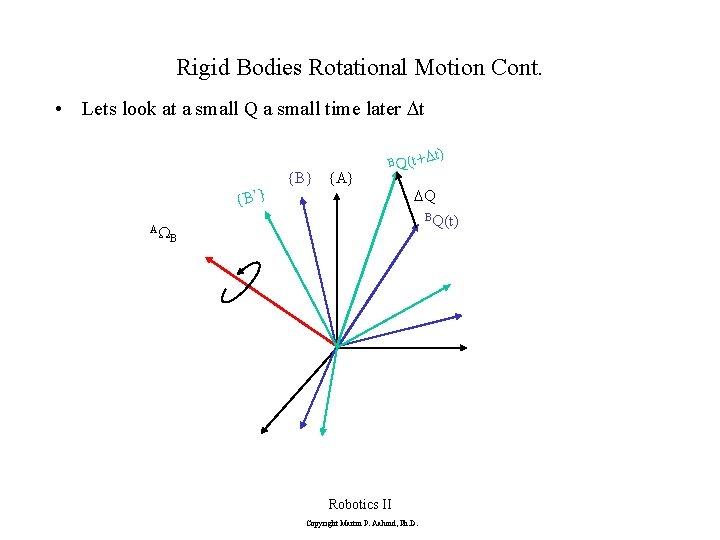
Rigid Bodies Rotational Motion Cont. • Lets look at a small Q a small time later Dt {B’} AW {B} {A} B Q(t+D t) DQ BQ(t) B Robotics II Copyright Martin P. Aalund, Ph. D.

Rigid Bodies Rotational Motion Cont. • The change in Q for a very small motion is just the radius times the change in the angle. Dt) + t Q( • Radius is Q sin(q) • Remember Q is not changing in time DQ • So DQ is just Q sin(q)WDt Q(t) AW • This is just the cross product of B Q and W If Q Changes with Time then q or in terms of {B} and R Robotics II Copyright Martin P. Aalund, Ph. D.

Simultaneous Linear and Rotational Motion • Linear • Rotational • Both Robotics II Copyright Martin P. Aalund, Ph. D.

Propagation Link to Link Rotational • So now that we can calculate the velocity of one body or reference frame relative to the other how do we apply this to a robot? • A robot is a chain of bodies represented by links that can rotate or translate relative to each other. • We already know how to assign a reference frame to each link. • The velocity of link i+1 is the velocity of link i, plus the velocity component added at joint i+1. • Angular velocities can be added if they are represented in the same frame. • Remember we have defined all joint motion to be around or along Z. Robotics II Copyright Martin P. Aalund, Ph. D.

Propagation Link to Link Rotational • For Linear velocity we get • This is the same as we previously derived with i. Pi+1 a constant. • If we want the velocity and angular velocity in terms of i+1 we simply pre-multiply by the rotation matrix. • Remember that the derivatives are still taken relative to a universal frame. So vi is the velocity of the origin of link frame{i} and wi is the angular velocity of link frame {i}. They can be expressed in any frame even frame {i}. Robotics II Copyright Martin P. Aalund, Ph. D.

Propagation for Translational Joints • Similarly for the case of a Translational joint we get • No additional angular velocity component since it’s a transnational joint. Just a change of reference frame. • But must add contribution due to linear motion of joint along Z axes Robotics II Copyright Martin P. Aalund, Ph. D.

Summary • We must apply the equations from link to link from along the chain until we determine the velocity of interest. • We can use the rotation matrices to move the velocity to any reference frame once we have it in a frame. • Rotation Joint • Translation Joint Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian • • What is a Jacobian Lets say we have a functions x=F(q 1, q 2) and y= G(q 1, q 2) We want to find the velocity vx and vy We use the chain rule to take the derivative • Or in matrix format Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Cont. • • The Jacobian is multi-dimensional form of the derivative At any instant the Jacobian is linear transformation. The Jacobian will vary as a function of time. Most common Jacobian deals with joint velocities. – It relates the Cartesian coordinates of the tip of the robot arm to the joint velocities or the derivatives of joint variables. • The number of rows corresponds to the number of joints • The number of columns corresponds to the number of Cartesian coordinates. • The most general form is a 6 x 6 matrix. Does not have to be square. • The Jacobian can be calculated for any orthogonal set of variables. – X, Y – R, q Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Cont • For low degree of freedom robots the Jacobian can be found by directly differentiating the equations of motion • This works for linear velocities but does not work for angular velocities. • Changing frame of reference of a Jacobian. • The general 6 x 6 Jacobian maps both the angular velocity vector and the linear velocity. If we view these two 3 x 1 vectors as one 6 x 1 vector we can see how we should change the Jacobian’s reference frame. Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Cont • We can use the following equation to convert from frame {B} to {A} • Since the Jacobian performs a similar mapping. • If the Jacobian is non singular we can invert it to find the joint rates in terms of the Cartesian coordinates. • What does a singular Jacobian mean. – In general it means that no instantaneous motion along one of the Cartesian coordinates is possible. Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Cont. • We can use the Jacobian to predict where these singularities occur • If we don’t check for singularities, we can end up commanding our joints to move at high velocities. • At the actual singularity we would require infinite motion from the joint. • Two common singularities occur – One is when two joints line up. – The second occurs at the edge of the workspace. • Additional singularities may exist that are not predicted by the Jacobian. • Structures can be designed to be singularity free from a Jacobian point of view. Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Example page 1 • Given the simple manipulator below find the Jacobian referenced to frame 4. Frame 4 is at the tip of the arm with the same orientation as frame 3 • The manipulator can be described by the transformation matrices (see Example 3. 3). Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Example page 2 • We are mapping from Cartesian to joint space • All Joints are revolutes so we can use Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Example page 3 • Propagating to get the velocity Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobian Example Page 4 • Answer • We could also have differentiated the position vector and then changed the reference frame. Robotics II Copyright Martin P. Aalund, Ph. D.

Static Forces in Manipulators • Want to know what are the joint torques required to push or hold something. – Assume the robot is stationary, lock the joints so it becomes a structure. – Do a force/moment balance in terms of link frames. – Compute static torques about the joint. • fi=force exerted on link i by link i-1 • ni=torque exerted on link i by link i-1 • For a force at the end of the robot we can propagate backwards • To calculate the toques of forces required of the joint only need Z component – For a Prismatic – For a Revolute Robotics II Copyright Martin P. Aalund, Ph. D.

Jacobean in Force Domain • Virtual Work – Based on conservation of energy. – Same amount of energy is required no mater what frame. – Work is the dot product of the force or torque vector and the motion vector. • – – F is the Cartesian force-moment vector x is an Cartesian displacement vector t is the joint toque-force vector Q is the joint position vector • The Jacobian is defined as: • So we can get the following Robotics II Copyright Martin P. Aalund, Ph. D.

Homework 1 • 5. 2 Show that you can get the same answer as the example in class by differentiating rather than propagation. • 5. 4 • 5. 7 • 5. 8 • 5. 13 • 5. 18 • 5. 20 • List 3 reasons for calculating the Jacobian. Robotics II Copyright Martin P. Aalund, Ph. D.