PHY 151 Lecture 5 5 1 Forces of























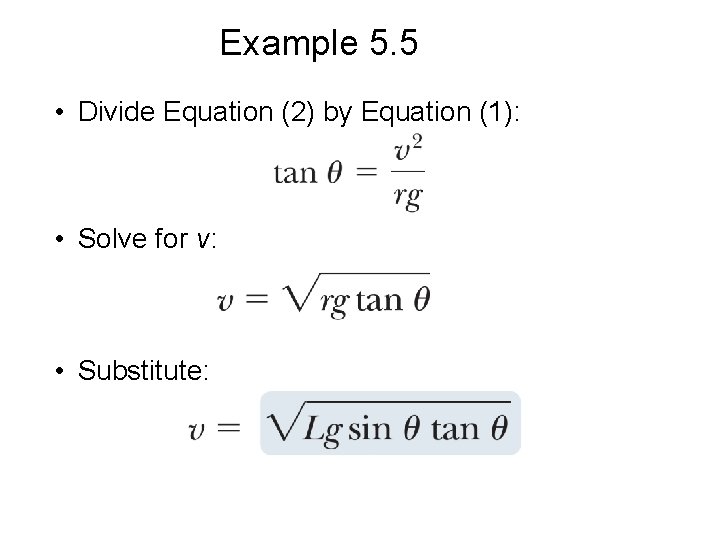


























































- Slides: 101

PHY 151: Lecture 5 • • 5. 1 Forces of Friction 5. 2 Particle in Uniform Circular Motion 5. 3 Nonuniform Circular Motion 5. 4 Motion in the Presence of Velocity Dependent Resistive Forces • 5. 5 The Fundamental Forces of Nature • 5. 6 Context Connection: Drag Coefficients of Automobiles

PHY 151: Lecture 5 More Applications of Newton’s Laws 5. 1 Forces of Friction

Forces of Friction - 1 • When an object moves or attempts to move on a surface or through a viscous medium, there will be a resistance to the motion • This is due to the interactions between the object and its environment • This resistance is called the force of friction

Forces of Friction - 2 • The force of static friction, ƒs, is generally greater than the force of kinetic friction, ƒk • The coefficient of friction (µ) depends on the surfaces in contact • Friction is proportional to the normal force ƒs £ µsn and ƒk= µkn – These equations relate the magnitudes of the forces, they are not vector equations

Forces of Friction - 3 • The direction of the frictional force is opposite the direction of motion and parallel to the surfaces in contact • The coefficients of friction are nearly independent of the area of contact

Forces of Friction - 4

Forces of Friction - 5 • The friction force arises from the nature of the two surfaces – because of their roughness, contact is made only at a few locations where peaks of the material touch • The friction force arises: – because one peak physically blocks the motion of a peak from the opposing surface – from chemical bonding (“spot welds”) of opposing peaks as they come into contact

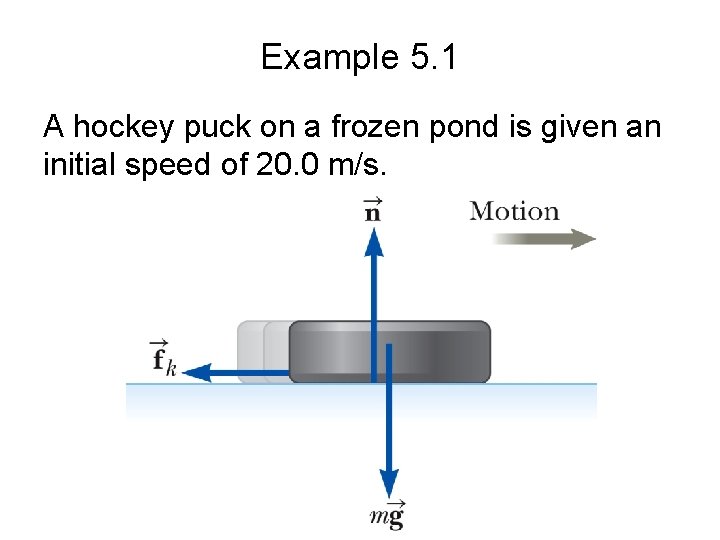
Example 5. 1 A hockey puck on a frozen pond is given an initial speed of 20. 0 m/s.

Example 5. 1 (A) If the puck always remains on the ice and slides 115 m before coming to rest, determine the coefficient of kinetic friction between the puck and ice. • Apply the particle under a net force model in the x direction to the puck: • Apply the particle in equilibrium model in the y direction to the puck:

Example 5. 1 • Substitute: • Apply the particle under constant acceleration model to the puck: • Solve for the coefficient of kinetic friction: • Substitute numerical values:

Example 5. 1 (B) If the initial speed of the puck is halved, what would be the sliding distance? • Solve Equation (3) in part (A) for xf 1 and xf 2: • Divide the first equation by the second:

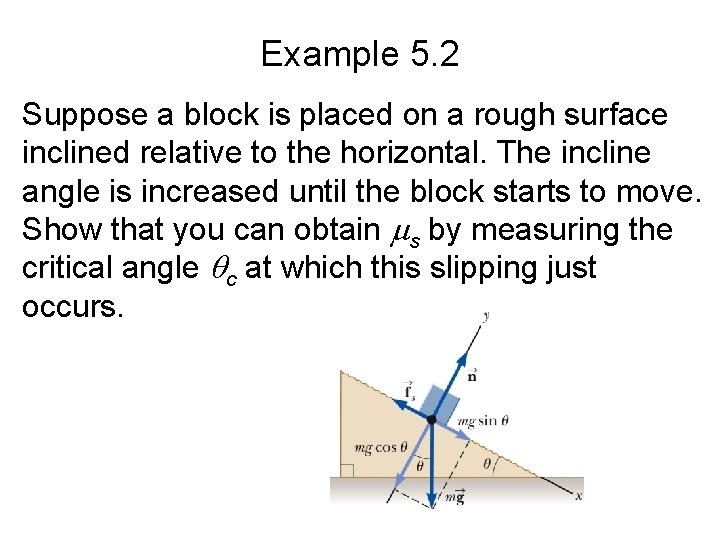
Example 5. 2 Suppose a block is placed on a rough surface inclined relative to the horizontal. The incline angle is increased until the block starts to move. Show that you can obtain s by measuring the critical angle c at which this slipping just occurs.

Example 5. 2 • Apply the particle in equilibrium model: • Substitute: • When the block is on the verge of slipping:

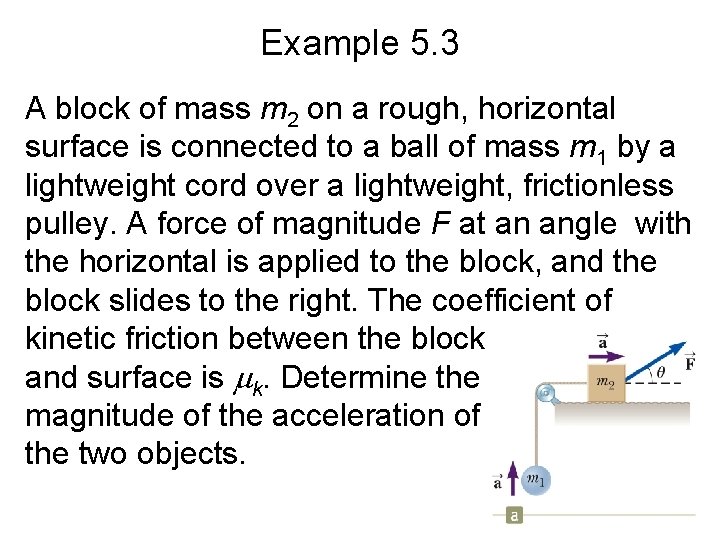
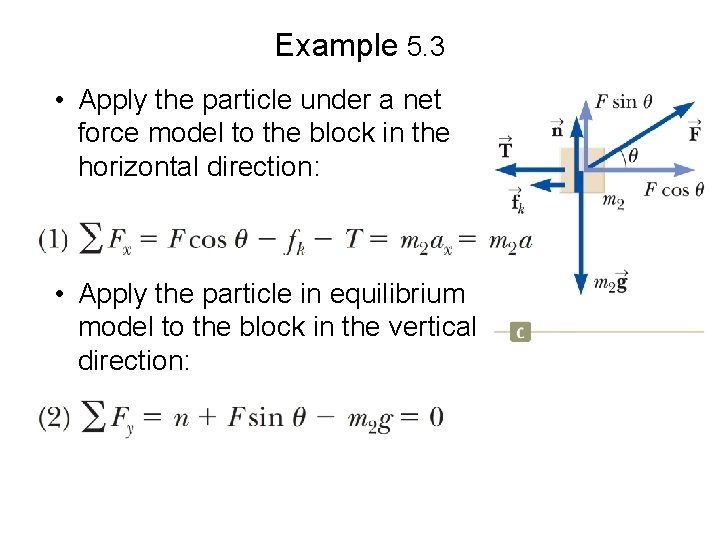
Example 5. 3 A block of mass m 2 on a rough, horizontal surface is connected to a ball of mass m 1 by a lightweight cord over a lightweight, frictionless pulley. A force of magnitude F at an angle with the horizontal is applied to the block, and the block slides to the right. The coefficient of kinetic friction between the block and surface is k. Determine the magnitude of the acceleration of the two objects.

Example 5. 3 • Apply the particle under a net force model to the block in the horizontal direction: • Apply the particle in equilibrium model to the block in the vertical direction:

Example 5. 3 – Apply the particle under a net force model to the ball in the vertical direction: – Solve Equation (2) for n:

Example 5. 3 – Substitute: – Solve for the acceleration:

Forces of Friction - 6 • Static Friction ØThe direction is opposite to the direction in which the object would move if there was no friction • Kinetic Friction ØThe direction is opposite to the direction in which the object is actually moving

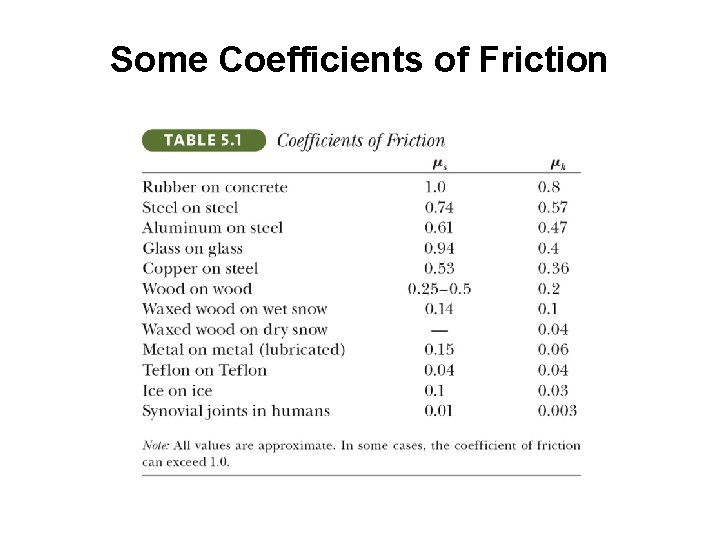
Some Coefficients of Friction

Friction Force Example - 1 • In moving a 35. 0 -kg desk from one side of a classroom to the other, a professor finds that a horizontal force of 275 N is necessary to set the desk in motion, and a force of 195 N is necessary to keep it in motion at a constant speed • What are the coefficients of (a) static and (b) kinetic friction between the desk and the floor? • (a) Ø Static friction Ø f s = m s. N Ø ms = fs/N = fs/mg = 275/(35)(9. 8) = 0. 802 • (b) Ø Kinetic friction Ø f k = m k. N Ø mk = fk/N = fk/mg = 195/(35)(9. 8) = 0. 569

Friction Force Example - 2 • • • An object has an initial velocity of 20 m/s Object slides on surface with mk = 0. 8 How far does the object slide until it stops? Ø Vertical • F = N – mg = ma = 0 • N = mg Ø Horizontal • Friction = -mk. N = -mkmg • F = -mkmg = ma • a = -mkg Ø Stopping distance • vf 2 = vi 2 + 2 ax • (we will soon learn this formula) • 0 = vi 2 – 2 mkgx • x = vi 2/2 mkg = 202/2/(. 8)/9. 8 • x = 25. 5 m

Friction Force Example - 3 • mk = 0. 4 • No friction Ø F = 400 = ma = 50 a Ø a = 8 m/s 2 • With friction Vertical Ø F = ma = 0 Ø -mg + N = 0 Ø N = mg = 50(9. 8) = 490 N Horizontal Ø fk = mk. N = 490(0. 4) = 196 N Ø F = P – fk = ma Ø 400 – 196 = 50 a Ø a = 204/50 = 4. 08 m/s 2

Friction Force Example - 4 • mk = 0. 4 • No friction Horizontal Ø Px = 400 cos 36. 9 = 320 Ø Py = 400 sin 36. 9 = 240 Ø F = Px = 320 = ma = 50 a Ø a = 320/50 = 6. 4 m/s 2 • With friction Vertical Ø F = -mg + N + Py = -490 + N + 240 = 0 Ø N = 490 – 240 = 250 Horizontal Ø fk = mk. N = 0. 4(250) = 100 Ø F = -fk + Px = -100 + 320 = ma = 50 a Ø a = 220/50 = 4. 4 m/s 2

Friction Force Example - 5 • mk = 0. 4 • No friction Horizontal Ø Px = 400 cos 36. 9 = 320 Ø Py = -400 sin 36. 9 = -240 Ø F = Px = 320 = ma = 50 a Ø a = 320/50 = 6. 4 m/s 2 • With friction Vertical v F = -mg + N + Py = -490 + N - 240 = 0 v N = 490 + 240 = 730 Horizontal Ø fk = mk. N = 0. 4(730) = 292 Ø F = -fk + Px = -292 + 320 = ma = 50 a Ø a = 28/50 = 0. 56 m/s 2

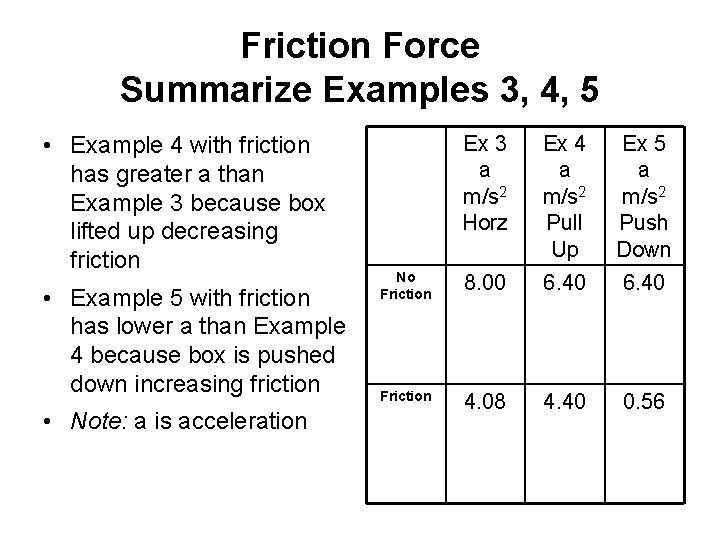
Friction Force Summarize Examples 3, 4, 5 • Example 4 with friction has greater a than Example 3 because box lifted up decreasing friction • Example 5 with friction has lower a than Example 4 because box is pushed down increasing friction • Note: a is acceleration Ex 3 a m/s 2 Horz Ex 4 a m/s 2 Pull Up Ex 5 a m/s 2 Push Down No Friction 8. 00 6. 40 Friction 4. 08 4. 40 0. 56

PHY 151: Lecture 5 More Applications of Newton’s Laws 5. 2 Particle in Uniform Motion

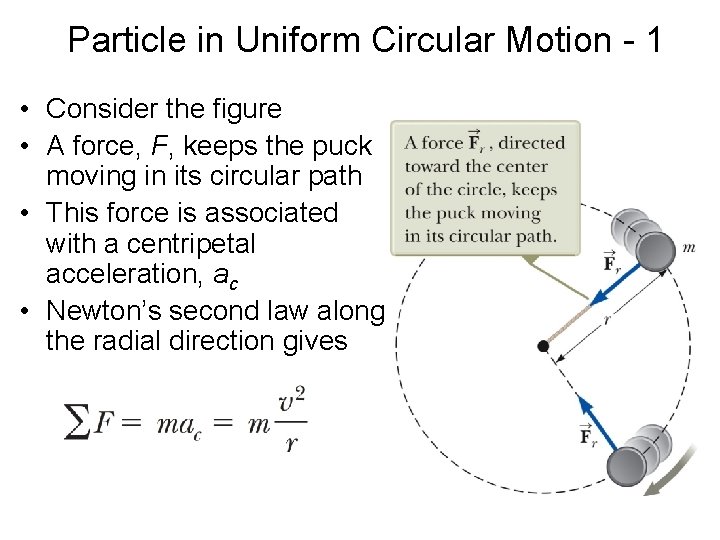
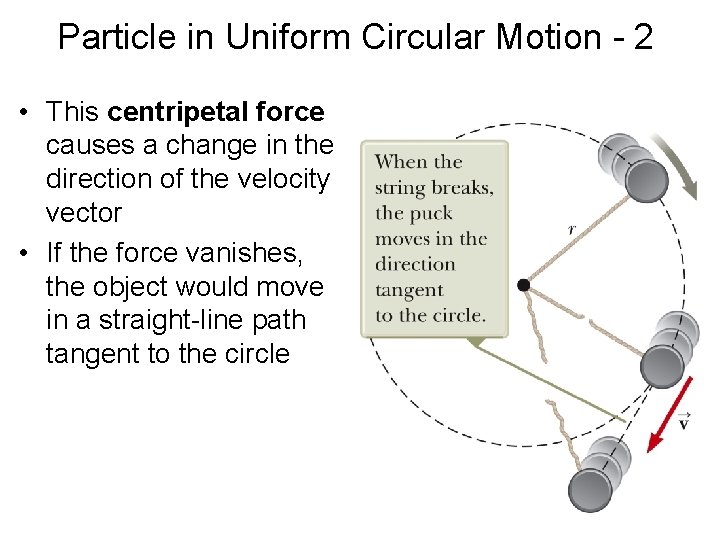
Particle in Uniform Circular Motion - 1 • Consider the figure • A force, F, keeps the puck moving in its circular path • This force is associated with a centripetal acceleration, ac • Newton’s second law along the radial direction gives

Particle in Uniform Circular Motion - 2 • This centripetal force causes a change in the direction of the velocity vector • If the force vanishes, the object would move in a straight-line path tangent to the circle

Example 5. 4 A puck of mass 0. 500 kg is attached to the end of a cord 1. 50 m long. The puck moves in a horizontal circle. If the cord can withstand a maximum tension of 50. 0 N, what is the maximum speed at which the puck can move before the cord breaks? Assume the string remains horizontal during the motion.

Example 5. 4 • Use Newton’s second law with tension: • Solve for v: • Find the maximum speed:

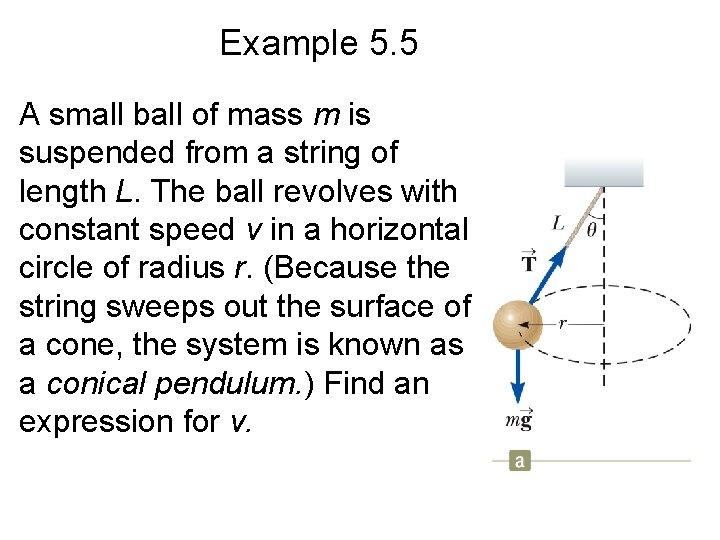
Example 5. 5 A small ball of mass m is suspended from a string of length L. The ball revolves with constant speed v in a horizontal circle of radius r. (Because the string sweeps out the surface of a cone, the system is known as a conical pendulum. ) Find an expression for v.

Example 5. 5 • Apply the particle in equilibrium model in the vertical direction: • Apply the particle in uniform circular motion model in the horizontal direction:
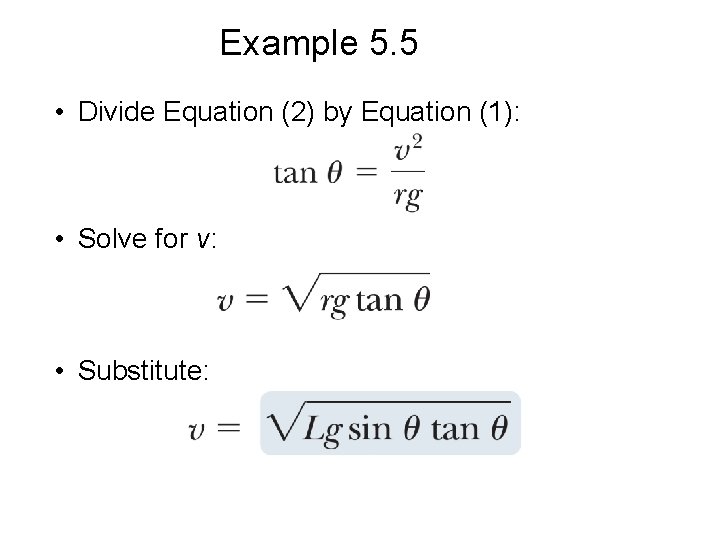
Example 5. 5 • Divide Equation (2) by Equation (1): • Solve for v: • Substitute:

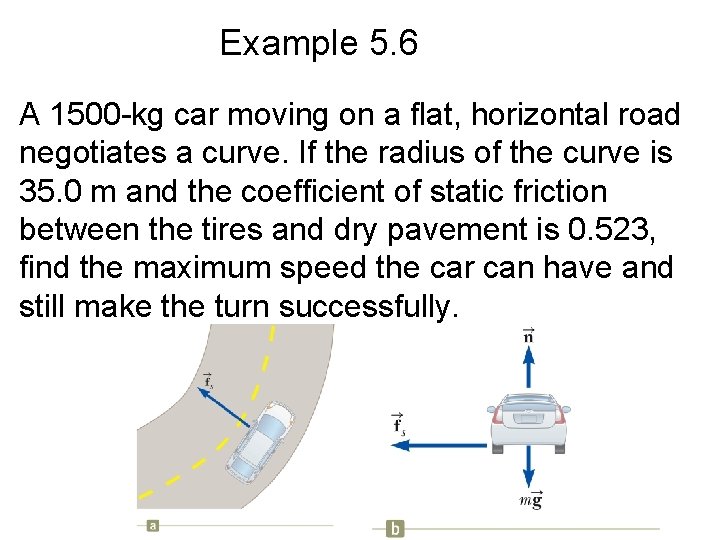
Example 5. 6 A 1500 -kg car moving on a flat, horizontal road negotiates a curve. If the radius of the curve is 35. 0 m and the coefficient of static friction between the tires and dry pavement is 0. 523, find the maximum speed the car can have and still make the turn successfully.

Example 5. 6 • Find the maximum speed condition: • Apply the particle in equilibrium model:

Example 5. 6 • Solve Equation (1) for speed: • Substitute numerical values:

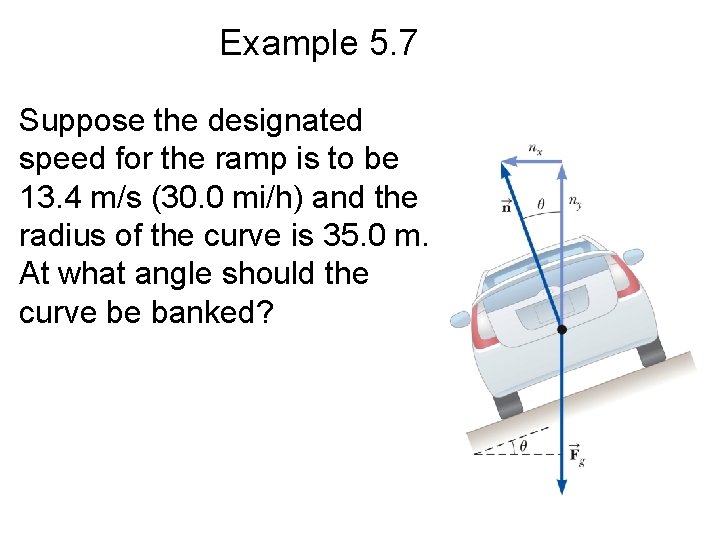
Example 5. 7 A civil engineer wishes to redesign the curved roadway in such a way that a car will not have to rely on friction to round the curve without skidding. In other words, a car moving at the designated speed can negotiate the curve even when the road is covered with ice. Such a road is usually banked, which means that the roadway is tilted toward the inside of the curve.

Example 5. 7 Suppose the designated speed for the ramp is to be 13. 4 m/s (30. 0 mi/h) and the radius of the curve is 35. 0 m. At what angle should the curve be banked?

Example 5. 7 – Write Newton’s second law in the radial direction: – Apply the particle in equilibrium model:

Example 5. 7 – Divide Equation (1) by Equation (2): – Solve for the angle:


Particle in Uniform Circular Motion - 3 • Very Important! • Take the positive direction for radial forces and accelerations be in the same direction as the centripetal acceleration • Depending on the nature of the problem, the positive direction can change

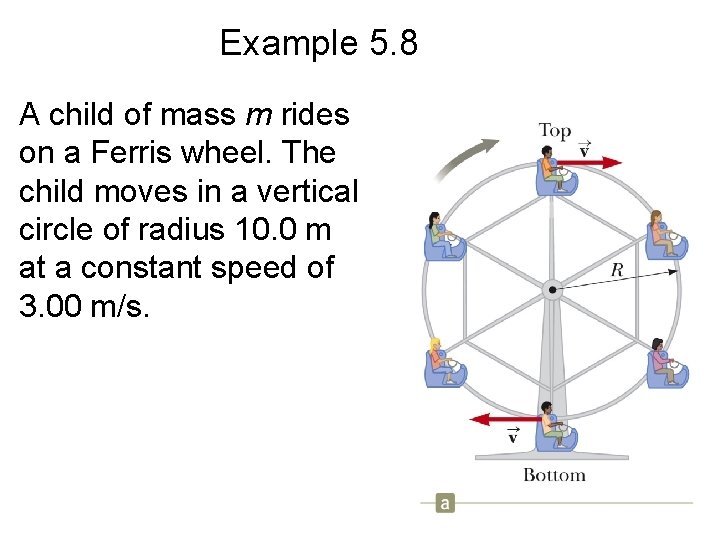
Example 5. 8 A child of mass m rides on a Ferris wheel. The child moves in a vertical circle of radius 10. 0 m at a constant speed of 3. 00 m/s.

Example 5. 8 (A) Determine the force exerted by the seat on the child at the bottom of the ride. Express your answer in terms of the weight of the child, mg. – Apply Newton’s second law in the radial direction:

Example 5. 8 • Solve for the force exerted by the seat on the child: • Substitute:

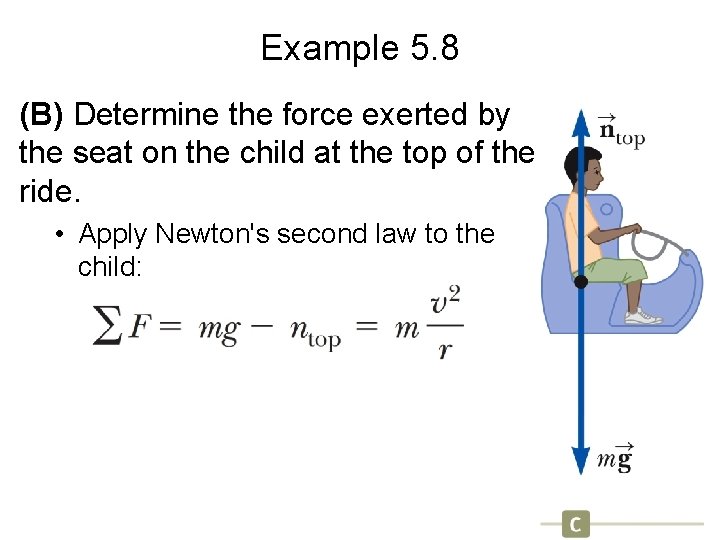
Example 5. 8 (B) Determine the force exerted by the seat on the child at the top of the ride. • Apply Newton's second law to the child:

Example 5. 8 • Solve for the force exerted by the seat on the child: • Substitute:

PHY 151: Lecture 5 More Applications of Newton’s Laws 5. 3 Nonuniform Circular Motion

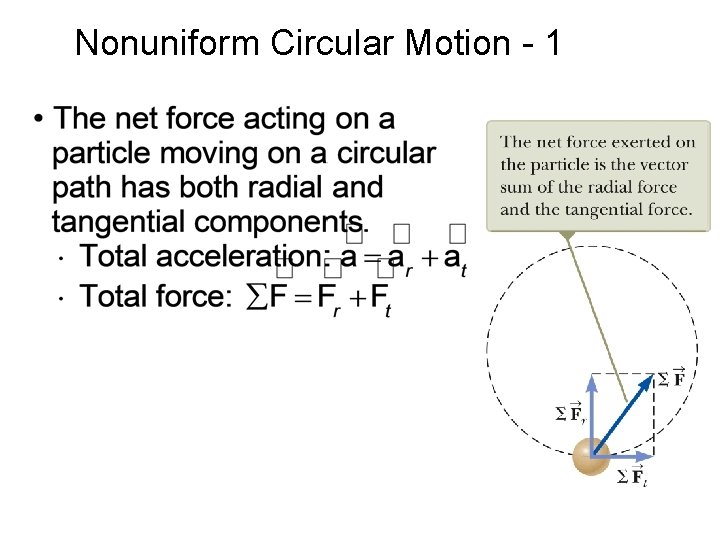
Nonuniform Circular Motion - 1

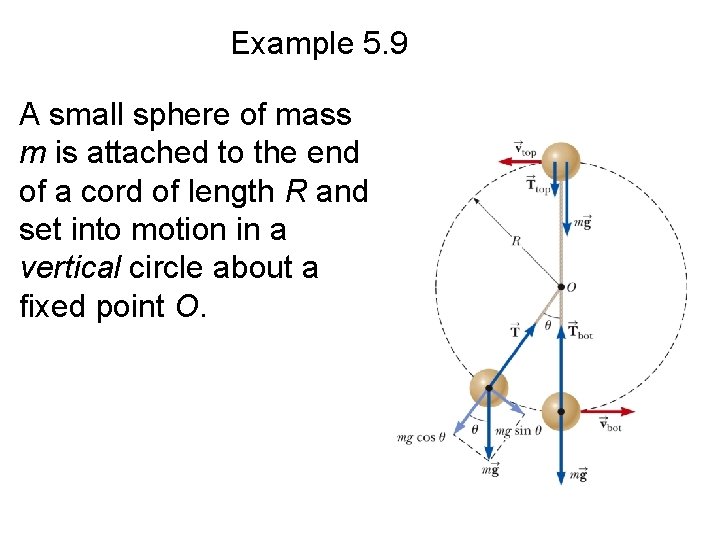
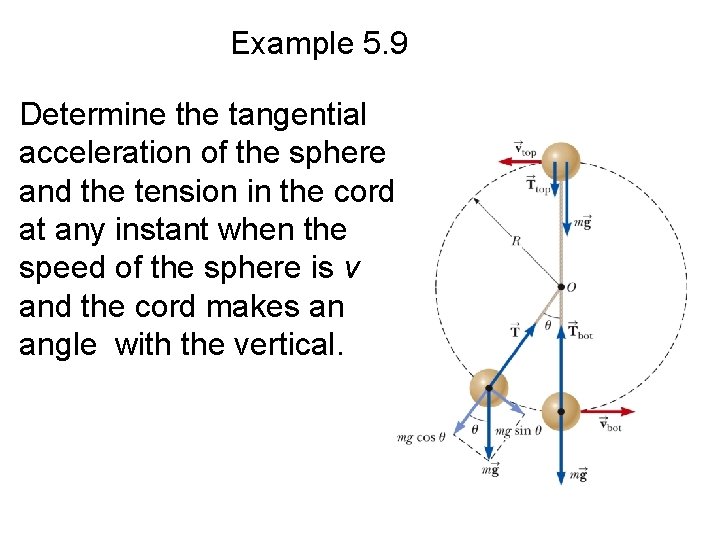
Example 5. 9 A small sphere of mass m is attached to the end of a cord of length R and set into motion in a vertical circle about a fixed point O.

Example 5. 9 Determine the tangential acceleration of the sphere and the tension in the cord at any instant when the speed of the sphere is v and the cord makes an angle with the vertical.

Example 5. 9 – Apply Newton’s second law to the sphere in the radial direction: – Apply Newton’s second law to the forces acting on the sphere in the radial direction:

PHY 151: Lecture 5 More Applications of Newton’s Laws 5. 4 Motion in the Presence of Velocity-Dependent Resistive Force

Motion in the Presence of Velocity. Dependent Resistive Forces - 1

Motion in the Presence of Velocity. Dependent Resistive Forces - 1 Model 1: Resistive Force Proportional to Object Velocity • At low speeds, the resistive force is proportional to the velocity:

Motion in the Presence of Velocity. Dependent Resistive Forces - 2 • Consider a small sphere falling through a liquid: • Looking at the vertical motion and choosing down as positive: • Dividing by mass: • This is called a differential equation

Motion in the Presence of Velocity. Dependent Resistive Forces - 3 • • Terminal speed can be calculated by setting a = dv/dt = 0: The expression which satisfies the differential equation is • • • v. T = mg/b = m/b (the time constant) e = 2. 718 29 (base of natural log)

Example 5. 10 A small sphere of mass 2. 00 g is released from rest in a large vessel filled with oil, where it experiences a resistive force proportional to its speed. The sphere reaches a terminal speed of 5. 00 cm/s. Determine the time constant and the time at which the sphere reaches 90. 0% of its terminal speed. • Evaluate the coefficient b:

Example 5. 10 • Evaluate the time constant : • Find the time when the sphere reaches 0. 900 v. T:

Motion in the Presence of Velocity. Dependent Resistive Forces - 4 Model 2: Resistive Force Proportional to Object Speed Squared • For objects moving at high speeds through air, the resistive force is approximately proportional to the square of the speed: • D is a dimensionless empirical quantity that is called the drag coefficient • r is the density of air • A is the cross-sectional area of the object • v is the speed of the object

Motion in the Presence of Velocity. Dependent Resistive Forces - 5 • Consider an object released from rest • The object experiences two forces, gravitational and resistive:

PHY 151: Lecture 5 More Applications of Newton’s Laws 5. 5 The Fundamental Forces of Nature

The Fundamental Forces of Nature - 1 Gravitational force: • Mutual force of attraction between any two objects in the Universe • Inherently the weakest of the fundamental forces • Described by Newton’s law of universal gravitation:

The Fundamental Forces of Nature - 2 Electromagnetic force: • Binds atoms and electrons in ordinary matter • Most of the forces we have discussed are ultimately electromagnetic in nature • Magnitude is given by Coulomb’s law:

The Fundamental Forces of Nature - 3 Strong force: • The force that binds the nucleons to form the nucleus of an atom • Attractive force • Extremely short range force • Negligible for r > ~10 14 m • For a typical nuclear separation, the nuclear force is about two orders of magnitude stronger than the electrostatic force

The Fundamental Forces of Nature - 4 Weak force: • Tends to produce instability in certain nuclei • Short-range force • About 1034 times stronger than gravitational force • About 103 times stronger than the electromagnetic force

The Fundamental Forces of Nature - 5 • Physicists have been searching for a simplification scheme that reduces the number of forces • Electromagnetic and weak forces are manifestations of the electroweak force • The nuclear force is now interpreted as a secondary effect of the strong force acting between quarks • Scientists believe that fundamental forces of nature are closely related to the origin of the Universe

PHY 151: Lecture 5 More Applications of Newton’s Laws 5. 6 Context Connection: Drag Coefficients of Automobiles Skipped

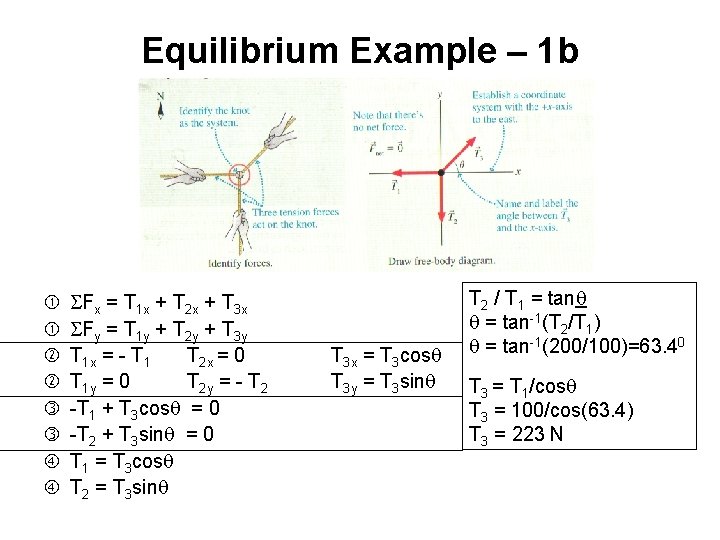
Equilibrium Example – 1 a • You and two friends find three ropes tied together with a single knot and decide to have a three-way tug-of-war • Alice pulls to the west with 100 N of force • Bob pulls to the south with 200 N • How hard, and in which direction, should you pull to keep the knot from moving?

Equilibrium Example – 1 b SFx = T 1 x + T 2 x + T 3 x SFy = T 1 y + T 2 y + T 3 y T 1 x = - T 1 T 2 x = 0 T 1 y = 0 T 2 y = - T 2 -T 1 + T 3 cosq = 0 -T 2 + T 3 sinq = 0 T 1 = T 3 cosq T 2 = T 3 sinq T 3 x = T 3 cosq T 3 y = T 3 sinq T 2 / T 1 = tanq q = tan-1(T 2/T 1) q = tan-1(200/100)=63. 40 T 3 = T 1/cosq T 3 = 100/cos(63. 4) T 3 = 223 N

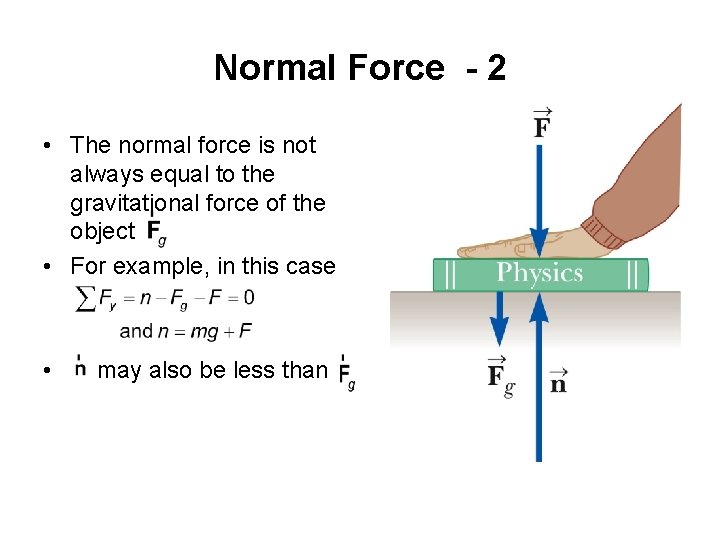
Normal Force - 1 • Normal force is one component of the force that a surface exerts on an object with which it is in contact • This is component that is perpendicular to the surface • Depending on the physical situation, the Normal Force can be vertical, horizontal, or some other direction • For example: – Block exerts a force on table by pressing down on it – Consistent with the third law, table exerts an oppositely directed force of equal magnitude on block – This reaction force is the normal force

Normal Force - 2 • The normal force is not always equal to the gravitational force of the object • For example, in this case • may also be less than

Normal Force Apparent Weight • There are situations in which a scale does not give correct weight • In such situations, the reading on the scale gives only the “apparent” weight, rather than the gravitational force or “true” weight • The apparent weight is the force that the object exerts on the scale with which it is in contact • Consider a person on a scale in an elevator: Ø If the elevator is not moving or moving with constant velocity, the scale registers the true weight Ø If the elevator is accelerating, apparent weight and the true weight are not equal Ø When the elevator accelerates upward, the apparent weight is greater than the true weight

Apparent Weight Example - 1 • Consider a person on a scale in an elevator • Normal force of scale on person is N in up direction • Weight of gravity, mg, on person is in down direction • Newton’s second law gives Ø F = N – mg = ma Ø N = ma + mg • “a” can be either + for up acceleration or – for down acceleration • N is the force the scale exerts on the person • By Newton’s third law, N is the force the person exerts on the scale, the apparent weight

Apparent Weight Example - 2 • A man of mass 80 kg stands in an elevator accelerating up at 4 m/s 2 • Calculate the Normal force on the man ØWeight down = -mg = -80(9. 8) = -784 N ØF = ma ØN – 784 = 80(4) ØN = 784 + 320 = 1004 N

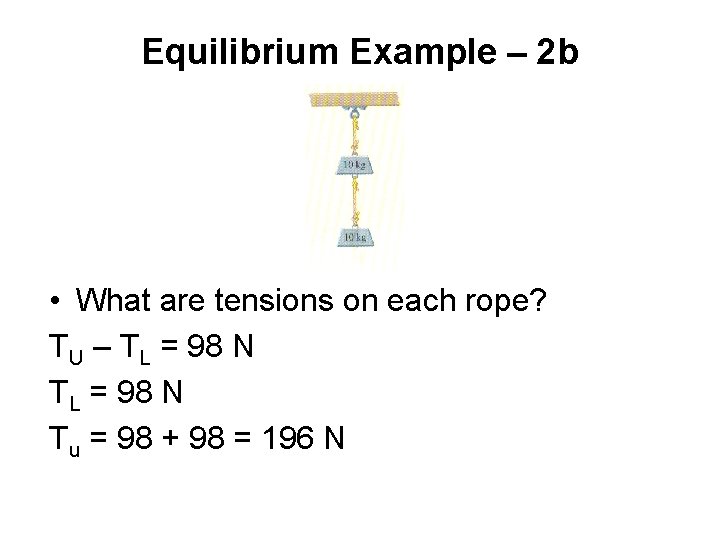
Equilibrium Example – 2 a • • What are tensions on each rope? Mass Upper: SFy = Wy + Ny + fy + Ty + Py=0 Wy=-(m. U)g=-(10)(9. 8)=-98 Ny = 0 fy = 0 Ty = TU-TL Py = 0 -98 + 0 + TU – TL + 0 = 0 TU – TL = 98 N Mass Lower: SFy = Wy + Ny + fy + Ty+Py=0 Wy=-m. Lg = -(10)(9. 8) = -98 Ny = 0 fy = 0 T y = T L Py = 0 -98+0+0+TL+0 =0 TL = 98 N

Equilibrium Example – 2 b • What are tensions on each rope? TU – TL = 98 N Tu = 98 + 98 = 196 N

Equilibrium Alternative Example – 2 c • • What are tensions on each rope? Mass Upper and Mass Lower: SFy = Wy + Ny + fy + Ty + Py=0 Wy=-(m. U+m. L)g=-(20)(9. 8)=-196 Ny = 0 fy = 0 Ty = T U Py = 0 -196 + 0 + TU + 0 = 0 TU = 196 N Mass Lower: SFy = Wy + Ny + fy + Ty+Py=0 Wy=-m. Lg = -(10)(9. 8) = -98 Ny = 0 fy = 0 T y = T L Py = 0 -98+0+0+TL+0 =0 TL = 98 N

Equilibrium Example – 3 a • A car with a weight of 15, 000 N is being towed up a 200 slope at constant velocity • Friction is negligible • The tow rope is rated at 6000 N maximum tension • Will it break?

Equilibrium Example – 3 b SFx = Wx + Nx + fx + Tx + Px SFy = Wy + Ny + fy + Ty + Py WX = -wsinq Wy = -wcosq Nx = 0 Ny= n Tx = T Ty = 0 T – Wsinq = 0 N – Wcosq = 0 T = (15000)sin(20) = 5130 N Rope will not break

Not in Equilibrium Example - 1 • • Two forces act on an object of mass 4. 00 kg One force is 40. 0 N in the +x-direction The other force is 60. 0 N in the + y-direction Find magnitude and direction of the acceleration of the object – x-direction Ø SFx = max Ø 40 = 4 ax Ø 40/4 = ax = 10 m/s 2 – y-direction Ø SFy = may Ø 60 = 4 ay Ø 60/4 = ay = 15 m/s 2 Ø magnitude of a = sqrt(102 + 152) = 18 m/s 2 Ø q = tan-1(15/10) = 560

Not in Equilibrium Example 2 • • • A boy pulls a box of mass 30 kg with a force of 25 N at an angle of 300 above the horizontal (a) Ignoring friction, what is the acceleration of the box? (b) What is the normal force exerted on the box by the ground? SFx = Wx + Nx + (fk)x + Tx + Px = max SFy = Wy + Ny + (fk)y + Ty + Py = may Wx = 0 Wy = mg = 30(-9. 8) = -294 Nx = 0 Ny = N Tx = 0 Ty = 0 (fk)x 0 (fk)y = 0 Px = 25 cos 30 = 21. 7 Py = 25 sin 30 = 12. 5 (a) x-direction 0 + 0 + 21. 7 = 30 ax ax = 21. 7/30 = 0. 72 m/s 2 (b) y-direction -294 + N +12. 5 = -281. 5 + N = 30 ay = 0 N = 281. 5 newtons

Multiple Objects • When two or more objects are connected or in contact, Newton’s laws may be applied to the system as a whole and/or to each individual object • Whichever you use to solve the problem, the other approach can be used as a check

Not in Equilibrium Example – 3 a • The Atwood machine consists of two masses suspended from a fixed pulley • m 1 = 0. 55 kg • m 2 = 0. 80 kg • (a) What is the acceleration of the system? • (b) What is magnitude of tension in string?

Not in Equilibrium Example - 3 b • (a) – Mass 1: SFy = Wy + Ny + (fk)y + Ty + Py = may Wy = -m 1 g Ny = 0 Ty = T (fk)y = 0 Py = 0 -0. 55 g +0 + T + 0 = 0. 55 ay – Mass 2: Wy = -m 2 g Ny = 0 Ty = T (fk)y = 0 Py = 0 -0. 80 g +0 + T + 0 = -0. 80 ay Subtract equations: 0. 25 g = 1. 35 ay ay = 1. 8 m/s 2

Not in Equilibrium Example 3 c • (b) -0. 55 g + T = 0. 55 ay + 0. 55 g T = 0. 55(1. 8) + 0. 55(9. 8) = 6. 4 N

Not in Equilibrium Alternative Example - 3 d • The Atwood machine consists of two masses suspended from a fixed pulley • m 1 = 0. 55 kg • m 2 = 0. 80 kg • (a) What is the acceleration of the system? • (b) What is magnitude of tension in string?

Not in Equilibrium Alternative Example – 3 e a m 1 Pull = m 2 g Pull = m 1 g • • • Lift masses m 1 and m 2 so that they are horizontal Gravity on m 1 becomes a pull to the left Gravity on m 2 becomes a pull to the right Treat two masses and rope between as a single system Tension in the rope is an Internal force and is ignored in Newton’s Second Law

Not in Equilibrium Alternative Example – 3 f • Mass 1 + Mass 2: SFx = Wx + Nx + (fk)x + Tx + Px = max Wx = 0 Nx = 0 Tx = 0 (fk)x = 0 Px = -m 1 g + m 2 g -0. 55 g+0. 80 g + 0 + 0 = (0. 55 + 0. 8)ax ax =. 25(9. 8) / 1. 35 = 1. 8 m/s 2 Mass 1: Wx = -m 1 g Nx = 0 Tx = T (fk)x = 0 Px = 0 -0. 55 g +0 + T + 0 = 0. 55(1. 8) T = 0. 99 + 0. 55(9. 8) = 6. 4 N

Not in Equilibrium Example – 4 a • Three blocks are pulled along a frictionless surface by a horizontal force of F = 18. 0 N • (a) What is the acceleration of the system? • (b) What are tension forces in the strings?

Not in Equilibrium – Example 4 b • Mass 1: SFx = Wx+Nx+(fk)x+Tx+Px =m 1 ax Wx = 0 Nx = 0 Tx = T 1 (fk)x = 0 Px = 0 0 + 0 + T 1 + 0 = m 1 ax T 1 = 1. 0 ax (Equation 1) Mass 2: SFx=Wx+Nx+(fk)x+Tx+Px=m 2 ax W x = 0 Nx = 0 Tx = -T 1+T 2 (fk)x = 0 P x = 0 0 + 0 - T 1 + T 2 + 0 = m 2 ax -T 1 + T 2 = m 2 ax -T 1 + T 2 = 2. 0 ax (Equation 2)

Not in Equilibrium Example – 4 c • Mass 3: SFx = Wx Nx+(fk)x+Tx+Px =m 3 ax Wx = 0 Nx = 0 Tx = -T 2 (fk)x = 0 Px = P 0 + 0 - T 2 + P = m 3 ax -T 2 + P = m 3 ax -T 2 + 18. 0 = 3. 0 ax (Equation 3) Add Equations 1 and 2 T 2 = 3. 0 ax (Equation 4) Add Equations 3 and 4 18. 0 = 6. 0 ax ax = 18. 0/6. 0 = 3. 0 m/s 2 Substitute into Equation 1 T 1 = 1. 0(3. 0) = 3. 0 N Substitute into Equation 3 T 2 = 18. 0 – 3. 0(3. 0) = 9. 0 N

Not in Equilibrium Alternative Example – 4 d • Mass 1, Mass 2, and Mass 3: Mass 1: SFx = Wx+Nx+(fk)x+Tx+Px =max Wx = 0 Nx = 0 Tx = 0 (fk)x = 0 Px = P 0+0+P = (m 1+m 2+m 3)ax 18. 0 = 6. 0 ax ax=18. 0 / 6. 0=3. 0 (Equation 1) SFx=Wx+Nx+(fk)x+Tx+Px=m 1 ax W x = 0 Nx = 0 T x = T 1 (fk)x = 0 P x = 0 0 + 0 + T 1 + 0 = m 1 ax T 1 = (1. 0)(3. 0) = 3. 0 N

Not in Equilibrium Alternative Example – 4 e • Mass 3: SFx = Wx + Nx + (fk)x + Tx + Px =m 3 ax Wx = 0 Nx = 0 Tx = -T 2 (fk)x = 0 Px = P 0 + 0 – T 2 + P = m 3 ax T 2 = P – m 3 ax T 2 = 18 – (3. 0) = 9. 0 N

Not in Equilibrium Example - 5 a • Pulleys are frictionless • There is no friction between mass m 3 and the table • What is the acceleration of the system? • m 1=0. 25 kg, m 2 = 0. 50 kg, m 3 = 0. 25 kg

Not in Equilibrium Example 5 b • Mass 1: SF =Wy+Ny+(fk)y+Ty+Py=m 1 a Wy = -m 1 g Ny = 0 Ty = T 1 (fk)y = 0 Py = 0 -m 1 g + 0 + T 1 + 0 = m 1 a -m 1 g+T 1=m 1 a (Equation 1) Mass 2: SF =Wy+Ny+(fk)y+Ty+Py=m 2 a Wy = -m 2 g Ny = 0 T y = T 2 (fk)y = 0 P y = 0 -m 2 g + 0 + T 2 + 0 = m 2(-a) -m 2 g+ T 2=-m 2 a (Equation 2)

Not in Equilibrium Example 5 c • Mass 3: SFx=Wx+Nx+(fk)x+Tx+Px=ma Wx = 0 Nx = 0 Tx = -T 1 + T 2 (fk)x = 0 Px = 0 0 + 0 – T 1 + T 2 + 0 = m 3 a – T 1+T 2=m 3 a (Equation 3) Subtract equation 2 from equation 1 (m 2 -m 1)g-T 2+T 1=(m 1+m 2)a (Eq. 4) Add equations 3 and 4 (m 2 -m 1)g=(m 1+m 2+m 3)a a = (m 2 -m 1)g/(m 1+m 2+m 3) a = (0. 50 -0. 25)(9. 8)/(0. 50+0. 25+0. 5) a = 2. 45 m/s 2

Not in Equilibrium Alternative Example – 5 d • Mass 1, Mass 2, and Mass 3 SFx=Wx+Nx+(fk)x+Tx+Px=ma Wx = 0 Nx = 0 Tx = 0 (fk)x = 0 Px = -m 1 g+m 2 g 0+0+0+0 -m 1 g+m 2 g = ma -m 1 g+m 2 g=ma a = g(m 2 -m 1)/(m 1+m 2+m 3) a=(9. 8)(0. 50 -0. 25)/1=2. 45 m/s 2 Mass 1: SF =Wy+Ny+(fk)y+Ty+Py=m 2 a W y = 0 Ny = 0 T y = T 1 (fk)y = 0 Py = -m 1 g 0 + 0 + T 1 – m 1 g = m 1 a -m 1 g+ T 1=m 1 a+m 1 g = (0. 25)(9. 8+2. 45) T 1 = 3. 1 N

Not in Equilibrium Alternative Example – 5 e Mass 3: SF =Wy+Ny+(fk)y+Ty+Py=m 2 a W y = 0 Ny = 0 T y = T 2 (fk)y = 0 Py = -m 3 g 0 + 0 + T 2 – m 3 g = -m 3 a -m 3 g+ T 2=-m 3 a+m 3 g = (0. 25)(9. 8 -2. 45) T 2 = 1. 8 N

Not in Equilibrium Alternative Example – 6 a • Weight of the block on table is 422 N • Weigh of the hanging block is 185 N • Ignoring all friction and assume the pulley is massless • (a) Find the acceleration of the two blocks • (b) Find the tension in the cord – Mass of table block is m 1 = 422/9. 8 =43. 06 kg – Mass of hanging block is m 2 = 185/9. 8 = 18. 88 kg

Not in Equilibrium Alternative Example 6 b • Mass 1 and Mass 2: Mass 1: SFx=Wx+Nx+(fk)x+Tx+Px=ma Wx = 0 Nx = 0 Tx = 0 (fk)x = 0 Px = m 2 g 0+0+m 2 g = (m 1 + m 2)a a = -g(m 2/(m 1+m 2) a=(9. 8)(18. 88)/(61. 94)=2. 99 m/s 2 SFx=Wx+Nx+(fk)x+Tx+Px=m 1 a W x = 0 Nx = 0 T x = T (fk)x = 0 P x = 0 0+0+0+T+0 = m 1 a T = m 1 a T = 43. 06(2. 99) = 128. 8 N
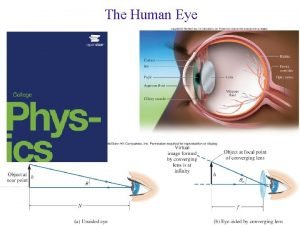
 What is farsightedness called
What is farsightedness called 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Phy-105 5 discussion
Phy-105 5 discussion Phy 205
Phy 205 General physics 1 measurements
General physics 1 measurements Phy 110
Phy 110 Phy 231 msu
Phy 231 msu Phy
Phy Phy
Phy Phy 108
Phy 108 Rikard blunck
Rikard blunck Phy 113 past questions and answers
Phy 113 past questions and answers Real image
Real image Vx=vox+axt
Vx=vox+axt Eye phy
Eye phy The great orthogonality theorem
The great orthogonality theorem Complete motion diagram
Complete motion diagram Atm packet phy
Atm packet phy Phy tgen
Phy tgen Phy 1214
Phy 1214 Phy 121 asu
Phy 121 asu Phy 2048c fsu
Phy 2048c fsu Phy 1214
Phy 1214 Phy 2049
Phy 2049 Phy 132
Phy 132 Rotational statics
Rotational statics Felix connects a wire coil to an ammeter
Felix connects a wire coil to an ammeter Phy
Phy 2012 phy
2012 phy Ddr phy architecture
Ddr phy architecture Physics heat and temperature
Physics heat and temperature Phy
Phy Phy 131 past papers
Phy 131 past papers Physics 2
Physics 2 Phy 1214
Phy 1214 Phy theorem
Phy theorem Life phy
Life phy Phy 2049
Phy 2049 1,151,725 bytes
1,151,725 bytes Chemistry 151 final exam
Chemistry 151 final exam Dpr 151/2011
Dpr 151/2011 Software consists of:
Software consists of: Tổng kết vốn từ 151
Tổng kết vốn từ 151 151 food
151 food Model netics
Model netics Econ 151
Econ 151 Item 151
Item 151 118/151
118/151 Mcb 317 uiuc
Mcb 317 uiuc Hino 151
Hino 151 Sjsu cs 151
Sjsu cs 151 Apsc 143 queens
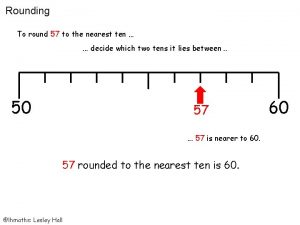
Apsc 143 queens 71 to the nearest 10
71 to the nearest 10 Econ 151
Econ 151 Econ 151
Econ 151 Cs 133 uci
Cs 133 uci Cs 151 sjsu
Cs 151 sjsu Balanced forces and unbalanced forces venn diagram
Balanced forces and unbalanced forces venn diagram Example for unlike parallel forces
Example for unlike parallel forces δ+
δ+ What is constructive force
What is constructive force The forces shown above are
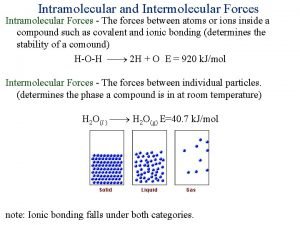
The forces shown above are Intermolecular force of attraction
Intermolecular force of attraction Contact force
Contact force Intramolecular forces vs intermolecular forces
Intramolecular forces vs intermolecular forces Instruction de lecture
Instruction de lecture Waves physics pdf notes
Waves physics pdf notes English literature lecture
English literature lecture Divine principle 3 hour lecture
Divine principle 3 hour lecture Machine learning lecture notes
Machine learning lecture notes Phy101 lecture 2
Phy101 lecture 2 Osi model lecture
Osi model lecture Application of mechatronics ppt
Application of mechatronics ppt Ideal diode formula
Ideal diode formula Performance management lecture
Performance management lecture Nutritive value of watermelon
Nutritive value of watermelon Aims of health psychology
Aims of health psychology Trois femmes puissantes lecture cursive
Trois femmes puissantes lecture cursive Project management lecture
Project management lecture Petit pays chapitre
Petit pays chapitre Electricity and magnetism lecture notes
Electricity and magnetism lecture notes Transformer lecture
Transformer lecture Sociology lecture
Sociology lecture Flow cytometry lecture
Flow cytometry lecture Project quality management lecture notes
Project quality management lecture notes Tiu lecture notes medical analysis
Tiu lecture notes medical analysis In this lecture
In this lecture Anderson localization lecture notes
Anderson localization lecture notes Atmospheric physics lecture notes
Atmospheric physics lecture notes Lecture handout
Lecture handout Randy pausch last lecture summary
Randy pausch last lecture summary Lesson collocation
Lesson collocation Introduction of chromatography
Introduction of chromatography Dsp lecture
Dsp lecture Bayesian decision theory lecture notes
Bayesian decision theory lecture notes Minecraft hardness
Minecraft hardness Things fall apart traditions and customs
Things fall apart traditions and customs Molecular biology of the cell
Molecular biology of the cell Management fifteenth edition
Management fifteenth edition Texte lecture pas à pas
Texte lecture pas à pas Lecture collocations
Lecture collocations L'histoire du friauche le dernier jour d'un condamné
L'histoire du friauche le dernier jour d'un condamné