PHY 151 Lecture 4 A 4 1 Position

PHY 151: Lecture 4 A • 4. 1 Position, Velocity, and Acceleration Vectors • 4. 2 Two-Dimensional Motion with Constant Acceleration • 4. 3 Projectile Motion

PHY 151: Lecture 4 A Motion in Two Dimensions 4. 1 Position, Velocity, and Acceleration Vectors

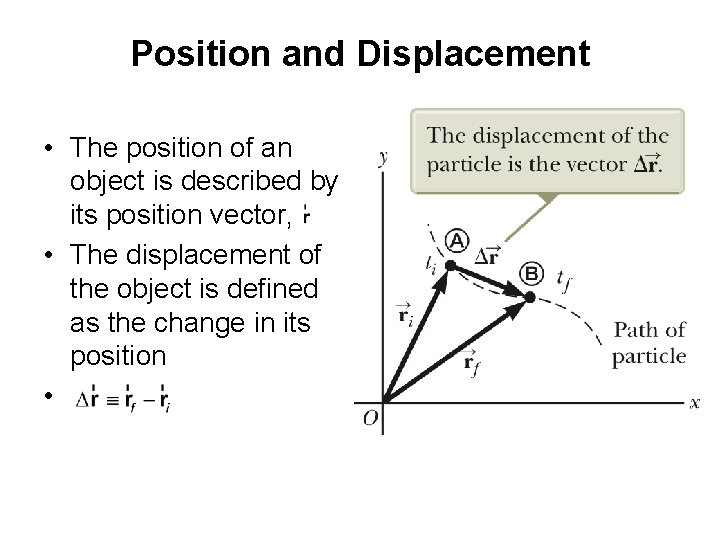
Position and Displacement • The position of an object is described by its position vector, • The displacement of the object is defined as the change in its position •

General Motion Ideas • In two- or three-dimensional kinematics, everything is the same as in onedimensional motion except that we must now use full vector notation – Positive and negative signs are no longer sufficient to determine the direction

Average Velocity • The average velocity is the ratio of the displacement to the time interval for the displacement • The direction of the average velocity is the direction of the displacement vector • The average velocity between points is independent of the path taken – This is because it is dependent on the displacement, which is also independent of the path

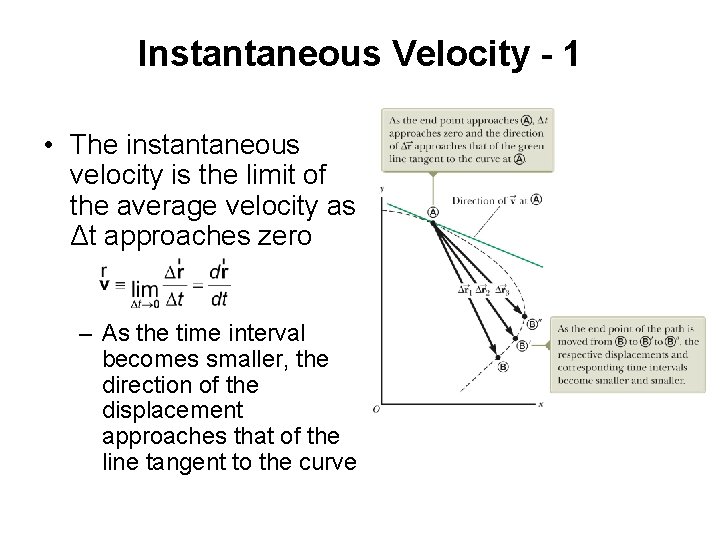
Instantaneous Velocity - 1 • The instantaneous velocity is the limit of the average velocity as Δt approaches zero – As the time interval becomes smaller, the direction of the displacement approaches that of the line tangent to the curve

Instantaneous Velocity - 2 • The direction of the instantaneous velocity vector at any point in a particle’s path is along a line tangent to the path at that point and in the direction of motion • The magnitude of the instantaneous velocity vector is the speed – The speed is a scalar quantity

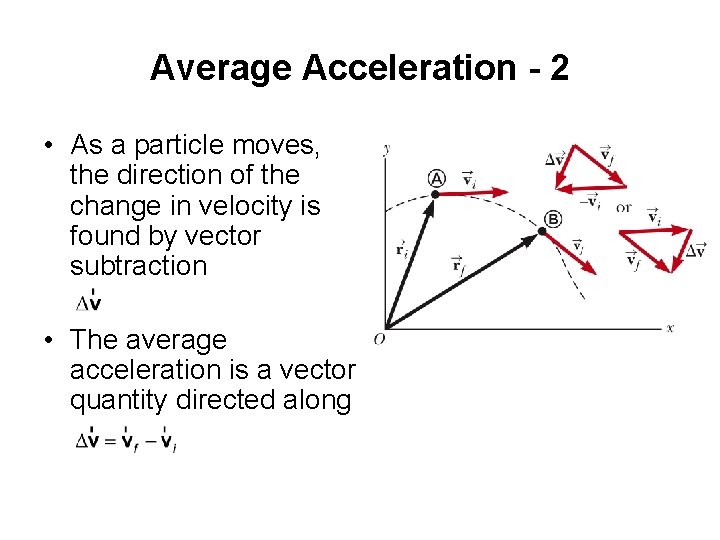
Average Acceleration - 1 • The average acceleration of a particle as it moves is defined as the change in the instantaneous velocity vector divided by the time interval during which that change occurs

Average Acceleration - 2 • As a particle moves, the direction of the change in velocity is found by vector subtraction • The average acceleration is a vector quantity directed along

Instantaneous Acceleration • The instantaneous acceleration is the limiting value of the ratio as Δt approaches zero – The instantaneous equals the derivative of the velocity vector with respect to time

Producing An Acceleration • Various changes in a particle’s motion may produce an acceleration – The magnitude of the velocity vector may change – The direction of the velocity vector may change • Even if the magnitude remains constant – Both may change simultaneously

PHY 151: Lecture 4 A Motion in Two Dimensions 4. 2 Two-Dimensional Motion with Constant Acceleration

Kinematic Equations for Two-Dimensional Motion • When the two-dimensional motion has a constant acceleration, a series of equations can be developed that describe the motion • These equations will be similar to those of onedimensional kinematics • Motion in two dimensions can be modeled as two independent motions in each of the two perpendicular directions associated with the x and y axes – Any influence in the y direction does not affect the motion in the x direction

Kinematic Equations - 2 • Position vector for a particle moving in the xy plane • The velocity vector can be found from the position vector – Since acceleration is constant, we can also find an expression for the velocity as a function of time:

Kinematic Equations 3 • The position vector can also be expressed as a function of time: – – This indicates that the position vector is the sum of three other vectors: • The initial position vector • The displacement resulting from the initial velocity • The displacement resulting from the acceleration

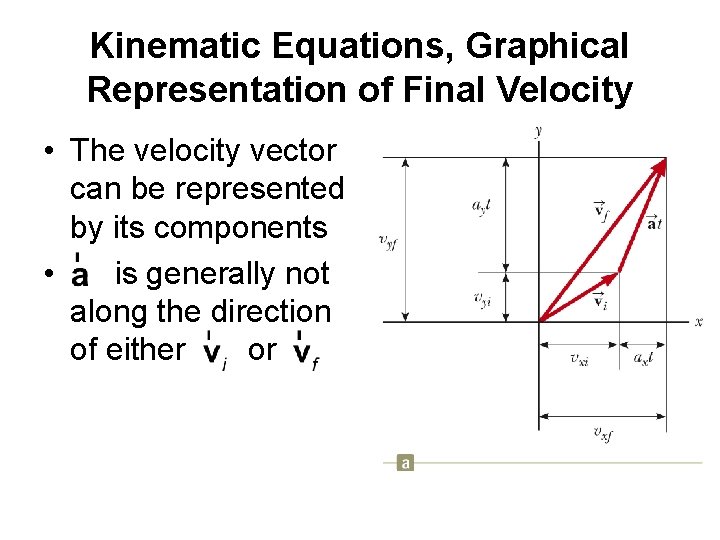
Kinematic Equations, Graphical Representation of Final Velocity • The velocity vector can be represented by its components • is generally not along the direction of either or

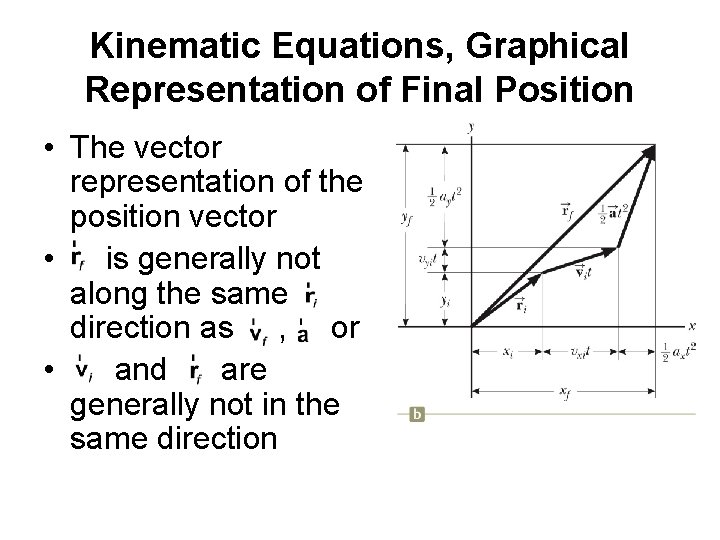
Kinematic Equations, Graphical Representation of Final Position • The vector representation of the position vector • is generally not along the same direction as , or • and are generally not in the same direction

PHY 151: Lecture 4 A Motion in Two Dimensions 4. 3 Projectile Motion

Projectile Motion - 1 • An object may move in both the x and y directions simultaneously • The form of two-dimensional motion we will deal with is called projectile motion

Assumptions of Projectile Motion • Horizontal § vxf = vxi § ax = 0 m/s 2 • Vertical § § § ay = -9. 8 m/s 2 g = acceleration of gravity = 9. 8 m/s 2 g is positive Use g as ay = –g No air resistance

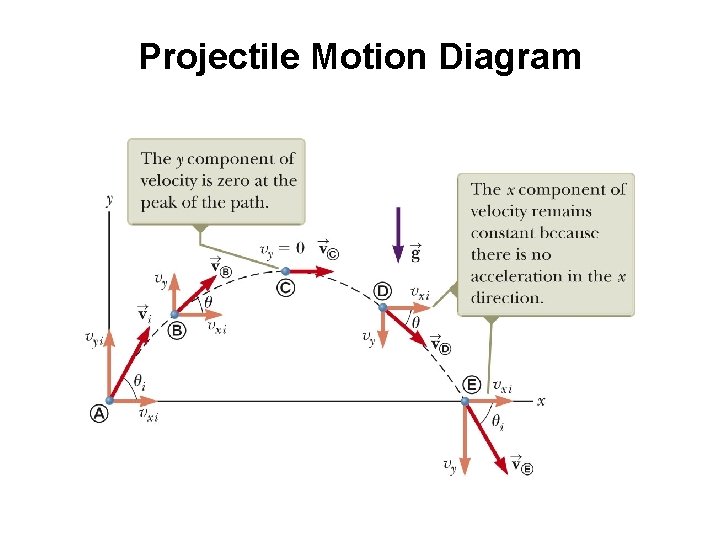
Projectile Motion Diagram

Acceleration at the Highest Point • The vertical velocity is zero at the top • The acceleration is not zero anywhere along the trajectory – If the projectile experienced zero acceleration at the highest point, its velocity at the point would not change • The projectile would move with a constant horizontal velocity from that point on

Analyzing Projectile Motion • Consider the motion as the superposition of the motions in the x- and y-directions • The actual position at any time is given by: • The initial velocity can be expressed in terms of its components. – vxi = vi cos q and vyi = vi sin q • The x-direction has constant velocity – ax = 0 • The y-direction is free fall – ay = -g

Projectile Motion Vectors • • The final position is the vector sum of the initial position, the position resulting from the initial velocity and the position resulting from the acceleration

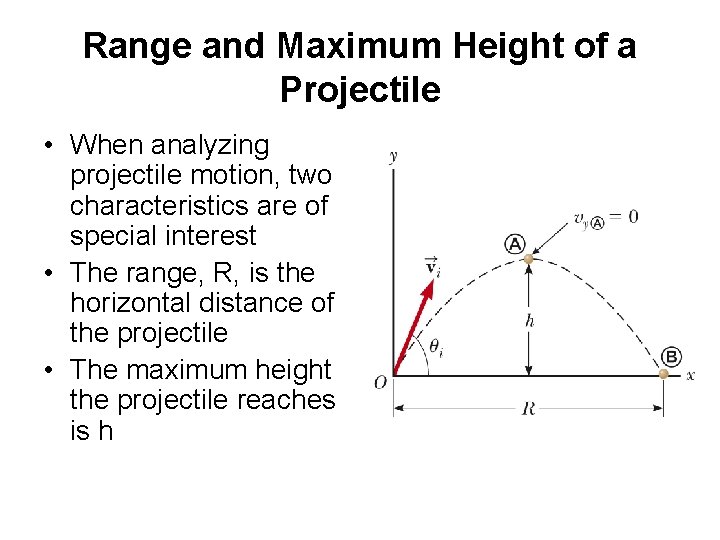
Range and Maximum Height of a Projectile • When analyzing projectile motion, two characteristics are of special interest • The range, R, is the horizontal distance of the projectile • The maximum height the projectile reaches is h

Height of a Projectile, equation • The maximum height of the projectile can be found in terms of the initial velocity vector: • This equation is valid only for symmetric motion

Description of Range • • • Object is fired at angle q to horizontal Object is fired at a height 0 Object returns to the height 0 This is a symmetric trajectory Trajectory is a parabola Horizontal distance from starting to final position is the Range

Range Formula • y-motion gives time-of-flight § § y = visinqt – (1/2)gt 2 0 = visinq – (1/2)gt t =2 visinq/g • x-motion give Range, R § § x = R= (vicosq)t R = (vicosq)(2 visinq/g) R=(vi 2/g)2 sinqcosq R=(vi 2/g)sin 2 q

Range Formula – Example 1 • An M 16 bullet has an initial velocity of 950 m/s • The bullet is fired at an angle of 450 • What is it’s maximum range? ØR=(vi 2/g)sin 2 q ØR=(9502/9. 8)sin(2 x 45) = 92. 1 km

Range Formula – Example 2 • A motorcycle travelling at 50 m/s wants to jump a gap to 200 m • At what angle should the motorcycle be launched? ØR=(vi 2/g)sin(2 q) Ø 200=(2500/9. 8)sin(2 q) Øsin(2 q) = 200(9. 8)/2500 = 0. 785 Øq = 25. 860 and 64. 140

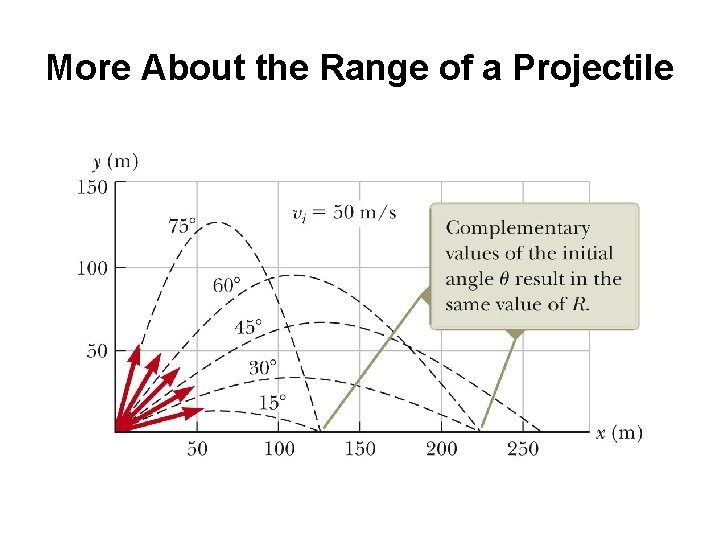
More About the Range of a Projectile

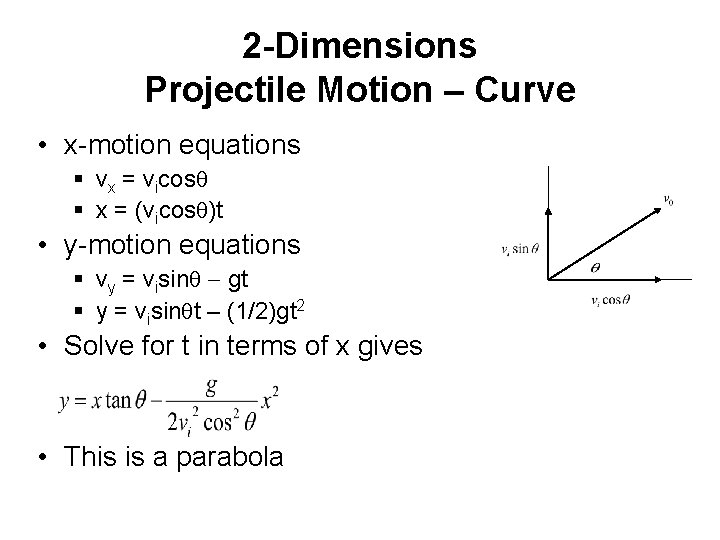
2 -Dimensions Projectile Motion – Curve • x-motion equations § vx = vicosq § x = (vicosq)t • y-motion equations § vy = visinq - gt § y = visinqt – (1/2)gt 2 • Solve for t in terms of x gives • This is a parabola

Angle for Maximum Range • Maximum range when sin(2 q) = 1 • 2 q = 900 • q = 450

Range of a Projectile, final • The maximum range occurs at qi = 45 o • Complementary angles will produce the same range – The maximum height will be different for the two angles – The times of the flight will be different for the two angles

Projectile Motion – Problem Solving Hints • Categorize – Confirm air resistance is neglected – Select a coordinate system with x in the horizontal and y in the vertical direction • Analyze – If the initial velocity is given, resolve it into x and y components – Treat the horizontal and vertical motions independently – Analyze the horizontal motion with the particle-underconstant-velocity model – Analyze the vertical motion with the particle-underconstant-acceleration model – Remember that both directions share the same time

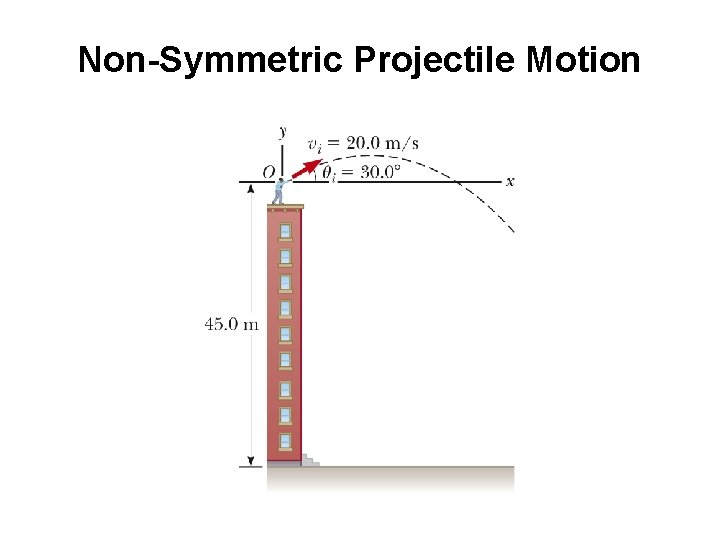
Non-Symmetric Projectile Motion

Projectile Motion – Example 1 a • • Ball with horizontal speed of 1. 5 m/s rolls off bench 2. 0 m high (a) How long will it take the ball to reach floor? Ø Horizontal xf = xi + vt xi = 0 xf = ? v = 1. 5 t=? xf = 0 + 1. 5 t Equation has xf, t Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 2 yf = 0 vi = 0 vf = ? a = -9. 8 t = ? vf = 0 – 9. 8 t Equation has vf, t 0 = 2 + 0 t + ½(-9. 8)t 2 Equation has t 02 = 402+2(-9. 8)(yf– 100) Equation has yf 0 = 2 + 0 t + ½(-9. 8)t 2 t = sqrt(-4/-9. 8) = 0. 64 s

2 -Dimensions Projectile Motion – Example 1 b • Ball with horizontal speed of 1. 5 m/s rolls off bench 2. 0 m high • How far from point on floor directly below edge of the bench will ball land? Ø Horizontal xf = xi + vt xi = 0 xf = ? v = 1. 5 t = 0. 64 xf = 0 + 1. 5(0. 64) Equation has xf = 0 + 1. 5(0. 64) = 0. 96 m

2 -Dimensions Projectile Motion – Example 2 (Find Time) • Ball rolls horizontally with speed of 7. 6 m/s off edge of tall platform • Ball lands 8. 7 m from the point on ground directly below edge of platform • What is height of platform? Ø Horizontal xf = xi + vt xi = 0 xf = 8. 7 v = 7. 6 t = ? 8. 7 = 0 + 7. 6 t t = 8. 7 / 7. 6 = 1. 14 s Equation has t

Projectile Motion – Example 2 (Find Height) • Ball rolls horizontally with speed of 7. 6 m/s off edge of tall platform • Ball lands 8. 7 m from point on ground directly below platform • What is height of platform? Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = ? yf = 0 vi = 0 vf = ? a = -9. 8 t = 1. 14 vf = 0 – 9. 8(1. 14) Equation has vf 0 = yi + 0(1. 14) + ½(-9. 8)(1. 14)2 Equation has yi vf 2 = 02+2(-9. 8)(yf–yi) Equation has yi, yf, vf 0 = yi + 0(1. 14) + ½(-9. 8)(1. 14)2 yi =-(1/2)(-9. 8)(1. 14)2 = 6. 37 m

Projectile Motion – Example 3 a • • A rifle fires a bullet at a speed of 250 m/s at an angle of 370 above the horizontal. (a) What height does the bullet reach? Ø Horizontal Ø xf = xi + vt xi = 0 v=250 cos(37)=199. 7 xf = 0 + 199. 7 t Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 vi = 250 sin(37)=150. 5 a = -9. 8 0 = 150. 5 – 9. 8 t yf = 0 + 150. 5 t + ½(-9. 8)t 2 02 = 150. 52+2(-9. 8)(yf– 0) yf =-150. 52/2/-9. 8 = 1155 m/s xf = ? t=? Equation has xf, t yf = ? vf = 0 t = 1. 14 Equation has t Equation has yf, t Equation has yf

Projectile Motion – Example 3 b • • A rifle fires a bullet at a speed of 250 m/s at an angle of 370 above the horizontal. (b) How long is the bullet in the air? Ø Horizontal xf = xi + vt xi = 0 xf = ? v=250 cos(37)=199. 7 t = ? xf = 0 + 199. 7 t Equation has xf, t Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 0 vi = 250 sin(37)=150. 5 vf = ? a = -9. 8 t=? vf = 150. 5 – 9. 8 t Equation has vf, t 0 = 0 + 150. 5 t + ½(-9. 8)t 2 Equation has t vf 2 = 150. 52+2(-9. 8)(0– 0) Equation has vf 0 = 0 + 150. 5 t + ½(-9. 8)t 2 t = -150. 5(2)/-9. 8 = 30. 7 s

Projectile Motion – Example 3 c • • A rifle fires a bullet at a speed of 250 m/s at an angle of 370 above the horizontal. (b) What is the balls range? Ø Horizontal xf = xi + vt xi = 0 xf = ? v=250 cos(37)=199. 7 t = 30. 7 xf = 0 + 199. 7(30. 7) Equation has xf Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 0 vi = 250 sin(37)=150. 5 vf = ? a = -9. 8 t = 30. 7 vf = 150. 5 – 9. 8(30. 7) Equation has vf 0=0+150. 5(30. 7)+½(-9. 8)(30. 7)2 Can’t use equation vf 2 = 150. 52+2(-9. 8)(0– 0) Equation has vf xf = 0 + 199. 7(30. 7) = 6130. 8 m

2 -Dimension Projectile Motion – Example 4 a (Find Time) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 9 degrees to the horizontal • (a) Find height at which it hits fence at distance 180 m? • Horizontal xf = xi + vt xi = 0 xf = 180 v = 50 cos 36. 9 = 40 t = ? 180 = 0 + 40 t t = 180 / 40 = 4. 5 s Equation has t

Projectile Motion – Example 4 a (Find Height) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 9 degrees to the horizontal • (a) Find height at which it hits fence at distance 180 m? Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = ? vi = 50 sin 36. 9=30 vf = ? a = -9. 8 t = 4. 5 vf = 30 – 9. 8(4. 5) Equation has vf yf = 0 + 30(4. 5) + ½(-9. 8)(4. 5)2 Equation has yi vf 2 = 302+2(-9. 8)(yf – 0) Equation has yf, vf yf = 0 + 30(4. 5) + ½(-9. 8)(4. 5)2 = 35. 8 m

2 -Dimensions Projectile Motion – Example 4 b (Find Velocity 1) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 9 degrees to the horizontal • (b) What is velocity at which it hits a fence at distance of 180 m? Ø Vertical vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 35. 8 vi = 50 sin 36. 9=30 vf = ? a = -9. 8 t = 4. 5 vf = 30 – 9. 8(4. 5) Equation has vf 35. 8 = 0 + 30(4. 5) + ½(-9. 8)(4. 5)2 Can’t use equation vf 2 = 302+2(-9. 8)(35. 8 – 0) Equation has vf = 30 – 9. 8(4. 5) = -14. 1 m/s

2 -Dimensions Projectile Motion – Example 4 b (Find Velocity 2) • Batter hits a ball giving it a velocity of 50 m/s • At an angle of 36. 90 to the horizontal • (b) What is velocity at which it hits a fence at distance of 180 m? Øvy = -14. 1 m/s Øvx = 40 Øv = sqrt(402 + (-14. 1)2) = 42. 4 m/s Øq = tan-1(14. 1/40) = 19. 10 Øvy is negative, therefore q points into fourth quadrant