PHY 151 Lecture 12 12 1 Motion of

PHY 151: Lecture 12 • • 12. 1 Motion of an Object attached to a Spring 12. 2 Particle in Simple Harmonic Motion 12. 3 Energy of the Simple Harmonic Oscillator 12. 4 The Simple Pendulum 12. 5 The Physical Pendulum 12. 6 Damped Oscillations 12. 7 Forced Oscillations 12. 8 Context Connection: Resonance in Structures

PHY 151: Lecture 12 Oscillatory Motion 12. 1 Motion of an Object Attached to a Spring

Motion of an Object Attached to a Spring - 1 • Periodic motion is the motion of an object that regularly repeats • The object returns to a given position after a fixed time interval • A special kind of periodic motion occurs in mechanical systems when the force acting on the object is proportional to the position of the object relative to some equilibrium position • If the force is always directed toward the equilibrium position, the motion is called simple harmonic motion

Motion of an Object Attached to a Spring - 2 • A block of mass m is attached to a spring, the block is free to move on a frictionless horizontal surface • When the spring is neither stretched nor compressed, the block is at the equilibrium position

Motion of an Object Attached to a Spring- 3 • Hooke’s Law states • Fs is the linear restoring force • It is always directed toward the equilibrium position • Therefore, it is always opposite the displacement from equilibrium – k is the force (spring) constant – x is the displacement

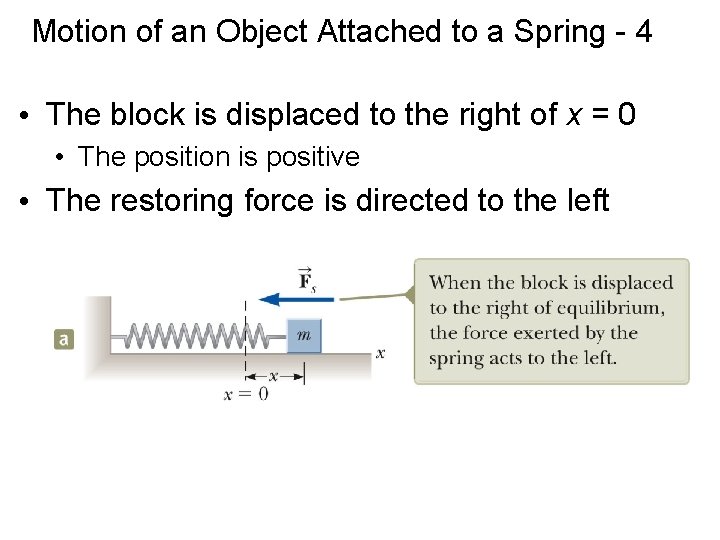
Motion of an Object Attached to a Spring - 4 • The block is displaced to the right of x = 0 • The position is positive • The restoring force is directed to the left

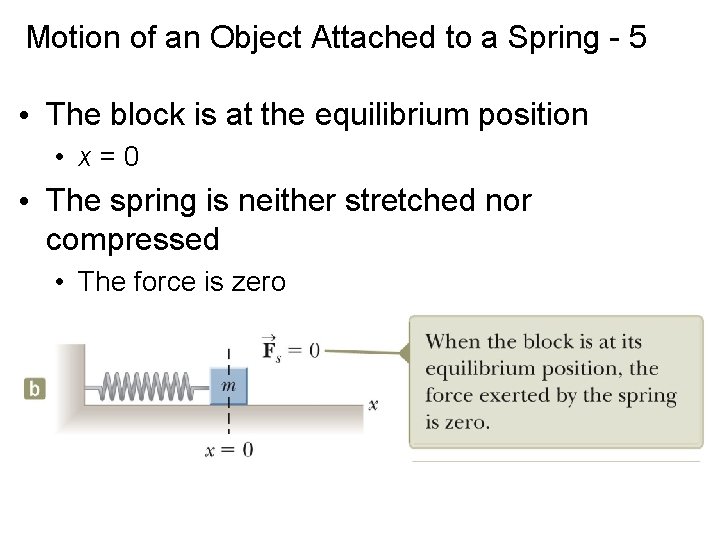
Motion of an Object Attached to a Spring - 5 • The block is at the equilibrium position • x=0 • The spring is neither stretched nor compressed • The force is zero

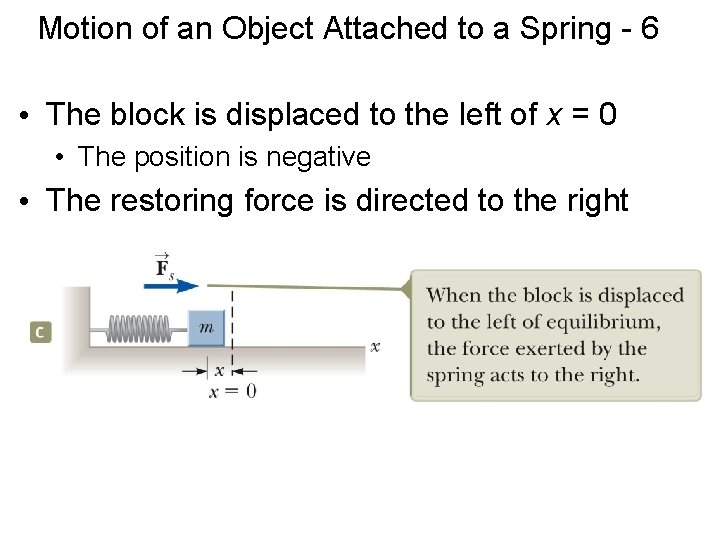
Motion of an Object Attached to a Spring - 6 • The block is displaced to the left of x = 0 • The position is negative • The restoring force is directed to the right

Motion of an Object Attached to a Spring - 7 • The force described by Hooke’s law is the net force in Newton’s second law

Motion of an Object Attached to a Spring - 8 • The acceleration is proportional to the displacement of the block • The direction of the acceleration is opposite the direction of the displacement from equilibrium • An object moves with simple harmonic motion whenever its acceleration is proportional to its position and is oppositely directed to the displacement from equilibrium

Motion of an Object Attached to a Spring - 9 • The acceleration is not constant, so kinematic equations cannot be applied • If the block is released from some position = A, then the initial acceleration is –k. A/m • Its speed is zero – When the block passes through the equilibrium position, a = 0 • Its speed is a maximum – The block continues to x = –A where its acceleration is +k. A/m x

Motion of an Object Attached to a Spring - 10 • The block continues to oscillate between –A and +A – These are turning points of the motion • The force is conservative • In the absence of friction, the motion will continue forever – Real systems are generally subject to friction, so they do not actually oscillate forever

PHY 151: Lecture 12 Oscillatory Motion 12. 2 Particle in Simple Harmonic Motion

Particle in Simple Harmonic Motion - 1 • Simple harmonic motion can be represented mathematically: • So • Let • Then

Particle in Simple Harmonic Motion - 2 • A function that satisfies the equation is needed • Need a function x(t) whose second derivative is the same as the original function with a negative sign and multiplied by w 2 • The sine and cosine functions meet these requirements

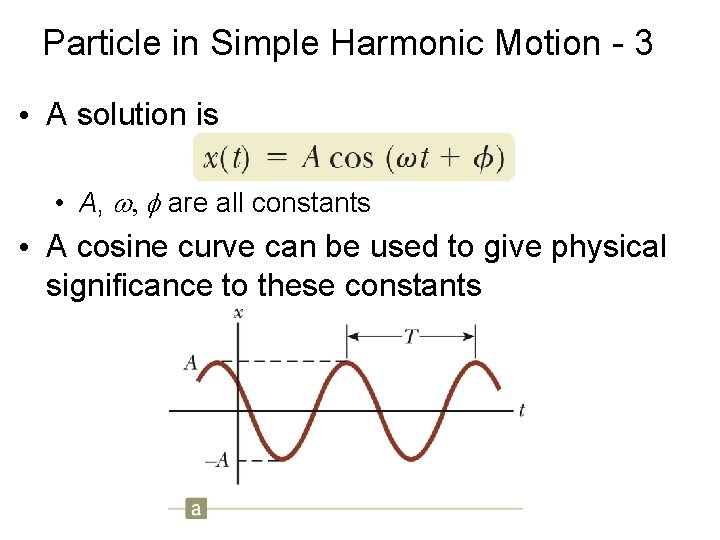
Particle in Simple Harmonic Motion - 3 • A solution is • A, w, f are all constants • A cosine curve can be used to give physical significance to these constants

Particle in Simple Harmonic Motion - 4 • A is the amplitude of the motion • This is the maximum position of the particle in either the positive or negative direction • w is called the angular frequency • Units are rad/s • f is the phase constant or the initial phase angle • We can now define a new analysis model: • the particle in simple harmonic motion model

Particle in Simple Harmonic Motion - 5 • A and f are determined uniquely by the position and velocity of the particle at t = 0 • If the particle is at x = A at t = 0, then f = 0 • The phase of the motion is the quantity (w t + f ) • x (t) is periodic and its value is the same each time wt increases by 2 radians

Particle in Simple Harmonic Motion - 6 • The period, T, is the time interval required for the particle to go through one full cycle of its motion • The values of x and v for the particle at time t equal the values of x and v at t + T

Particle in Simple Harmonic Motion -7 • The inverse of the period is called the frequency • The frequency represents the number of oscillations that the particle undergoes per unit time interval • Units are cycles per second = hertz (Hz)

Particle in Simple Harmonic Motion- 8 • The frequency and period equations can be rewritten to solve for w • The period and frequency can also be expressed as

Particle in Simple Harmonic Motion - 9 • The frequency and the period depend only on the mass of the particle and the force constant of the spring • They do not depend on the parameters of motion • The frequency is larger for a stiffer spring (large values of k) and decreases with increasing mass of the particle

Particle in Simple Harmonic Motion - 10 • The equations are:

Particle in Simple Harmonic Motion - 11 • Because the sine and cosine functions oscillate between ± 1, we can find the maximum values of velocity and acceleration for an object in SHM:

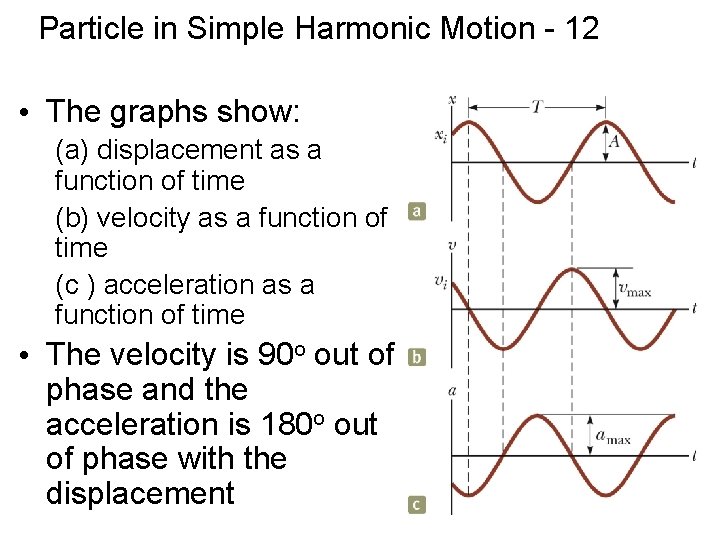
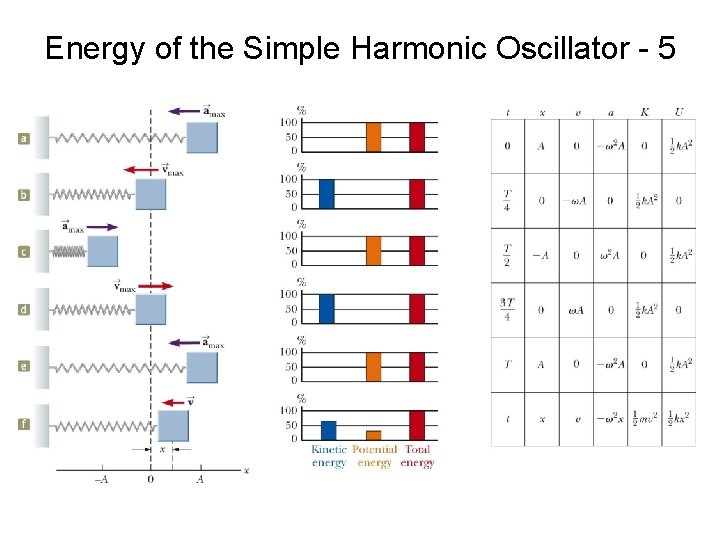
Particle in Simple Harmonic Motion - 12 • The graphs show: (a) displacement as a function of time (b) velocity as a function of time (c ) acceleration as a function of time • The velocity is 90 o out of phase and the acceleration is 180 o out of phase with the displacement

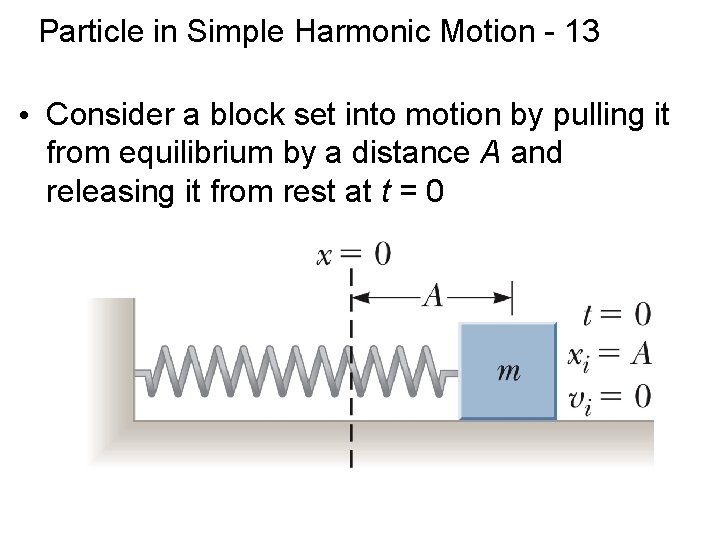
Particle in Simple Harmonic Motion - 13 • Consider a block set into motion by pulling it from equilibrium by a distance A and releasing it from rest at t = 0

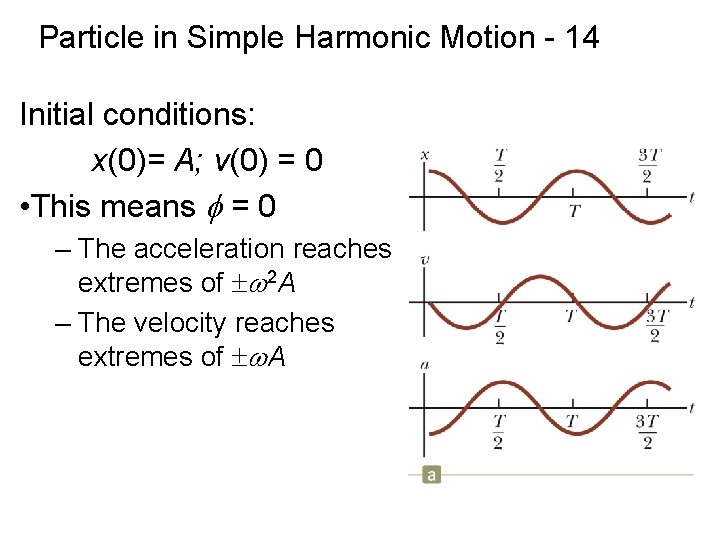
Particle in Simple Harmonic Motion - 14 Initial conditions: x(0)= A; v(0) = 0 • This means f = 0 – The acceleration reaches extremes of ±w 2 A – The velocity reaches extremes of ±w. A

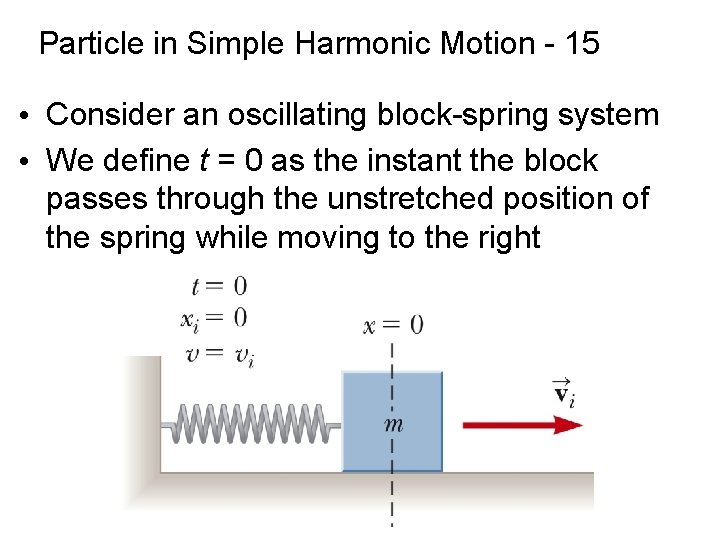
Particle in Simple Harmonic Motion - 15 • Consider an oscillating block-spring system • We define t = 0 as the instant the block passes through the unstretched position of the spring while moving to the right

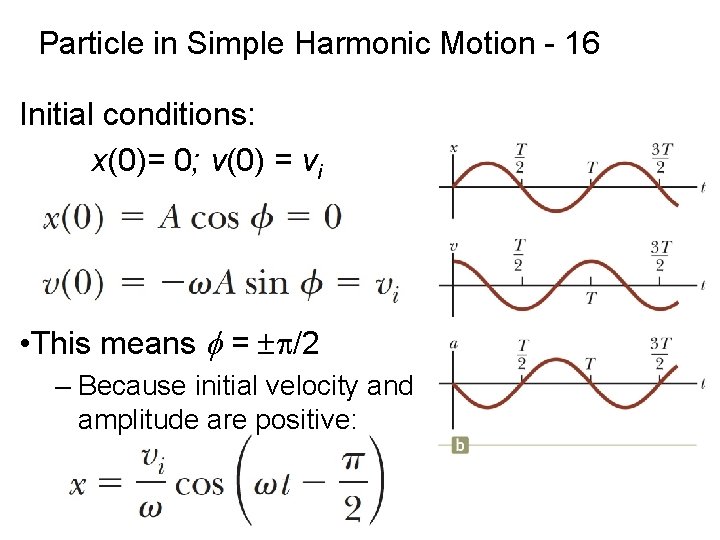
Particle in Simple Harmonic Motion - 16 Initial conditions: x(0)= 0; v(0) = vi • This means f = ± /2 – Because initial velocity and amplitude are positive:

Example 12. 1 A 200 -g block connected to a light spring for which the force constant is 5. 00 N/m is free to oscillate on a frictionless, horizontal surface. The block is displaced 5. 00 cm from equilibrium and released from rest.

Example 12. 1 (A) Find the period of its motion • Find the angular frequency: • Find the period:

Example 12. 1 (B) Determine the maximum speed of the block. • Find vmax: (C) What is the maximum acceleration of the block? • Find amax:

Example 12. 1 (D) Express the position, velocity, and acceleration as functions of time in SI units. • Find the phase constant: • Write an expression for x(t): • Write an expression for v(t): • Write an expression for a(t):

Example 12. 2 A car with a mass of 1300 kg is constructed so that its frame is supported by four springs. Each spring has a force constant of 20 000 N/m. Two people riding in the car have a combined mass of 160 kg. Find the frequency of vibration of the car after it is driven over a pothole in the road.

Example 12. 2 • Find an expression for the total force on the car: • Evaluate the effective spring constant: • Find the frequency of vibration:

PHY 151: Lecture 12 Oscillatory Motion 12. 3 Energy of the Simple Harmonic Oscillator

Energy of the Simple Harmonic Oscillator - 1 • Assume a spring-mass system is moving on a frictionless surface • This is an isolated system, so the total energy is constant • The kinetic energy is • The elastic potential energy is

Energy of the Simple Harmonic Oscillator - 2 • The total energy is • Using sin 2 + cos 2 = 1:

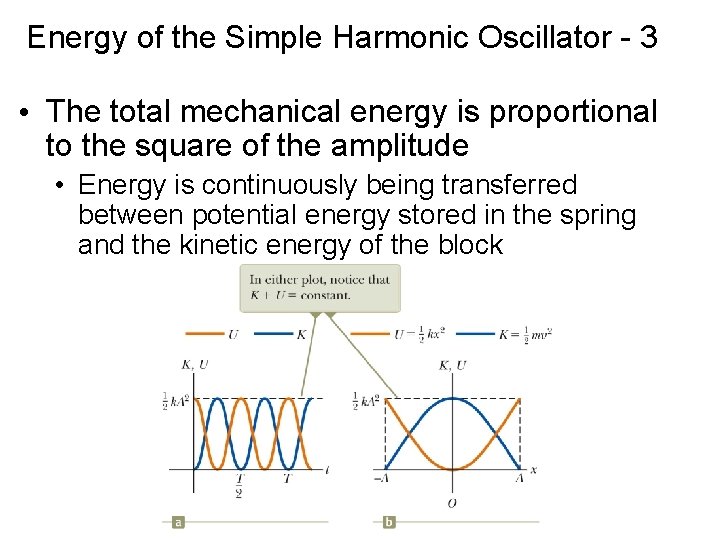
Energy of the Simple Harmonic Oscillator - 3 • The total mechanical energy is proportional to the square of the amplitude • Energy is continuously being transferred between potential energy stored in the spring and the kinetic energy of the block

Energy of the Simple Harmonic Oscillator - 4 • Energy can be used to find the velocity:

Energy of the Simple Harmonic Oscillator - 5

Example 12. 3 A 0. 500 -kg cart connected to a light spring for which the force constant is 20. 0 N/m oscillates on a frictionless, horizontal air track.

Example 12. 3 (A) Calculate the maximum speed of the cart if the amplitude of the motion is 3. 00 cm. • Equate the total energy to the kinetic energy when cart is at x = 0: • Solve for vmax and substitute numerical values:

Example 12. 3 (B) What is the velocity of the cart when the position is 2. 00 cm? • Evaluate the velocity:

Example 12. 3 (C) Compute the kinetic and potential energies of the system when the position of the cart is 2. 00 cm. • Evaluate the kinetic energy: • Evaluate the elastic potential energy:

PHY 151: Lecture 12 Oscillatory Motion 12. 4 The Simple Pendulum

The Simple Pendulum - 1 • A simple pendulum also exhibits periodic motion • Consists of an object of mass m suspended by a light string or rod of length L • The upper end of the string is fixed • When the object is pulled to the side and released, it oscillates about the lowest point, which is the equilibrium position • The motion occurs in the vertical plane and is driven by the gravitational force

The Simple Pendulum - 2 • Equation of motion in the tangential direction is which reduces to

The Simple Pendulum - 3 • Assuming is small, use the small angle approximation (sin » ): • The angular frequency is • The period is

Simple Pendulum - 4 • The period and frequency of a simple pendulum depend only on the length of the string and the acceleration due to gravity • The period is independent of the mass • All simple pendula that are of equal length and are at the same location oscillate with the same period

Example 12. 4 Christian Huygens (1629– 1695), the greatest clockmaker in history, suggested that an international unit of length could be defined as the length of a simple pendulum having a period of exactly 1 s. How much shorter would our length unit be if his suggestion had been followed? – Solve for length and substitute values:

PHY 151: Lecture 12 Oscillatory Motion 12. 5 The Physical Pendulum Skipped

PHY 151: Lecture 12 Oscillatory Motion 12. 6 Damped Oscillations Skipped

PHY 151: Lecture 12 Oscillatory Motion 12. 7 Forced Oscillations Skipped