Phenotypic factor analysis Conor Dolan Mike Neale Michel





















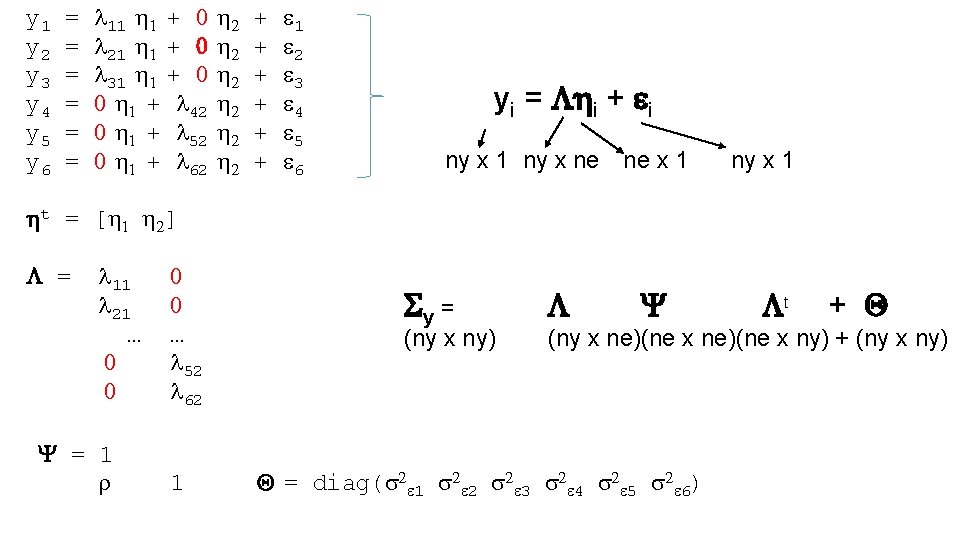


![The model for the Yi = b 0 + b 1*Xi + ei E[Y|X=x˚] The model for the Yi = b 0 + b 1*Xi + ei E[Y|X=x˚]](https://slidetodoc.com/presentation_image_h/36b3c9e36cc32442be9117399f8b10ad/image-49.jpg)
- Slides: 50

Phenotypic factor analysis Conor Dolan, Mike Neale, & Michel Nivard

Factor analysis Part I: The linear factor model as a statistical (regression) model - formal representation as a causal – psychometric - model (vs data reduction) - what is a common factor substantively? - implication in terms of data summary and causal modeling - why is the phenotypic factor model relevant to genetic modeling? - what can we learn about the phenotypic common factors from twin data?

If you understand linear regression, you understand a key ingredient of the linear factor model (as a statistical model). If you understand logistic linear regression, you understand a key ingredient of the ordinal factor model (as a statistical model).

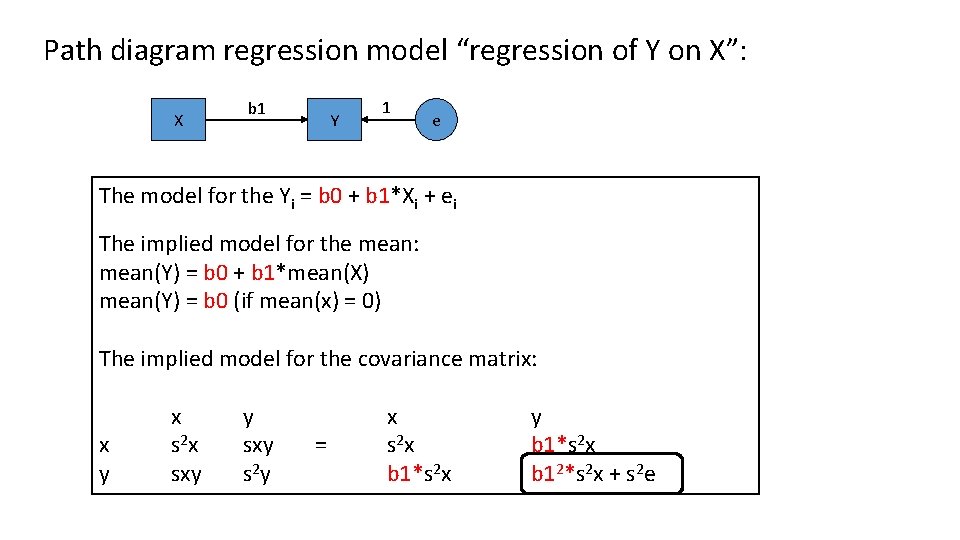
Path diagram regression model “regression of Y on X”: X b 1 Y 1 e The model for the Yi = b 0 + b 1*Xi + ei The implied model for the mean: mean(Y) = b 0 + b 1*mean(X) mean(Y) = b 0 (if mean(x) = 0) The implied model for the covariance matrix: x y x s 2 x sxy y sxy s 2 y = x s 2 x b 1*s 2 x y b 1*s 2 x b 12*s 2 x + s 2 e

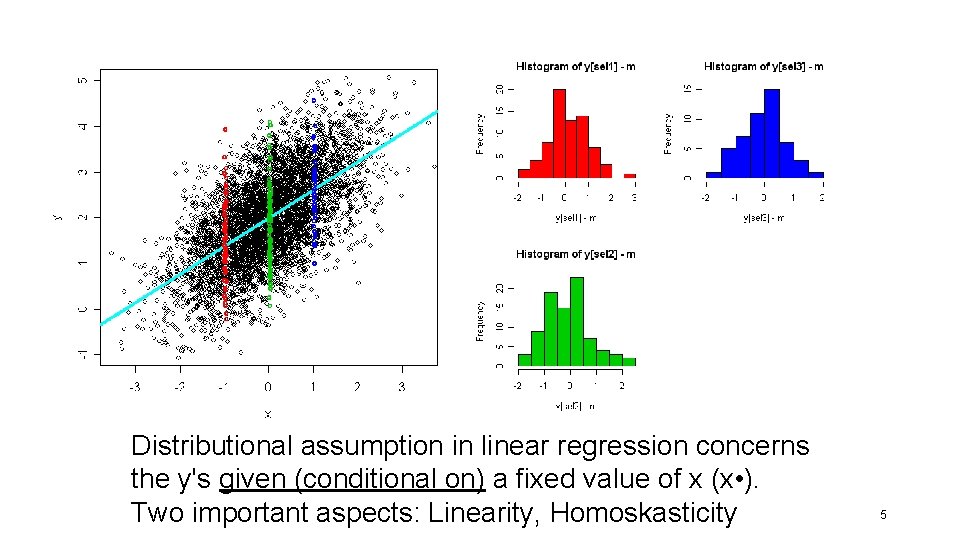
Distributional assumption in linear regression concerns the y's given (conditional on) a fixed value of x (x • ). Two important aspects: Linearity, Homoskasticity 5

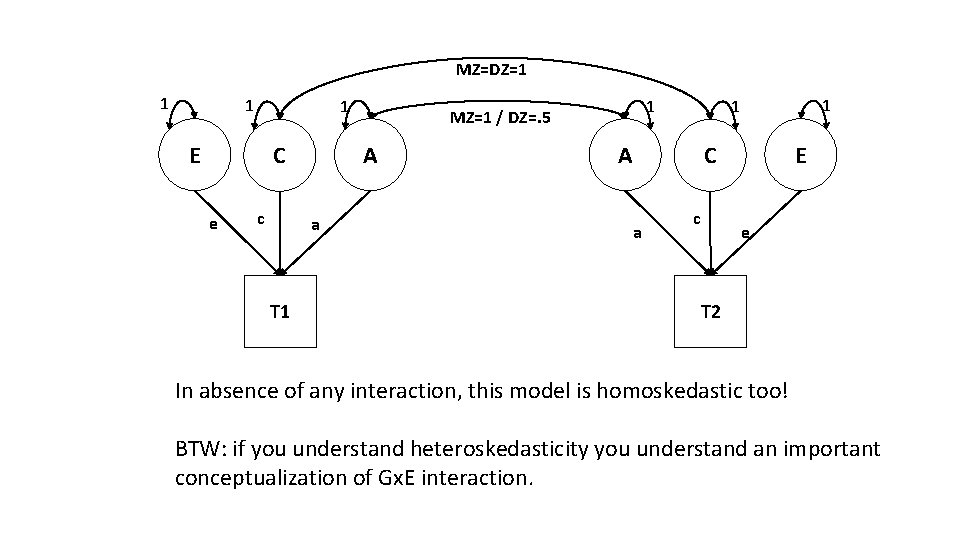
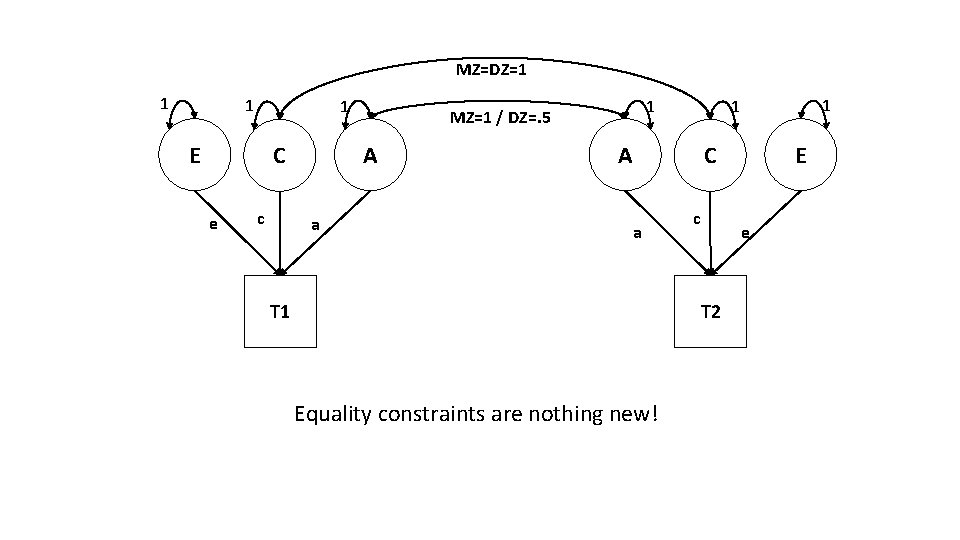
MZ=DZ=1 1 E A C e c a T 1 1 MZ=1 / DZ=. 5 1 1 A E C a c e T 2 In absence of any interaction, this model is homoskedastic too! BTW: if you understand heteroskedasticity you understand an important conceptualization of Gx. E interaction.

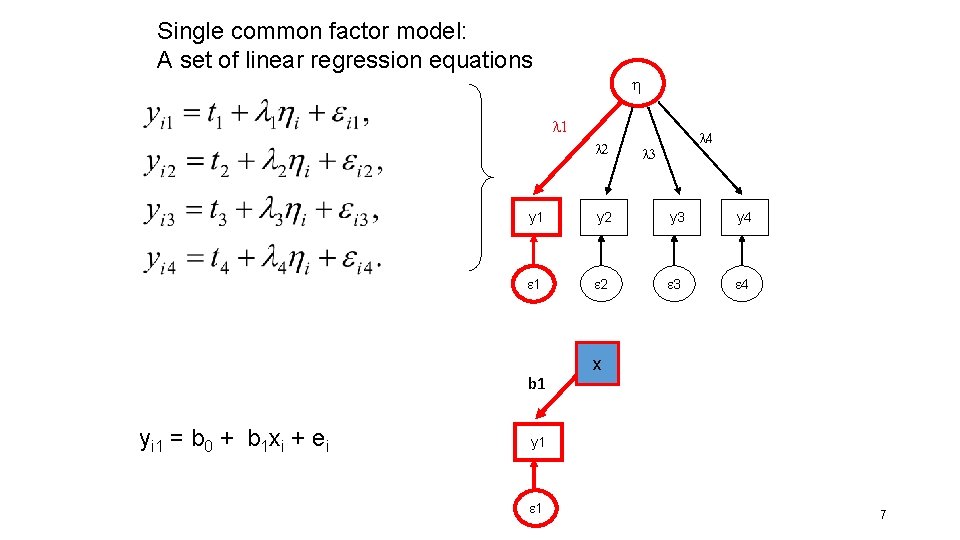
Single common factor model: A set of linear regression equations l 1 l 2 l 3 y 1 y 2 y 3 y 4 1 2 3 4 b 1 yi 1 = b 0 + b 1 xi + ei l 4 x y 1 1 7

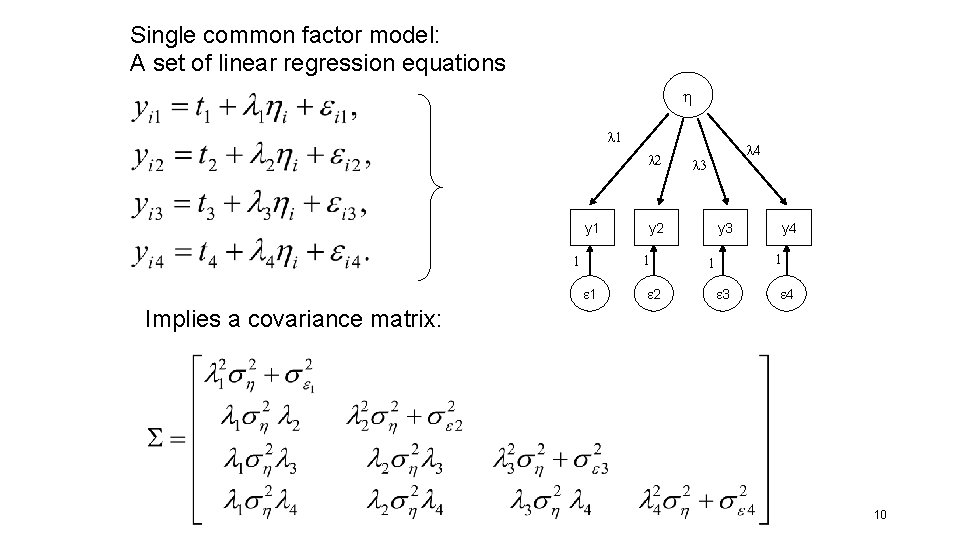
yi 1 =t 1 + l 1 i + ei l The implied model for the covariance matrix: y s 2 l 1 s 2 y l 1 s 2 l 1 2 s 2 + s 2 y 1 1 Mean(y 1)= t 1 + l 1 Mean( ) = t 1 R 2 = (l 12 * s 2 ) / (l 12 * s 2 + s 2 ) 8

But what is the point if the common factor (the independent variable, ) is not observed? 9

Single common factor model: A set of linear regression equations l 1 l 2 y 1 1 l 3 y 2 1 1 l 4 2 y 3 y 4 1 1 3 4 Implies a covariance matrix: 10

A set of linear regression coefficients expressed as a single matrix equation: using matrix algebra yi – t = i + i Matrix algebra is 1) Notationally Efficient 2) Basis of Multivariate Statistics (useful to know!) 11

ny number of variables ne number of common factors yi – t = i + i ny x 1 ny x ne ne x 1 ti = t 1 y i = t 2 t 3 t 4 yi 1 yi 2 yi 3 yi 4 i = i 1 i 2 i 3 i 4 ny x 1 = l 1 l 2 l 3 l 4 ny x 1 i = i 1 x 1 12

ny number of variables ne number of common factors yi = i + i ny x 1 ny x ne ne x 1 Centered t = 0! ny x 1 s 2 y 1 = E[y 1 y 1] = E[(l 1 i + i )] = E[(l 1 i + l 1 i i + il 1 i + i i )] = E[l 1 i] + E[l 1 i i] + E[ il 1 i] + E[ i i ] = l 1 l 1 E[ i i] + E[ i i ] = l 12 s 2 + s 2 13

ny number of variables ne number of common factors yi = i + I ny x 1 ny x ne ne x 1 Sy = E[y*yt] = E[( i + i)t] = E[( i + i)( it t + it)] = E[ i it t + i it + i it ] = E[ i it t ] + E[ i it t] + E[ i it ] = E[ i it] t + E[ i it ] + E[ i it] t + E[ i it ] = Sy = E[ i it] t + E[ i it ] = Y t + Q Centered t = 0! ny x 1 (1) (2) (3) (4) (5) (6) 14

ny number of variables ne number of common factors yi = i + i ny x 1 ny x ne ne x 1 ny x 1 Sy = E[yyt] = E[( i + i)t] = Y t + Q E[ i it] = Y and E[ i it] = Q You can represent this model in Open. Mx using matrices 15

So what? What is the use?

Depression items • • • • I feel lonely I feel confused or in a fog I cry a lot I worry about my future. I am afraid I might think or do something bad I feel that I have to be perfect I feel that no one loves me I feel worthless or inferior I am nervous or tense I lack self confidence I am too fearful or anxious I feel too guilty I am self-conscious or easily embarrassed I am unhappy, sad or depressed I worry a lot I am too concerned about how I look I worry about my relations with the opposite sex Are the data consistent with the presence of a latent construct that underlies the observed variables (items) and that accounts for the inter-correlations between variables?

The use is to test the hypothesis that the linear relations among my 4 indicators of neuroticism, as expressed in the correlation or covariance matrix, are consistent with the presence of a single common influence, the latent variable “neuroticism”.

n 3 n 4 n 5 n 6 n 3 35. 376 15. 807 4. 956 19. 023 n 4 0. 624 18. 159 2. 668 11. 654 n 5 0. 204 0. 154 16. 640 4. 274 N=361, Female 1 st year psychology students n 6 0. 685 0. 586 0. 225 21. 769 ? 19

# datf=read. table('rdataf') colnames(datf)=c('sex', 'n 1', 'n 2', 'n 3', 'n 4', 'n 5', 'n 6', 'e 1', 'e 2', 'e 3', 'e 4', 'e 5', 'e 6', 'o 1', 'o 2', 'o 3', 'o 4', 'o 5', 'o 6', 'a 1', 'a 2', 'a 3', 'a 4', 'a 5', 'a 6', 'c 1', 'c 2', 'c 3', 'c 4', 'c 5', 'c 6') datf_n 4=datf[, 4: 7] Sn 4=cov(datf_n 4) round(Sn 4, 3) fa 1=factanal(covmat=Sn 4, n. obs=361, factors=1) # library(Open. Mx) datf_n 4=as. data. frame(datf_n 4) ny=4 selvars=colnames(datf_n 4) # Rn 4=mx. Matrix(type='Stand', nrow=ny, ncol=ny, free=TRUE, value=. 5, lbound=-. 9, ubound=. 9, name='corn 4') Sdsn 4=mx. Matrix(type='Diag', nrow=ny, ncol=ny, free=TRUE, value=5, name='sdsn 4') Meann 4=mx. Matrix(type='Full', nrow=1, ncol=ny, free=TRUE, value=20, name='men 4') Mk. S=mx. Algebra(expression=sdsn 4%*%corn 4%*%sdsn 4, name='Ssatn 4') modelp 1=mx. Model('part 1', Rn 4, Sdsn 4, Meann 4, Mk. S) # N 4 model 0=mx. Model("N 4 sat", mx. Data( observed=datf, type="raw"), # the data mx. FIMLObjective( covariance="part 1. Ssatn 4", means="part 1. men 4", dimnames=selvars) # the fit function ) Model 1 <- mx. Model("model 1", modelp 1, N 4 model 0, mx. Algebra(N 4 sat. objective, name="minus 2 loglikelihood"), mx. Algebra. Objective("minus 2 loglikelihood")) # fit the model Model 1_o <- mx. Run(Model 1) # Ly=mx. Matrix(type='Full', nrow=ny, ncol=1, free=TRUE, value=1, name='Ly') Te=mx. Matrix(type='Diag', nrow=ny, ncol=ny, free=TRUE, value=5, name='Te') Ps=mx. Matrix(type='Symm', nrow=1, ncol=1, free=FALSE, value=1, name='Ps') Meann 4=mx. Matrix(type='Full', nrow=1, ncol=ny, free=TRUE, value=20, name='men 4') Mk. S=mx. Algebra(expression=Ly%*%Ps%*%t(Ly)+Te, name='S 1 fn 4') # modelp 1=mx. Model('part 1', Ly, Te, Ps, Meann 4, Mk. S) # N 4 model 2=mx. Model("N 4 f 1", mx. Data( observed=datf, type="raw"), # the data mx. FIMLObjective( covariance="part 1. S 1 fn 4", means="part 1. men 4", dimnames=selvars) # the fit function # ) Model 2 <- mx. Model("model 1", modelp 1, N 4 model 2, mx. Algebra(N 4 f 1. objective, name="minus 2 loglikelihood"), mx. Algebra. Objective("minus 2 loglikelihood")) # fit the model Model 2_o <- mx. Run(Model 2) Mx. Compare(Model 1_o, Model 2_o) The chi 2 goodness of fit test (c 2=1. 36, df=2) suggest that the model fits well. The observed covariance structure is consistent with my theory. Does this prove the presence of the latent variable? necessary but not sufficient…. Why df=2? Count the observed statistics (S), and the estimated parameters (P): df = S-P.

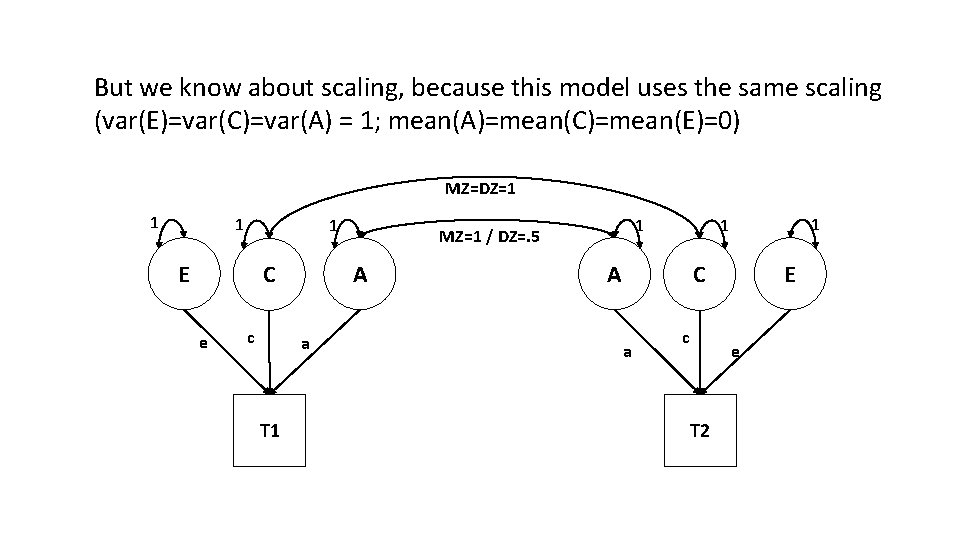
A technical aspect of the common factor model: scaling. The mean and variance of the common factor? The common factor is latent! Scale by setting the mean to zero. (m = 0) Scale by fixing variance to “sensible value” (s 2 = 1) Scale by making it dependent on an indicator by fixing a factor loading to 1 (l 1=1)

But we know about scaling, because this model uses the same scaling (var(E)=var(C)=var(A) = 1; mean(A)=mean(C)=mean(E)=0) MZ=DZ=1 1 E A C e c a T 1 1 MZ=1 / DZ=. 5 1 1 A E C a c e T 2

A technical aspect of the common factor model: scaling. Scale the common factor by fixing to “sensible value” (s 2 = 1)

A technical aspect of the common factor model: scaling. Or making it dependent on an indicator by fixing a factor loading to 1 (l 1=1)

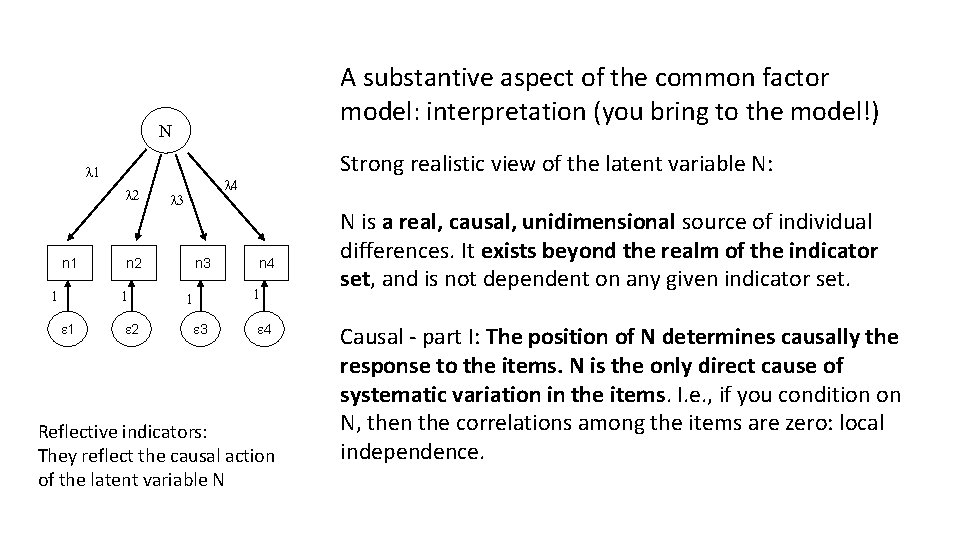
A substantive aspect of the common factor model: interpretation (you bring to the model!) N l 1 l 2 n 1 1 l 4 l 3 n 2 1 1 2 Strong realistic view of the latent variable N: n 3 n 4 1 1 3 4 Reflective indicators: They reflect the causal action of the latent variable N N is a real, causal, unidimensional source of individual differences. It exists beyond the realm of the indicator set, and is not dependent on any given indicator set. Causal - part I: The position of N determines causally the response to the items. N is the only direct cause of systematic variation in the items. I. e. , if you condition on N, then the correlations among the items are zero: local independence.

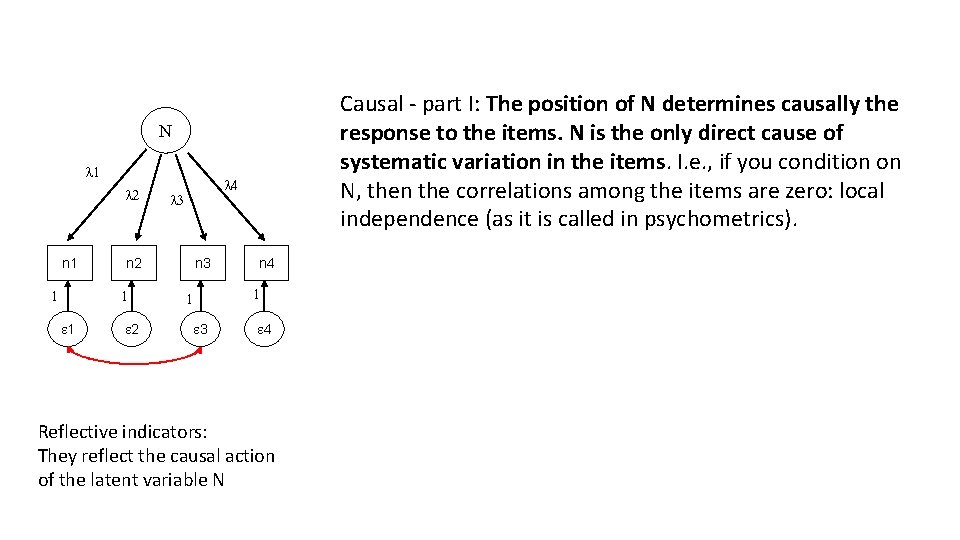
Causal - part I: The position of N determines causally the response to the items. N is the only direct cause of systematic variation in the items. I. e. , if you condition on N, then the correlations among the items are zero: local independence (as it is called in psychometrics). N l 1 l 2 n 1 1 l 3 n 2 1 1 l 4 2 n 3 n 4 1 1 3 4 Reflective indicators: They reflect the causal action of the latent variable N

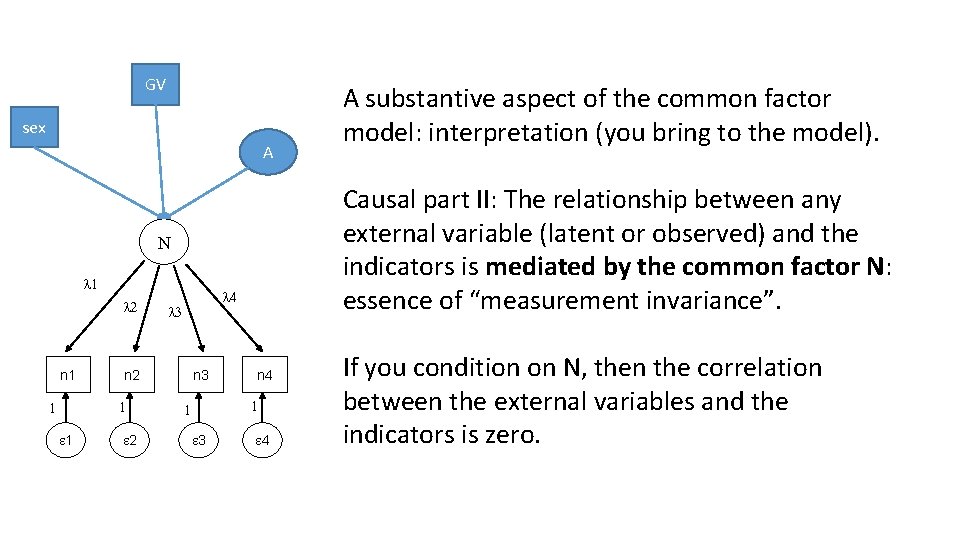
GV sex A Causal part II: The relationship between any external variable (latent or observed) and the indicators is mediated by the common factor N: essence of “measurement invariance”. N l 1 l 2 n 1 n 2 1 1 1 l 4 l 3 2 n 3 n 4 1 1 3 A substantive aspect of the common factor model: interpretation (you bring to the model). 4 If you condition on N, then the correlation between the external variables and the indicators is zero.

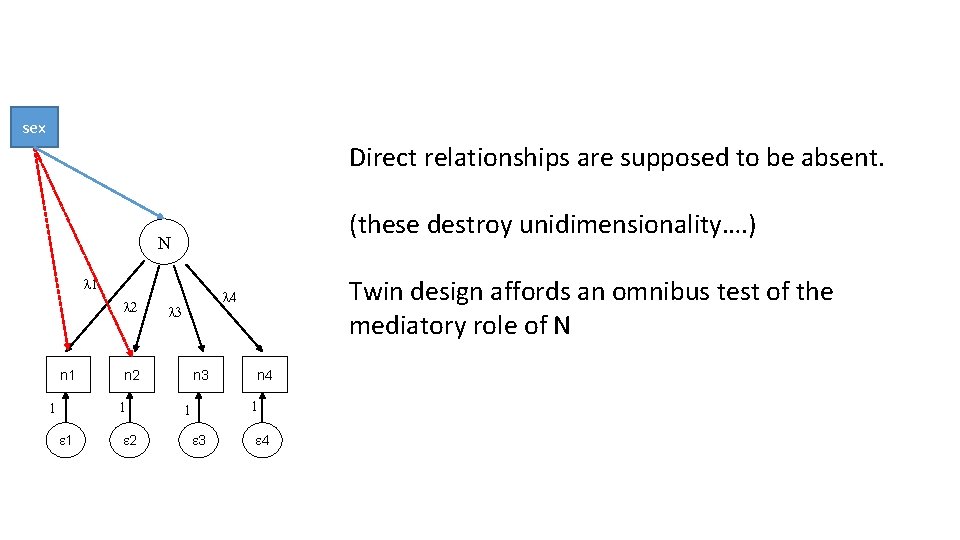
sex Direct relationships are supposed to be absent. (these destroy unidimensionality…. ) N l 1 l 2 n 1 1 l 3 n 2 1 1 2 Twin design affords an omnibus test of the mediatory role of N l 4 n 3 n 4 1 1 3 4

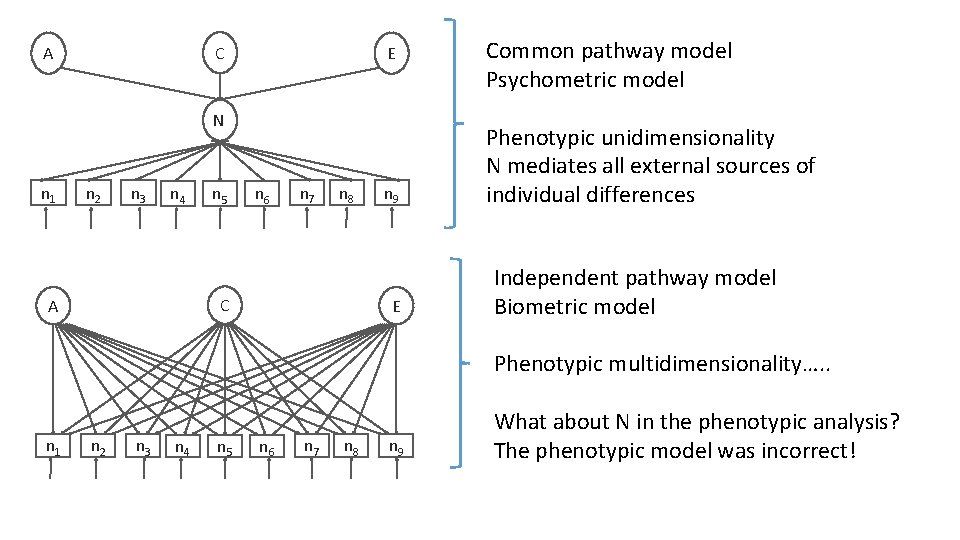
C A E N n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 C A n 9 E Common pathway model Psychometric model Phenotypic unidimensionality N mediates all external sources of individual differences Independent pathway model Biometric model Phenotypic multidimensionality…. . n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 n 9 What about N in the phenotypic analysis? The phenotypic model was incorrect!

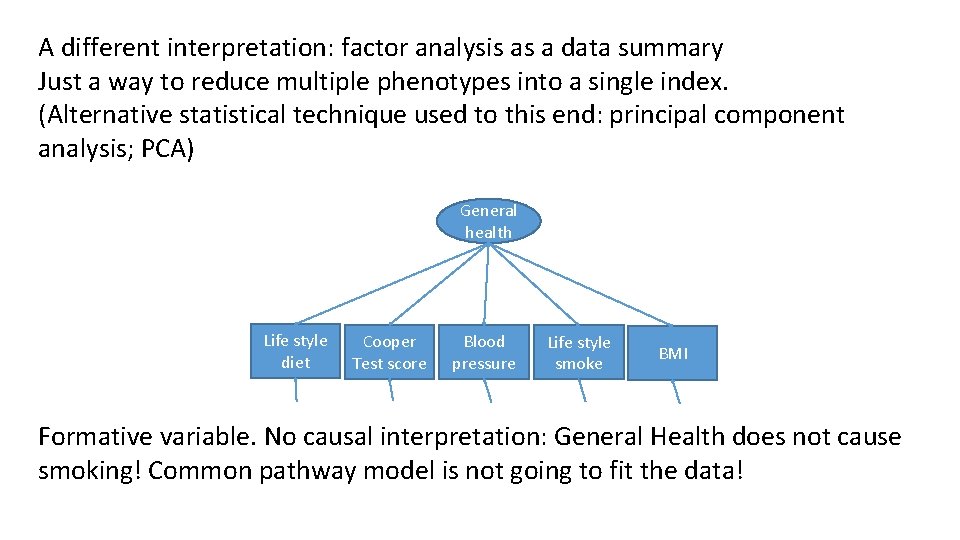
A different interpretation: factor analysis as a data summary Just a way to reduce multiple phenotypes into a single index. (Alternative statistical technique used to this end: principal component analysis; PCA) General health Life style diet Cooper Test score Blood pressure Life style smoke BMI Formative variable. No causal interpretation: General Health does not cause smoking! Common pathway model is not going to fit the data!

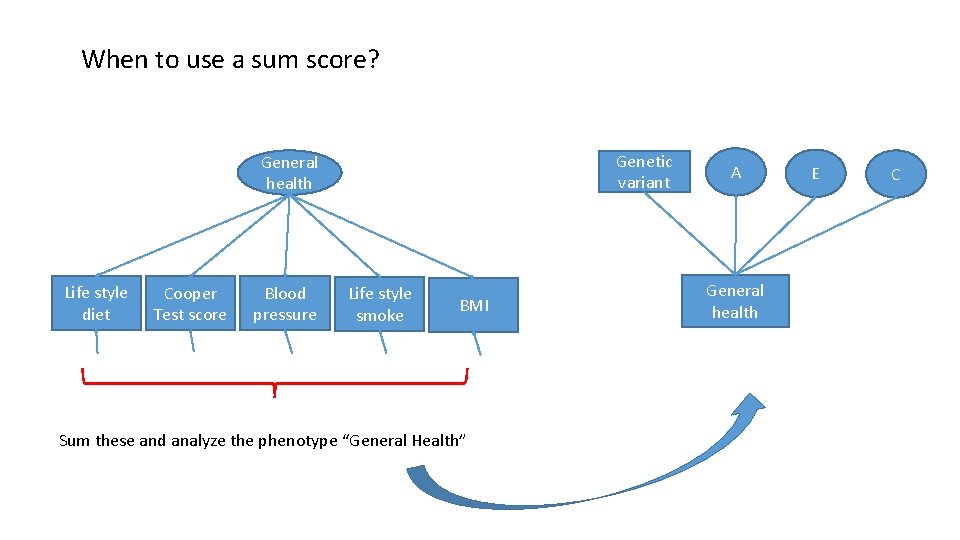
When to use a sum score? Genetic variant General health Life style diet Cooper Test score Blood pressure Life style smoke BMI Sum these and analyze the phenotype “General Health” A General health E C

Back to the common factor model ! Multiple common factors, CFA vs. EFA with rotation EFA (always more than one common factor). Aim: determine dimensionality and derive meaning of factors from loadings Exploratory approach: How many latent variables? What is the pattern of factor loadings? Low on prior theory, but still involves choices. How many latent variables: Screeplot, Eigenvalue > 1 rule, Goodness of fit measures (c 2, RMSEA, NNFI), info criteria (BIC, AIC). Pattern of factor loadings: Type of rotation (varimax, oblimin, many choices!).

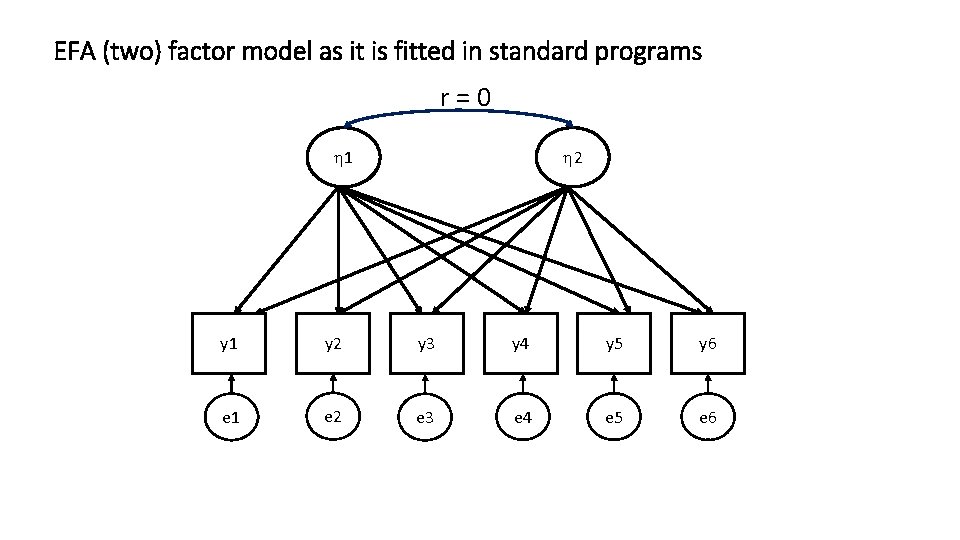
EFA (two) factor model as it is fitted in standard programs r=0 1 2 y 1 y 2 y 3 y 4 y 5 y 6 e 1 e 2 e 3 e 4 e 5 e 6

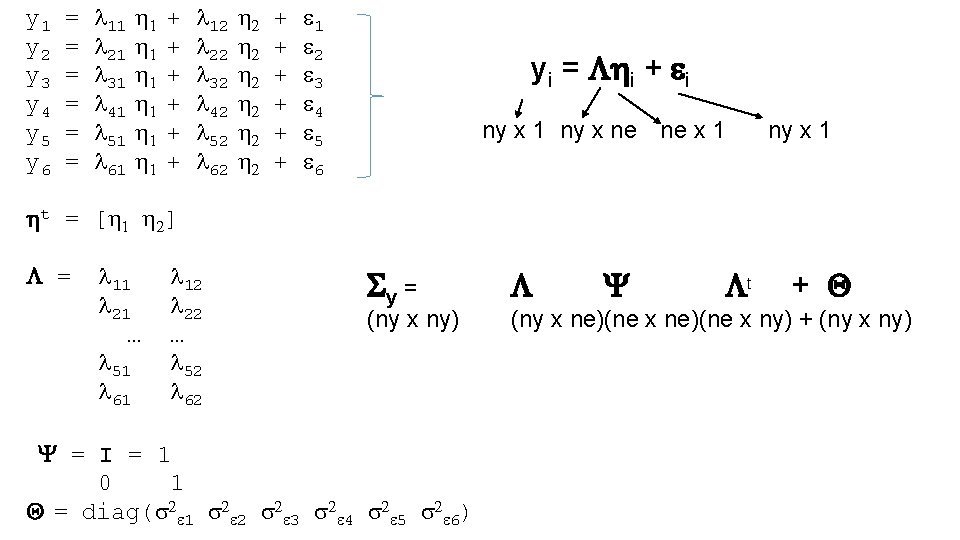
y 1 = l 11 1 + l 12 2 + 1 y 2 = l 21 1 + l 22 2 + 2 y 3 = l 31 1 + l 32 2 + 3 y 4 = l 41 1 + l 42 2 + 4 y 5 = l 51 1 + l 52 2 + 5 y 6 = l 61 1 + l 62 2 + 6 t = [ 1 2] = l 11 l 12 l 21 l 22 … … l 51 l 52 l 61 l 62 yi = i + i ny x 1 ny x ne ne x 1 Sy = (ny x ny) Y = I = 1 0 1 Q = diag(s 2 1 s 2 2 s 2 3 s 2 4 s 2 5 s 2 6) Y t ny x 1 + Q (ny x ne)(ne x ny) + (ny x ny)

y 1 = l 11 1 + l 12 2 + 1 y 2 = l 21 1 + l 22 2 + 2 y 3 = l 31 1 + l 32 2 + 3 y 4 = l 41 1 + l 42 2 + 4 y 5 = l 51 1 + l 52 2 + 5 y 6 = l 61 1 + l 62 2 + 6 Meaning of the common factors? Based on these factor loadings? No! t. Q-1 is diagonal (identifying constraint) Associated with the identifying constraint: unique values of , but rotatable. M = *, MMt = I, so that Sy = MMt t + Q = I t + Q

M = * M: Rotation matrix is calculated by maximizing a rotation criterion. These minimize of maximize loadings to improve interpretability. Orthogonal rotation leaves common factors uncorrelated Oblique rotation allows for correlation. Rotation is just a transformation of results (no testing!). E. g. , test whether factor correlations are 0 is not possible.

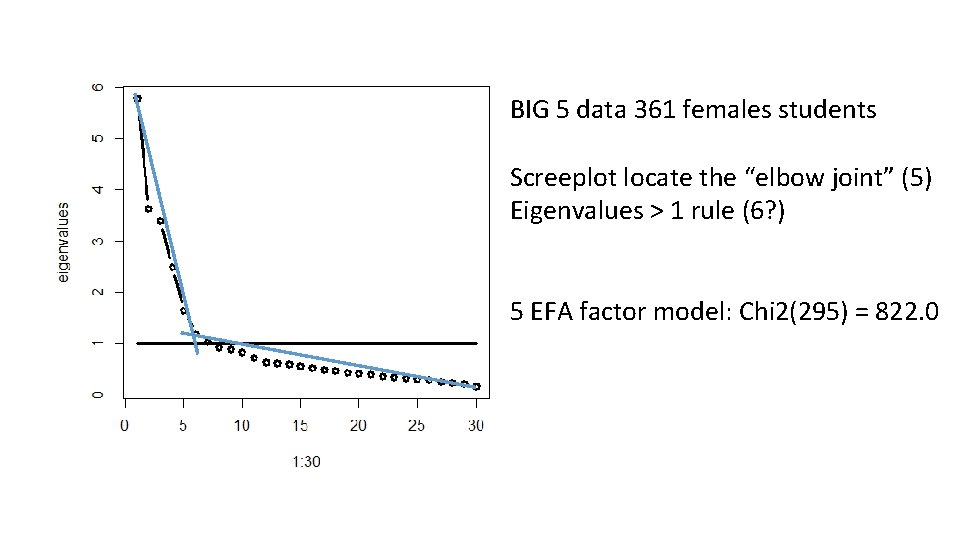
BIG 5 data 361 females students Screeplot locate the “elbow joint” (5) Eigenvalues > 1 rule (6? ) 5 EFA factor model: Chi 2(295) = 822. 0

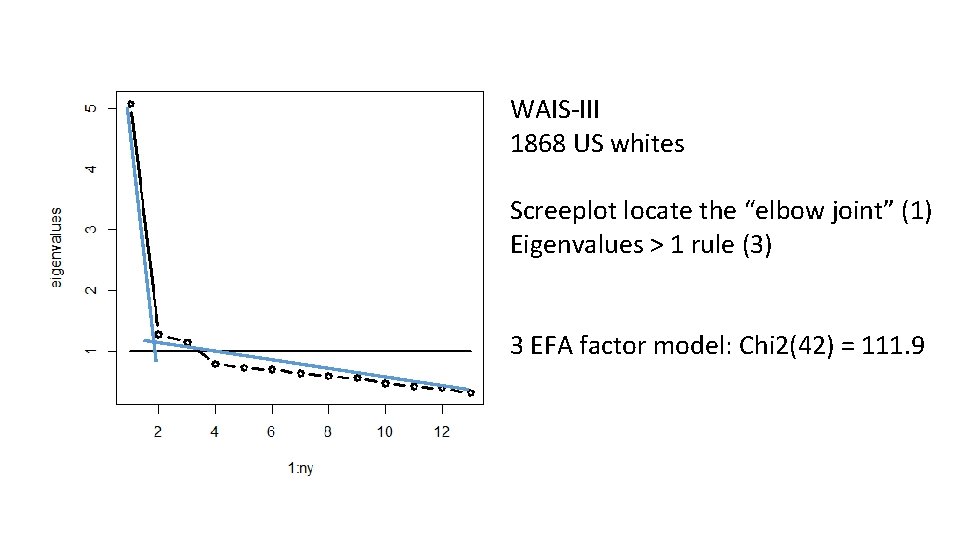
WAIS-III 1868 US whites Screeplot locate the “elbow joint” (1) Eigenvalues > 1 rule (3) 3 EFA factor model: Chi 2(42) = 111. 9

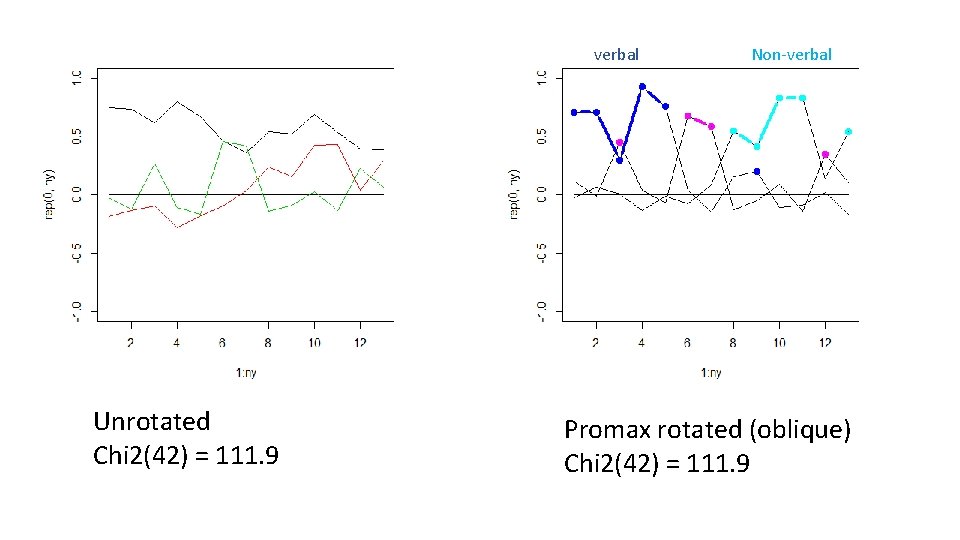
verbal Unrotated Chi 2(42) = 111. 9 Non-verbal Promax rotated (oblique) Chi 2(42) = 111. 9

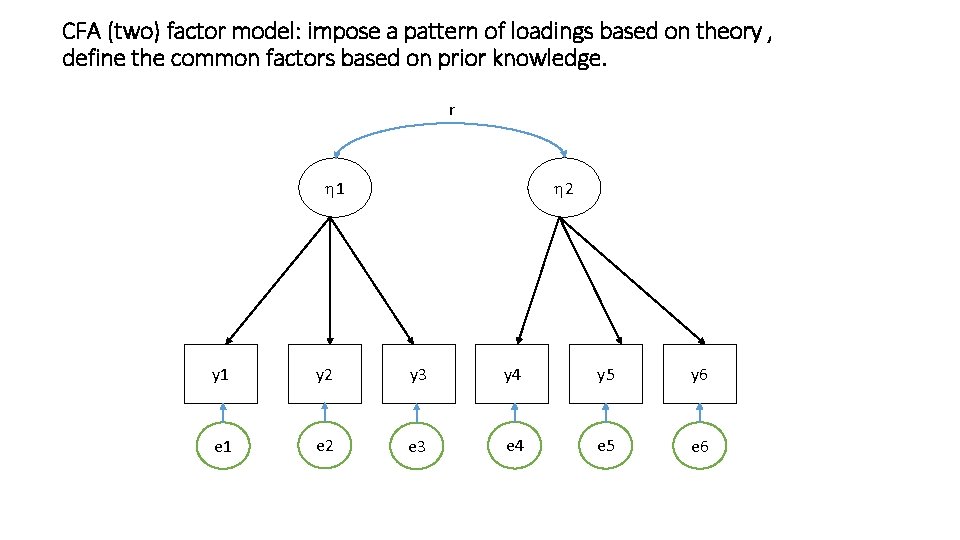
CFA (two) factor model: impose a pattern of loadings based on theory , define the common factors based on prior knowledge. r 1 2 y 1 y 2 y 3 y 4 y 5 y 6 e 1 e 2 e 3 e 4 e 5 e 6
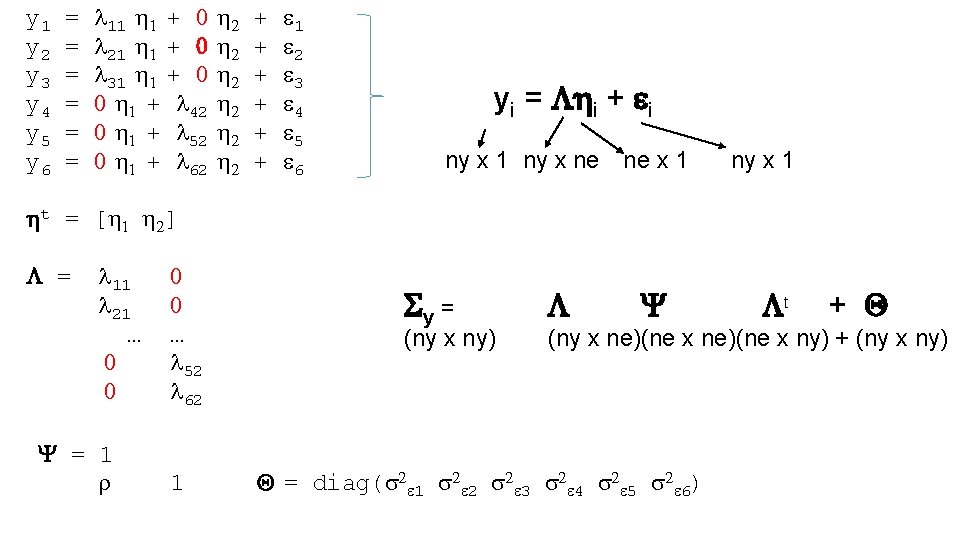
y 1 = l 11 1 + 0 2 + 1 y 2 = l 21 1 + 0 2 + 2 y 3 = l 31 1 + 0 2 + 3 y 4 = 0 1 + l 42 2 + 4 y 5 = 0 1 + l 52 2 + 5 y 6 = 0 1 + l 62 2 + 6 t = [ 1 2] = l 11 0 l 21 0 … … 0 l 52 0 l 62 yi = i + i ny x 1 ny x ne ne x 1 Sy = (ny x ny) Y 1 t + Q (ny x ne)(ne x ny) + (ny x ny) Y = 1 r ny x 1 Q = diag(s 2 1 s 2 2 s 2 3 s 2 4 s 2 5 s 2 6)

Sy = (ny x ny) Y t + Q (ny x ne)(ne x ny) + (ny x ny) In CFA, in contrast to EFA, you can impose all kinds of constraints on the parameters In CFA, in constrast to EFA, you can estimate off-diagonal elements in the cov matrix of the residuals Q

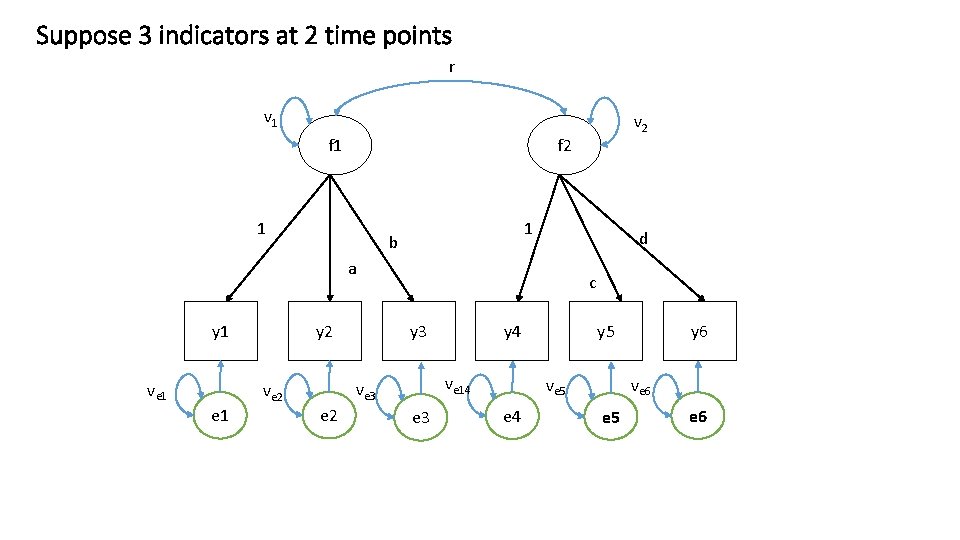
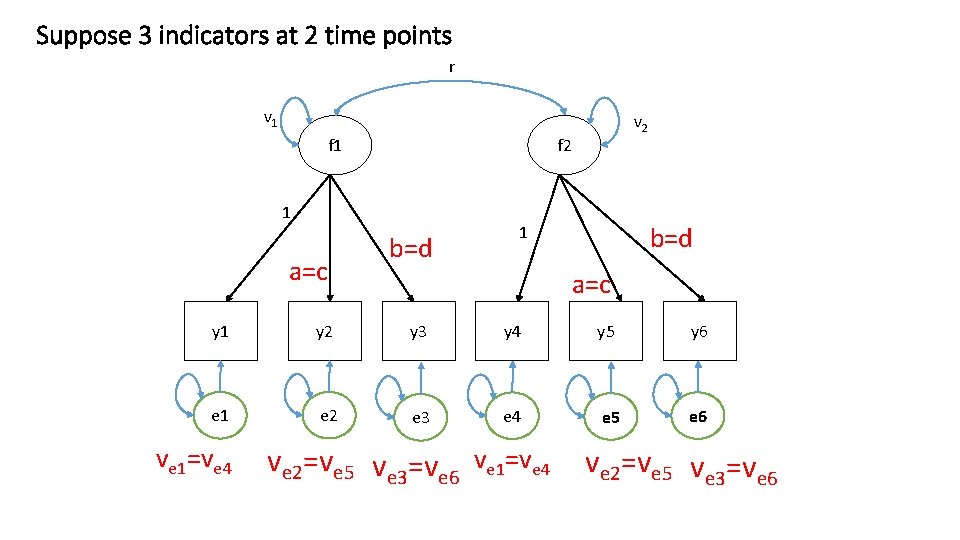
Suppose 3 indicators at 2 time points r v 1 f 2 1 1 b d a y 1 ve 1 y 2 e 1 c y 3 e 2 y 4 ve 14 ve 3 ve 2 v 2 e 3 y 5 ve 6 ve 5 e 4 y 6 e 5 e 6

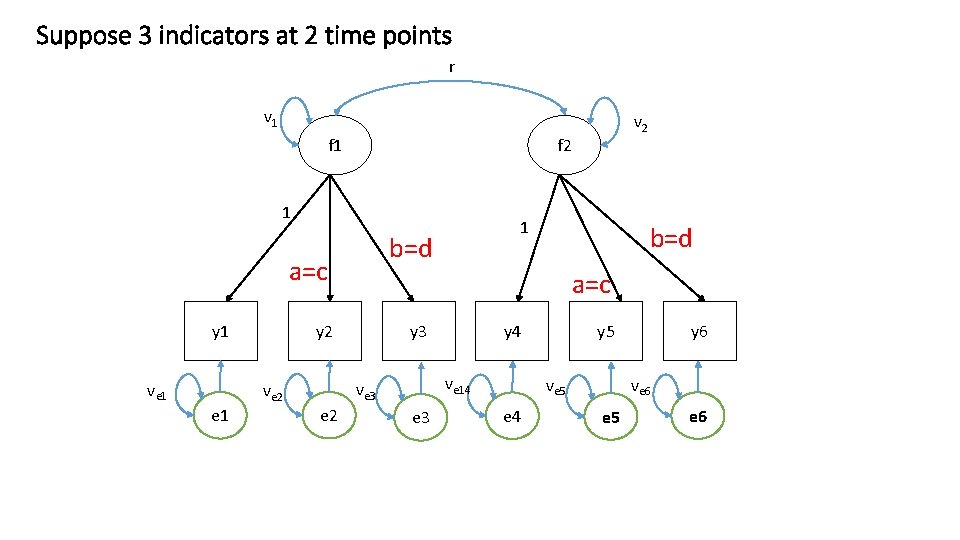
Suppose 3 indicators at 2 time points r v 1 f 2 1 ve 1 y 3 y 4 ve 14 ve 3 e 2 b=d a=c y 2 ve 2 1 b=d a=c y 1 v 2 e 3 y 5 ve 6 ve 5 e 4 y 6 e 5 e 6

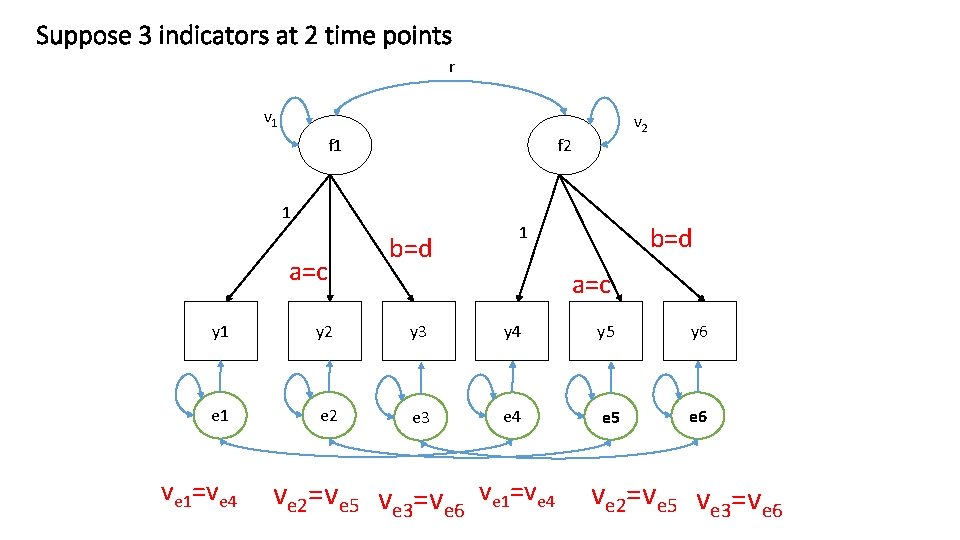
Suppose 3 indicators at 2 time points r v 1 f 2 1 a=c v 2 b=d 1 a=c y 1 y 2 y 3 y 4 y 5 y 6 e 1 e 2 e 3 e 4 e 5 e 6 ve 1=ve 4 ve 2=ve 5 ve 3=ve 6

Suppose 3 indicators at 2 time points r v 1 f 2 1 a=c v 2 b=d 1 a=c y 1 y 2 y 3 y 4 y 5 y 6 e 1 e 2 e 3 e 4 e 5 e 6 ve 1=ve 4 ve 2=ve 5 ve 3=ve 6

MZ=DZ=1 1 E A C e c a 1 MZ=1 / DZ=. 5 1 1 A E C a T 1 c e T 2 Equality constraints are nothing new!

The linear common factor model: “continuous” indicators (7 point Likert scale is “continuous”) What about ordinal or binary indicators? Linear regression model is key ingredient in the linear factor model Logistic or probit regression is a key ingredient in ordinal or discrete factor analysis.
![The model for the Yi b 0 b 1Xi ei EYXx The model for the Yi = b 0 + b 1*Xi + ei E[Y|X=x˚]](https://slidetodoc.com/presentation_image_h/36b3c9e36cc32442be9117399f8b10ad/image-49.jpg)
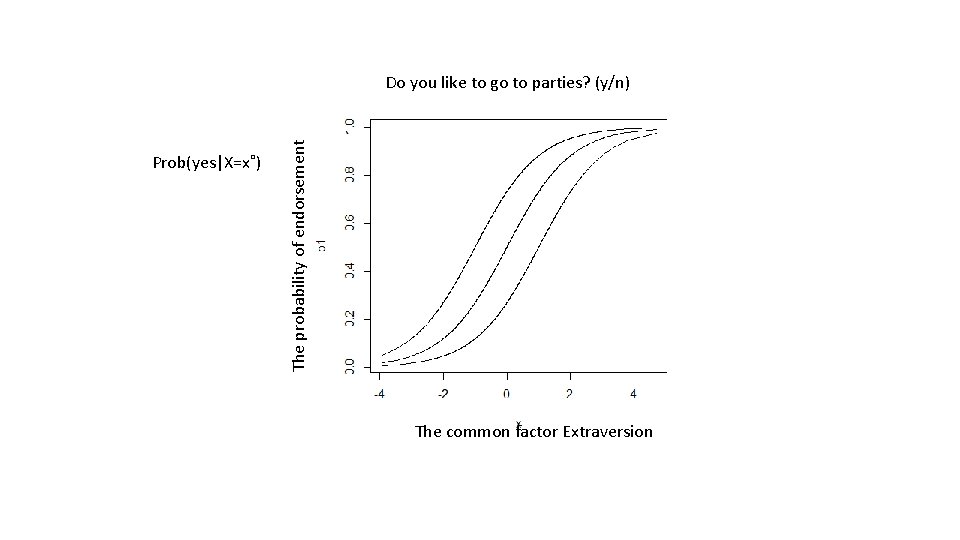
The model for the Yi = b 0 + b 1*Xi + ei E[Y|X=x˚] = b 0 + b 1*x˚ Logit: E[Z|X=x˚] = Prob(Z=0|X=x˚) = exp(b 0 + b 1*x˚) / {1 + exp(b 0 + b 1*x˚)} Probit: E[Z|X=x˚] = Prob(Z=0|X=x˚) = F(b 0 + b 1*x˚), F(. ) cumulative st. normal distribution Replace X, observed predictor, but , the common factor.

Prob(yes|X=x˚) The probability of endorsement Do you like to go to parties? (y/n) The common factor Extraversion
 Neale donald walsch pensées quotidiennes
Neale donald walsch pensées quotidiennes Zora neale hurston mother
Zora neale hurston mother Zora neale hurston
Zora neale hurston John neale elizabeth i
John neale elizabeth i John hottinger fairfield university
John hottinger fairfield university Wide isa vs narrow isa
Wide isa vs narrow isa Conor doherty model
Conor doherty model Conor cashman
Conor cashman Institution politique
Institution politique Conor mcguckin
Conor mcguckin Conor harris biomechanics
Conor harris biomechanics Matthew dolan attorney
Matthew dolan attorney Dolan hall fairfield university
Dolan hall fairfield university Yvonne dolan
Yvonne dolan Statistics sample rates conor cunningham
Statistics sample rates conor cunningham Icp 17
Icp 17 Cushing dolan
Cushing dolan Conor morley
Conor morley Natalie dolan
Natalie dolan Conor bulman
Conor bulman Conor mayo-wilson
Conor mayo-wilson Cushing dolan
Cushing dolan Conor walsh harvard
Conor walsh harvard Trihybrid heterozygous cross
Trihybrid heterozygous cross Punnett square
Punnett square Phenotypic characteristics of bacteria
Phenotypic characteristics of bacteria Phenotypic ratio of dihybrid cross
Phenotypic ratio of dihybrid cross Phenotypic characteristics of bacteria
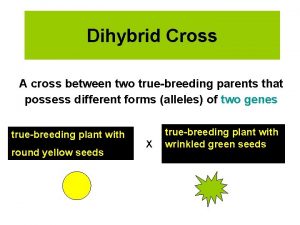
Phenotypic characteristics of bacteria Dihybrid cross of round yellow and wrinkled green
Dihybrid cross of round yellow and wrinkled green Parent offspring regression
Parent offspring regression Phenotypic mixing
Phenotypic mixing Genotype vs phenotype ratio
Genotype vs phenotype ratio Incomplete penetrance
Incomplete penetrance What is the genotypic and phenotypic ratio
What is the genotypic and phenotypic ratio Gutsy
Gutsy Genotype
Genotype Who is the father of genetics
Who is the father of genetics Genotype ratio
Genotype ratio Difference between factor analysis and cluster analysis
Difference between factor analysis and cluster analysis 8-2 factoring by gcf
8-2 factoring by gcf Factoring greatest common factor
Factoring greatest common factor Power of sine wave
Power of sine wave Situation-relating questions examples
Situation-relating questions examples Factoring greatest common factor
Factoring greatest common factor Factors 0f 18
Factors 0f 18 Biografia michel de montaigne
Biografia michel de montaigne Mondini deformitesi
Mondini deformitesi Foucault poststructuralism
Foucault poststructuralism Programmation lineaire
Programmation lineaire Michel lodolo
Michel lodolo Michel grangeat
Michel grangeat