OPTIMISATION 1re anne ingnieurs rachid chelouaheisti fr OPTIMISATION

OPTIMISATION 1ère année ingénieurs rachid. chelouah@eisti. fr

OPTIMISATION § § § Concepts de base: recherche opérationnelle Programmation linéaire Méthode du simplexe Logiciels (Scilab, Solveur Excel, Solveur SAS, LINDO, Eclipse) Variables artificielles et pénalités üMéthode du grand M üMéthode des 2 phases § § Dualité Programmation en nombres entiers Programmation en nombres binaires Heuristiques ü Algorithmes génétiques ü Algorithme de colonie de fourmis ü Algorithme de recherche tabou

Chapitre 0. Concepts de base : recherche opérationnelle

DEFINITIONS § Application de méthodes, techniques, instruments scientifiques pour modéliser et résoudre les problèmes dans tous les domaines § Application de la méthode scientifique pour modéliser et résoudre les problèmes dans tous les domaines

ORIGINES § Développement durant la seconde guerre mondiale • applications aux opérations militaires § § répartition des troupes, du matériel, des ressources approvisionnement en vivres, en pièces, en armement § Scientifiques et ingénieurs: applications civiles • programmation linéaire (1ère publication en 1939) • développement du simplexe par G. Dantzig (1947) • développement des techniques classiques en programmation linéaire, non-linéaire, dynamique, théorie des files d’attente, etc. • ralentissement des recherches généré par le manque d’outils de calcul

APPLICATIONS § Applications aux problèmes réels de grande envergure • arrivée des processeurs rapides • développement des bases de données • techniques d ’optimisation appliquées à de nombreux domaines § Domaines d’utilisation • militaire • transport (aériens, routiers et ferroviaires ) § route, trajet, livraison § horaire • contrôle des réseaux § infrastructures, distribution § télécommunications, • industrie forestière, • énergie (pétrole, gaz, électricité, nucléaire), • Finance, • etc.

METHODES § § § Techniques mathématiques Techniques statistiques Modèles de gestion des stocks Modèles d’affectation Modèles de programmation dynamique Modèles de files d’attente Modèles séquentiels Modèles de remplacement Modèles de compétition Techniques de simulation Méthodes heuristiques

MODELES MATHEMATIQUES § Modèles déterministes • Incertitude négligeable • Résultats du phénomène prévu avec certitude § Modèles probabilistes ou stochastiques • Incertitude considérée comme facteur important du phénomène ou système analysé

FORMULATION DU MODELE MATHEMATIQUE § Définir le problème • • Quelle est la nature exacte du problème? Quel est l’objectif recherché? Quelles sont les conditions d’opération? Quels sont les paramètres à considérer? Quelle influence? • Quel est le degré de précision requis?

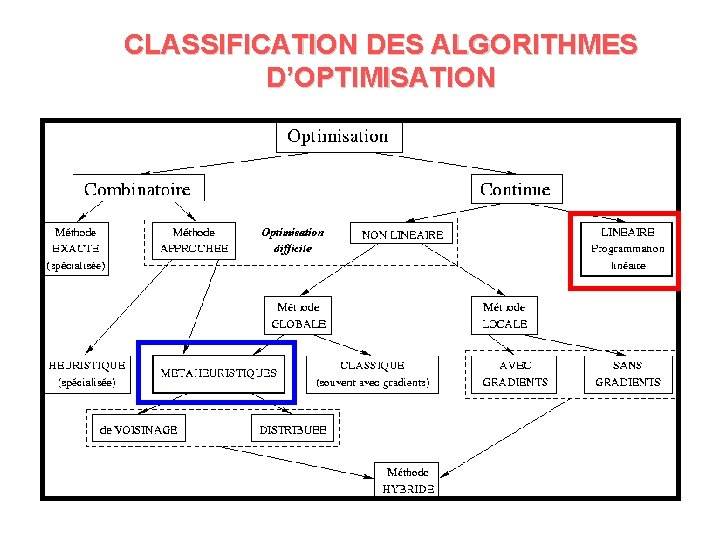
CLASSIFICATION DES ALGORITHMES D’OPTIMISATION

Chapitre 1. Programmation linéaire

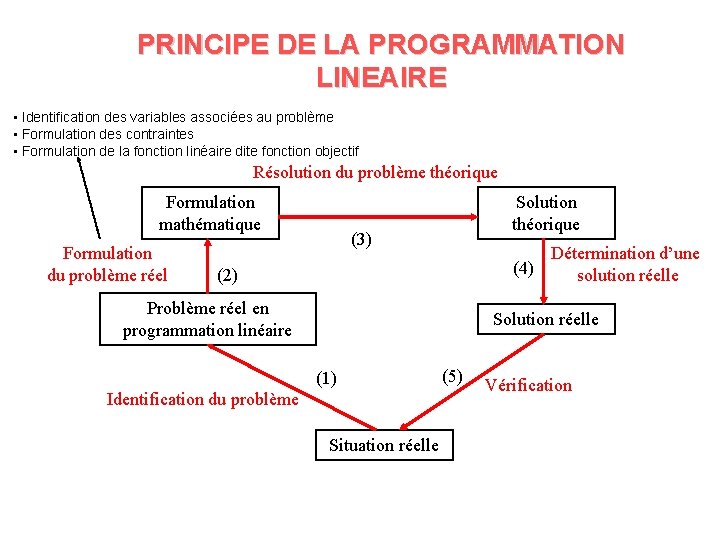
PRINCIPE DE LA PROGRAMMATION LINEAIRE • Identification des variables associées au problème • Formulation des contraintes • Formulation de la fonction linéaire dite fonction objectif Résolution du problème théorique Formulation mathématique Formulation du problème réel Solution théorique (3) Détermination d’une (4) solution réelle (2) Problème réel en programmation linéaire Solution réelle (1) Identification du problème Situation réelle (5) Vérification

PROGRAMME LINÉAIRE § Programmation linéaire • problème d’optimisation consistant à maximiser (ou minimiser) une fonction objectif linéaire de n variables de décision soumises à un ensemble de contraintes exprimées sous forme d’équations ou d’inéquations linéaires § Différentes programmations linéaires • • Programmation Linéaire classique Programmation Linéaire en Nombre Entiers Programmation Linéaire en 0 -1 Programmation Linéaire Mixte § La terminologie est due à George B. Dantzig, inventeur de l’algorithme du simplexe (1947)

MISE EN FORME MATHÉMATIQUE § Définir les variables de décision • ensemble des variables qui régissent la situation à modéliser • variables réelles, entières, binaires § Préciser la fonction objectif • fonction mathématique composée des variables de décision qui représente le modèle physique modélisé • fonction linéaire, non-linéaire § Préciser les contraintes du problème • ensemble des paramètres qui limitent le modèle réalisable • équations ou inéquations composées des variables de décision § Préciser les paramètres du modèle • constantes associées aux contraintes et à la fonction objective

MODELE LINEAIRE § Exemple : 3 types de machines A, B et C pour produire 4 produits différents I, III et IV. Chaque produit doit être traité par chacune des machines dans l’ordre

MODELE LINEAIRE § Exemple : Caractéristiques des produits & machines Type de machine Produits Disponibilité hebdomadaire de chaque machines I II IV 1 2, 4 1 2000 B 1, 5 1 3, 5 8000 C 1, 5 3 3, 5 1 5000 5, 24 7, 30 8, 34 4, 18 A Profit par unité

MODELE LINEAIRE § Exemple : • But : établir la production hebdomadaire de chaque produit de façon à maximiser le profit. § Le modèle : xj - production hebdomadaire du produit j. but : trouver les valeurs de x 1 , x 2 , x 3 et x 4 qui maximisent le profit, considérant la limite de temps d’utilisation de chaque machine

MODELE LINEAIRE § Exemple : • But : max z = 5, 24 x 1 + 7, 30 x 2 + 8, 34 x 3 + 4, 18 x 4 • Contraintes des machines : A : 1, 5 x 1 + x 2 + 2, 4 x 3 + x 4 B : x 1 + 5 x 2 + x 3 + 3, 5 x 4 C : 1, 5 x 1 + 3 x 2 + 3, 5 x 3 + x 4 • Contraintes de non négativité : x 1 , x 2 , x 3 , x 4 0 2000 8000 5000

PROGRAMMATION LINÉAIRE § Validation du modèle et des résultats • S’assurer § § que le modèle développé est conforme à la réalité que les résultats sont valides dans toutes les conditions § Conception du système d’application • Possibilité d’utiliser des logiciels spécialisés § Implantation

FORMULATION MATHÉMATIQUE D’UN PROGRAMME LINÉAIRE § FONCTION OBJECTIF (f. o. ) • Maximiser ou minimiser • z = c 1 x 1 + c 2 x 2 + c 3 x 3 + … + + cnxn § Contraintes • a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 nxn ( , =, ) b 1 • a 21 x 1 + a 22 x 2 + a 23 x 3 + … + a 2 nxn ( , =, ) b 2 • am 1 x 1 + am 2 x 2 + am 3 x 3 + … + amnxn ( , =, ) bm § Contraintes de non-négativité • xj 0 ; j = 1, 2, 3, … n § avec • xj • aij, bi, cj variables de décision (inconnues) paramètres du programme linéaire

TERMINOLOGIE DE LA SOLUTION § Solution réalisable • Solution où toutes les contraintes du modèle sont satisfaites § Zone de solutions • Ensemble de toutes les solutions réalisables § Solution optimale • Solution réalisable où la fonction objectif atteint la meilleure valeur, maximum ou minimum • Plusieurs solutions optimales possibles

RESOLUTION GRAPHIQUE § Problème à deux variables de décision x 1 et x 2 : • f. o. - droite dans 2 • contraintes - hemi-plans de 2 • P = (x 1 , x 2 ) - solution admissible (réalisable) si P satisfait toutes les contraintes • région admissible - l’ensemble des solutions admissibles • solution optimale - solution admissible qui optimise la f. o.

PROGRAMMATION LINÉAIRE § Résolution selon les techniques appropriées • Exemple § § MAXIMISER z = 3 x 1 + 5 x 2 SUJET À • • x 1 4 2 x 2 12 3 x 1 + 2 x 2 18 x 1 0 ; x 2 0 • Solutions optimales § § § programmation linéaire: simplexe programmation en nombre entier: branch-and-bound programmation dynamique • Solutions sous-optimales: heuristiques

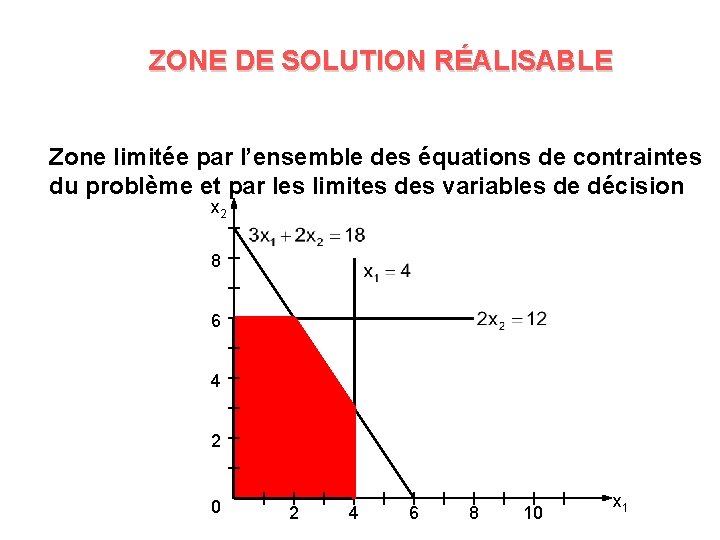
ZONE DE SOLUTION RÉALISABLE Zone limitée par l’ensemble des équations de contraintes du problème et par les limites des variables de décision x 2 8 6 4 2 0 2 4 6 8 10 x 1

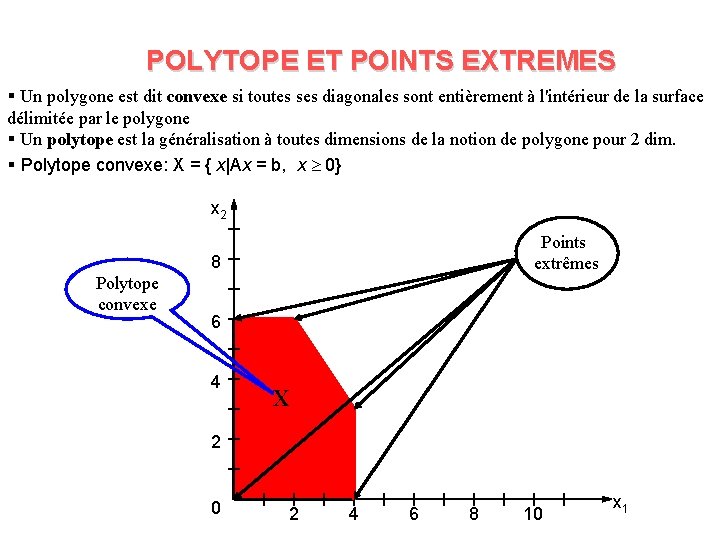
POLYTOPE ET POINTS EXTREMES § Un polygone est dit convexe si toutes ses diagonales sont entièrement à l'intérieur de la surface délimitée par le polygone § Un polytope est la généralisation à toutes dimensions de la notion de polygone pour 2 dim. § Polytope convexe: X = { x|Ax = b, x 0} x 2 Points extrêmes 8 Polytope convexe 6 4 X 2 0 2 4 6 8 10 x 1

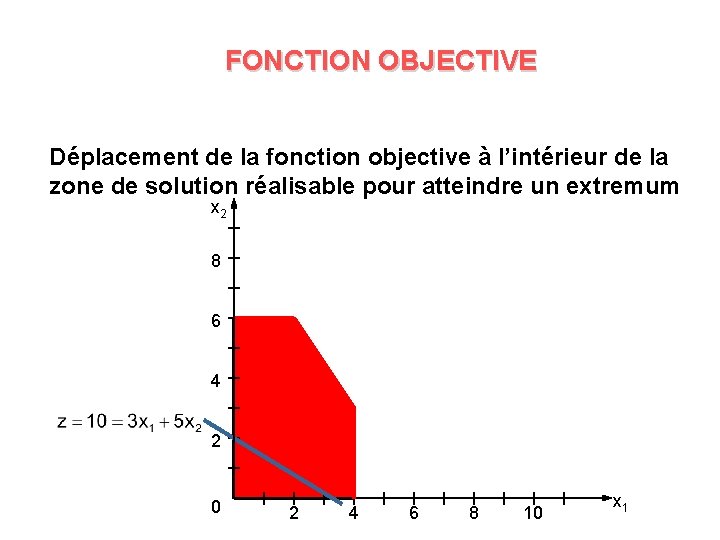
FONCTION OBJECTIVE Déplacement de la fonction objective à l’intérieur de la zone de solution réalisable pour atteindre un extremum x 2 8 6 4 2 0 2 4 6 8 10 x 1

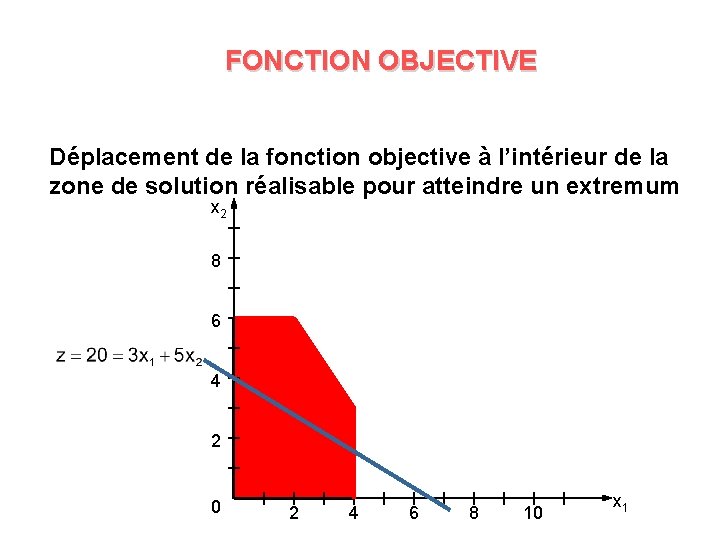
FONCTION OBJECTIVE Déplacement de la fonction objective à l’intérieur de la zone de solution réalisable pour atteindre un extremum x 2 8 6 4 2 0 2 4 6 8 10 x 1

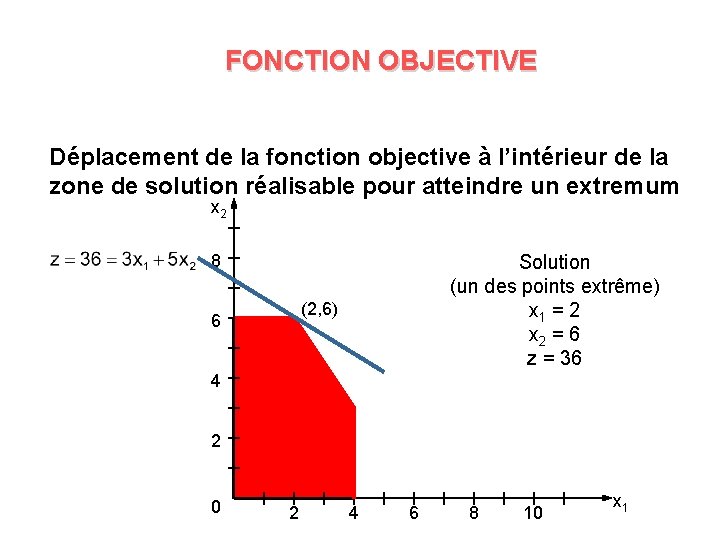
FONCTION OBJECTIVE Déplacement de la fonction objective à l’intérieur de la zone de solution réalisable pour atteindre un extremum x 2 8 Solution (un des points extrême) x 1 = 2 x 2 = 6 z = 36 (2, 6) 6 4 2 0 2 4 6 8 10 x 1

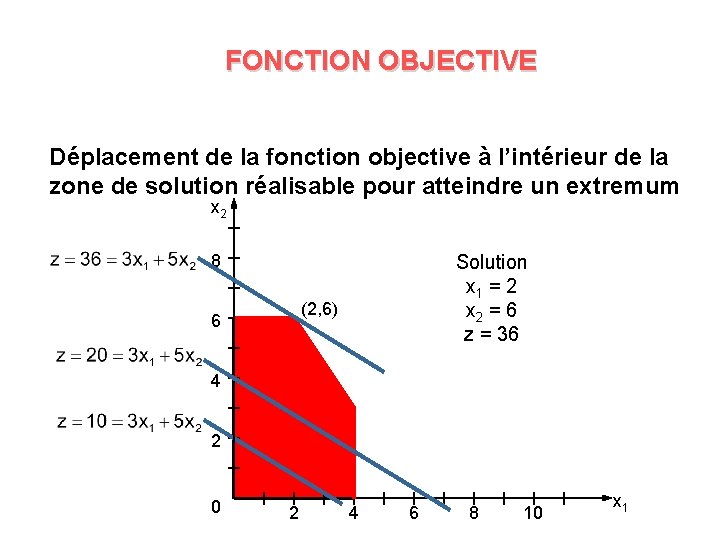
FONCTION OBJECTIVE Déplacement de la fonction objective à l’intérieur de la zone de solution réalisable pour atteindre un extremum x 2 8 Solution x 1 = 2 x 2 = 6 z = 36 (2, 6) 6 4 2 0 2 4 6 8 10 x 1

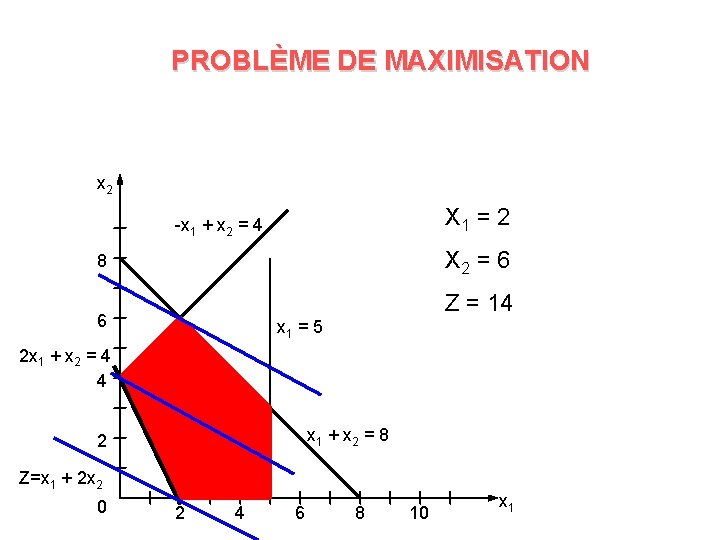
PROBLÈME DE MAXIMISATION § Maximiser Z = x 1 + 2 x 2 Sujet à 2 x 1 + x 2 4 x 1 + x 2 8 -x 1 + x 2 4 x 1 5 x 1 0, x 2 0

PROBLÈME DE MAXIMISATION x 2 X 1 = 2 -x 1 + x 2 = 4 X 2 = 6 8 Z = 14 6 x 1 = 5 2 x 1 + x 2 = 4 4 x 1 + x 2 = 8 2 Z=x 1 + 2 x 2 0 2 4 6 8 10 x 1

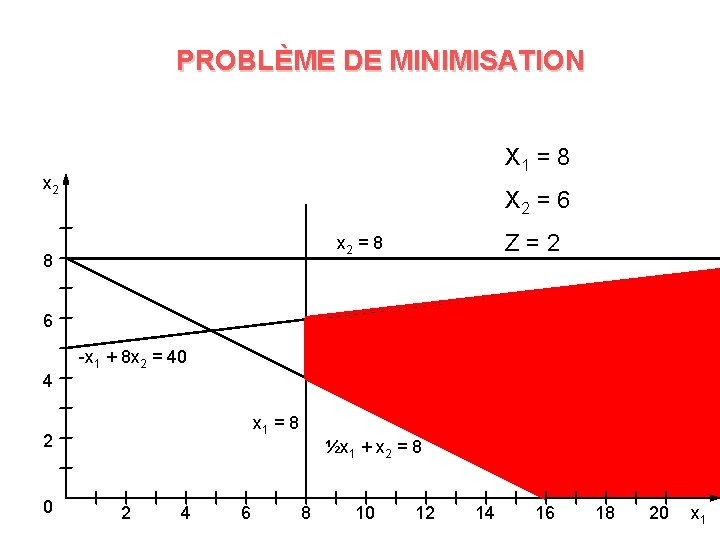
PROBLÈME DE MINIMISATION § Minimiser Z = x 1 - x 2 Sujet à ½x 1 + x 2 8 -x 1 + 8 x 2 40 x 1 8 x 2 8 x 1 0, x 2 0

PROBLÈME DE MINIMISATION X 1 = 8 x 2 X 2 = 6 Z = 2 x 2 = 8 8 6 -x 1 + 8 x 2 = 40 4 x 1 = 8 2 0 ½x 1 + x 2 = 8 2 4 6 8 10 12 14 16 18 20 x 1

RÉSULTAT D’UNE OPTIMISATION LINÉAIRE Le domaine admissible d’un PL peut être • vide: dans un tel cas, le problème est sans solution admissible (pas de solution optimale) • borné (et non vide): le problème possède toujours au moins une solution optimale • non borné: dans ce cas, selon la fonction objectif § § § le problème peut posséder des solutions optimales il peut exister des solutions admissibles de valeur arbitrairement grande (ou petite) dans un tel cas, le PL n'admet pas de solution optimale finie et est dit non borné

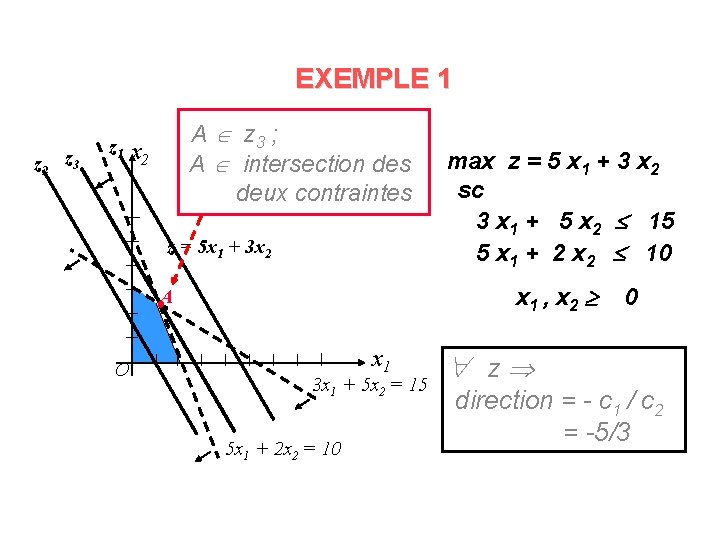
EXEMPLE 1 x 2 max z = 5 x 1 + 3 x 2 sc 3 x 1 + 5 x 2 15 5 x 1 + 2 x 2 10 x 1 , x 2 O x 1 3 x 1 + 5 x 2 = 15 5 x 1 + 2 x 2 = 10 0

EXEMPLE 1 z 2 z 3 z 1 A z 3 ; A intersection des deux contraintes x 2 z = 5 x 1 + 3 x 2 x 1 , x 2 A O max z = 5 x 1 + 3 x 2 sc 3 x 1 + 5 x 2 15 5 x 1 + 2 x 2 10 x 1 3 x 1 + 5 x 2 = 15 5 x 1 + 2 x 2 = 10 0 z direction = - c 1 / c 2 = -5/3

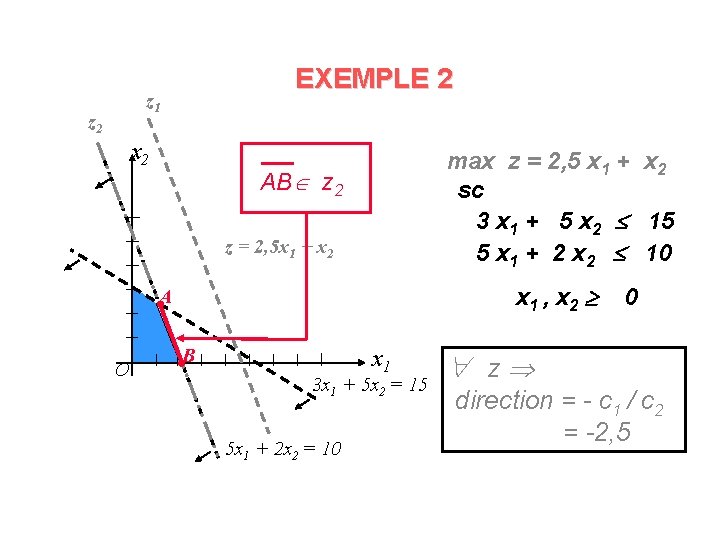
EXEMPLE 2 z 1 z 2 x 2 max z = 2, 5 x 1 + x 2 sc 3 x 1 + 5 x 2 15 5 x 1 + 2 x 2 10 AB z 2 z = 2, 5 x 1 + x 2 x 1 , x 2 A O B x 1 3 x 1 + 5 x 2 = 15 5 x 1 + 2 x 2 = 10 0 z direction = - c 1 / c 2 = -2, 5

RESUME § Région admissible borné : • polygone dont les côtés sont des segments des droites représentant les contraintes linéaires du problème • un point P à l ’intersection de 2 côtés du polygone est un point extrême • solution optimale: § § point extrême solution optimale unique côté du polygone infinité de solutions optimales ( la valeur de la f. o. est unique )

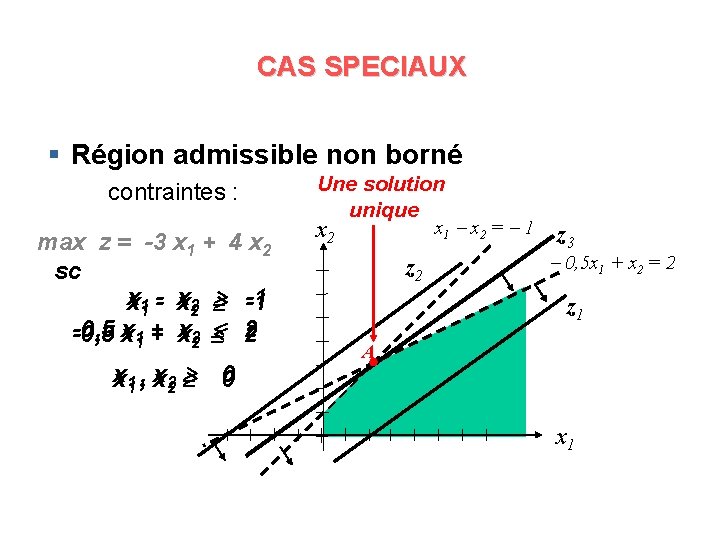
CAS SPECIAUX § Région admissible non borné contraintes : max z = -3 x 1 + 4 x 2 sc x x 11 -- x x 22 -1 -1 -0, 5 x x 11 + + x x 22 2 2 x x 11 , , x x 22 0 0 Une solution unique x 1 x 2 = 1 x 2 z 3 0, 5 x 1 + x 2 = 2 z 1 A x 1

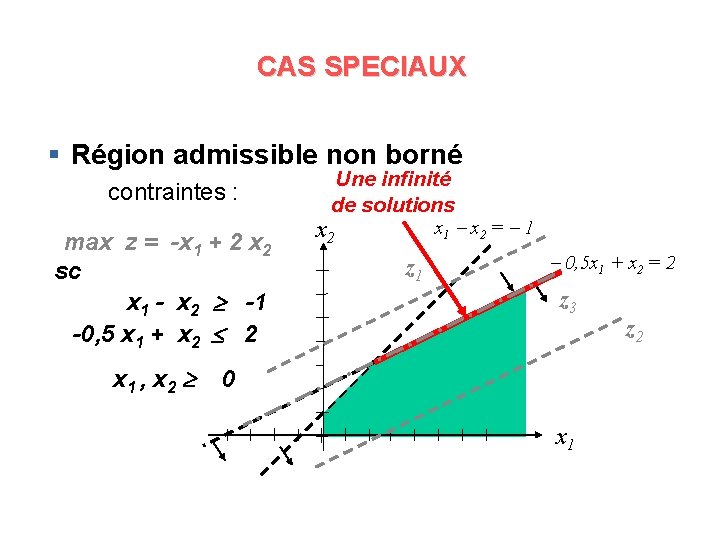
CAS SPECIAUX § Région admissible non borné contraintes : max z = -x 1 + 2 x 2 sc x 1 - x 2 -1 -0, 5 x 1 + x 2 2 x 1 , x 2 Une infinité de solutions x 1 x 2 = 1 x 2 z 1 0, 5 x 1 + x 2 = 2 z 3 0 x 1 z 2

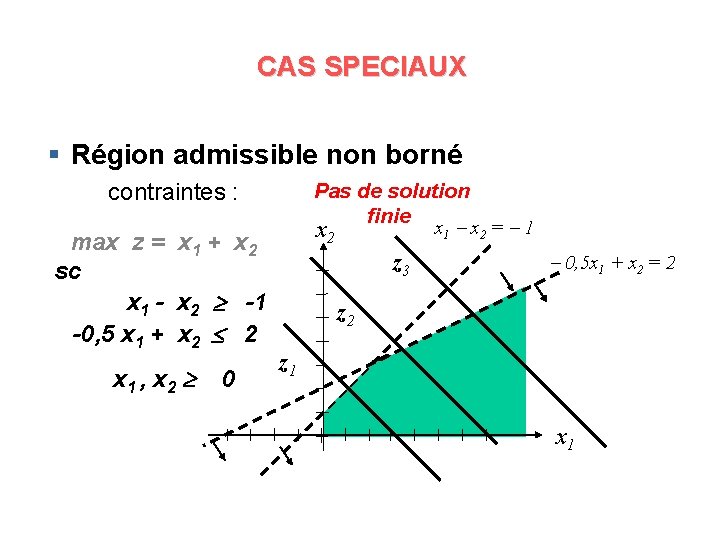
CAS SPECIAUX § Région admissible non borné contraintes : max z = x 1 + x 2 sc x 1 - x 2 -1 -0, 5 x 1 + x 2 2 x 1 , x 2 0 Pas de solution finie x 1 x 2 = 1 x 2 z 3 0, 5 x 1 + x 2 = 2 z 1 x 1

RESUME § Région admissible non borné : • solution optimale: § point extrême solution optimale unique § côté de la région admissible infinité de solutions optimales ( la valeur de la f. o. est unique ) § pas de solution optimale finie

UN DERNIER CAS SPECIAL § Région admissible vide contraintes incompatibles 1 x 2 2 x 1 + 3 x 2 = 6 x 1 + x 2 = 5 x 1 x 2 = 1 x 1 er cas : des hemi plans est vide x 1 + x 2 5 - 2 x 1 + 3 x 2 6 x 1 - x 2 1 x 1 , x 2 0

UN DERNIER CAS SPECIAL § Région admissible vide contraintes incompatibles x 2 x 1 + x 2 = 1 x 1 + x 2 = 1 ème 2 cas : contrainte de non négativité pas satisfaite x 1 + x 2 -1 x 1 - x 1 + x 2 1 x 1 , x 2 0

CONCLUSION Pour chaque problème PL : • Solution optimale unique • Infinité de solutions optimales • Solution optimale infinie • Aucune solution

GENERALISATION § Problème à r > 2 variables de décision solution graphique ? !? ! § Vocabulaire suggéré par la méthode graphique : 1 - région admissible : région convexe d’un espace de dimension r ( polyèdre convexe ) 2 - un point P à l’intersection de s 2 hyperplans représentant les contraintes est un point extrême du polyèdre

GENERALISATION § Problème à r > 2 variables de décision solution graphique ? !? ! § Vocabulaire suggéré par la méthode graphique : 3 - solution optimale: § § unique point extrême du polyèdre infinité de solutions optimales frontière du polyèdre = hyperplan de dimension < r ( la valeur de la f. o. est unique )

METHODE DU SIMPLEXE § Méthode exacte et itérative § Parcours des points extrêmes jusqu’à trouver la (les) solution(s) optimale(s), si en existe § Identification des cas de contraintes incompatibles § Basée sur l’algèbre des matrices