OPTIMISATION 1re anne ingnieurs rachid chelouaheisti fr OPTIMISATION

OPTIMISATION 1ère année ingénieurs rachid. chelouah@eisti. fr

OPTIMISATION § § § Concepts de base: recherche opérationnelle Programmation linéaire Méthode du simplexe Logiciels (Scilab, Solveur Excel, Solveur SAS, LINDO, Eclipse) Variables artificielles et pénalités 1. Méthode du grand M üMéthode des 2 phases § § Dualité Programmation en nombres entiers Programmation en nombres binaires Heuristiques ü Algorithmes génétiques ü Algorithme de colonie de fourmis ü Algorithme de recherche tabou

INTRODUCTION § développée initialement par George Dantzig en 1947 § seule méthode exacte pour solutionner des problèmes linéaires de grande taille § méthode itérative algébrique où l’on circule séquentiellement sur les sommets à l’intérieur de la zone de solution jusqu’à l’obtention de la solution optimale

PROPRIÉTÉS DU SIMPLEXE § Zone de solution du problème linéaire toujours convexe § S’il existe une seule solution optimale au problème linéaire, elle est obligatoirement localisée sur un sommet de la zone de solution § S’il existe de multiples solutions optimales, au moins deux d’entre elles doivent être localisées sur des sommets adjacents § Le nombre de sommets de la zone de solution est fini § Si la solution réalisable localisée à un sommet donné n’a pas de voisin adjacent dont la solution est supérieure, ce sommet est la solution optimale

FORME CANONIQUE § PROBLÈME DE MAXIMISATION § PROBLÈME DE MINIMISATION

FORME NORMALISÉE § PROBLÈME DE MAXIMISATION § PROBLÈME DE MINIMISATION

Variables de base et variables hors base Le passage de la forme canonique à la forme normalisée en introduisant des variables d’écart (variables supplémentaires) Variables de base : variables supplémentaires + la variable Z Variables hors base : variables xi du système initial

MÉTHODE DU SIMPLEXE DÉFINITIONS § Systèmes d’équations équivalents • Systèmes qui possèdent le même ensemble de solutions § Variable de base • Variable qui a un coefficient unitaire positif dans une des équations du système et un coefficient nul partout ailleurs § Opérations pivot • Opération de Gauss-Jordan pour transformer un système d’équations équivalent dans lequel une variable devient de base § Système canonique • Système d’équations où il y a une variable de base par équation § Solution de base • Système d’équations où les variables hors base sont fixées à zéro résolu pour les variables de base

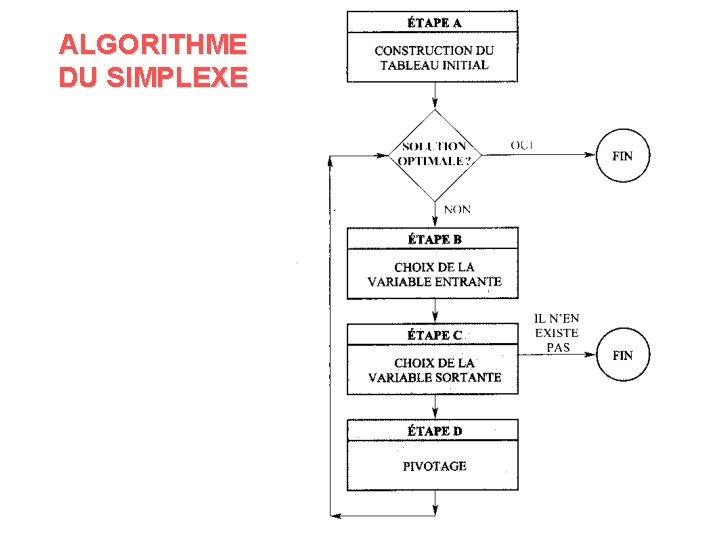
ALGORITHME DU SIMPLEXE 1. Déterminer une solution de base (sommet du polytope) réalisable (vérifiant toutes les contraintes) 2. Vérifier si la solution actuelle est optimale 3. Déterminer la variable hors base qui va devenir variable de base (accroissement de la fonction objectif) 4. Déterminer la variable de base qui sortira de la solution 5. Effectuer les opérations linéaires (pivots) selon la technique de Gauss-Jordan 6. Répéter (tant que c’est possible)

ALGORITHME DU SIMPLEXE

MÉTHODE DU SIMPLEXE § FORME CANONIQUE Max Z = 3 x 1 + 5 x 2 sujet à x 1 4 2 x 2 12 3 x 1 + 2 x 2 18 et x 1 0, x 2 0

MÉTHODE DU SIMPLEXE § FORME NORMALISÉE Max Z Z - 3 x 1 - 5 x 2 x 1 + x 3 2 x 2 + x 4 = 12 3 x 1 + 2 x 2 + x 5 = 18 avec xj 0, pour j =1, 2, 3, 4, 5 = 0 = 4 (2) (3) (0) (1)

MÉTHODE DU SIMPLEXE § ÉTAPE D’INITIALISATION • • Déterminer une solution de base réalisable Porter les variables hors base à zéro Solutionner les variables de base Exemple: § § z, x 3, x 4 et x 5 sont les variables de base x 1 et x 2 sont les variables hors base • On obtient: § § § x 1 = 0 et x 2 = 0 x 3 = 4, x 4 = 12 et x 5 = 18 z=0

MÉTHODE DU SIMPLEXE § VARIABLE ENTRANT DANS LA BASE • Variable hors base entrant dans la base • Celle qui sera choisie fera augmenter la valeur de la fonction objective le plus rapidement possible • Variable ayant le plus grand coefficient négatif (cas de maximisation) de l’équation (0) • Exemple: § X 2 devient variable de base

MÉTHODE DU SIMPLEXE § VARIABLE SORTANT DE LA BASE • Variable qui limitera le plus rapidement la progression de la nouvelle variable de base • Exemple § § si x 2 entre dans la base équation (2) • • § équation (3) • • § 2 x 2 + x 4 = 12 x 2 max = 6 3 x 1 + 2 x 2 + x 5 = 18 x 2 max = 9 limite maximale de x 2 égale 6 sinon x 4 devient négatif

MÉTHODE DU SIMPLEXE § OPÉRATIONS PIVOT • Système d’équations original (variables de base en gras) Z - 3 x 1 - 5 x 2 2 x 2 + x 3 + x 4 + x 5 = 0 = 4 = 12 = 18 (0) (1) (2) (3) • Pour revenir à la forme canonique, il faut que les variables de base aient un coefficient unitaire dans une équation et nul dans les autres • Équation (2) multipliée par ½ 2 x 2/2 x 2 + x 4/2 = 12 /2 (2) + ½ x 4= 6 (2) • Il faut éliminer les termes x 2 des autres équations

MÉTHODE DU SIMPLEXE § OPÉRATIONS PIVOT (suite) • Équation (0) = ancienne (0) + 5 équation (2) Z Z - 3 x 1 - 5 x 2 - 3 x 1 + 5/2 x 4 = 30 + 5/2 x 4 = 0 (2) = 30 (0) • Équation (3) = ancienne (3) – 2 équation (2) 3 x 1 + 2 x 2 - 2 x 2 + x 5 - x 4 + x 5 = 18 = -12 =6 (3) (2) (3)

MÉTHODE DU SIMPLEXE § OPÉRATIONS PIVOT (suite) • Nouveau système équivalent d’équations Z - 3 x 1 x 2 + x 3 - 5/2 x 4 = 30 + ½ x 4 - x 4 + x 5 (0) = 4 = 6 (1) (2) (3)

MÉTHODE DU SIMPLEXE § CRITÈRE D’OPTIMALITÉ • Optimalité assurée lorsqu’il est impossible de faire augmenter (cas de maximisation) la valeur de z • Exemple: § § § x 1 peut faire augmenter z Variable entrante x 1 Variable sortante x 5 • équation (1) • • • x 1 + x 3 = 4 x 1 max = 4 équation (3) • • 3 x 1 – x 4 + x 5 = 6 x 1 max = 2

MÉTHODE DU SIMPLEXE § SOLUTION OPTIMALE • Système équivalent d’équations Z x 1 x 2 • Variables hors base § x 4 = 0, x 5 = 0 • Variables de base § x 1 = 2, x 2 = 6, x 3 = 2 • Fonction objective § z = 36 x 3 + 3/2 x 4 + x 5 + 1/3 x 4 - 1/3 x 5 + ½ x 4 - 1/3 x 4 +1/3 x 5 = 36 = 2 = 6 = 2 (0) (1) (2) (3)

SIMPLEXE SOUS FORME TABULAIRE § Méthode essentiellement identique § Informations • Coefficients des variables • Constantes des équations • Variables de base de chaque équation Variables de décision (x 1, x 2)

SIMPLEXE SOUS FORME TABULAIRE § Initialisation § Critère d’optimalité • Coefficients de l’équation (0) non négatifs ? § Itération # 1 • Dans la dernière ligne, on a 2 coefficients négatifs. On prends le plus grands en valeur absolue c’est-à-dire – 5, et on définit la variable entrante • Variable entrante x 2 § Entourer la colonne pivot • Variable sortante x 4 § Entourer la ligne pivot § Point pivot à l’intersection • Transformation de Gauss-Jordan

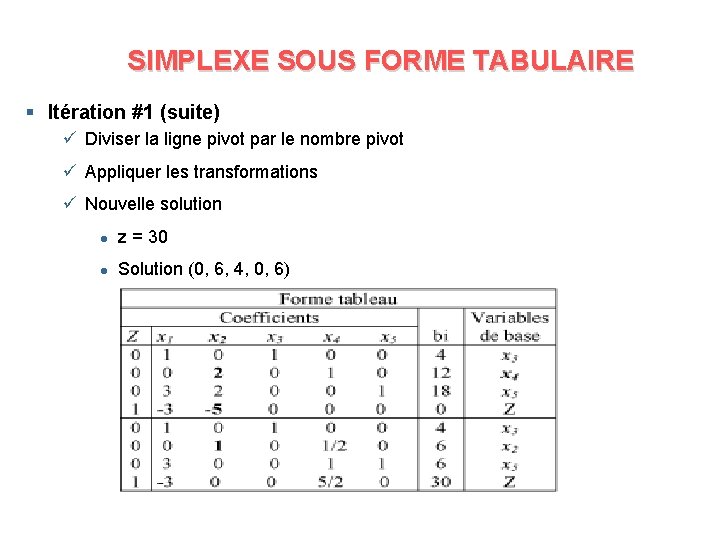
SIMPLEXE SOUS FORME TABULAIRE § Itération #1 (suite) ü Diviser la ligne pivot par le nombre pivot ü Appliquer les transformations ü Nouvelle solution l z = 30 l Solution (0, 6, 4, 0, 6)

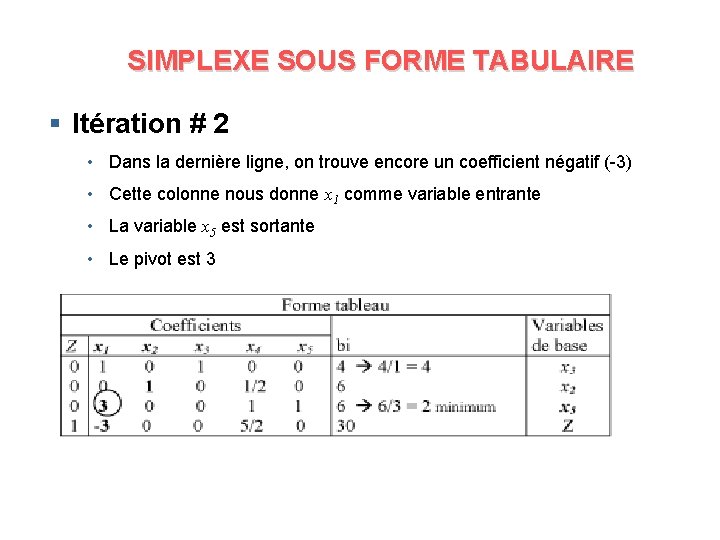
SIMPLEXE SOUS FORME TABULAIRE § Itération # 2 • Dans la dernière ligne, on trouve encore un coefficient négatif (-3) • Cette colonne nous donne x 1 comme variable entrante • La variable x 5 est sortante • Le pivot est 3

SIMPLEXE SOUS FORME TABULAIRE § Ensemble complet § Solution • (2, 6, 2, 0, 0) • z = 36

SITUATIONS PARTICULIÈRES § Égalité des profits relatifs • Choix aléatoire de la variable § Égalité des ratios • Choix aléatoire • Situation de dégénérescence: remonter à l’étape des ratios identiques § Solution non bornée • En pratique, une contrainte est absente § Solutions multiples • Variables hors base avec des coefficients nuls dans la fonction objective § Présence de cyclage • Certaines variables de base sont nulles Règle de Blanc : choisir comme colonne entrante celle de profit marginal positif de plus petit indice

SIMPLEXE SOUS FORME MATRICIELLE § Forme canonique

SIMPLEXE SOUS FORME MATRICIELLE § Forme normalisée

SIMPLEXE SOUS FORME MATRICIELLE § Problème

SIMPLEXE SOUS FORME MATRICIELLE § Itération 0 § X 2 entre § X 4 sort

SIMPLEXE SOUS FORME MATRICIELLE § Itération 1 § X 1 entre § X 5 sort

SIMPLEXE SOUS FORME MATRICIELLE § Itération 2

LOGICIELS

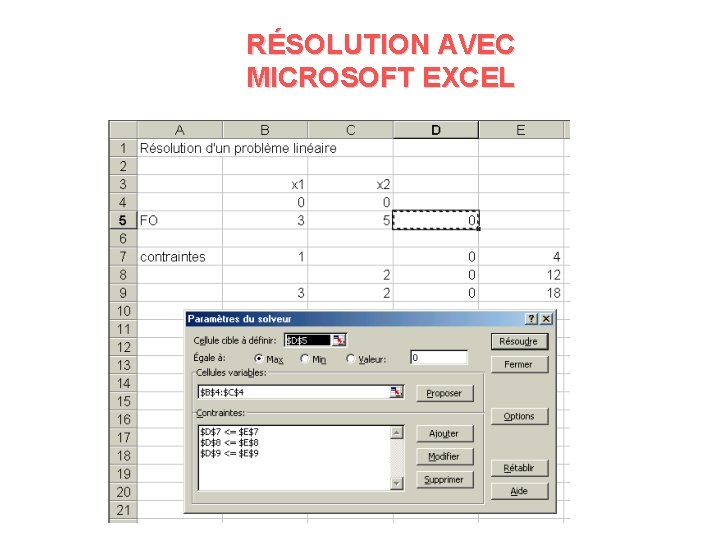
RÉSOLUTION AVEC MICROSOFT EXCEL

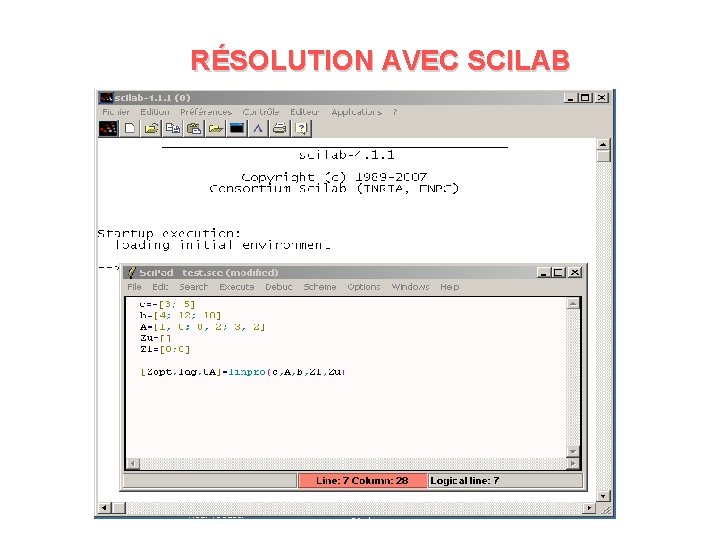
RÉSOLUTION AVEC SCILAB

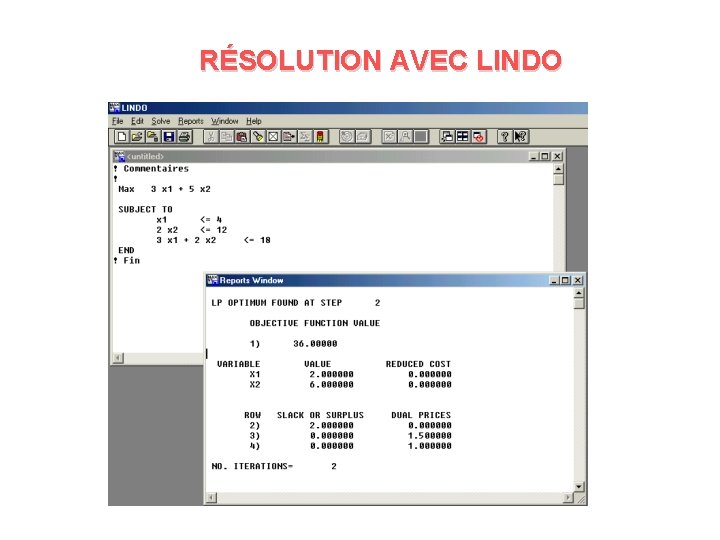
RÉSOLUTION AVEC LINDO