NPcomplete examples CSCI 3130 Tutorial 10 ChunHo Hung

NP-complete examples CSCI 3130 Tutorial 10 Chun-Ho Hung chhung@cse. cuhk. edu. hk Department of Computer Science & Engineering 1

Outline �Review �P, NPC �Polynomial-time Reduction � 2 problems �Double-SAT �Dominating set � http: //en. wikipedia. org/wiki/Dominating_set_problem 2

Review P, NPC Polynomial-time Reduction 3

P �P is the class of all languages that have poly-time algorithm �e. g. , Shortest path on a directed graph, Sorting 4

NP �NP is the class of all languages that have poly-time verifier �A verifier – a Turing Machine, V, s. t. �Given a potential x �x ∈ L V accepts input <x, s> for some s � Solution s �V runs in polynomial time 5

NP (con’t) �While verifying a solution of a NP problem is easy (in poly-time), finding a solution could be more difficult �An 3 SAT instance - Find a satisfying assignment for f = (x 1∨x 2 ) ∧ (x 2 ∨x 3 ∨x 4) ∧ (x 1) �Verifying �Given an assignment, just evaluate the truth value �Finding a solution? �No efficient algorithm has been discovered yet 6

P versus NP �Every language, L in P, L is also in NP �Let Verifier = Poly-time TM that solves L �Therefore �P is contained in NP �Note: L in NP does not imply that efficient algorithm that decides L does not exist NP P 7

NPC �A language C is NP-complete if: �C is in NP �Every language L in NP, L poly-time reduces to C �What is a reduction…? 8

Reduction �The direction of the reduction is very important �Saying “A is easier than B” and “B is easier than A” mean different things �“A (polynomially) reduces to B” means “B is not easier than A” 9

Reduction (Con’t) �Consider 2 problems: 1) BFS on unweighted graph 2) Shortest path on weighted graph �Assume we have a TM, V, which solves 2) �We can reduce 1) to 2): �Given an instance of 1), convert it into an instance of 2): �Copy the graph, add weight=1 to every edge in 2) �Run this instance on V, output result �These two “yes” instances corresponds to each other 10

Poly-Time Reduction �How to show that a problem B is not easier than a problem A? �Informally, if B can be solved efficiently, we can solve A efficiently �Formally, we say A polynomially reduces to B if: 1. Given an instance a of problem, x 2. There is a polynomial time transformation to an instance of B, y = f(x) 3. x is a “yes” instance if and only if y is a “yes” instance 11

Poly-Time Reduction (Con’t) �Suppose A poly-time reduces to B �Then there exists a poly-time TM, R, s. t. , �Given an instance of A, x, transforms it to an instance of B, y = f(x), and �y is accepted x is accepted 12

Poly-Time Reduction (Implication) �Suppose A reduces to B �If B is polynomial time solvable, then A is polynomial time solvable �If A is not polynomial time solvable, then B is not polynomial time solvable �Contrapositive x R Poly-time TM y TM for L’ acc rej 13

Poly-Time Reduction (Implication) �Suppose A reduces to B �Solving B cannot be easier than solving A �Suppose A is “difficult” while B is “easy” �However, by this reduction, you find a “easy” way to solve A �Consequently, if A is NPC, then B must be NPC x R Poly-time TM y TM for L’ acc rej 14

Poly-Time Reduction - P versus NP �To show P = NP, one could try to show that a NPC problem, C, can be solved in polynomial time. Why? �Every problem in NP poly-time reduces to C �If C can be solved in poly-time, so does each problem in NP �Then NP = P!! �But this is not that easy and it is counter-intuitive (to most people) too 15

P versus NP (Again) �Most believe that P ≠ NP, because intuitively searching for a solution is more difficult than verifying a solution �What does P = NP imply? �Know how to verify a solution in poly-time Know how to find a solution in poly-time (? !) �Indeed we prefer P ≠ NP � Encryption ≠ NP algorithms heavily rely on the assumption that P �P = NP or P ≠ NP is still an open problem 16

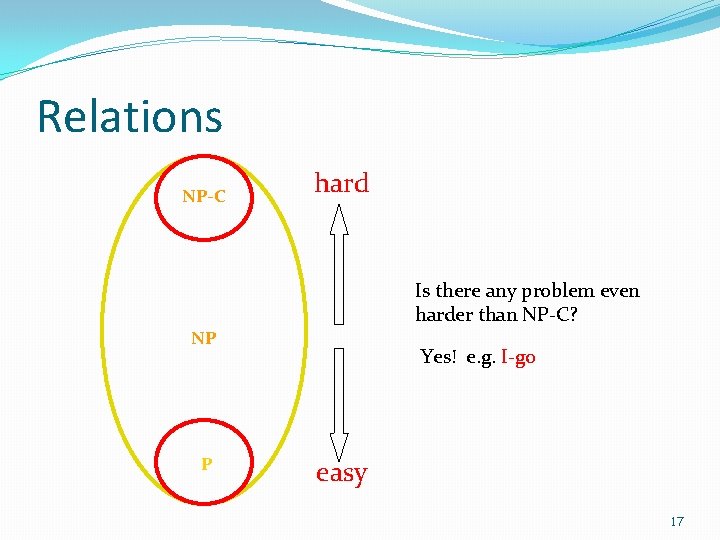
Relations NP-C hard Is there any problem even harder than NP-C? NP P Yes! e. g. I-go easy 17

Methodology �To show L is in NP, you can either (i) Show that solutions for L can be verified in polynomial-time, or (ii) Describe a nondeterministic polynomial-time TM for L (Come back to this if we have enough time) �To show L is NP-complete � Show that L is in NP � Poly-time reduce some NPC problem to L � i. e. , design a polynomial-time reduction from some problem we know to be NPcomplete 18

Example Proving a problem being NPC 19

Double-SAT �Problem: �Double-SAT = {<φ> | φ is a Boolean formula with at least two satisfying assignments} �Goal: �Show that Double-SAT is NP-Complete 20

Double-SAT (Proof Sketch) �Steps: 1) Show that Double-SAT ∈ NP 2) Show that Double-SAT is not easier than a certain NPC problem � For the NPC problem, we choose SAT � i. e. , we want to poly-time reduce Double-SAT to SAT 3) Show the correspondence of “yes” instance between reduction 21

Double-SAT - (1) NP �It is trivial to see that Double-SAT ∈ NP �Given 2 assignments for φ, and verify whether both of them satisfy φ �We can just evaluate the truth value in poly-time 22

Double-SAT - (2) Reduction �Reduction: �On input φ(x 1, . . . , xn): 1. Introduce a new variable w 2. Output formula φ’(x 1, . . . , xn, y) = φ(x 1, . . . , xn) ∧ ( w ∨ w ). x R x∈L SAT y y ∈ L’ Double-SAT TM for L’ acc rej TM accepts 23

Double-SAT - (3) Correspondence �x ∈ L y ∈ L’ � : Suppose there is an satisfying assignment, X, for φ(x 1, . . . , xn), we can find two satisfying assignments for φ’(x 1, . . . , xn, w): �Assignment 1 = {X, w=True} �Assignment 2 = {X, w=False} � φ’(x 1, . . . , xn, w) = φ(x 1, . . . , xn) ∧ ( w ∨ w ) For {xi}, assign X, then this part = True No matter what w is, this part = True 24

Double-SAT - (3) Correspondence �x ∈ L y ∈ L’ � : We use contrapositive �i. e. , to show x ∉ L ⇒ y ∉ L’ �Indeed, if x ∉ L, φ(x 1, . . . , xn)=False �Then, no matter what the value of y is �φ’(x 1, . . . , xn, y)=False 25

Dominating Set �Problem: �Dominating-set = {<G, K> | A dominating set of size K for G exists} �Goal: �Show that Dominating-set is NP-Complete 26

Dominating Set (Definition) �Problem: �Dominating-set = {<G, K> | A dominating set of size (at most) K for G exists} �Let G=(V, E) be an undirected graph �A dominating set D is a set of vertices that covers all vertices �i. e. , every vertex of G is either in D or is adjacent to at least one vertex from D 27

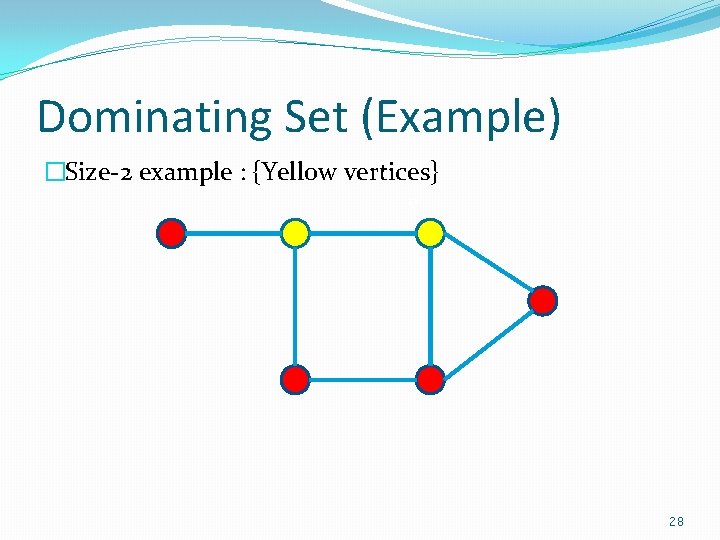
Dominating Set (Example) �Size-2 example : {Yellow vertices} e 28

Dominating Set (Proof Sketch) �Steps: 1) Show that Dominating-set ∈ NP. 2) Show that Dominating-set is not easier than a NPC problem � We choose this NPC problem to be Vertex cover � Reduction from Vertex-cover to Dominating-set 3) Show the correspondence of “yes” instances between the reduction 29

Dominating Set - (1) NP �It is trivial to see that Dominating-set ∈ NP �Given a vertex set D of size K, we check whether (V-D) are adjacent to D �i. e. , for each vertex, v, in (V-D), whether v is adjacent to some vertex u in D 30

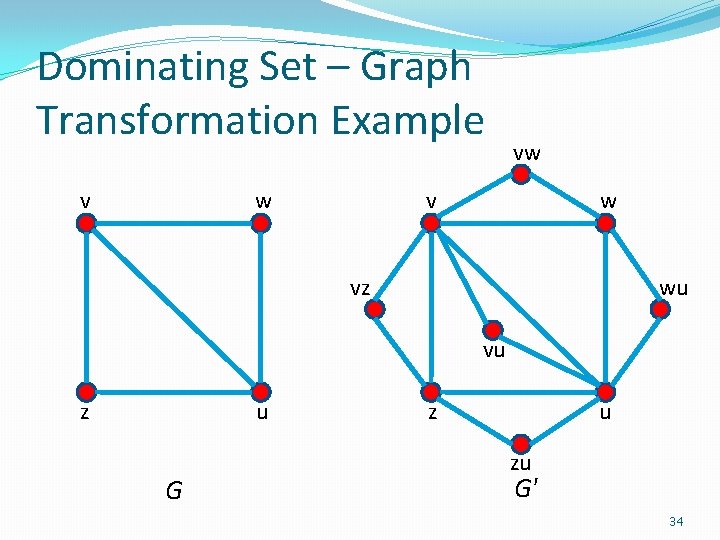
Dominating Set - (2) Reduction �Reduction - Graph transformation � Construct a new graph G' by adding new vertices and edges to the graph G as follows: G <G, k> ∈ L Vertex-cover T G’ <G’, k> ∈ L’ Dominating-set 31

Dominating Set - (2) Reduction �Reduction - Graph transformation (Con’t) � For each edge (v, w) of G, add a vertex vw and the edges (v, vw) and (w, vw) to G' � Furthermore, remove all vertices with no incident edges; such vertices would always have to go in a dominating set but are not needed in a vertex cover of G � We skip the discussion of this subtle part in the followings G <G, k> ∈ L Vertex-cover T G’ <G’, k> ∈ L’ Dominating-set 32

[Recap] Vertex cover �A vertex cover, C, is a set of vertices that covers all edges �i. e. , each edge is at least adjacent to some node in C 1 2 3 4 {2, 4}, {3, 4}, {1, 2, 3} are vertex covers 33

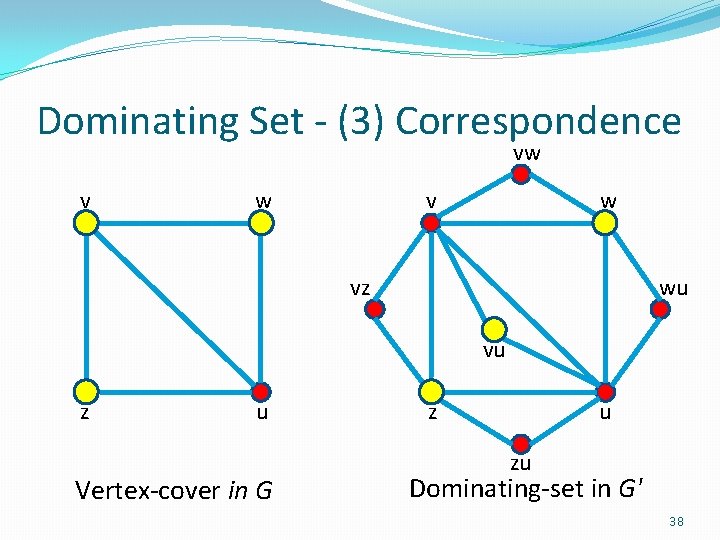
Dominating Set – Graph Transformation Example v w vw v w vz wu vu z u G z u zu G' 34

Dominating Set - (3) Correspondence �A dominating set of size K in G’ A vertex cover of size K in G � Let D be a dominating set of size K in G’ � Case 1): D contains only vertices from G Then, all new vertices have an edge to a vertex in D D covers all edges D is a valid vertex cover of G 35

Dominating Set - (3) Correspondence �A dominating set of size K in G’ A vertex cover of size K in G � Let D be a dominating set of size K in G’ � Case 2): D contains some new vertices (vertex in the form of uv) (We show to construct a vertex cover using only old vertices, otherwise we cannot obtain a vertex cover for G) For each new vertex uv, replace it by u (or v) If u ∈ D, this node is not needed Then the edge u-v in G will be covered After new edges are removed, it is a valid vertex cover of G (of size at most K) 36

Dominating Set - (3) Correspondence �A dominating set of size K in G’ A vertex cover of size K in G � Let C be a vertex cover of size K in G For an old vertex, v ∈ G’ : � By the definition of VC, all edges incident to v are covered � v is also covered For a new vertex, uv ∈ G’ : � Edge u-v must be covered, either u or v ∈ C � This node will cover uv in G’ Thus, C is a valid dominating for G’ (of size at most K) 37

Dominating Set - (3) Correspondence vw v w vz wu vu z u Vertex-cover in G z u zu Dominating-set in G' 38

End Any questions? (There should be some) 39