NMEROS PRIMOS ADRIANA MILENA VILA REYES LICENCIATURA EN























- Slides: 23

NÚMEROS PRIMOS ADRIANA MILENA ÁVILA REYES LICENCIATURA EN MATEMÁTICAS

Un poco de historia 1732 Euler 300 a. C Euclides 600 a. C Pitágoras 1632 Fermat 1914 Lehmer 1752 Goldbach D. H Lehmer

Los números primos han inquietado a los matemáticos desde tiempos inmemoriales y han surgido numerables problemas que fascinan y motivan la imaginación, aunque algunos aun permanecen sin solución Existe siempre un primo por lo menos entre para cada entero n>1? ¿Contiene la secuencia de Fibonacci un número infinito de primos?

DEFINICIÓN Decimos que a es un numero primo si a es mayor que 1 y sus únicos divisores positivos son 1 y a, en caso contrario a se llama compuesto. en consecuencia, los números primos menores que 100 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.

INFINITUD DE LOS NÚMEROS PRIMOS Proposición: los números primos son infinitos Demostración de Euclides. Esta demostración aparece en el año 300 antes de Cristo en el IX libro de la colección de trece llamada “ELEMENTOS” de Euclides y es un bonito ejemplo del método de demostración por reducción al absurdo.

demostración ejemplo Supongamos que hay un numero finito de números primos , Supongamos que los únicos números primos que existen son 2, 3, 5 y 7 Sea N= 2*3*5*7+1 primo de N Como n es un número compuesto , debe dejarse dividir por al menos uno de los primos. N=211 Pero al dividir n por cada residuo 1. me deja Lo que contradice la definición de divisibilidad Por lo tanto existen números primos infinitos y 2 es un divisor

Polinomios que me permiten obtener números primos

Teorema: existen infinitos primos de la forma 4 x+1 Demostración. Sea a >1 un entero, demostraremos que existe un primo p>a tal que p es de la forma 4 x+1. Sea m=(a!)²+1, obsérvese que m es impar y m >1 Sea p el menor número primo que divide a m, es claro que 2, 3, …, a-1, a no son divisores de m ; así que p>a y p divide a m =(a!)²+1. Además tenemos, (a!)²+1=kp, para algún k entero.

Por lo tanto (a!)² (-1)( modulo p) Elevando ambos miembros de esta congruencia a la potencia (p-1)/2, obtenemos Por el teorema de euler-fermat tenemos que y por lo tanto Así que

Luego Así que , y esta diferencia debe ser divisible por p (p es primo mayor que 2), entonces la única posibilidad es que z= 0 Es decir que Luego Finalmente se tiene que p=4 x+1

Fermat descubrió que todo número primo de la forma 4 x+1 tal como 5, 13, 17, 29, 37, …. . es una suma de dos cuadrados.

Teorema: Existen infinitos primos de la forma 4 x-1 Demostración. Supongamos que hay un número finito de primos de esta forma, y sea p el mayor de todos ellos. Consideremos ahora el entero a = 4(3*5*7*…* p )-1 a no puede ser primo ya que a > p

Además, ningún primo menor o igual que p divide a a , por lo que todos los factores primos de a exceden a p. Pero no es posible que todos los factores primos de a sean de la forma 4 x+1, puesto que el producto de dos de tales números es de la misma forma. Luego algún factor primo de a debe ser de la forma 4 x 1, lo que constituye una contradicción.

ALGUNAS CLASES DE NÚMEROS PRIMOS DE MERSENNE NUMERO PRIMO DE FERMAT NUMERO PRIMO DE SOPHIE GERMAIN NUMEROS PRIMOS GEMELOS NÚMEROS PRIMOS REVERSIBLES

37, 156, 667 2 -1 11, 185, 272 dígitos

GRÁCIAS

Por ejemplo 5 =1²+2² 13=2²+3² 17=1²+4² 29=2²+5² 37=1²+6² 41=4²+5²

DEFINICIÓN : si a y b son enteros, decimos que a divide a b si existe un entero c tal que b=a*c

NÚMERO PRIMO DE MERSENNE Se dice que un número M es un número de Mersenne si es una unidad menor que una potencia de 2. Mn = 2 n − 1. Un número primo de Mersenne es un número de Mersenne que es primo.

NÚMERO PRIMO DE FERMAT Pierre de Fermat conjeturó que todos los números naturales de la forma 22 n + 1, con n natural eran números primos

NÚMERO PRIMO DE SOPHIE GERMAIN Un número primo p es un número de Sophie Germain si 2 p+1 también es número primo. Ejemplo: con p=2, 2 x 2+1=5 que también es un número primo.

NÚMEROS PRIMOS GEMELOS Dos números primos (p, q) son números primos gemelos si están separados por una distancia de 2, es decir, si.

NUMEROS REVERSIBLES son aquellos que al leerlos al revés (de derecha a izquierda) dan un nuevo número primo. Ej. 13 y 31 o 1201 y 1021
 Factores primos de 60
Factores primos de 60 Nyuexternal
Nyuexternal Nmeros reales
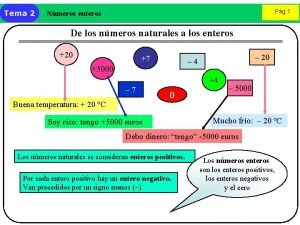
Nmeros reales Nmeros enteros
Nmeros enteros Nmeros naturales
Nmeros naturales Numeros romanos
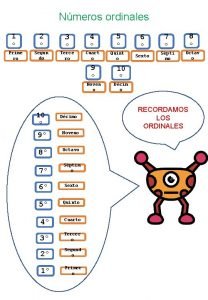
Numeros romanos Nmeros ordinales
Nmeros ordinales Nmeros enteros
Nmeros enteros Numeral cardinal
Numeral cardinal Nmeros ordinales
Nmeros ordinales Numeros pentagonales
Numeros pentagonales Nmeros enteros
Nmeros enteros Nmeros ordinales
Nmeros ordinales Nmeros ordinales
Nmeros ordinales Nmeros
Nmeros Primero, segundo, tercero cuarto
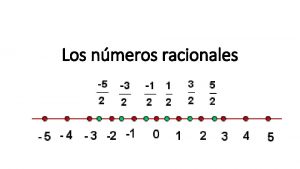
Primero, segundo, tercero cuarto Recta numerica de numeros enteros
Recta numerica de numeros enteros Nmeros romanos
Nmeros romanos Nmeros romanos
Nmeros romanos Nmeros reales
Nmeros reales Nmeros naturales
Nmeros naturales Ejercicios de números romanos para imprimir
Ejercicios de números romanos para imprimir Costo de conversion
Costo de conversion (our) primos son canadienses.
(our) primos son canadienses.