Mtodos Numricos para EDOs 2007 2 1 Mtodos

Métodos Numéricos para EDO’s 2007. 2 1

Métodos Numéricos para EDO’s • Esta parte compreende métodos que aproximam uma equação diferencial por uma equação de diferenças. – Uma equação de diferenças de ordem n é uma sequência de equações da forma gk(yk+n, yk+n-1, … yk) = 0 yi = i k= 0, 1, 2, … (9) i = 0, 1, 2, …, n-1 – Os gksão funções de n+1 variáveis e os valores i, i = 0(1)n-1, são específicos. Uma solução de tal equação é uma sequência {y 0, y 1, y 2, y 3, …, yn-1, yn} que satisfaz a (9). 2007. 2 2

Métodos Numéricos para EDO’s • Note que determinar numericamente uma solução de uma equação diferencial é encontrar os valores y 1, y 2, …, yn através de uma aproximação da equação de diferenças. – Essa aproximação introduz um erro de truncamento e um erro de arredondamento 2007. 2 3

Métodos Numéricos para EDO’s • Os métodos de passos simples necessitam apenas dos resultados de yk , do passo anterior, para determinar a aproximação de yk+1. • Os métodos de passos múltiplos servem para determinar a aproximação yk+1 a qual depende dos valores de yk, yk-1. . . 2007. 2 4

Métodos de Euler • O método de Euler é um método mais simples que oferece solução para EDOs com condições iniciais. • A simplicidade do método serve ilustrar técnicas usadas em outros métodos. • Ele consiste em aproximar a solução y ( x ), no sentido de uma linearização, por meio de suas tangentes (vide próximo slide). 2007. 2 5

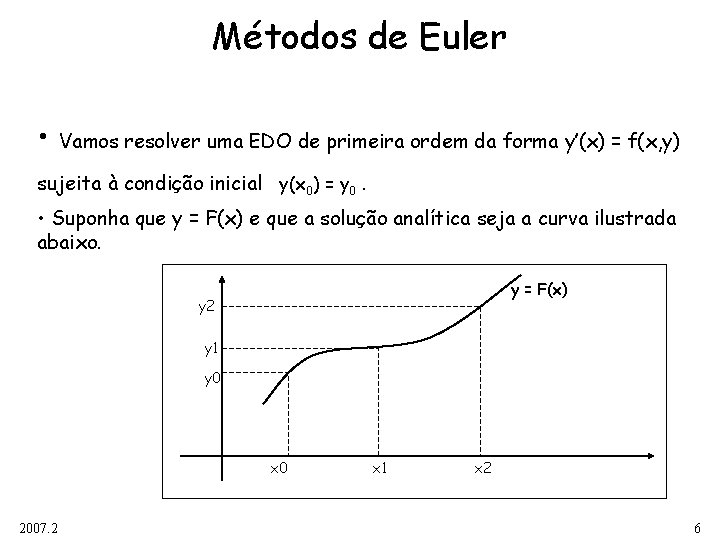
Métodos de Euler • Vamos resolver uma EDO de primeira ordem da forma y’(x) = f(x, y) sujeita à condição inicial y(x 0) = y 0. • Suponha que y = F(x) e que a solução analítica seja a curva ilustrada abaixo. y = F(x) y 2 y 1 y 0 x 0 2007. 2 x 1 x 2 6

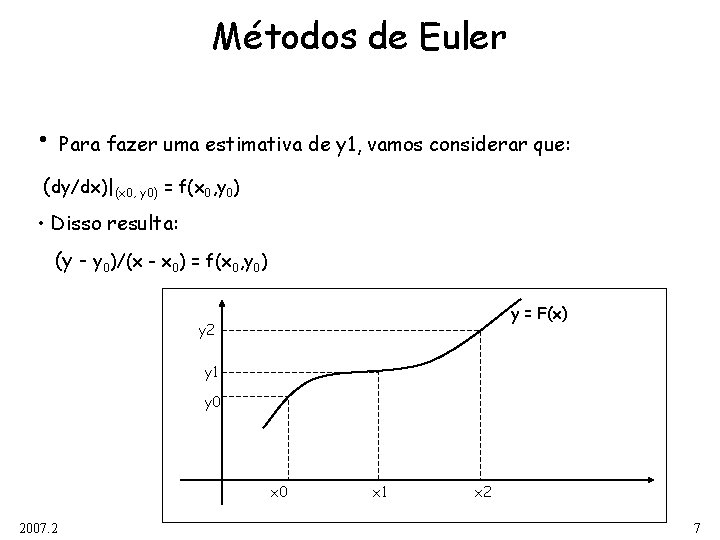
Métodos de Euler • Para fazer uma estimativa de y 1, vamos considerar que: (dy/dx)|(x 0, y 0) = f(x 0, y 0) • Disso resulta: (y - y 0)/(x - x 0) = f(x 0, y 0) y = F(x) y 2 y 1 y 0 x 0 2007. 2 x 1 x 2 7

Métodos de Euler • Considerando que se h = x - x do ponto Q, y tende a y 1 e daí: 1 0 tender a zero, teremos que a ordenada y = y 0 + hf(x 0, y 0) ou y 1 y 0 + hf(x 0, y 0) Q = (x 1, y) y P 1 = (x 1, y 1) y 1 yk+1 = yk + hf(xk, yk) y 0 x 0 2007. 2 Generalizando, obtemos a seguinte equação de diferenças: x 1 que é a expressão do Método de Euler. 8

Métodos de Euler (2) • Outra interpretação do método de Euler • Considere o problema • i. e. , são dados um ponto de partida, (x 0, y 0), e uma direção a ser tomada, f (x, y ). • Desejamos determinar y (z ). 2007. 2 9

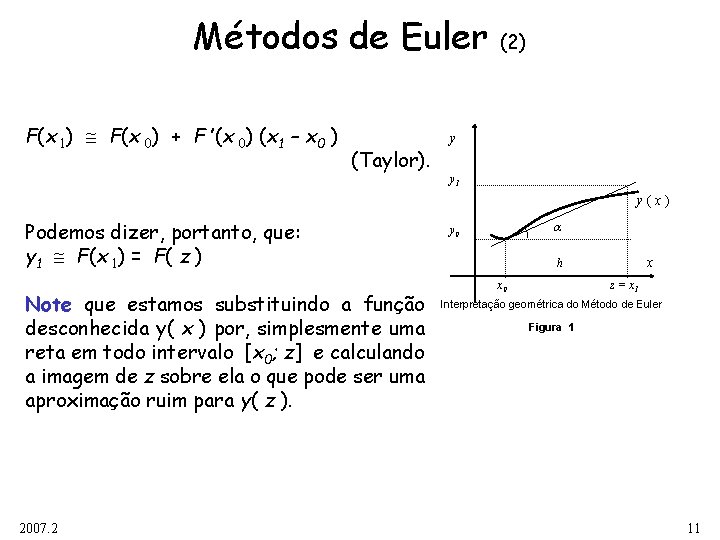
Métodos de Euler Considere a Figura 1. A interpretação geométrica da figura nos permite escrever a equação: F ’(x 0 ) = y’ (x 0) = f (x 0 , y 0) Fazendo y(x) y 0 Obteremos y 1 = y 0 + h f (x 0 , y 0) x h x 0 z = x 1 Interpretação geométrica do Método de Euler ou 2007. 2 y y 1 x 1 – x 0 = h F(x 1) F(x 0) + F ’(x 0) (x 1 – x 0 ) (2) Figura 1 (Taylor). 10

Métodos de Euler F(x 1) F(x 0) + F ’(x 0) (x 1 – x 0 ) (Taylor). (2) y y 1 y(x) Podemos dizer, portanto, que: y 1 F(x 1) = F( z ) Note que estamos substituindo a função desconhecida y( x ) por, simplesmente uma reta em todo intervalo [x 0; z] e calculando a imagem de z sobre ela o que pode ser uma aproximação ruim para y( z ). 2007. 2 y 0 x h x 0 z = x 1 Interpretação geométrica do Método de Euler Figura 1 11

Métodos de Euler • Todavia, note que podemos melhorar esta aproximação. Para isso, devemos subdividir o intervalo [x 0; z] em subintervalos de amplitude constante, genericamente chamada de h. • Como sabemos calcular a direção da função incógnita y(x) em cada ponto, bastar substituir essa função por um segmento de reta, em cada um destes subintervalos. • Note que estes segmentos terão a direção que ela (função) tem no início de cada dos subintervalos, (veja Figura 2). • Assim, obtemos: yi + 1 = yi + hf(xi, yi), i = 0, 1, 2, . . . (2) y y(x) y 2 y 1 y 0 h x 0 x h x 1 z = x 2 Método de Euler considerando dois subintervalos Figura 2 que vem a ser o método de Euler. 2007. 2 12

Métodos de Euler 2007. 2 (2) 13

Método Modificado de Euler • Um problema que ocorre no método “simples” de Euler é que ele pressupõe que a função que está sendo aproximada mantém, em todo intervalo, a direção que ela tem no extremo “de partida” dele. • • O método modificado de Euler irá considerar também uma única direção para a função y ( x ), só que uma direção média entre aquela do “início” do intervalo e uma estimativa da direção no “final” dele. • • Para tanto, em primeiro lugar, usando o método “simples” de Euler, fazemos uma previsão de yi + 1, chamada yi+1. 2007. 2 14

Método Modificado de Euler Dessa forma, Previsão : yi + 1 = yi + hf (xi , yi ). Com esta previsão, podemos obter o valor aproximado da direção da curva y(x) no ponto (xi + 1, yi + 1) através de f(xi + 1, y i + 1). Determina-se a chamada correção, Correção : yi + 1 = yi + h/2[f(xi, yi) + f(xi + 1, yi + 1)]. 2007. 2 15

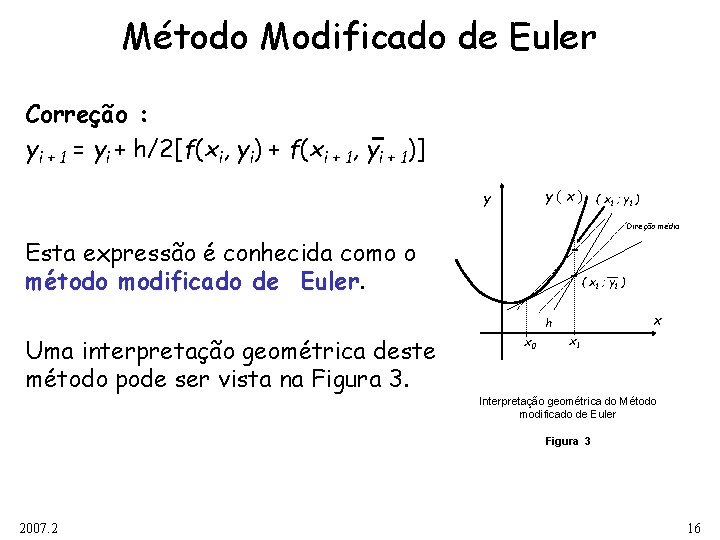
Método Modificado de Euler Correção : yi + 1 = yi + h/2[f(xi, yi) + f(xi + 1, yi + 1)] y(x) y ( x 1 ; y 1 ) Direção média Esta expressão é conhecida como o método modificado de Euler. ( x 1 ; y 1 ) x h Uma interpretação geométrica deste método pode ser vista na Figura 3. x 0 x 1 Interpretação geométrica do Método modificado de Euler Figura 3 2007. 2 16

Método Modificado de Euler Exemplo - Encontrar a solução da equação diferencial ordinária y’ = f (x, y ) = 2 x + 3 com a condição de valor inicial y ( 1) = 1. Dividindo o intervalo [1; 2 ] em apenas uma parte, i. e, fazendo h =1 e, aplicando o método de modificado de Euler, determine o valor aproximado de y(2) para a equação dada. 2007. 2 17

Método Modificado de Euler Solução Sabendo que a cada aproximação é necessário fazer um processo de previsão – correção e, considerando h =1, temos yi + 1 Previsão yi+1 = yi + hf(xi , yi ) no caso y 1 = y 0 + hf(x 0, y 0) y 1 = 1 + 1 f(1, 1) = 1 + 1 (2 x 1 + 3) = 6 2007. 2 18

Método Modificado de Euler Solução Correção yi+1 = yi + h/2[f(xi , yi ) + f(xi+1 , yi+1)] y 1 = 1 + ½[f(1, 1) + f(2, 6)] y 1 = 1 + 1/2[5 + 2 x 2+3] = 1 + 6 = 7. 2007. 2 19

Referências Ruggiero, M. A. G. , Lopes, V. L. R. , Cálculo Numérico – Aspectos Teóricos e Computacionais, Pearson/Markron Books, 2 a. Edição, 1998. Cláudio, D. M. e Martins, J. M. , Cálculo Numérico Computacional, Ed. Atlas, 1987. Barroso, L, Barroso, M. M. A. , Campos Filho, F. F. , Cálculo Numérico com Aplicações, Ed. Harbra, 1987. 2007. 2 20