Modern Control Systems MCS Lecture7 Phase Plane Analysis

Modern Control Systems (MCS) Lecture-7 Phase Plane Analysis Dr. Imtiaz Hussain Assistant Professor email: imtiaz. hussain@faculty. muet. edu. pk URL : http: //imtiazhussainkalwar. weebly. com/ 1

Introduction • The definition for stability for LTI systems is an easy concept to understand (eigenvalues). • It is necessary to extend the concept of stability to nonlinear systems. 2

Basic Idea • To generate motion trajectories corresponding to various initial conditions in the phase plane. • To examine the qualitative features of the trajectories. • In such a way, information concerning stability and other motion patterns of the system can be obtained. 3

State Space Trajectories • The unforced response of a system released from any initial point x(to) traces a curve or trajectory in state space, with time t as an implicit function along the trajectory. • When state variables are represented as phase variables, the state space is called phase space or phase plane. • The family of all trajectories (which started by different initial points) is called phase portrait. 4

Phase Plane Analysis • A graphical method: to visualize what goes on in a nonlinear system without solving the nonlinear equations analytically. • 2. Limitation: limited for second-order (or first –order) dynamic system; however, some practical control systems can be approximated as second-order systems. 5

How to Plot? • There a number of methods for constructing phase plane trajectories for linear or nonlinear system, such as 1. 2. 3. 4. 5. 6. 7. Solution of state equations analytical method The method of isoclines The delta method Lienard’s method Pell’s method Software Programs (based on above six methods) 6

Phase Plane Analysis of Linear Systems 7

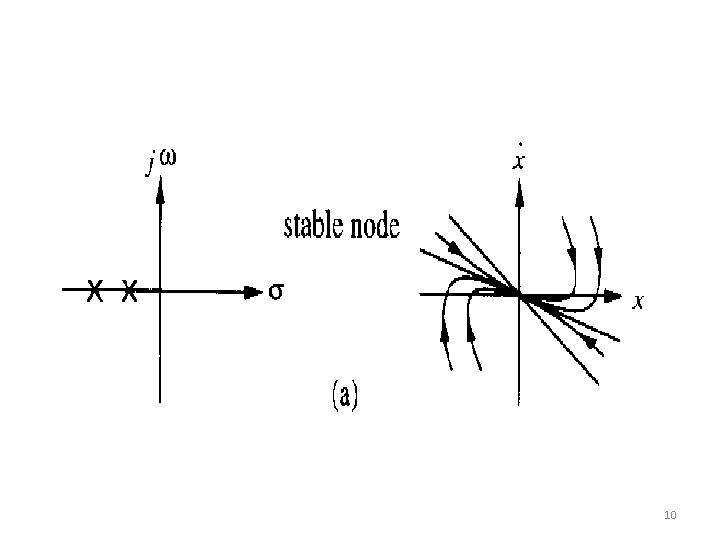
- Consider the second-order linear system is the general solution • Where the eigenvalues and are the solutions of the characteristic equation 8

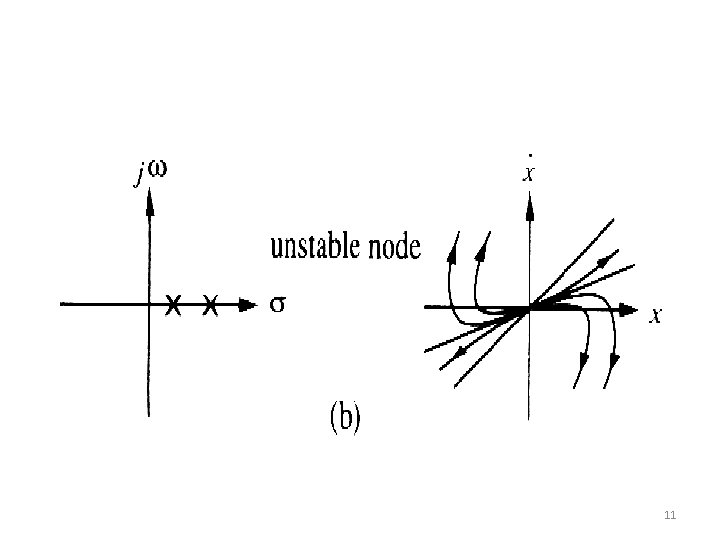
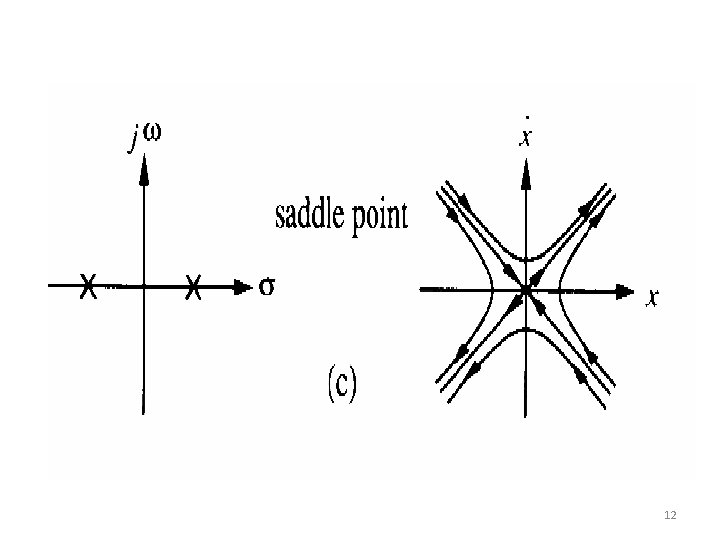
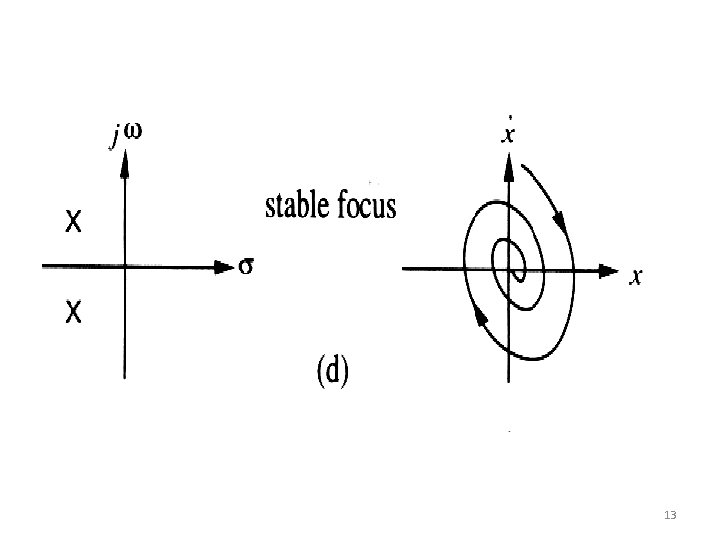
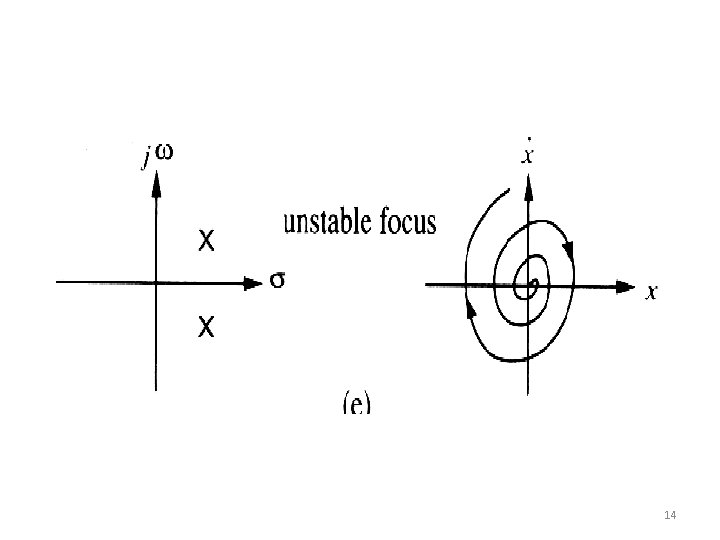
There is only one singular point (assuming ), namely the origin. 1. and are both real and have the same sign (positive or negative) 2. and are both real and have opposite signs (saddle point) 3. and real parts are complex conjugate with non-zero 4. and are complex conjugates with real parts equal to zero (center point) 9

10

11

12

13

14

Phase Portrait of LTI Systems • 15

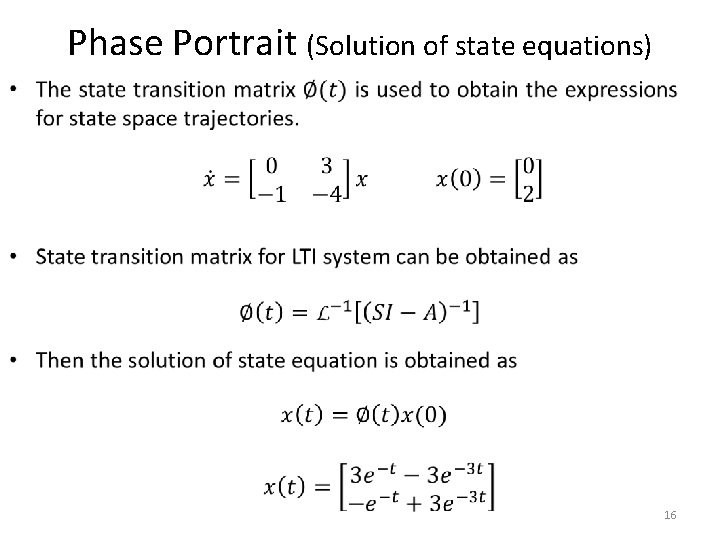
Phase Portrait (Solution of state equations) • 16

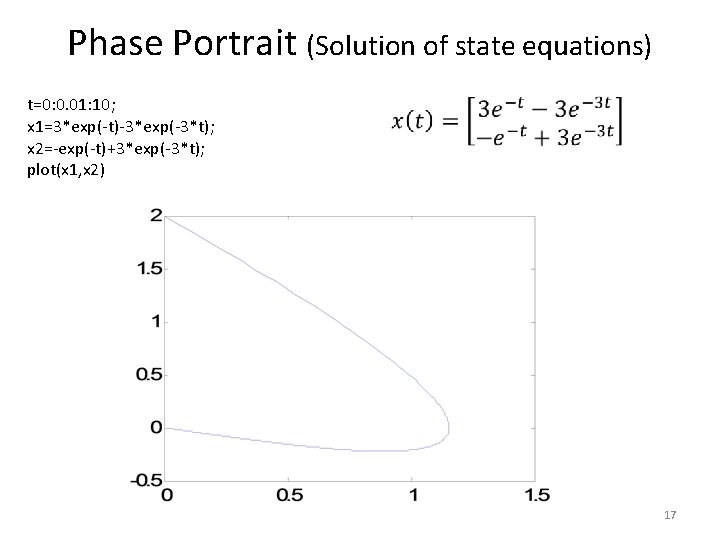
Phase Portrait (Solution of state equations) t=0: 0. 01: 10; x 1=3*exp(-t)-3*exp(-3*t); x 2=-exp(-t)+3*exp(-3*t); plot(x 1, x 2) 17

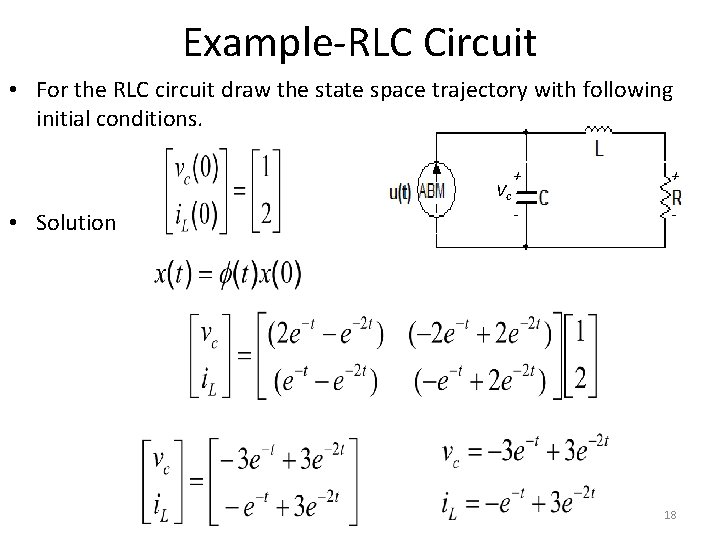
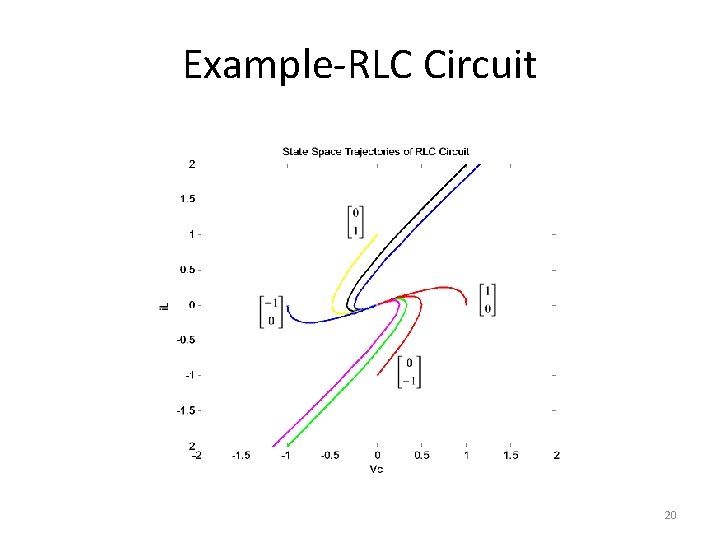
Example-RLC Circuit • For the RLC circuit draw the state space trajectory with following initial conditions. Vc • Solution + + - - 18

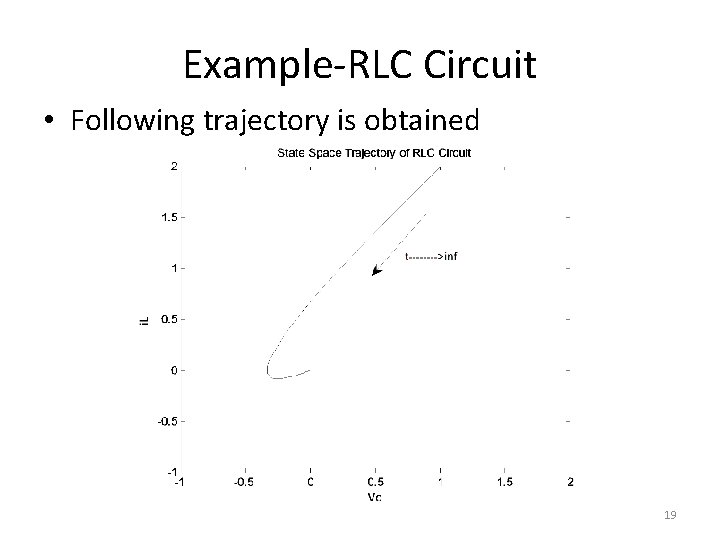
Example-RLC Circuit • Following trajectory is obtained 19

Example-RLC Circuit 20

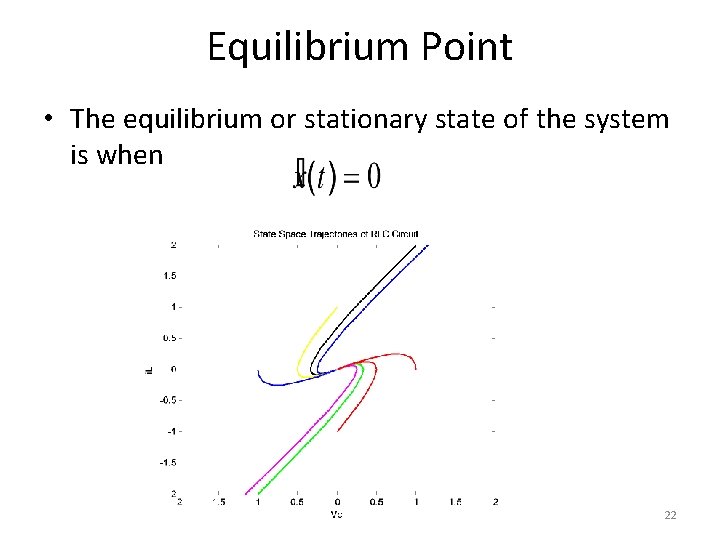
Equilibrium Point and Singular Points • Equilibrium point is defined as a point where the system states can stay forever • This implies that • 21

Equilibrium Point • The equilibrium or stationary state of the system is when 22

Examples of LTI systems • 23

Software Solution • x 1 dom = linspace(-5, 5, 51); x 2 dom = linspace(-5, 5, 51); [x 1, x 2] = meshgrid(xdom, ydom); % generate mesh of domain x 1 dot = x 1; % dx 1/dt X 2 dot= = -x 1 -4*x 2; % dx 2/dt quiver(x 1, x 2, x 1 dot, x 2 dot) % velocity Vectors 24

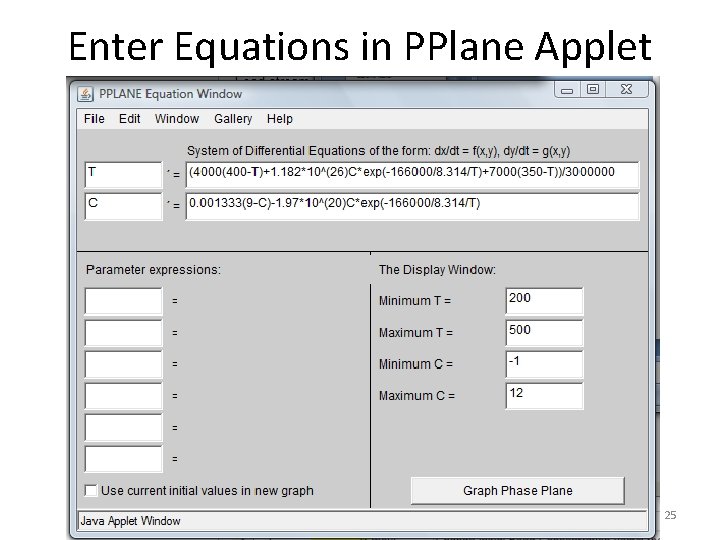
Enter Equations in PPlane Applet 25

Phase Plane Analysis of Nonlinear Systems 26

Introduction • In discussing the phase plane analysis of nonlinear systems, two points should be kept in mind: – Phase plane analysis of nonlinear systems is related to that of liner systems, because the local behavior of nonlinear systems can be approximated by the behavior of a linear system. – Nonlinear systems can display much more complicated patterns in the phase plane, such as multiple equilibrium points and limit cycles. 27

Example

Equilibrium States

Example: Simple Pendulum • Consider the pendulum shown in figure. Where, L: the pendulum’s length M: its mass b: the friction coefficient at the hinge g: the gravity constant.

Example: Simple Pendulum • State equation of the system are given as

• The equilibrium points: x 2 = 0, sin x 1 = 0 (0, 0) and (π, 0) • The pendulum resting exactly at the vertical up and down positions.

Example • Consider a nonlinear system described by following state equations determine the number of equilibrium point(s) of the system. Answer (1, 1) and (− 1, − 1). 33

Example • Consider a nonlinear system described by following state equations determine the number of equilibrium point(s) of the system. Answer (0, 0) and (− 1/2, 1). 34

Local Behavior of Nonlinear Systems • If the singular point of interest is not at the origin, by defining the difference between the original state and the singular point as a new set of state variables, we can shift the singular point to the origin. • Using Taylor expansion a second order nonlinear system can be rewritten in the form 35

Local Behavior of Nonlinear Systems • In the vicinity of the origin, the higher order terms can be neglected, and therefore, the nonlinear system trajectories essentially satisfy the linearized equation • As a result, the local behavior of the nonlinear system can be approximated by the patterns shown by linear systems 36

Limit Cycle • In the phase plane, a limit cycle is defied as an isolated closed curve. • The trajectory has to be both closed, indicating the periodic nature of the motion, and isolated, indicating the limiting nature of the cycle (with near by trajectories converging or diverging from it). 37

Limit Cycle • Depending on the motion patterns of the trajectories in the vicinity of the limit cycle, we can distinguish three kinds of limit cycles. – Stable Limit Cycles: all trajectories in the vicinity of the limit cycle converge to it as t →∞ – Unstable Limit Cycles: all trajectories in the vicinity of the limit cycle diverge to it as t →∞ 38

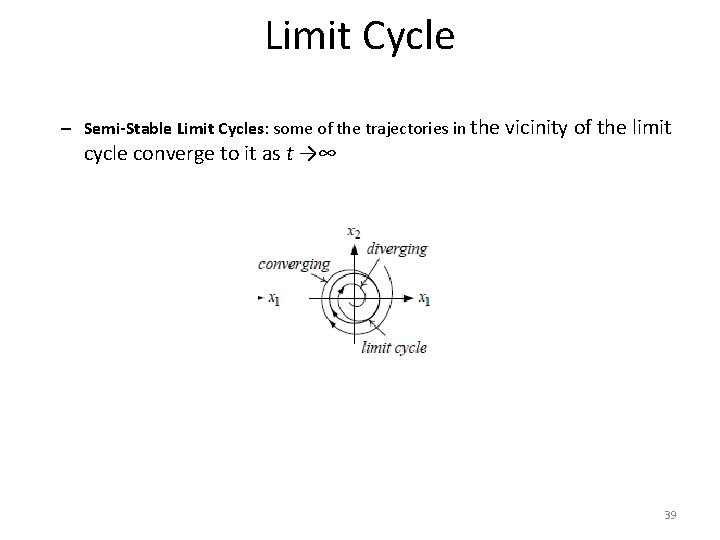
Limit Cycle – Semi-Stable Limit Cycles: some of the trajectories in the vicinity of the limit cycle converge to it as t →∞ 39

Example • Find the equilibrium point(s) of the nonlinear system. Then determine the type and stability of each equilibrium point. • If system exhibits limit cycles then determine the nature of limit cycle as well. 40

Example • Find the equilibrium point(s) of each nonlinear system given below. Then determine the type and stability of each equilibrium point. 1). 2). • If system exhibits limit cycles then determine the nature of limit cycle as well. 41

Exercise • Find the equilibrium point(s) of each nonlinear system given below. Then determine the type and stability of each equilibrium point. If system exhibits limit cycles then determine the nature of limit cycle as well. 1). 2). 4). 5). 3). 42

Solution 1). • Equilibrium points are (0, 0) and (− 3, 3). • (0, 0) is a stable center, • (− 3, 3) is an unstable saddle point. 43

Solution 2). • Equilibrium points are (0, 1) and (1/4, 3/4) • (0, 1) is an unstable saddle point, • (1/4, 3/4) is an unstable spiral point. 44

Solution 3). • • • Equilibrium points are (2, 3), (2, − 3), (3, 2) and (− 3, 2). (2, 3) is an unstable saddle point (2, − 3) is an unstable saddle point (3, 2) is an unstable node, (− 3, 2) is an asymptotically stable node. 45

Solution 4). • • Equilibrium points are (1, 1), (1, − 1), (− 1, 1), and (− 1, − 1). (1, 1) is an asymptotically stable spiral point, (1, − 1) and (− 1, 1) both are unstable saddle points, (− 1, − 1) is an unstable spiral point. 46

Solution 5). • • Equilibrium points are (0, 0), (2, 4), and (− 5, 4). (0, 0) is an unstable saddle point, (2, 4) is an unstable node, (− 5, 4) is an asymptotically stable node. 47

To download this lecture visit http: //imtiazhussainkalwar. weebly. com/ END OF LECTURE-7 48