MCS 312 NP Completeness and Approximation algorithms Instructor

MCS 312: NP Completeness and Approximation algorithms Instructor Neelima Gupta ngupta@cs. du. ac. in

Table of Contents • Hamiltonian Cycle

Hamiltonian Cycle Problem A Hamiltonian cycle in a graph is a cycle that visits each vertex exactly once Given Problem Statement A directed graph G = (V, E) To Find If the graph contains a Hamiltonian cycle

Hamiltonian Cycle Problem is NP-Complete Hamiltonian Cycle Problem is in NP. Given a directed graph G=(V, E), and a certificate containing an ordered list of vertices on a Hamiltonian Cycle. It can be verified in polynomial time that the list contains each vertex exactly once and that each consecutive pair in the ordering is joined by an edge.

Hamiltonian Cycle Problem is NP Hard 3 -SAT ≤p Hamiltonian Cycle We begin with an arbitrary instance of 3 S A T h a v i n g v a r i a b l e s x 1 , … …. , xn a n d clauses C 1, ……. , Ck W e m o d e l o n e b y o n e , t h e 2 n different ways in which variables can assume assignments, and the constraints imposed by clauses.

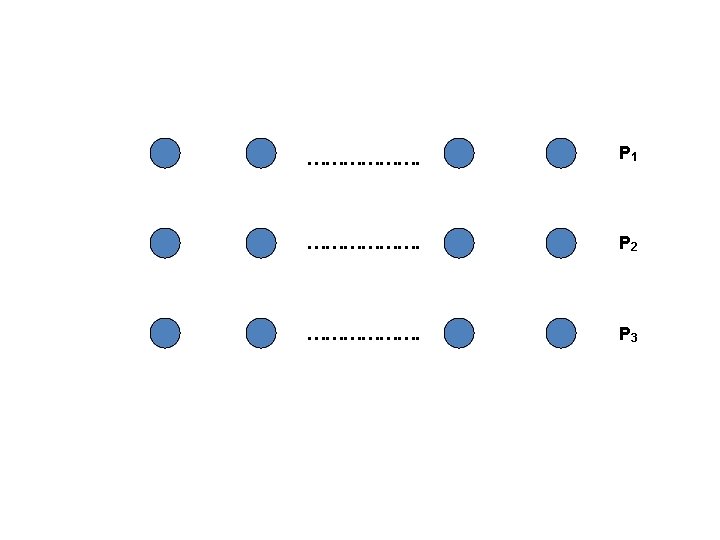
Hamiltonian Cycle Problem To correspond to the 2 n truth assignments, we describe a graph containing 2 n different Hamiltonian cycles. The graph is constructed as follows: Construct n paths P 1, ……. , Pn. • Each Pi consists of nodes vi 1, …. . , vib, where b = 2 k (k being the number of clauses)

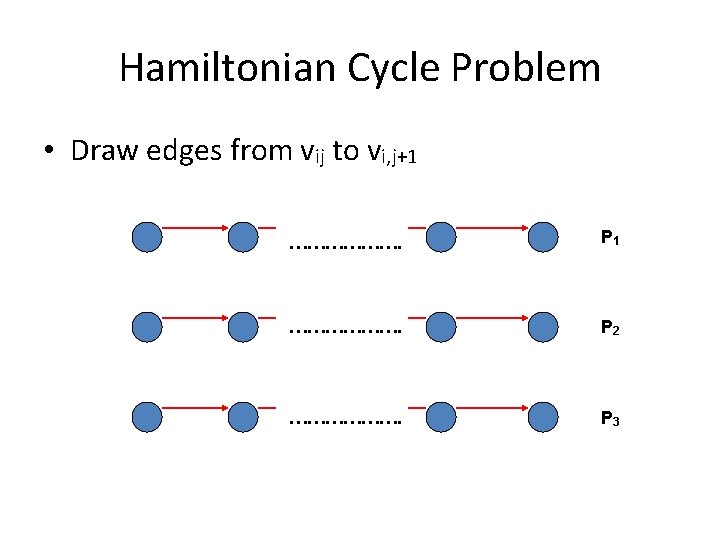
Hamiltonian Cycle Problem • Draw edges from vij to vi, j+1 ………………. P 2 ………………. P 3

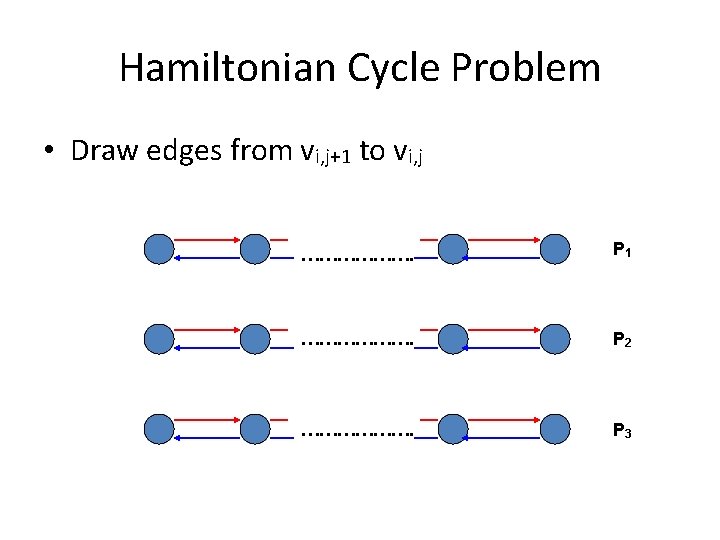
Hamiltonian Cycle Problem • Draw edges from vi, j+1 to vi, j ………………. P 1 ………………. P 2 ………………. P 3

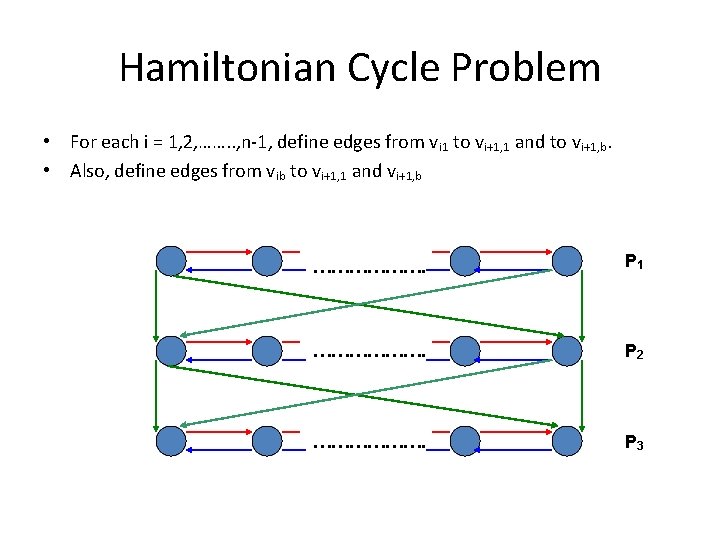
Hamiltonian Cycle Problem • For each i = 1, 2, ……. . , n-1, define edges from vi 1 to vi+1, 1 and to vi+1, b. • Also, define edges from vib to vi+1, 1 and vi+1, b ………………. P 1 ………………. P 2 ………………. P 3

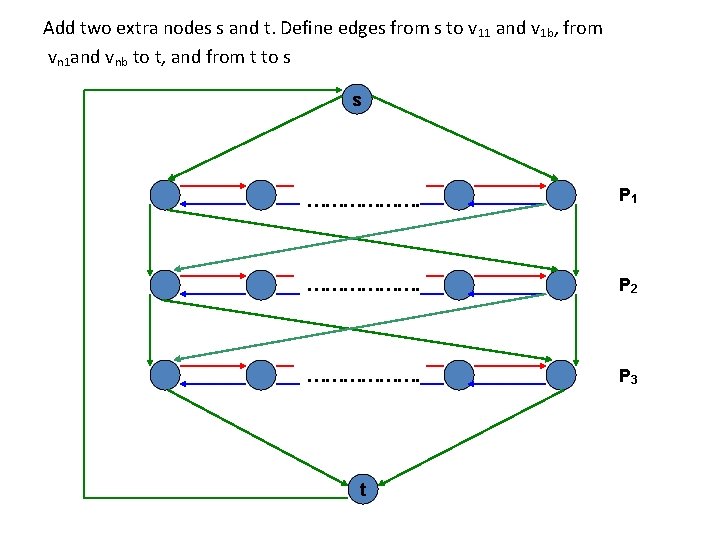
Add two extra nodes s and t. Define edges from s to v 11 and v 1 b, from vn 1 and vnb to t, and from t to s s ………………. P 1 ………………. P 2 ………………. P 3 t

Hamiltonian Cycle Problem Observations: Ø Any Hamiltonian cycle must use the edge (t, s) Ø Each Pi can either be traversed left to right or right to left. This gives rise to 2 n Hamiltonian cycles. Ø We have therefore modeled the n independent choices of how to set each variable; if Pi is traversed left to right, xi=1, else xi=0

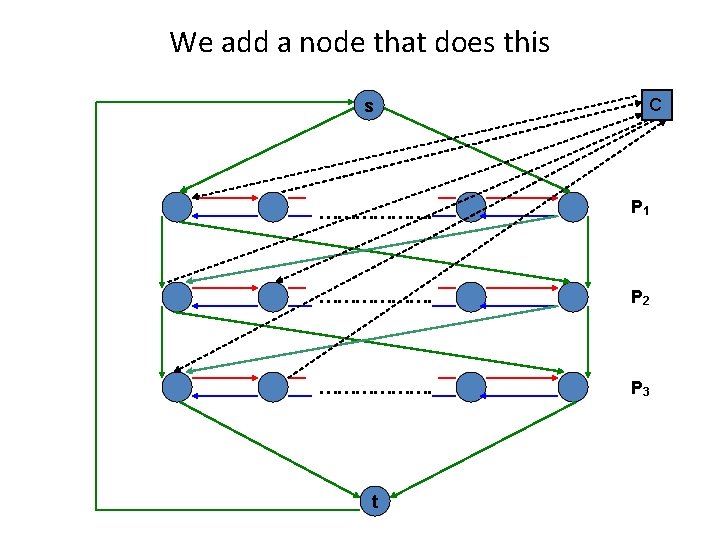
Hamiltonian Cycle Problem We now add nodes to model the clauses Consider the clause C = (x 1’ν x 2 ν x 3’) What is the interpretation of the clause? The path P 1 should be traversed right to left, or P 2 should be traversed left to right, or P 3 right to left.

Hamiltonian Cycle Problem In general • We define a node cj for each clause Cj. • In each path Pi, positions 2 j-1 and 2 j are reserved for variables that participate in clause Cj • If Cj contains xi, add edges (vi, 2 j-1 , cj)and (cj , vi, 2 j) • If Cj contains xi’, add edges (vi, 2 j , cj)and (cj, vi, 2 j-1) Gadget constructed !

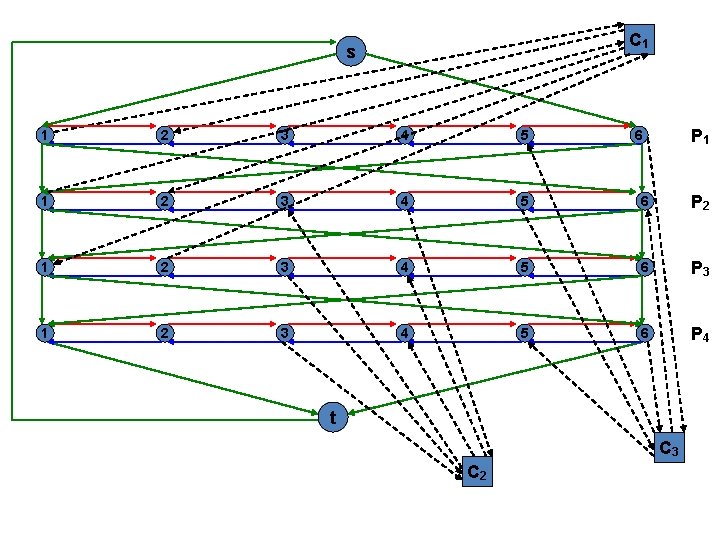
Hamiltonian Cycle Problem Consider an instance of 3 -SAT having 4 variables : x 1, x 2 x 3, x 4 3 clauses C 1 : (x 1 v x 2 v x 3’) C 2 : (x 2’ v x 3 v x 4) C 3 : (x 1’ v x 2 v x 4’)

Hamiltonian Cycle Problem We reduce the given instance as follows: n = 4 k = 3 b= 2*3 = 6 Construct 4 paths P 1, P 2, P 3, P 4 P 1 consists of nodes v 1, 1, v 1, 2 , ……. . , v 1, 6 P 2 consists of nodes v 2, 1, v 2, 2 , ……. . , v 2, 6 P 3 consists of nodes v 3, 1, v 3, 2 , ……. . , v 3, 6 P 4 consists of nodes v 4, 1, v 4, 2 , ……. . , v 4, 6

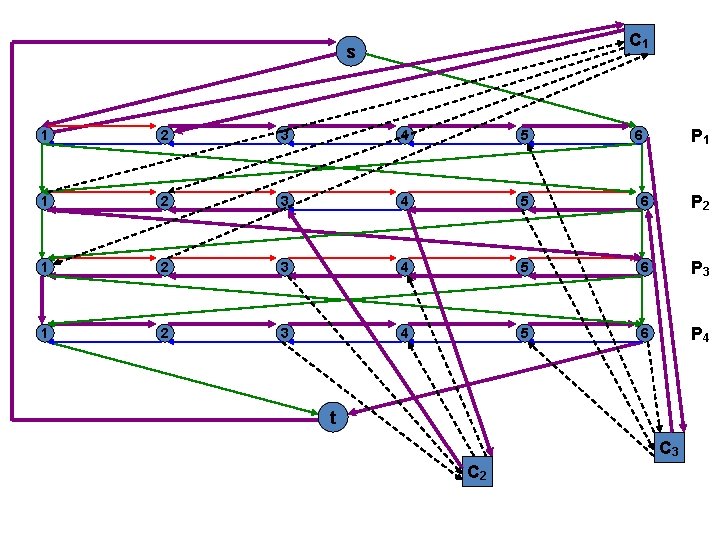
C 1 s P 1 1 2 3 4 5 6 P 2 1 2 3 4 5 6 P 3 1 2 3 4 5 6 P 4 t C 3 C 2

Hamiltonian Cycle Problem C l a i m: 3 - S A T i n s t a n c e i s s a t i s f i a b l e i f a n d o n l y i f G has a Hamiltonian cycle Proof: Part I G i v e n A satisfying assignment for the 3 -SAT instance I f xi = 1 , t r a v e r s e P i l e f t t o r i g h t , e l s e r i g h t t o l e f t. S i n c e e a c h c l a u s e Cj i s s a t i s f i e d b y t h e a s s i g n m e n t , there has to be at least one path Pi that moves in the right direction to be able to cover node cj. This Pi can be spliced into the tour there via edges incident on vi, 2 j-1 and vi, 2 j

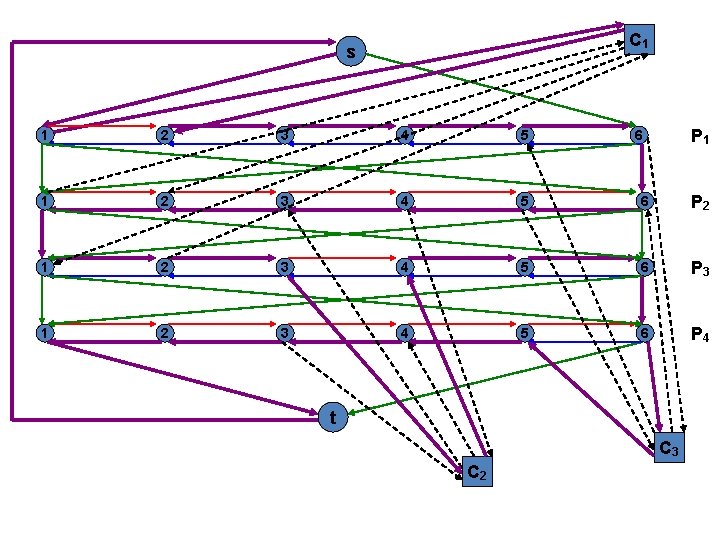
Hamiltonian Cycle Problem Let us try to verify this with our example Given A satisfying assignment for 3 -SAT, say x 1 = 1 x 2 = 0 x 3 = 1 x 4 = 0 Let us check out a corresponding Hamiltonian cycle

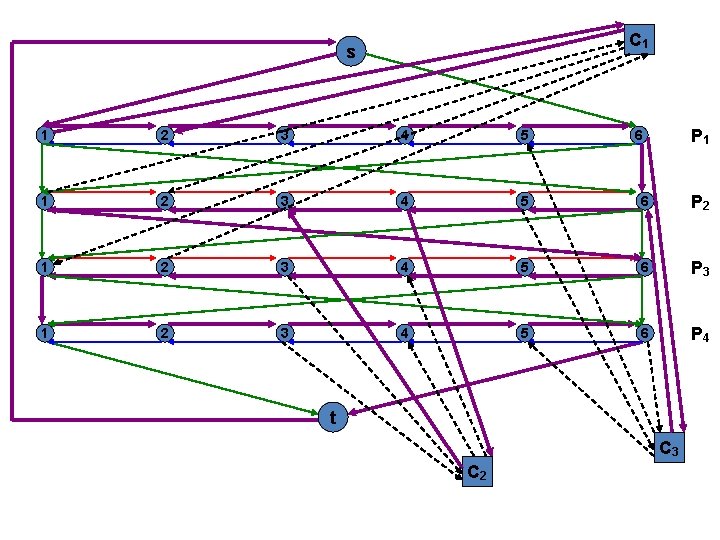
C 1 s P 1 1 2 3 4 5 6 P 2 1 2 3 4 5 6 P 3 1 2 3 4 5 6 P 4 t C 3 C 2

Hamiltonian Cycle Problem Part II Given A Hamiltonian cycle in G. Observe that if the cycle enters a node cj on an edge from vi, 2 j-1 it must depart on an edge to vi, 2 j. Why?

Hamiltonian Cycle Problem Because otherwise, the tour will not be able to cover this node while still maintaining the Hamiltonian property Similarly, if the path enters from vi, 2 j, it has to d e p a r t i m m e d i a t e l y t o vi , 2 j - 1.

Hamiltonian Cycle Problem However, in some situations it may so happen that the path enters cj from the first (or last) node of Pi and departs at the first (or last) node of Pi+1. In either case the following holds true: The nodes immediately before and after any cj in the cycle are joined by an edge in G, say e. Let us consider the following Hamiltonian cycle given on our graph

C 1 s P 1 1 2 3 4 5 6 P 2 1 2 3 4 5 6 P 3 1 2 3 4 5 6 P 4 t C 3 C 2

Hamiltonian Cycle Problem Obtain a Hamiltonian cycle on the subgraph G – {c 1, ……ck} by removing cj a n d a d d i n g ‘e’ as shown below

C 1 s P 1 1 2 3 4 5 6 P 2 1 2 3 4 5 6 P 3 1 2 3 4 5 6 P 4 t C 3 C 2

Hamiltonian Cycle Problem We now use this new cycle on the subgraph to obtain the truth assignments for the 3 -SAT instance. I f i t t r a v e r s e s P i l e f t t o r i g h t , s e t xi = 1 , e l s e set xi = 0. We therefore get the following assignments: x 1 = 1 x 2 = 0 x 3 = 0 x 4 = 1

Hamiltonian Cycle Problem Can we claim that the assignment thus determined would satisfy all clauses. YES ! Since the larger cycle visited each clause node cj, at least one Pi was traversed in the right direction relative to the node cj

Acknowledgements • BIG Thanks to Sonika Arora