MESURES ET INSTRUMENTATION ERREURS INCERTITUDES DE MESURE I

MESURES ET INSTRUMENTATION : ERREURS / INCERTITUDES DE MESURE I N La métrologie (science de la mesure) rassemble les connaissances permettant de donner un sens à la mesure. T Elle permet: R O D U C T I O N La caractérisation quantitative des propriétés d’un objet; La comparaison d’une même propriété pour deux objets; La confrontation entre la théorie et l’expérience; La validation ou non du modèle retenu…. Tout cela passe par l’attribution d’une valeur numérique aux grandeurs intervenant. À chaque changement de définition des unités fondamentales correspond une précision accrue : le critère retenu dans le choix des unités de base est celui de l’exactitude maximale avec laquelle unité peut être réalisée expérimentalement sous la forme d’un étalon.

Exemple : TEMPS La seconde était avant 1960 définie comme la fraction 1/ 86164, 09055 de la durée de la rotation propre de la Terre. Or la Terre ralentit ! Meilleure horloge : horloges atomiques (cf définition de 1983) dont on peut penser que la période est une vraie période (invariable dans le temps). Des résultats d’observations sont alors utilisables en tout temps. Attention! L’utilisateur courant ne doit pas être perturbé par le changement : la « taille » de l’unité reste la même. Exemple: LONGUEUR La définition initiale de 1790 posait 1 km = longueur d’un méridien terrestre / 40000. La définition actuelle du mètre revient à fixer la vitesse de la lumière dans le vide à 299792458 m/s. Avec cette définition, la longueur d’un méridien vaut 40008, 08 km.

On cherche à mesurer une grandeur X (le mesurande). La mesure (ou mesurage) consiste à attribuer une valeur numérique x à cette grandeur. D É F I N I T I O N S Exemple: on mesure avec un ohmmètre la résistance R d’un conducteur ohmique, l’ohmmètre affiche la valeur numérique 1, 54 k Pour plusieurs mesures d’une même grandeur X, dans les mêmes conditions de répétabilité, les résultats xi se répartissent autour d’une valeur moyenne Ceci est dû aux petites variations aléatoires des nombreuses grandeurs influençant la mesure Exemple: les variations de température de chaque composant électronique de l’ohmmètre. Il en résulte une incertitude sur la mesure de la grandeur. On définit l’erreur aléatoire:

Le résultat d’une mesure est précis lorsque les indications données par l’instrument de mesure restent très voisines pour le même mesurande dans les mêmes conditions. L’instrument est alors caractérisé par une bonne fidélité (les résultats qu’il donne s’écartent peu de la valeur moyenne). Le résultat de la mesure est exact s’il est proche des valeurs établies avec un appareillage de référence, sensé donner la valeur vraie xvrai de X. l’instrument est alors caractérisé par sa justesse. Un instrument dont le zéro est mal réglé peut donner un résultat précis…mais faux. L’erreur commise lorsque l’on fait un très grand nombre de mesures est appelée erreur systématique : La valeur moyenne de la série de mesure est systématiquement plus petite ou plus grande que la valeur vraie…

Lorsque l’on ne fait qu’une mesure, on commet une erreur de mesure, somme de l’erreur aléatoire et de l’erreur systématique : On peut s’affranchir de l’erreur systématique grâce à de bonnes connaissances en Physique et la construction soignée d’appareils de mesure, alors que l’erreur aléatoire est inévitable. On suppose par la suite:

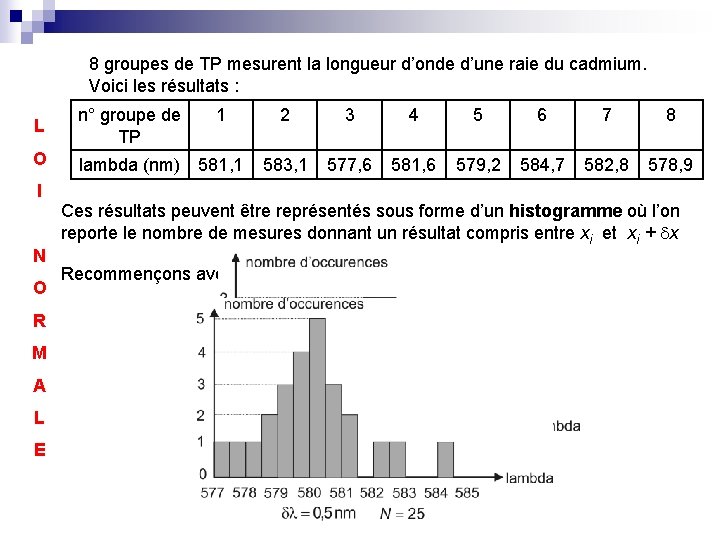
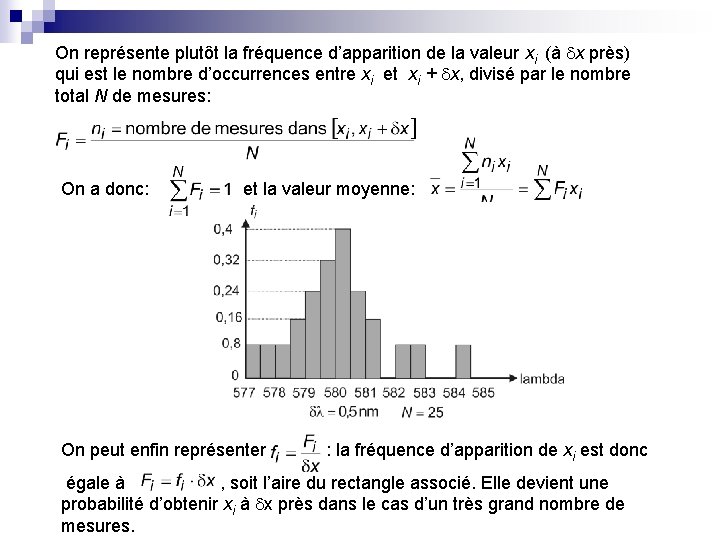
8 groupes de TP mesurent la longueur d’onde d’une raie du cadmium. Voici les résultats : L n° groupe de TP 1 2 3 4 5 6 7 8 O lambda (nm) 581, 1 583, 1 577, 6 581, 6 579, 2 584, 7 582, 8 578, 9 I N O R M A L E Ces résultats peuvent être représentés sous forme d’un histogramme où l’on reporte le nombre de mesures donnant un résultat compris entre xi et xi + x Recommençons avec 25 groupes et des intervalles plus fins :

On représente plutôt la fréquence d’apparition de la valeur xi (à x près) qui est le nombre d’occurrences entre xi et xi + x, divisé par le nombre total N de mesures: On a donc: et la valeur moyenne: On peut enfin représenter : la fréquence d’apparition de xi est donc égale à , soit l’aire du rectangle associé. Elle devient une probabilité d’obtenir xi à x près dans le cas d’un très grand nombre de mesures.

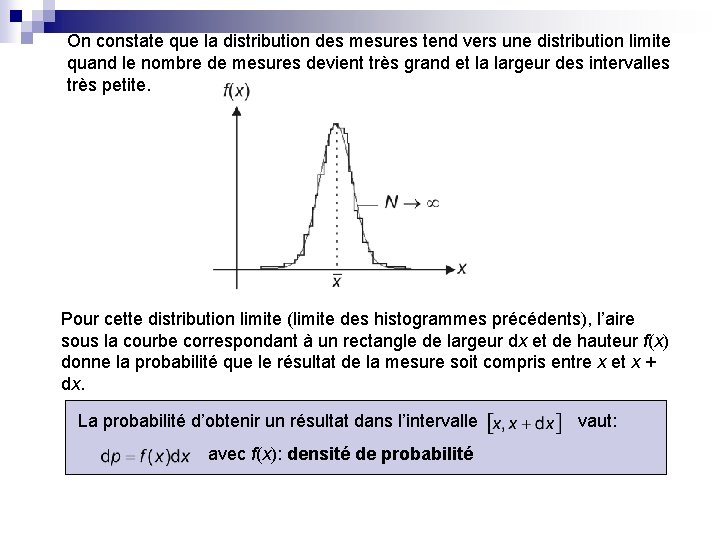
On constate que la distribution des mesures tend vers une distribution limite quand le nombre de mesures devient très grand et la largeur des intervalles très petite. Pour cette distribution limite (limite des histogrammes précédents), l’aire sous la courbe correspondant à un rectangle de largeur dx et de hauteur f(x) donne la probabilité que le résultat de la mesure soit compris entre x et x + dx. La probabilité d’obtenir un résultat dans l’intervalle avec f(x): densité de probabilité vaut:

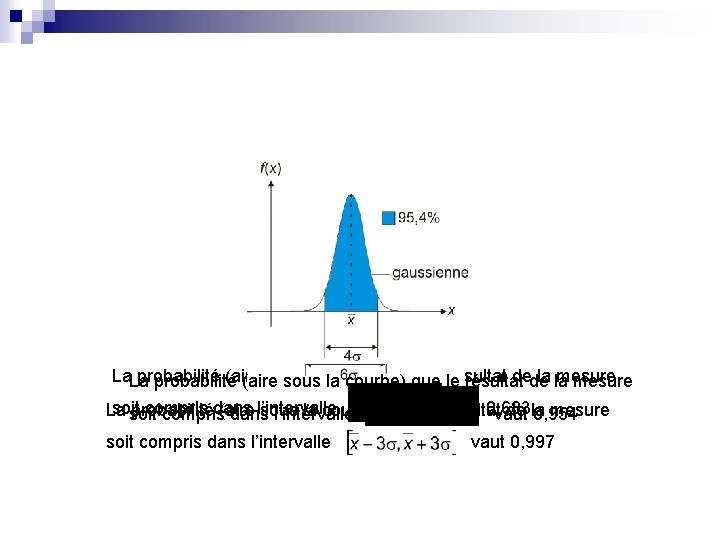
Probabilité que le résultat de la mesure soit compris entre les valeurs x 1 et x 2 : vaut évidemment 1 si et Moyenne de la distribution: On définit l’écart type de la distribution : mesurant la dispersion des résultats autour de la moyenne. On a C’est l’analogue de la valeur efficace d’un signal alternatif, d’autant plus grande que le signal s’écarte de 0.

Le cas le plus fréquent est celui où l’erreur aléatoire suit la loi normale (gaussienne) : La distribution limite précédente est une courbe en cloche centrée sur la valeur moyenne est l’écart type de la distribution mesurant la dispersion des résultats autour de la moyenne Un théorème mathématique (théorème central limite) établit l’équation de cette distribution limite dans le cas où de nombreux facteurs indépendants viennent légèrement influencer la mesure. Remarque: la fonction gaussienne décroît suffisamment rapidement lorsque x s’écarte de pour que l’on étende les bornes d’intégration de à même si la grandeur X est par exemple une grandeur positive.

La. La probabilité (aire sous la la courbe) que le le résultat dede la la mesure probabilité (aire sous courbe) que résultat mesure soit compris dans l’intervalle vaut 0, 683 La probabilité (aire sous la courbe) que le résultat de la mesure soit compris dans l’intervalle vaut 0, 954 soit compris dans l’intervalle vaut 0, 997

Par la suite on donnera des intervalles de confiance à 95% sous la forme avec une « incertitude élargie » c’est-à-dire 2 fois « l’incertitude-type » L’écart type mesure donc la largeur de la distribution et le résultat de l’expérience est donné par convention sous la forme. Il ne faut pas interpréter 2 comme la valeur maximale de l’incertitude mais comme une donnée probabiliste : on a une probabilité de 95 % que le résultat de la mesure de la grandeur X se trouve dans l’intervalle ,

ÉVALUATION DES INCERTITUDES PAR DES MÉTHODES STATISTIQUES (DE TYPE A): LOIS DE STUDENT Comme en pratique N est fini, la valeur vraie reste inconnue : différentes séries de mesures portant sur la même grandeur vont donner des valeurs moyenne différentes (réparties autour de la valeur de la distribution) et des écarts types différents répartis autour de . On montre (cf annexe) que l’écart-type sur la moyenne est lié à l’écart-type de la distribution par la formule On retrouve ainsi que valeur vraie . : on n’aurait aucune incertitude sur la avec un nombre infini de mesures…

En réalité, cette incertitude décroît « lentement » : en faisant 100 fois plus de mesures, on ne gagne qu’un facteur 10 pour l’incertitude. De toutes façons, la réalisation d’un très grand nombre de mesures est coûteuse en temps et en argent. Dans la pratique, on ne réalise qu’un petit nombre de mesures (très petit dans le cas de T. P où souvent N est inférieur à 10). Dans le cas où l’on a réalisé N mesures de la même grandeur donnant des résultats , on montre que les meilleurs estimateurs de et de sont respectivement (cf annexe): qui s’identifient bien à et quand Pour N « petit » , il faut tenir compte d’un terme correctif l’incertitude élargie à 95% sur : dans

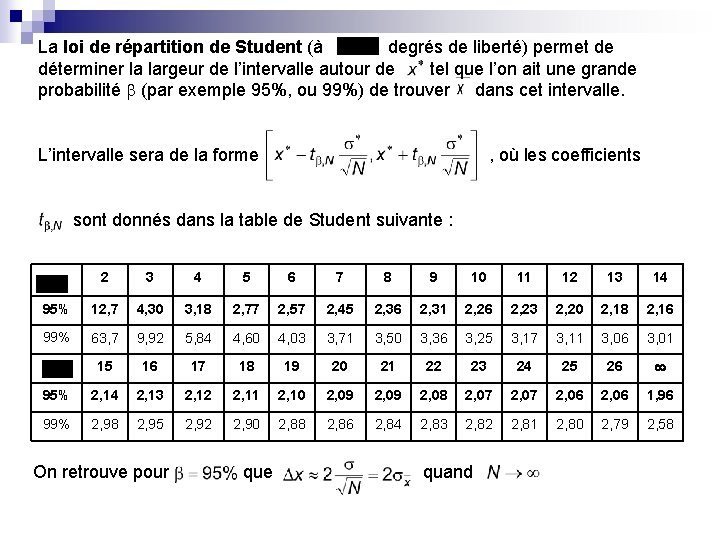
La loi de répartition de Student (à degrés de liberté) permet de déterminer la largeur de l’intervalle autour de tel que l’on ait une grande probabilité (par exemple 95%, ou 99%) de trouver dans cet intervalle. L’intervalle sera de la forme , où les coefficients sont donnés dans la table de Student suivante : 2 3 4 5 6 7 8 9 10 11 12 13 14 95% 12, 7 4, 30 3, 18 2, 77 2, 57 2, 45 2, 36 2, 31 2, 26 2, 23 2, 20 2, 18 2, 16 99% 63, 7 9, 92 5, 84 4, 60 4, 03 3, 71 3, 50 3, 36 3, 25 3, 17 3, 11 3, 06 3, 01 15 16 17 18 19 20 21 22 23 24 25 26 95% 2, 14 2, 13 2, 12 2, 11 2, 10 2, 09 2, 08 2, 07 2, 06 1, 96 99% 2, 98 2, 95 2, 92 2, 90 2, 88 2, 86 2, 84 2, 83 2, 82 2, 81 2, 80 2, 79 2, 58 On retrouve pour que quand

Exemple : Le dosage en ions d’une même solution est réalisé simultanément par 9 groupes d’élèves, avec les résultats suivants (en ) pour groupe 1 2 3 4 5 6 7 8 9 résultat 1, 024 1, 028 0, 975 1, 031 0, 854 1, 100 0, 921 0, 945 0, 821 Intervalle de confiance à 95% : On lit dans les tables de Student On en déduit et

ÉVALUATION DES INCERTITUDES SUR UNE MESURE UNIQUE (DE TYPE B) Quelques règles simples permettent de donner les intervalles de confiance à 95% : (1) On utilise un appareil de mesure Le plus souvent, le constructeur fournit sans autre information une incertitude « constructeur » . Cette information est à prendre dans le sens : on est « à peu près sûr » de trouver la valeur vraie dans un intervalle de largeur Le bureau international des poids et mesures (B. I. P. M) préconise alors de modéliser cette information par une densité de probabilité uniforme pour l’intervalle: et nulle hors de cet intervalle. On en déduit alors (cf annexe) que l’incertitude-type vaut Et que l’incertitude élargie à 95% vaut

(1. 1) Cas d’un appareil analogique à aiguille (en voie d’extinction) La classe d’un appareil (à ne pas confondre avec la classe d’isolation) donne l’incertitude relative pour une mesure égale au calibre. Il faut lui rajouter l’incertitude de lecture que l’on prend égale à une demi-graduation. Exemple 1 : L’aiguille d’un ampèremètre analogique de classe 1 se stabilise au voisinage de la 83 ème graduation (sur 100) sur le calibre 200 m. A. On en déduit et On verra que l’on présente le résultat sous la forme : (1. 2) Cas d’un appareil numérique à affichage digital La précision d’un appareil donne l’incertitude relative. Attention : elle dépend du calibre (lire la notice). Il faut lui rajouter l’incertitude de 1 ou 2 « digits » , c’est-à-dire sur le dernier chiffre affiché.

Exemple 2 : On lit une intensité de 143, 2 m. A sur un ampèremètre numérique. Le constructeur donne une incertitude relative de 0, 5% sur la calibre utilisé (200 m. A) à laquelle il faut rajouter une incertitude de 1 digit. On en déduit On verra que l’on présente le résultat sous la forme : (2) On effectue une lecture directe pour une plage de valeurs correspondant aux critères de l’expérimentateur (par exemple, une plage de positions d’une lentille sur un banc optique telle que l’image d’un objet sur un écran à une distance fixe de l’objet soit vue nette) : on prend et

PRÉSENTATION DES RÉSULTATS Chiffres significatifs Ce sont tous les chiffres présents dans le nombre présenté. Les zéros placés en tête du nombre ne sont pas significatifs. Exemples : 350 : 3 chiffres significatifs : 2 chiffres significatifs : 3 chiffres significatifs Chiffres significatifs et précision. Si les incertitudes ne sont pas données, on considère par convention que le dernier chiffre significatif est connu à. signifie que

Lorsque l’on présente le résultat d’un calcul, il faut prendre en compte le nombre de chiffres significatifs des données : (règles simplifiées) pour une addition (ou une soustraction), le résultat ne peut pas avoir plus de décimales que la donnée qui en a le moins. Exemple : et pas 1496, 797 pour une multiplication (ou une division), le résultat ne peut pas avoir plus de chiffres significatifs que la donnée qui en a le moins. Exemple : et pas 3227, 23935 Présentation des résultats Les incertitudes étant elles-mêmes entachées d’incertitudes : (règles simplifiées) on ne conservera sauf cas particulier qu’un seul chiffre significatif pour l’incertitude correspondant à un niveau de confiance de 95%. Pour l’estimation de la grandeur mesurée, on prendra comme dernier chiffre significatif, celui de même position que celui de l’incertitude.

Exemple 1 : on lit sur un conducteur ohmique la couleur des bagues : marron (1), noir (0), rouge (2), or (5%). On en déduit : Exemple 2 : On lit sur un vernier un angle compris entre 152° 27’ et 152° 28’. On a donc : Exemple 3 : une source lumineuse étant à l’infini, un élève mesure la distance focale d’une lentille convergente en cherchant à quelle distance il faut placer un écran de la lentille pour trouver une image nette. Il considère que l’image est nette sur l’intervalle de distances On en déduit :

PROPAGATION DES INCERTITUDES La mesure d’une grandeur X fournit un résultat avec une incertitude Si la grandeur X n’est pas directement accessible par la mesure mais liée à des mesures indépendantes de deux grandeurs elles- mêmes indépendantes et dont les valeurs mesurées sont (avec une incertitude ): On montre (cf annexe) alors que l’on a : (avec une incertitude ) et

Cette relation peut se généraliser au cas où X dépend de plus de deux variables. Appliquons cette relation à des cas simples : Autrefois, on ne demandait qu’une majoration de l’incertitude : Par exemple, en prenant la différentielle logarithmique de. on obtient : qui entraîne en majorant l’incertitude : est l’incertitude relative sur X

À titre d’exemple, calculons l’incertitude relative sur le facteur de qualité Q et sur la pulsation propre d’un circuit RLC série, R, L et C étant connus avec une incertitude relative de 0, 5% : Comparons avec la majoration : La majoration donne souvent un résultat exagéré pour les incertitudes, avec perte d’information sur l’intervalle de confiance.

Attention! Grandeurs non indépendantes…. Comme le facteur de qualité s’écrit également utiliser l’incertitude sur on peut penser à qui a été calculée précédemment : Ce résultat, différent du précédent, est faux car surévalué : les trois variables L, et R ne sont pas indépendantes du point de vue des incertitudes. De même, si l’on utilise le même appareil pour mesurer deux grandeurs homogènes indépendantes et , les mesures ne sont pas indépendantes si bien que l’on ne peut pas utiliser pour calculer l’incertitude sur la somme ou la différence entre ces deux grandeurs. On se contente souvent d’une majoration en cas de doute sur l’indépendance des mesures.