Lanalyse de variance mesures rptes ANOVA mesures rptes

L’analyse de variance à mesures répétées

ANOVA à mesures répétées Utilité: Lorsque des participants sont mesurés à plusieurs reprises (2 et +)

Exemple L’effet d’une technique de relaxation sur les migraines. groupe 1: semaine 1 groupe 2: semaine 2 groupe 3: semaine 3 groupe 4: semaine 4 groupe 5: semaine 5 Hypothèses:

Variance En ANOVA simple, la séparation des sommes de carrés (variation) est faite selon: Variation totale = inter groupe + intra groupe On utilisant les même sujets on arrive à séparer la variation intra groupe en variation inter sujets et en variation intra sujets. Par conséquent, la nouvelle séparation est alors : Variation totale = inter groupe + (inter sujets + intra sujets)

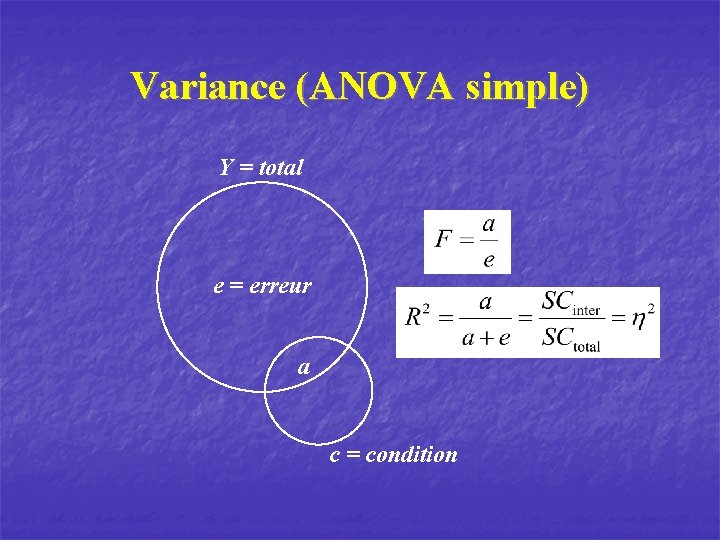
Variance (ANOVA simple) Y = total e = erreur a c = condition

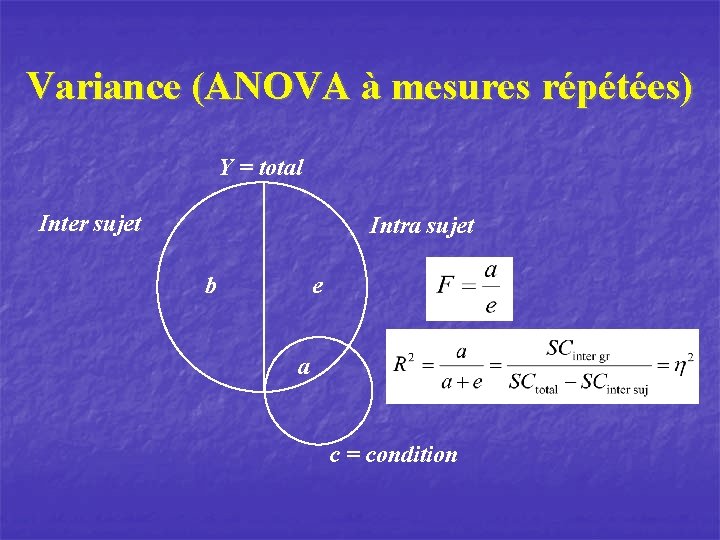
Variance (ANOVA à mesures répétées) Y = total Inter sujet Intra sujet b e a c = condition

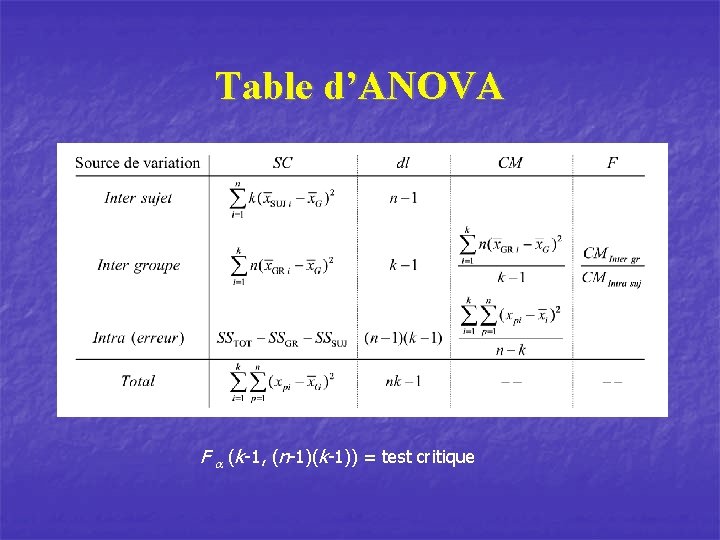
Table d’ANOVA F a (k-1, (n-1)(k-1)) = test critique

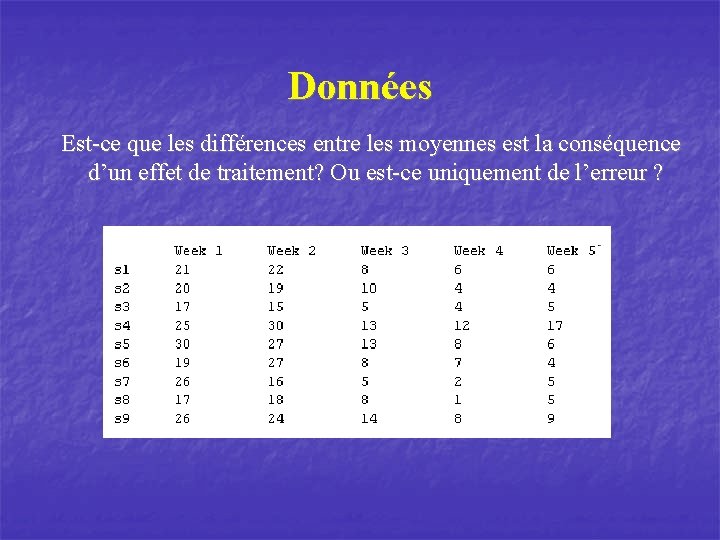
Données Est-ce que les différences entre les moyennes est la conséquence d’un effet de traitement? Ou est-ce uniquement de l’erreur ?

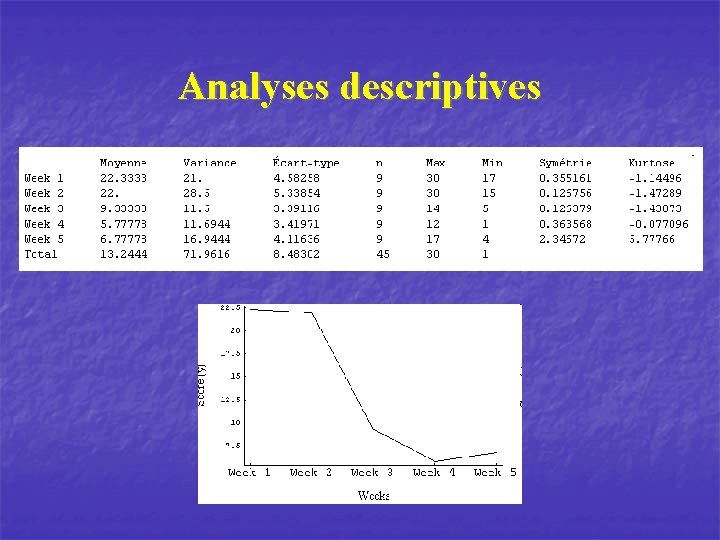
Analyses descriptives

Postulats n n Assignation au hasard Symétrie composée: Les variances sont similaires (homogénéité des variances) et les covariances sont similaires (homogénéité des covariances) Matrice variances/covariances

Postulats Symétrie composée (suite) n n n Si le postulat de symétrie composée n’est pas respecté, il faut voir la sphéricité. Si le postulat de symétrie composée est rencontré alors la sphéricité est aussi rencontré (le contraire n’est pas vraie). Sphéricité: les variances différences entre chacun des traitements sont similaires.

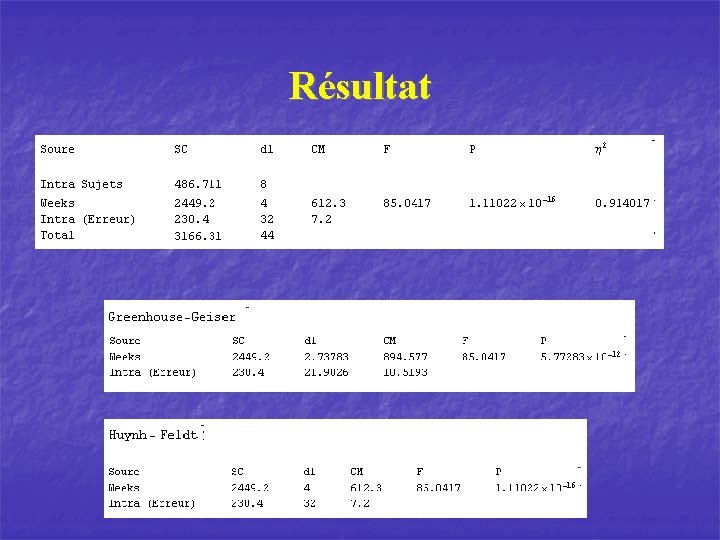
Postulats Sphéricité (suite) n n Il existe le test de Mauchly pour tester la sphéricité, cependant ce test n’est pas très robuste. Par conséquent, il vaut mieux utiliser les corrections. n n Greenhouse-Geiser Huynh-Feldt Donc, au lieu d’utiliser un F avec dl 1= k-1 et dl 2=(n-1)(k-1) on va utiliser un F avec dl 1=(k-1)e et dl 2=(n-1)(k-1)e. Où e (epsilon) est donné par les différentes corrections. (note: si e<0. 7, le postulat de sphéricité n’est pas rencontré)

Résultat

Résultat

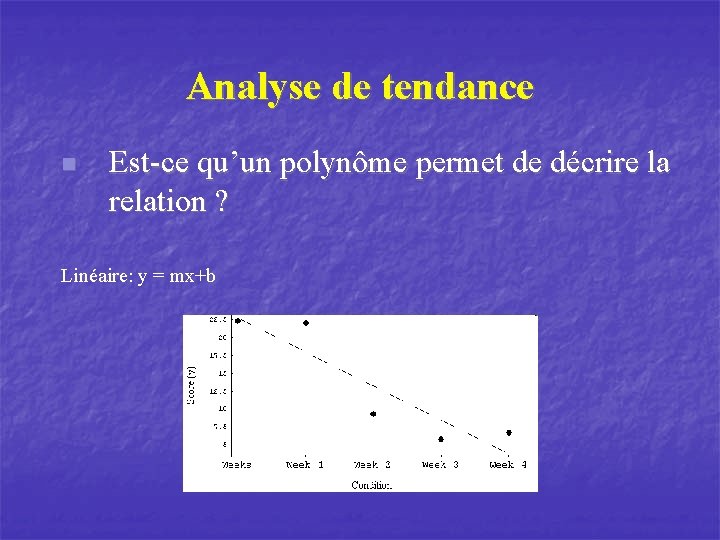
Analyse de tendance n Est-ce qu’un polynôme permet de décrire la relation ? Linéaire: y = mx+b

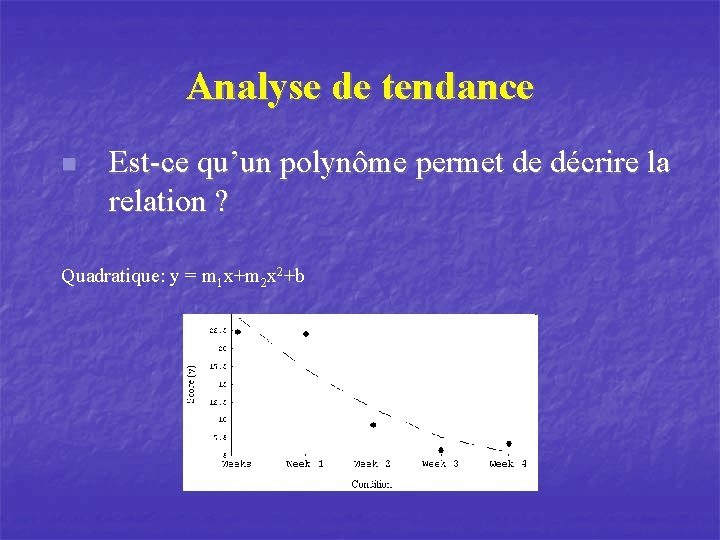
Analyse de tendance n Est-ce qu’un polynôme permet de décrire la relation ? Quadratique: y = m 1 x+m 2 x 2+b

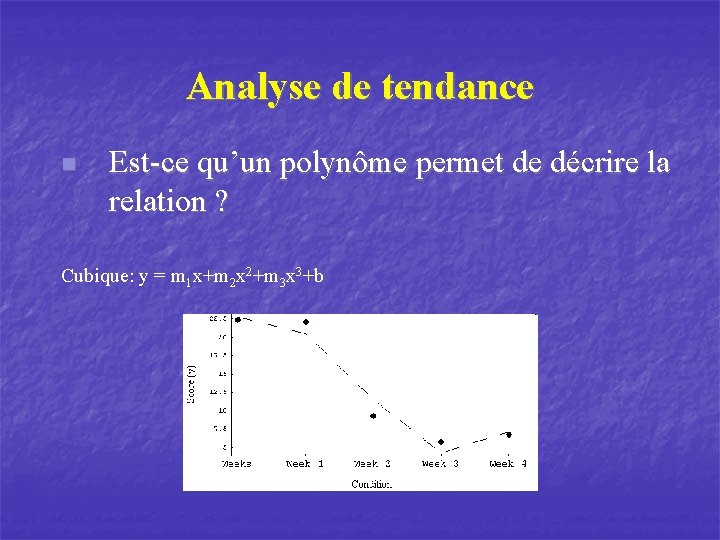
Analyse de tendance n Est-ce qu’un polynôme permet de décrire la relation ? Cubique: y = m 1 x+m 2 x 2+m 3 x 3+b

Analyse des contrastes Comme d’habitude n n Si le nombre de contrastes est plus grand que k-1 Dunn/Sidák Bonferroni