Materily jsou ureny pro vuku matematiky 3 ronk

Materiály jsou určeny pro výuku matematiky: 3. ročník Učivo v elektronické podobě zpracovala Mgr. Iva Vrbová

KOMBINATORIKA

Motivační úloha Žáci jedou vlakem na výlet. V kupé pro osm cestujících chtějí tři žáci sedět ve směru jízdy, dva žáci proti směru jízdy a třem žákům je to jedno. Kolika způsoby se těchto osm žáků může usadit?

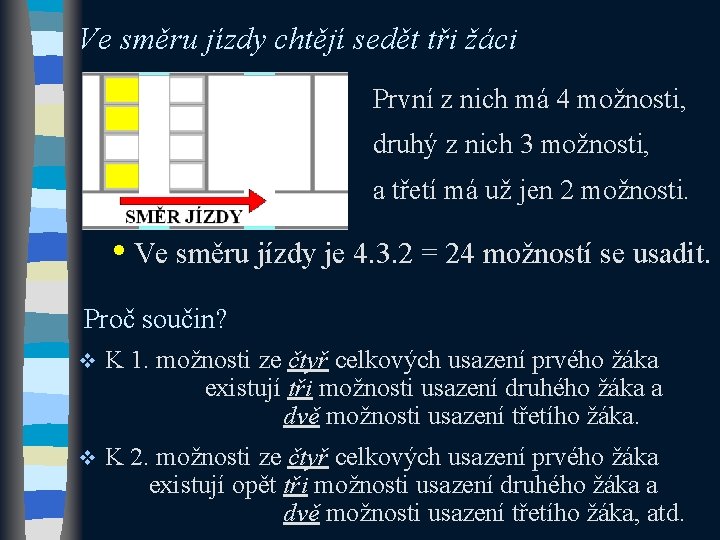
Ve směru jízdy chtějí sedět tři žáci První z nich má 4 možnosti, druhý z nich 3 možnosti, a třetí má už jen 2 možnosti. • Ve směru jízdy je 4. 3. 2 = 24 možností se usadit. Proč součin? v K 1. možnosti ze čtyř celkových usazení prvého žáka existují tři možnosti usazení druhého žáka a dvě možnosti usazení třetího žáka. v K 2. možnosti ze čtyř celkových usazení prvého žáka existují opět tři možnosti usazení druhého žáka a dvě možnosti usazení třetího žáka, atd.

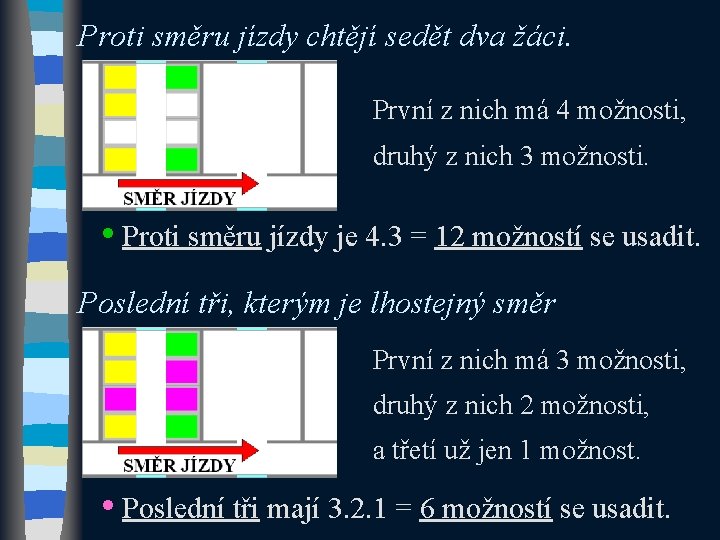
Proti směru jízdy chtějí sedět dva žáci. První z nich má 4 možnosti, druhý z nich 3 možnosti. • Proti směru jízdy je 4. 3 = 12 možností se usadit. Poslední tři, kterým je lhostejný směr První z nich má 3 možnosti, druhý z nich 2 možnosti, a třetí už jen 1 možnost. • Poslední tři mají 3. 2. 1 = 6 možností se usadit.

• • • Ve směru jízdy: 24 možností. Proti směru jízdy: 12 možností. Ve směru či proti směru jízdy: 6 možností. Celkový počet možností – výsledek • k 1. možnosti z prvních 24 existuje 12 druhých možností, 6 třetích možností, • k 2. možnosti z prvních 24 existuje také 12 druhých možností, 6 třetích možností, . . . • opět použijeme (vcelku logicky) pravidlo součinu a vypočteme: 24. 12. 6 = 1 728 Žáci se mohou usadit 1 728 způsoby.

Kombinatorika je n část matematiky, která se zabývá seskupováním prvků z určité konečné množiny Můžeme například spočítat, kolika způsoby lze vybrat tři reprezentanty třídy 3 OA, kteří. . . n nauka o skupinách

Kombinatorika a její vývoj n Různé kombinatorické úlohy řešili již starořečtí či indičtí matematici. n K oddělení od obecné matematiky a k utváření jako samostatné vědecké disciplíny došlo v 16. a 17. století. Důvod byl velmi prozaický. Byly to především hazardní hry. n Dnes je kombinatorika součástí matematiky, která studuje vlastnosti konečných množin. Její aplikace pomáhají řešit i důležité problémy ekonomické.

Úkol kombinatoriky n Vytvořit na základě určitého předpisu všechny možné skupiny prvků z předem dané konečné množiny a především určit počet všech těchto skupin. n Úlohy kombinatoriky budeme tedy řešit v oboru čísel celých nezáporných: N 0 = {0; 1; 2; 3; 4; . . . }

Značení prvků n Předem daná konečná množina, z níž skupiny tvoříme, má n prvků. n Skupinu, která obsahuje k prvků, nazýváme skupinou k-té třídy. • například: Tvoříme-li dvojčlenné skupiny z 10 lidí, pak n = 10, k = 2. Tvoříme-li trikolóry z pěti různých barev, pak n = 5, k = 3.

Prvky ve skupině Vyskytuje-li se vybraný prvek ve skupině a) pouze jednou, mluvíme o skupinách bez opakování • vybíráme-li skupiny z lidí b) několikrát (maximálně k-krát), mluvíme o skupinách s opakováním • například: vždy, když vybíráme skupiny z cifer a je uvedeno, že opakovat lze

Požadavek na předpis skupiny Jestliže na pořadí prvků ve skupině 1. záleží, 2. nezáleží,

Kombinator. pravidlo součinu n Zadání: U stánku nabízejí tři druhy zmrzliny a dvě polevy. Kolik různých zmrzlin s polevou lze vytvořit, jestliže nechceme míchat více druhů ani více polev? n Řešení: Tvoříme jeden kornout (1 skupinu). Do kornoutu vybíráme 1 zmrzlinu ze všech zmrzlin (1. podskupina) a zvlášť 1 polevu ze všech polev (2. podskupina). n Odpověď: Můžeme si pochutnat celkem na 3. 2 = 6 druzích zmrzlin s polevou.

KOMBINATORICKÉ PRAVIDLO SOUČINU Počet všech uspořádaných k-tic, jejichž první člen lze vybrat n 1 způsoby, druhý člen po výběru prvního členu n 2 způsoby atd. až ktý člen po výběru všech předcházejících členů nk způsoby, je roven

Kdy volíme KOMB. PRAV. SOUČINU n Tvoříme-li JEDNU skupinu, která je složena z rozlišných „nesourodých“ podskupin. n Například: Tvoříme-li • taneční pár: Ø 1. podskup. = ženy, 2. podskup. = muži • SPZ automobilu: Ø 1. podskup. = písmena, 2. podskup. = čísla

KOMB. PRAVIDLO SOUČINU – příklad n Zadání: Určete, kolik můžeme vytvořit různých tanečních párů z 5 dívek a 7 chlapců. Řešení: Tvoříme jeden taneční pár (1 skupinu). Pár je tvořen 1 dívkou (1. podskupina) a 1 chlapcem (2. podskupina). n Odpověď: Celkem můžeme vytvořit 35 (=7. 5) různých tanečních párů.

Kolik různých optických signálů je možno dát vytahováním 5 různých barevných vlajek, je-li vždy všech pět vlajek nahoře? [120]

Osm studujících si slíbilo, že si pošlou vzájemně pohlednice z prázdninových cest. Kolik pohlednic bylo rozesláno? [56]

O Vánocích si deset přátel vzájemně předalo dárky. Kolik dárků bylo celkem předáno? [90] Dřívější SPZ automobilu byla tvořena třemi písmeny a čtyřmi čísly, např. ABC 1234. Určete kolik těchto SPZ bylo možné vytvořit, bereme-li v úvahu 24 písmen. [138 240 000]

Kolika způsoby lze rozdělit 8 účastníků finále na 100 m do osmi drah? [40 320]

Jsou dány cifry 1; 2; 3; 4; 5. Cifry nelze opakovat. Kolik je možno vytvořit z těchto cifer čísel, která jsou a) pětimístná, sudá, b) pětimístná, končící dvojčíslím 21, c) pětimístná, menší než 30 000, d) trojmístná, lichá, e) čtyřmístná, větší než 2 000, f) čtyřmístná, začínající cifrou 2, g) čtyřmístná, sudá nebo končící cifrou 3, h) dvojmístná nebo trojmístná. [a) 48, b) 6, c) 48, d) 36, e) 96, f) 24, g) 72, h) 80]

Jsou dány cifry 0; 1; 2; 3; 4. Cifry nelze opakovat. Kolik je možno vytvořit z těchto cifer čísel, která jsou (úkoly minulé úlohy) a) pětimístná, sudá, b) pětimístná, končící dvojčíslím 21, c) pětimístná, menší než 30 000, d) trojmístná, lichá, e) čtyřmístná, větší než 2 000, f) čtyřmístná, začínající cifrou 2, g) čtyřmístná, sudá nebo končící cifrou 3, h) dvojmístná nebo trojmístná. [a) 60, b) 4, c) 48, d) 18, e) 72, f) 24, g) 78, h) 64]