Materily jsou ureny pro vuku matematiky Uivo v

Materiály jsou určeny pro výuku matematiky: Učivo v elektronické podobě zpracovala Mgr. Iva Vrbová (s laskavým svolením i pro výuku SPŠ a OA Bruntál)

KOMPLEXNÍ ČÍSLA (KČ) Číselný obor, který se označuje Zavedení oboru C C

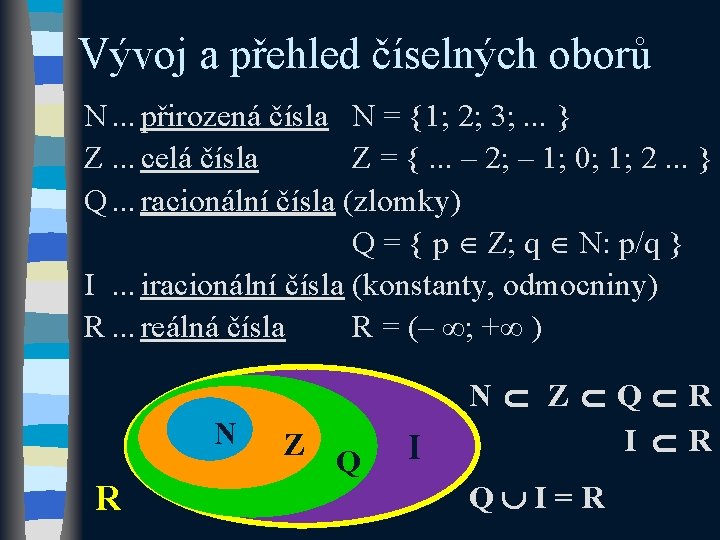
Vývoj a přehled číselných oborů N. . . přirozená čísla N = {1; 2; 3; . . . } Z. . . celá čísla Z = {. . . – 2; – 1; 0; 1; 2. . . } Q. . . racionální čísla (zlomky) Q = { p Z; q N: p/q } I. . . iracionální čísla (konstanty, odmocniny) R. . . reálná čísla R = (– ∞; +∞ ) N R Z Q I N Z Q R I R Q I=R

Diskriminant kvadratické rovnice: n V kvadratické rovnici vypočteme hodnotu výrazu, který řídí počet kořenů rovnice (diskriminant): 1) diskriminant je kladný, D > 0 • rovnice má 2 různé reálné kořeny 2) diskriminant je nulový, D = 0 • rovnice má 1 reálný kořen 3) diskriminant je záporný, D < 0 • rovnice nemá reálný kořen

D = (– 10)2 – 4. 1. 29 = 100 – 116 = – 16 < 0 Þ rovnice nemá v oboru reálných čísel řešení Þ Hledáme jiný početní postup a nový číselný obor, ve kterém bychom řešení nalezli: 1. vyjdeme z nejjednodušší rovnice tohoto typu (rovnice nemá v R řešení): 2. předpokládáme, že jejím kořenem je jisté číslo, které nazveme imaginární jednotkou: 3. uplatníme předpoklad a dosadíme:

Závěr: Řešením kvadratických rovnic, jejichž diskriminant je záporný, budou komplexní čísla.

Zápis komplexní čísla KČ zapisujeme dvěma způsoby a tudíž používáme • tvar algebraický, • tvar goniometrický.

Algebraický tvar komplexního čísla

Algebraický tvar (AT) se nazývá zápis: n , kde Ø a. . . KČ (a C ) Ø a 1. . . reálná část KČ a (a 1 R ) Ø a 2. . . imaginární část KČ a (a 2 R ) Ø i …. imaginární jednotka poznámka: slova latinského původu překládáme • komplexní = složené • imaginární = pomyslné, zdánlivé, neskutečné

Druhy komplexních čísel n KČ imaginární : a=5 -3 i n KČ ryze imaginární – chybí reálná část: a=5 i n n KČ reálná – chybí imaginární část: a=-3 tedy: R C

Znázornění komplexní čísla KČ znázorňujeme jako • body Gaussovy roviny, • vektory Gaussovy roviny. Gaussova rovina, 0(x, y) • ortogonální soustava souřadných os x, y.

Znázornění KČ

reálná část imaginární část Obrazem KČ a = a 1 + a 2 i je v Gaussově rovině 0(x, y) bod A[a 1; a 2]. imaginární osa = y A = [a 1; a 2] a 2 0 a 1 x = reálná osa

KČ rozlišujeme a v AT zapisujeme: KČ reálná: a = a 1 a = 3; a = – 5; . . . a 1 R a 2 = 0 obrazy jsou body souřadné osy x KČ ryze imaginární: a = a 2 i a = – 2 i; a = 4 i; . . . a 1 = 0 a 2 R – {0} obrazy jsou body souřadné osy y KČ imaginární: a = a 1 + a 2 i a = 3 + i; a = 1 – 5 i; . . . a 1 R – {0} a 2 R – {0} obrazy jsou body, které neleží na souřadných osách

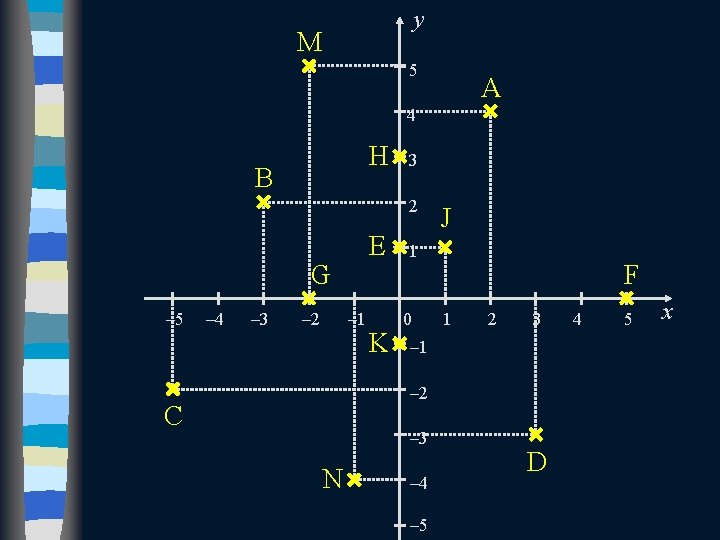
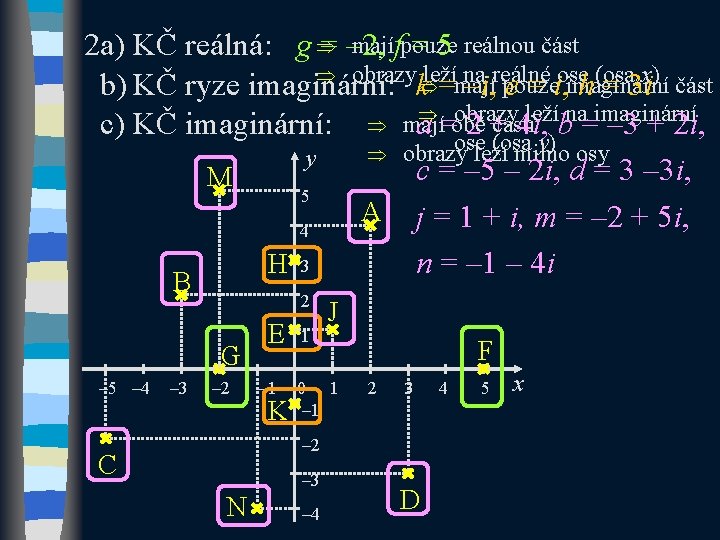
Příklad: 1) Sestrojte v Gaussově rovině obrazy KČ. 2) Vyberte, která ze zadaných KČ jsou a) reálná, b) ryze imaginární, c) imaginární.

y M 5 A 4 H B 3 2 E G – 5 – 4 – 3 – 2 – 1 K J 1 0 F 1 2 3 – 1 – 2 C – 3 N – 4 – 5 D 4 5 x

majífpouze 2 a) KČ reálná: g Þ= – 2, = 5 reálnou část Þ obrazy leží na reálné ose (osa x) b) KČ ryze imaginární: kÞ=mají –i, pouze e = i, imaginární h = 3 i část obrazy leží na imaginární části c) KČ imaginární: Þ mají aÞ =obě 2 + 4 i, b = – 3 + 2 i, oseleží (osa y) osy Þ obrazy mimo y c = – 5 – 2 i, d = 3 – 3 i, M 5 A j = 1 + i, m = – 2 + 5 i, 4 n = – 1 – 4 i H 3 B 2 G – 5 – 4 – 3 – 2 E – 1 K 1 J 0 1 – 1 F 2 3 – 2 C – 3 N – 4 D 4 5 x