MATEMATIKA 8 RONK RIEENIE LINERNYCH ROVNC A NEROVNC

MATEMATIKA 8. ROČNÍK RIEŠENIE LINEÁRNYCH ROVNÍC A NEROVNÍC

Riešenie lineárnych rovníc pomocou ekvivalentných úprav Čo už vieme: Rovnosť dvoch matematických výrazov s tou istou neznámou x upravíme na tvar : a. x = b, x je neznáma, a, b sú čísla, a 0. Číslom a je vynásobená neznáma, nazýva sa koeficient pri neznámej Riešenie (koreň) rovnice je číslo Takúto rovnicu nazývame lineárna rovnica (rovnica prvého stupňa) s jednou neznámou. Zisti, ktoré zo zápisov sú rovnice: a) 3 x – 6 = 2 x + x N b) 15 x +12 = 3. (4 x – 3) A c) – 7 x + 8 = - 7 x + 8 V rovnostiach a) a c) je po úprave a = 0 – teda nie sú rovnice N

6 / úl. 1. : a) 2 x + 5 x – 6 x = -2. 3 x =-6 lineárna rovnica s jednou neznámou 10 x – 10 x = 7 2 x = 2. 0, 5 – 1, 2 + 0, 6 : 3 2 x = 1 – 1, 2 + 0, 2 2 x = 0 lineárna rovnica s jednou neznámou 0 x = 0 0 x = 7 - taký zlomok neexistuje a neexistuje číslo, ktoré rovnosti vyhovuje – daná rovnosť nie je lineárna rovnica - taký zlomok neexistuje a existuje nekonečne veľa čísel, ktoré rovnosti vyhovujú –daná rovnosť nie je lineárna rovnica

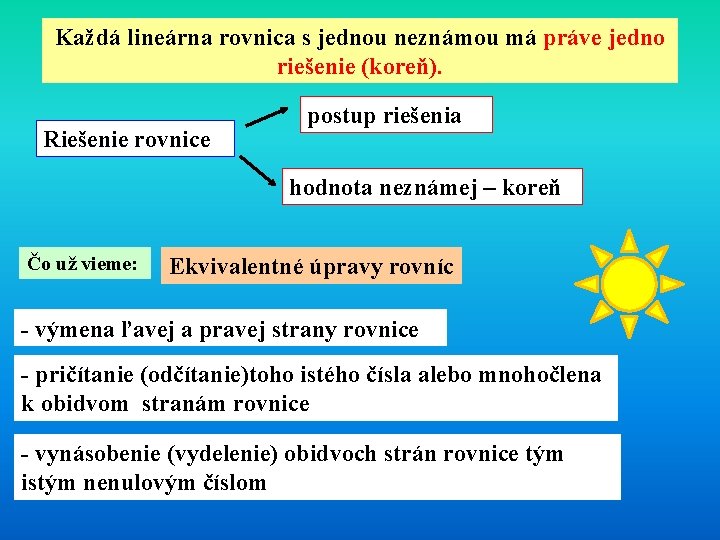
Každá lineárna rovnica s jednou neznámou má práve jedno riešenie (koreň). Riešenie rovnice postup riešenia hodnota neznámej – koreň Čo už vieme: Ekvivalentné úpravy rovníc - výmena ľavej a pravej strany rovnice - pričítanie (odčítanie)toho istého čísla alebo mnohočlena k obidvom stranám rovnice - vynásobenie (vydelenie) obidvoch strán rovnice tým istým nenulovým číslom

Rieš rovnice a doplň tabuľku: a) 2 x – (8 x – 1) – ( - x + 2) = 9 b) 2, 5 x – 3. (1, 5 x – 1) = 9 c) d) Koreň rovnice a) b) c) d) e) Ľ P e)

Vyjadrenie neznámej zo vzorca Vzorec upravíme ekvivalentnými úpravami tak, aby neznáma, ktorú máme vyjadriť, bola na ľavej strane a ostatné premenné na pravej strane rovnosti. Zo vzorca na výpočet obsahu obdĺžnika vyjadri stranu a. Zo vzorca na výpočet obsahu trojuholníka vyjadri výšku na stranu a. S=a. b = S /: b 2. S = a. va Obvod štvorca má dĺžku 48 cm. Aká je dĺžka jednej strany? Najskôr vyjadri zo vzorca, potom dosaď a vypočítaj o=4. a a=o: 4 o = 4. 12 a = 48 : 4 = 12 o = 48 cm

Slovné úlohy riešené lineárnymi rovnicami Text úlohy: Rozdeľ 130 orechov na 2 časti tak, aby menšia časť zväčšená 4 -krát sa rovnala väčšej časti zmenšenej 3 -krát. Rozbor úlohy: Menšia časť. . . . x, zväčšená 4 -krát. . . . 4. x Väčšia časť. . 130 – x, zmenšená 3 -krát. . . (130 – x): 3 = Zostavenie a riešenie rovnice: Skúška: Menšia č. . . 10, zväčšená 4 -krát. . . 40 Väčšia č. . 130 – 10=120, zmenš. 3 -krát=40 Odpoveď: Menšia časť je 10, väčšia časť je 120

Slovné úlohy o rovnomernom pohybe rýchlosť. . v; dráha. . s; čas. . t; s = v. t; Auto ide priemernou rýchlosťou 70 km/h, rýchlik má rýchlosť 21 m/s. Ktorý dopravný prostriedok ide rýchlejšie? 70 km/h = 70000 m/s 1 h = 60 min. = 3600 s auto 19, 44 m/s, rýchlik. . . . 21 m/s alebo 21 m/s = 21. 3600 m/h = 75600 m /h = 75, 6 km/h auto. . 70 km/h, rýchlik. . 75, 6 km/h Väčšiu rýchlosť má rýchlik.

3 480 km 27 / 14: 1. L – 6. 30 2. L – 7. 00 1. L. . . v 1 = ( x + 60) km/h , t 1 = 2, 5 hod. , s 1 = 2, 5 (x + 60) 2. L. . . v 2 = x km/h , s 2 = 2 x 2, 5 (x + 60 ) + 2 x = 3480 x = 740 Lietadlá sa míňajú 2000 km od prvého letiska. t 2 = 2 hod. , Sk. : s 1 = 2, 5 (740 + 60) = 2, 5. 800 = 2000 km s 2 = 2 x = 2. 740 = 1480 km Spolu : 3 480 km Dva objekty sa pohybujú po dráhe oproti sebe. Na dráhu vyrazia súčasne. Platí: Na dráhe sú rovnaký čas. Celková dráha, ktorú objekty prešli sa rovná súčtu jednotlivých dráh.

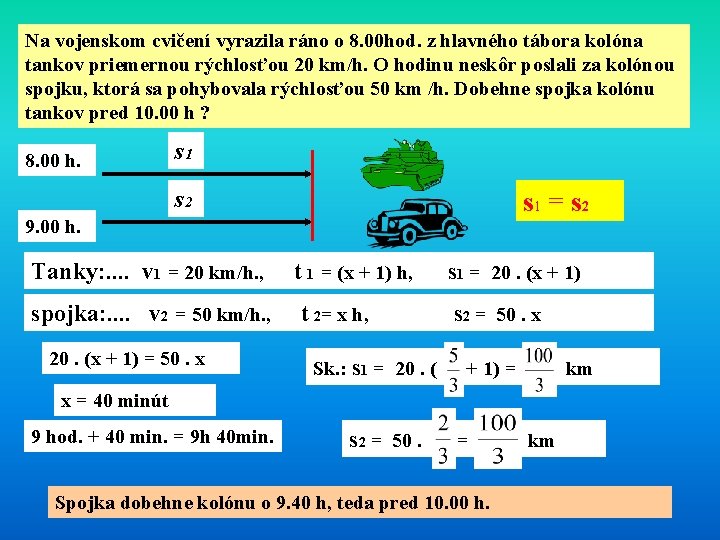
Na vojenskom cvičení vyrazila ráno o 8. 00 hod. z hlavného tábora kolóna tankov priemernou rýchlosťou 20 km/h. O hodinu neskôr poslali za kolónou spojku, ktorá sa pohybovala rýchlosťou 50 km /h. Dobehne spojka kolónu tankov pred 10. 00 h ? 8. 00 h. s 1 s 2 s 1 = s 2 9. 00 h. Tanky: . . v 1 = 20 km/h. , spojka: . . v 2 = 50 km/h. , 20. (x + 1) = 50. x t 1 = (x + 1) h, t 2= x h, Sk. : s 1 = 20. (x + 1) s 2 = 50. x + 1) = km x = 40 minút 9 hod. + 40 min. = 9 h 40 min. s 2 = 50. = Spojka dobehne kolónu o 9. 40 h, teda pred 10. 00 h. km

Dva objekty sa pohybujú za sebou, vyšli z toho istého miesta s časovým odstupom. Dráha, ktorú prešli po miesto stretnutia je rovnaká. Na trati sú mestá A a B vzdialené 42 km. Z mesta A vyjde chodec rýchlosťou 6 km /h opačným smerom, ako je B. O pol hodinu vyjde z B cyklista rýchlosťou 24 km/h. Za aký čas dobehne cyklista chodca a v akej vzdialenosti od B? A 42 km B Chodec: . . v 1 = 6 km/h. , cyklista: . . v 2 = 24 km/h. , 6. (x + 0, 5) + 42 = 24. x t 1 = (x + 0, 5) h, t 2= x h, x = 2, 5 hod. s 1 = 6. (x + 0, 5) s 2 = 24. x s = 24. 2, 5 = 60 km Cyklista dohoní chodca o 2, 5 hodiny, 60 km od B.

Slovné úlohy o spoločnej práci Pri riešení úloh o spoločnej práci vyjadríme: 1. Akú časť práce vykoná jeden zúčastnený za 1 časovú jednotku (deň, hodina, minúta. . . ) x časových jednotiek 2. Akú časť práce vykonajú všetci zúčastnení za x časových jednotiek Chodec prešiel dráhu za 6 hodín. Akú časť dráhy prešiel za: a) 1 hodinu, a) za 1 hodinu. . . b) 5 hodín, c) x hodín , b) za 5 hodín. . , c) za x hodín. . .

Majster by splnil úlohu za 20 hodín, učeň za 30 hodín. Za koľko hodín splnia úlohu, keď budú pracovať spoločne? Majster za 20 hodín, za 1 hodinu. . . za x hodín. . . učeň za 30 hodín, za 1 hodinu. . . za x hodín. . Za x hodín splnia celú prácu. Zostavenie rovnice a jej riešenie: Skúška: Majster. . . Učeň. . . Spolu. . Spolu urobia prácu za 12 hodín

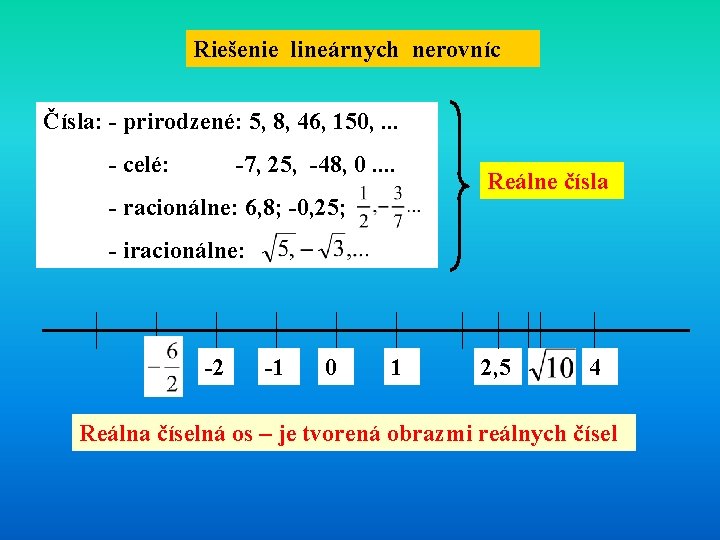
Riešenie lineárnych nerovníc Čísla: - prirodzené: 5, 8, 46, 150, . . . - celé: -7, 25, -48, 0. . - racionálne: 6, 8; -0, 25; Reálne čísla - iracionálne: -2 -1 0 1 2, 5 4 Reálna číselná os – je tvorená obrazmi reálnych čísel

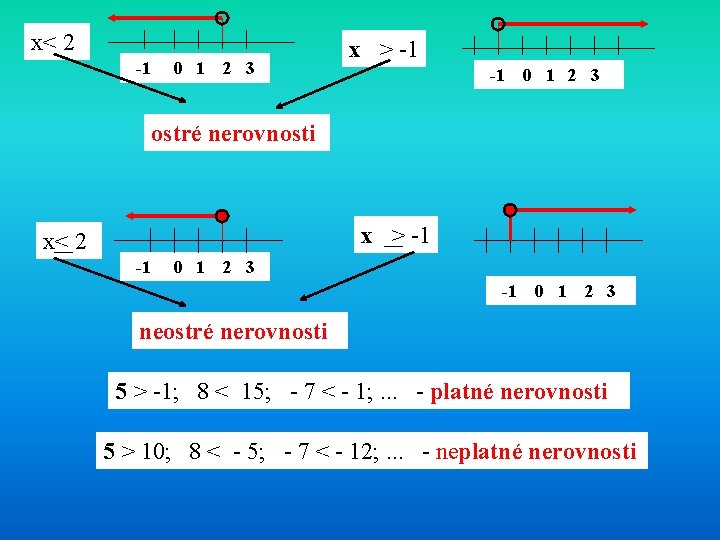
x< 2 -1 0 1 2 3 x > -1 -1 0 1 2 3 ostré nerovnosti x > -1 x< 2 -1 0 1 2 3 neostré nerovnosti 5 > -1; 8 < 15; - 7 < - 1; . . . - platné nerovnosti 5 > 10; 8 < - 5; - 7 < - 12; . . . - neplatné nerovnosti

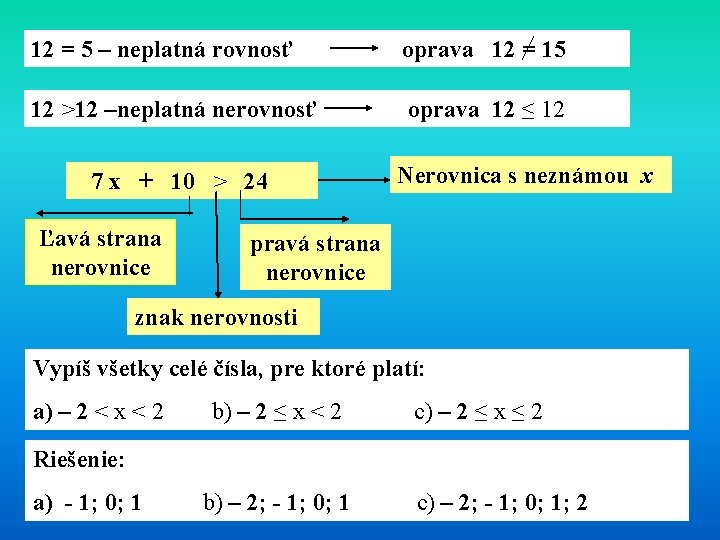
12 = 5 – neplatná rovnosť oprava 12 = 15 12 >12 –neplatná nerovnosť oprava 12 ≤ 12 7 x + 10 > 24 Ľavá strana nerovnice Nerovnica s neznámou x pravá strana nerovnice znak nerovnosti Vypíš všetky celé čísla, pre ktoré platí: a) – 2 < x < 2 b) – 2 ≤ x < 2 c) – 2 ≤ x ≤ 2 Riešenie: a) - 1; 0; 1 b) – 2; - 1; 0; 1 c) – 2; - 1; 0; 1; 2

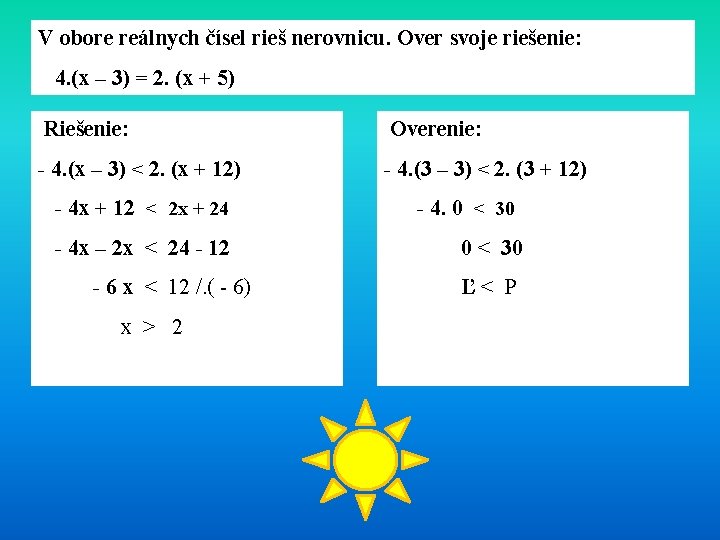
V obore reálnych čísel rieš nerovnicu. Over svoje riešenie: 4. (x – 3) = 2. (x + 5) Riešenie: Overenie: - 4. (x – 3) < 2. (x + 12) - 4. (3 – 3) < 2. (3 + 12) - 4 x + 12 < 2 x + 24 - 4 x – 2 x < 24 - 12 - 6 x < 12 /. ( - 6) x > 2 - 4. 0 < 30 Ľ< P

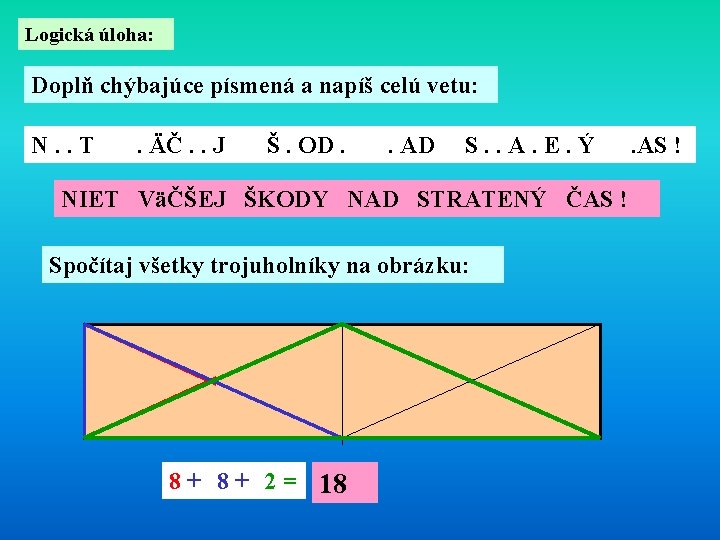
Logická úloha: Doplň chýbajúce písmená a napíš celú vetu: N. . T . ÄČ. . J Š. OD. . AD S. . A. E. Ý NIET VäČŠEJ ŠKODY NAD STRATENÝ ČAS ! Spočítaj všetky trojuholníky na obrázku: 8 + 2 = 18 . AS !