Grafick rieenie sstavy linernych rovnc a nerovnc s

Grafické riešenie sústavy lineárnych rovníc a nerovníc s dvomi neznámymi ¬ Grafické riešenie lineárnej rovnice ¬ Grafické riešenie sústavy lineárnych rovníc ¬ Grafické riešenie lineárnej nerovnice 1 Koniec

Grafom lineárnej rovnice ax 1+bx 2 =c , kde a, b, c sú reálne čísla, a≠ 0 alebo b≠ 0, je vždy priamka. 2 Začiatok Späť Ďalej Koniec

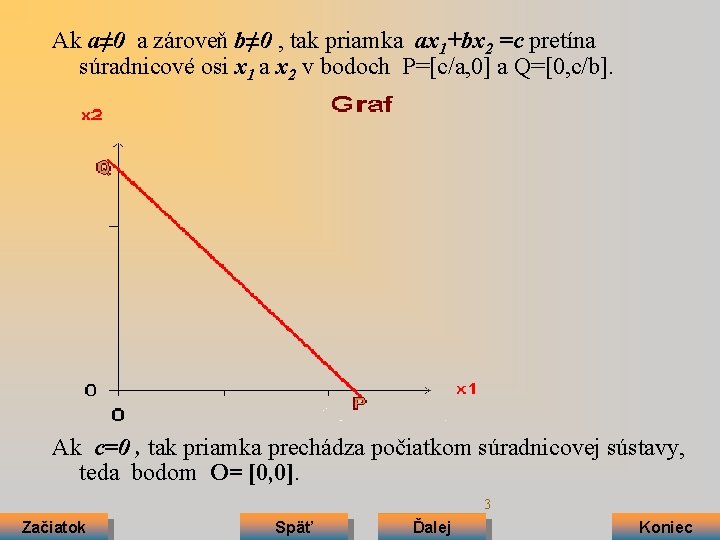
Ak a≠ 0 a zároveň b≠ 0 , tak priamka ax 1+bx 2 =c pretína súradnicové osi x 1 a x 2 v bodoch P=[c/a, 0] a Q=[0, c/b]. Ak c=0 , tak priamka prechádza počiatkom súradnicovej sústavy, teda bodom O= [0, 0]. 3 Začiatok Späť Ďalej Koniec

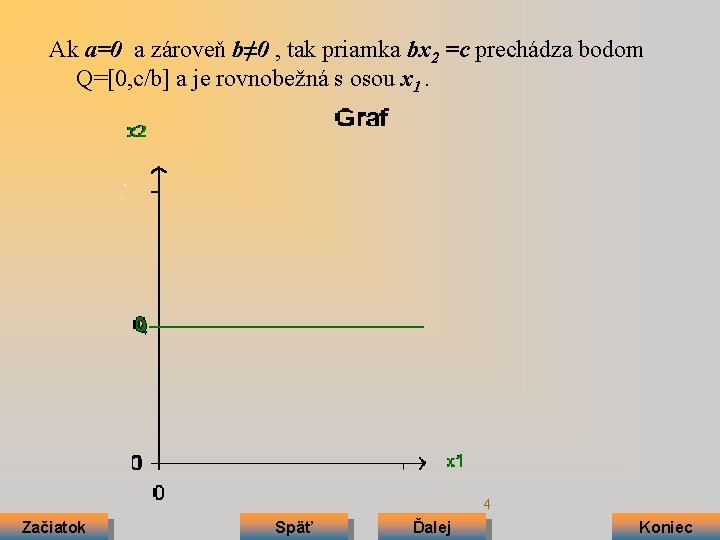
Ak a=0 a zároveň b≠ 0 , tak priamka bx 2 =c prechádza bodom Q=[0, c/b] a je rovnobežná s osou x 1. 4 Začiatok Späť Ďalej Koniec

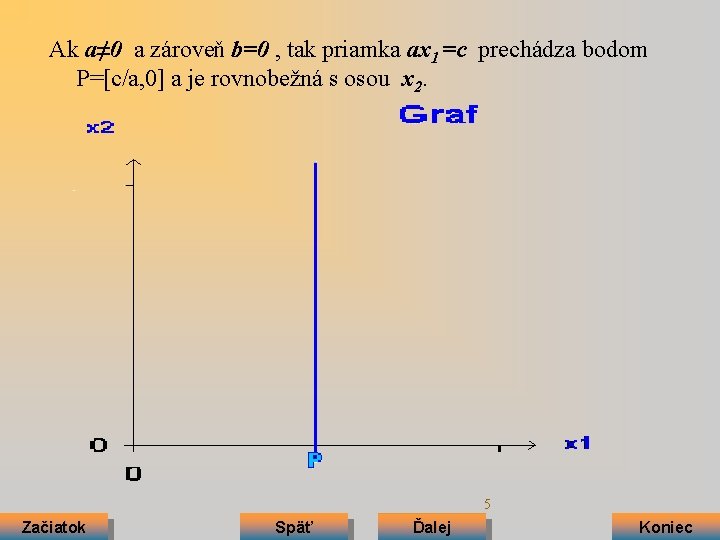
Ak a≠ 0 a zároveň b=0 , tak priamka ax 1 =c prechádza bodom P=[c/a, 0] a je rovnobežná s osou x 2. 5 Začiatok Späť Ďalej Koniec

Pokúste sa načrtnúť grafy lineárnych rovníc : ¬ 0, 04 x 2 = 2 ¬ 0, 05 x 1 =6 ¬ 0, 2 x 1 + 0, 1 x 2= 27 ¬ 35 x 1 + 42 x 2 = 0 RIEŠENIE 6 Začiatok Späť Ďalej Koniec

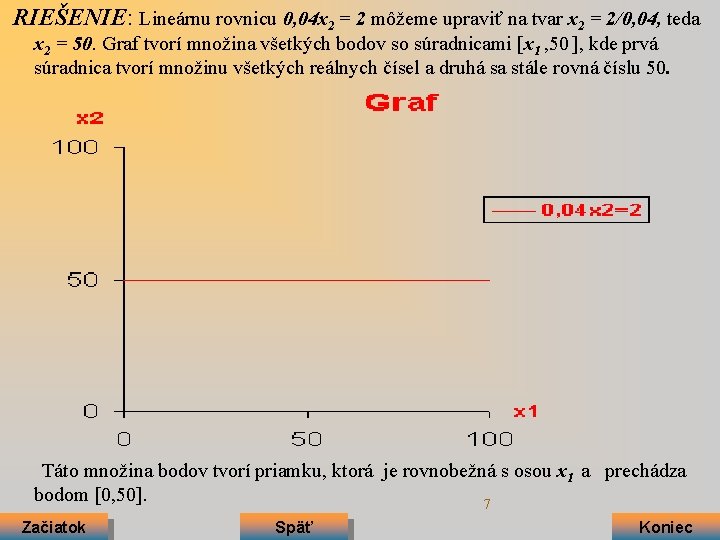
RIEŠENIE: Lineárnu rovnicu 0, 04 x 2 = 2 môžeme upraviť na tvar x 2 = 2/0, 04, teda x 2 = 50. Graf tvorí množina všetkých bodov so súradnicami [x 1 , 50 ], kde prvá súradnica tvorí množinu všetkých reálnych čísel a druhá sa stále rovná číslu 50. Táto množina bodov tvorí priamku, ktorá je rovnobežná s osou x 1 a prechádza bodom [0, 50]. 7 Začiatok Späť Koniec

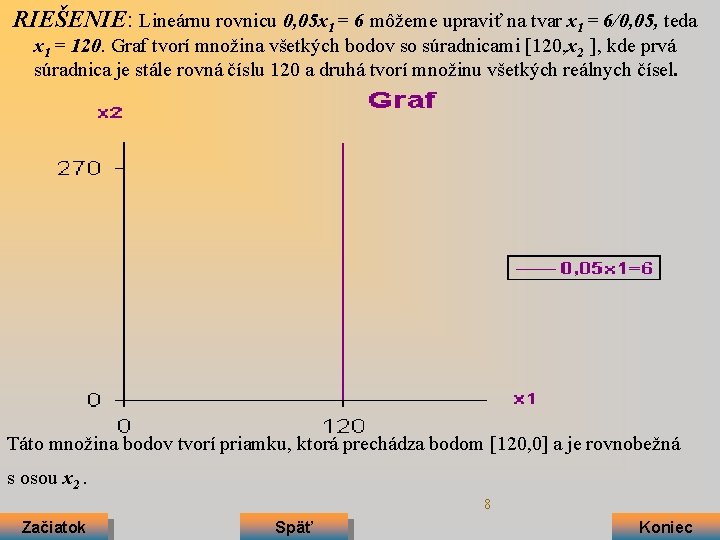
RIEŠENIE: Lineárnu rovnicu 0, 05 x 1 = 6 môžeme upraviť na tvar x 1 = 6/0, 05, teda x 1 = 120. Graf tvorí množina všetkých bodov so súradnicami [120, x 2 ], kde prvá súradnica je stále rovná číslu 120 a druhá tvorí množinu všetkých reálnych čísel. Táto množina bodov tvorí priamku, ktorá prechádza bodom [120, 0] a je rovnobežná s osou x 2. 8 Začiatok Späť Koniec

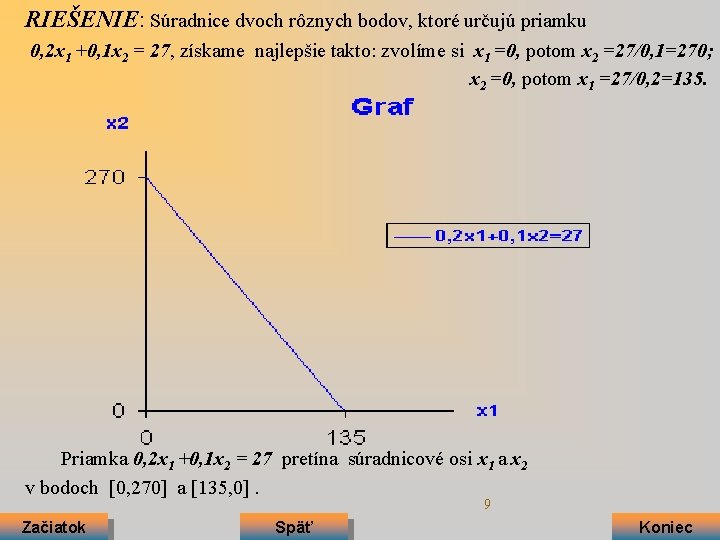
RIEŠENIE: Súradnice dvoch rôznych bodov, ktoré určujú priamku 0, 2 x 1 +0, 1 x 2 = 27, získame najlepšie takto: zvolíme si x 1 =0, potom x 2 =27/0, 1=270; x 2 =0, potom x 1 =27/0, 2=135. Priamka 0, 2 x 1 +0, 1 x 2 = 27 pretína súradnicové osi x 1 a x 2 v bodoch [0, 270] a [135, 0]. 9 Začiatok Späť Koniec

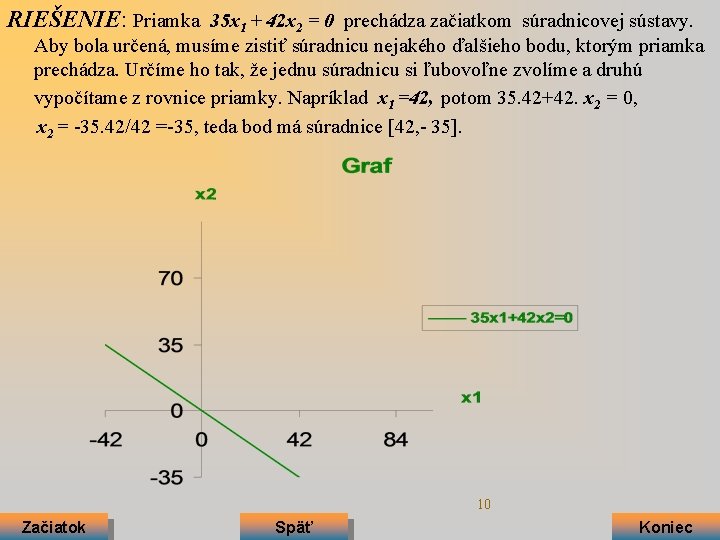
RIEŠENIE: Priamka 35 x 1 + 42 x 2 = 0 prechádza začiatkom súradnicovej sústavy. Aby bola určená, musíme zistiť súradnicu nejakého ďalšieho bodu, ktorým priamka prechádza. Určíme ho tak, že jednu súradnicu si ľubovoľne zvolíme a druhú vypočítame z rovnice priamky. Napríklad x 1 =42, potom 35. 42+42. x 2 = 0, x 2 = -35. 42/42 =-35, teda bod má súradnice [42, - 35]. 10 Začiatok Späť Koniec

Sústavu dvoch lineárnych rovníc s dvomi neznámymi riešime graficky tak, že do tej istej súradnicovej sústavy s osami x 1 a x 2 zakreslíme grafy oboch lineárnych rovníc. Body patriace do prieniku oboch grafov znázorňujú riešenie. Každý bod prieniku prvou súradnicou určuje koreň riešenia x 1 a druhou súradnicou koreň x 2. Prienikom príslušných priamok môže byť: ¬ prázdna množina, vtedy sústava rovníc nemá žiadne riešenie ( priamky sú rovnobežné ) PRÍKLAD ¬ jeden bod, sústava lineárnych rovníc má jediné riešenie ( priamky sú rôznobežné ) PRÍKLAD ¬ Nekonečne veľa bodov, keď sústava rovníc má nekonečne veľa riešení ( priamky sú totožné) PRÍKLAD 11 Začiatok Späť Ďalej Koniec

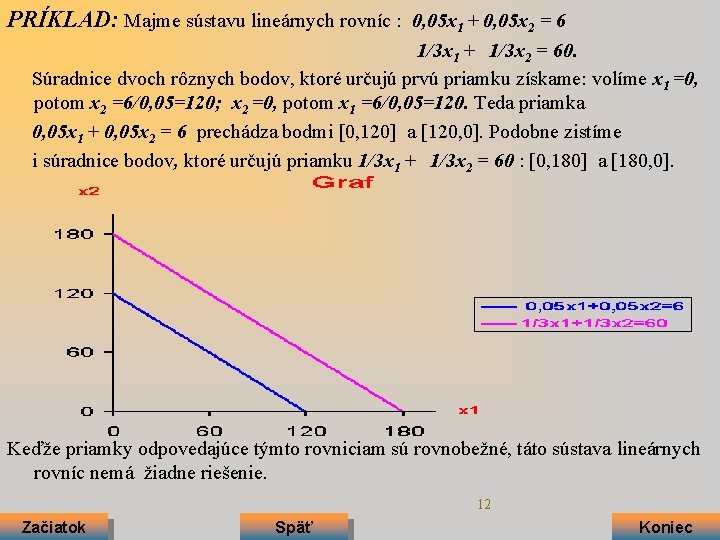
PRÍKLAD: Majme sústavu lineárnych rovníc : 0, 05 x 1 + 0, 05 x 2 = 6 1/3 x 1 + 1/3 x 2 = 60. Súradnice dvoch rôznych bodov, ktoré určujú prvú priamku získame: volíme x 1 =0, potom x 2 =6/0, 05=120; x 2 =0, potom x 1 =6/0, 05=120. Teda priamka 0, 05 x 1 + 0, 05 x 2 = 6 prechádza bodmi [0, 120] a [120, 0]. Podobne zistíme i súradnice bodov, ktoré určujú priamku 1/3 x 1 + 1/3 x 2 = 60 : [0, 180] a [180, 0]. Keďže priamky odpovedajúce týmto rovniciam sú rovnobežné, táto sústava lineárnych rovníc nemá žiadne riešenie. 12 Začiatok Späť Koniec

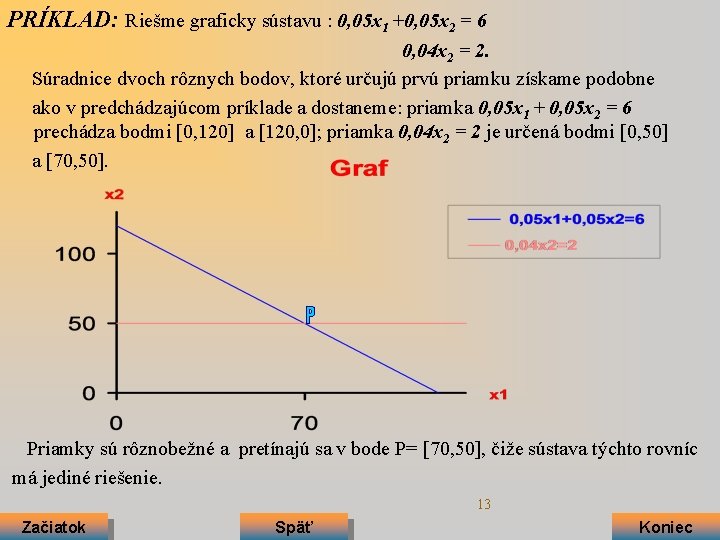
PRÍKLAD: Riešme graficky sústavu : 0, 05 x 1 +0, 05 x 2 = 6 0, 04 x 2 = 2. Súradnice dvoch rôznych bodov, ktoré určujú prvú priamku získame podobne ako v predchádzajúcom príklade a dostaneme: priamka 0, 05 x 1 + 0, 05 x 2 = 6 prechádza bodmi [0, 120] a [120, 0]; priamka 0, 04 x 2 = 2 je určená bodmi [0, 50] a [70, 50]. Priamky sú rôznobežné a pretínajú sa v bode P= [70, 50], čiže sústava týchto rovníc má jediné riešenie. 13 Začiatok Späť Koniec

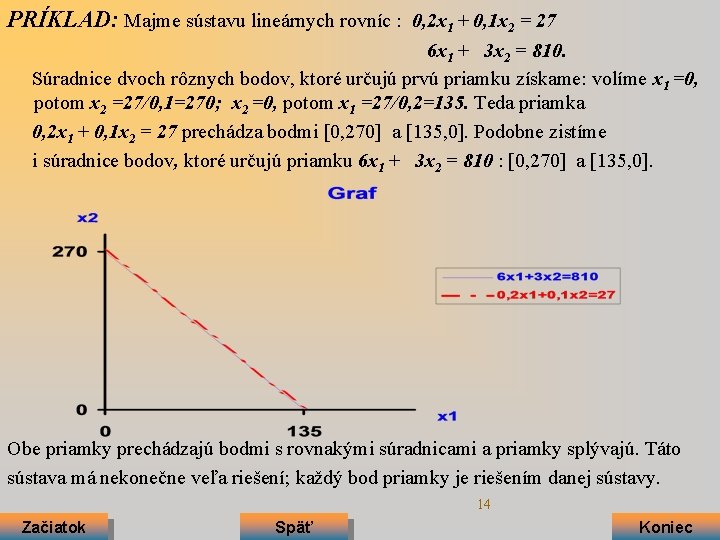
PRÍKLAD: Majme sústavu lineárnych rovníc : 0, 2 x 1 + 0, 1 x 2 = 27 6 x 1 + 3 x 2 = 810. Súradnice dvoch rôznych bodov, ktoré určujú prvú priamku získame: volíme x 1 =0, potom x 2 =27/0, 1=270; x 2 =0, potom x 1 =27/0, 2=135. Teda priamka 0, 2 x 1 + 0, 1 x 2 = 27 prechádza bodmi [0, 270] a [135, 0]. Podobne zistíme i súradnice bodov, ktoré určujú priamku 6 x 1 + 3 x 2 = 810 : [0, 270] a [135, 0]. Obe priamky prechádzajú bodmi s rovnakými súradnicami a priamky splývajú. Táto sústava má nekonečne veľa riešení; každý bod priamky je riešením danej sústavy. 14 Začiatok Späť Koniec

Pokúste sa načrtnúť grafické riešenie sústavy lineárnych rovníc : ¬ 0, 04 x 2 = 2 0, 2 x 1+0, 1 x 2= 27 RIEŠENIE 15 Začiatok Späť Koniec

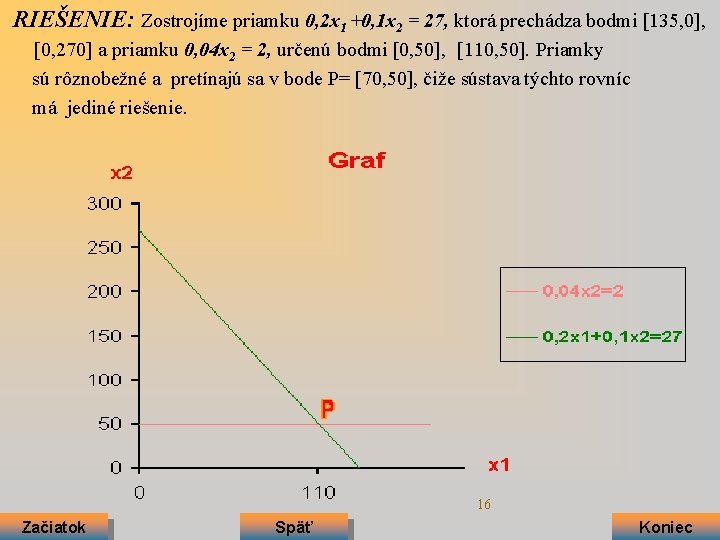
RIEŠENIE: Zostrojíme priamku 0, 2 x 1 +0, 1 x 2 = 27, ktorá prechádza bodmi [135, 0], [0, 270] a priamku 0, 04 x 2 = 2, určenú bodmi [0, 50], [110, 50]. Priamky sú rôznobežné a pretínajú sa v bode P= [70, 50], čiže sústava týchto rovníc má jediné riešenie. 16 Začiatok Späť Koniec

Priamka ax 1+bx 2 =c, kde a, b, c sú reálne čísla, a≠ 0 alebo b≠ 0, rozdeľuje rovinu na dve opačné polroviny a nazýva sa hraničnou priamkou. Grafickým riešením lineárnej nerovnice s dvomi neznámymi ax 1+bx 2 < c , kde a, b, c sú reálne čísla, a≠ 0 alebo b≠ 0, je vždy polrovina, teda množina bodov [x 1 , x 2 ], ktorých súradnice vyhovujú nerovnici ax 1+bx 2 < c. V nerovnici namiesto znaku <, môžu byť znaky: <=, >. Ak je v nerovnici použitý jeden zo znakov <=, >=, potom tejto nerovnici vyhovujú aj body patriace hraničnej priamke. 17 Začiatok Späť Ďalej Koniec

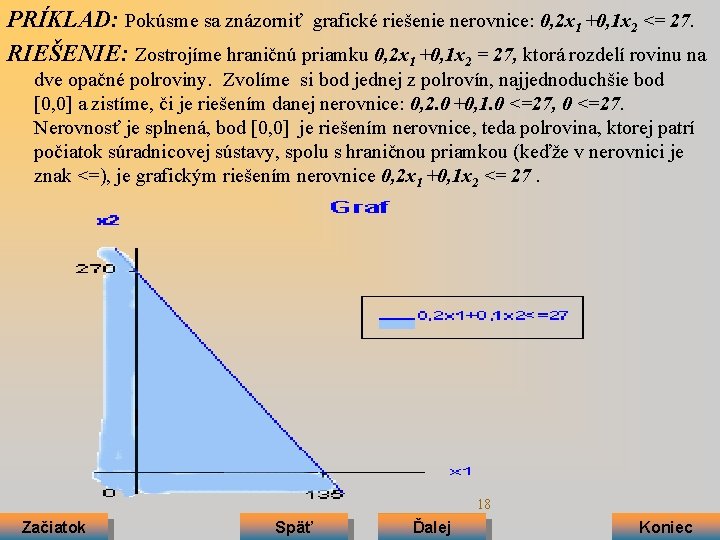
PRÍKLAD: Pokúsme sa znázorniť grafické riešenie nerovnice: 0, 2 x 1 +0, 1 x 2 <= 27. RIEŠENIE: Zostrojíme hraničnú priamku 0, 2 x 1 +0, 1 x 2 = 27, ktorá rozdelí rovinu na dve opačné polroviny. Zvolíme si bod jednej z polrovín, najjednoduchšie bod [0, 0] a zistíme, či je riešením danej nerovnice: 0, 2. 0 +0, 1. 0 <=27, 0 <=27. Nerovnosť je splnená, bod [0, 0] je riešením nerovnice, teda polrovina, ktorej patrí počiatok súradnicovej sústavy, spolu s hraničnou priamkou (keďže v nerovnici je znak <=), je grafickým riešením nerovnice 0, 2 x 1 +0, 1 x 2 <= 27. 18 Začiatok Späť Ďalej Koniec

Pokúste sa načrtnúť grafické riešenie lineárnych nerovníc : ¬ 0, 04 x 2 <= 2 ¬ 0, 05 x 1 >6 ¬ 35 x 1 + 42 x 2 > = 0 RIEŠENIE 19 Začiatok Späť Koniec

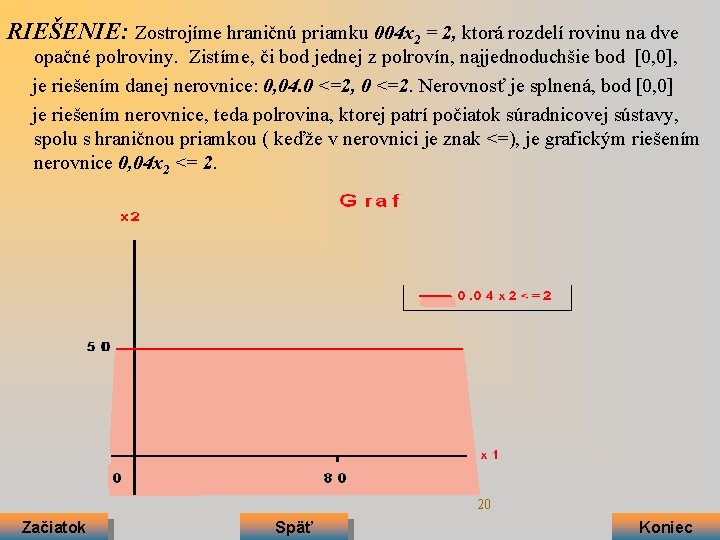
RIEŠENIE: Zostrojíme hraničnú priamku 004 x 2 = 2, ktorá rozdelí rovinu na dve opačné polroviny. Zistíme, či bod jednej z polrovín, najjednoduchšie bod [0, 0], je riešením danej nerovnice: 0, 04. 0 <=2, 0 <=2. Nerovnosť je splnená, bod [0, 0] je riešením nerovnice, teda polrovina, ktorej patrí počiatok súradnicovej sústavy, spolu s hraničnou priamkou ( keďže v nerovnici je znak <=), je grafickým riešením nerovnice 0, 04 x 2 <= 2. 20 Začiatok Späť Koniec

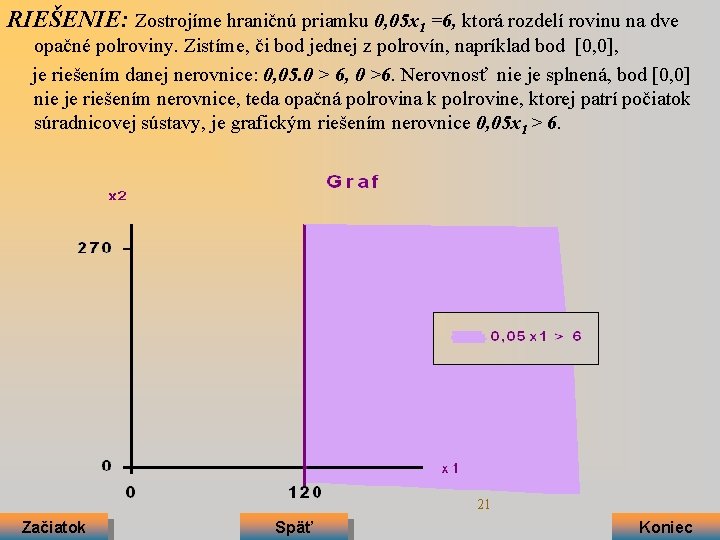
RIEŠENIE: Zostrojíme hraničnú priamku 0, 05 x 1 =6, ktorá rozdelí rovinu na dve opačné polroviny. Zistíme, či bod jednej z polrovín, napríklad bod [0, 0], je riešením danej nerovnice: 0, 05. 0 > 6, 0 >6. Nerovnosť nie je splnená, bod [0, 0] nie je riešením nerovnice, teda opačná polrovina k polrovine, ktorej patrí počiatok súradnicovej sústavy, je grafickým riešením nerovnice 0, 05 x 1 > 6. 21 Začiatok Späť Koniec

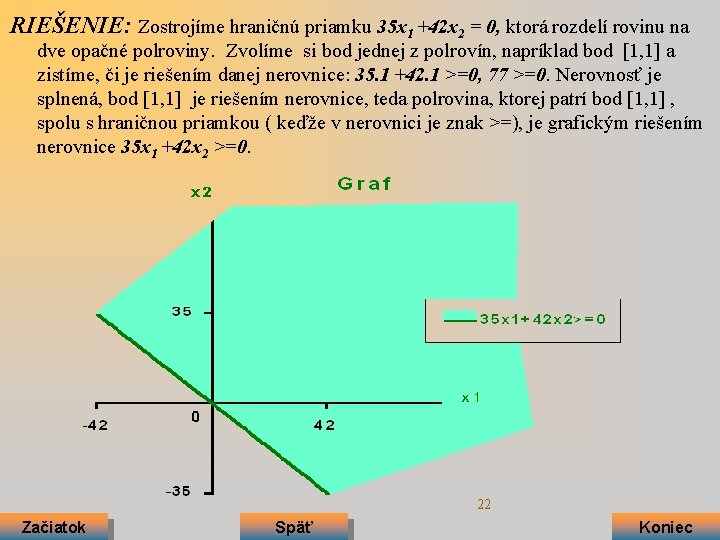
RIEŠENIE: Zostrojíme hraničnú priamku 35 x 1 +42 x 2 = 0, ktorá rozdelí rovinu na dve opačné polroviny. Zvolíme si bod jednej z polrovín, napríklad bod [1, 1] a zistíme, či je riešením danej nerovnice: 35. 1 +42. 1 >=0, 77 >=0. Nerovnosť je splnená, bod [1, 1] je riešením nerovnice, teda polrovina, ktorej patrí bod [1, 1] , spolu s hraničnou priamkou ( keďže v nerovnici je znak >=), je grafickým riešením nerovnice 35 x 1 +42 x 2 >=0. 22 Začiatok Späť Koniec