Luas Bangun Datar k i a l a

Luas Bangun Datar k i a l a ’ u m a l ssa Oleh : A W um Endah Fitri Suryanti A. 410 090 254 . b r. W

SK KD i s r ntedna i a u j ptaeenrjiar ns Tum aaerte t l S e a o Kem. Mb. Dm asp P Koan TUJUA N MATERI Menghitung keliling dan luas bangun • Menentukan Peserta didikserta dapat Luas segiempat • menentukan Memahami konsep Luas Bangun Datar menggunakannya segiempat dan segitiga Bangun Datar (segi dalam pemecahan serta menentukan empat dan segitiga) ukurannya. masalah By : Endah Fitri Suryanti

Luas Bangun Datar Persegi panjang Persegi Layang-layang Jajar genjang Segitiga Belah Ketupat Trapesium B a n g u n D a t a r

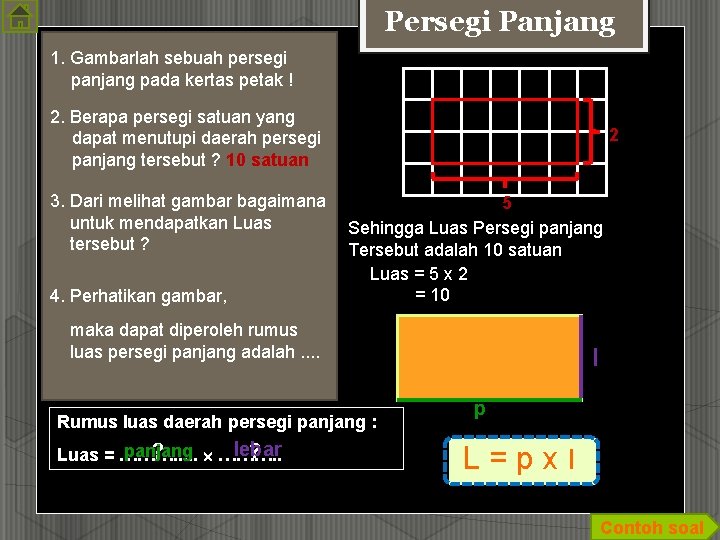
Persegi Panjang 1. Gambarlah sebuah persegi panjang pada kertas petak ! 2. Berapa persegi satuan yang dapat menutupi daerah persegi panjang tersebut ? 10 satuan 2 3. Dari melihat gambar bagaimana 5 untuk mendapatkan Luas Sehingga Luas Persegi panjang tersebut ? Tersebut adalah 10 satuan Luas = 5 x 2 = 10 4. Perhatikan gambar, maka dapat diperoleh rumus luas persegi panjang adalah. . Rumus luas daerah persegi panjang : lebar panjang ? ? Luas = ………. . l p L = p x l Contoh soal

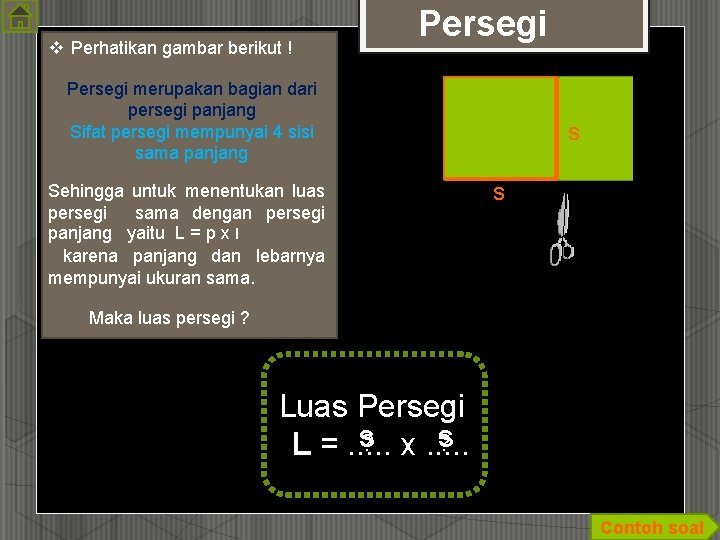
v Perhatikan gambar berikut ! Persegi merupakan bagian dari persegi panjang Sifat persegi mempunyai 4 sisi sama panjang Sehingga untuk menentukan luas persegi sama dengan persegi panjang yaitu L = p x l karena panjang dan lebarnya mempunyai ukuran sama. s s Maka luas persegi ? Luas Persegi s? s? L =. . . x. . . Contoh soal

Segitiga Persegi panjang dipotong pada salah satu diagonalnya sehingga menjadi 2 segitiga yang sama. Jika panjang persegi panjang sebagai alas segitiga t l maka tinggi segitiga =. . . Persegi panjang ┐ a Tinggi segitiga ┴ alasnya. Tinggi segitiga Contoh soal

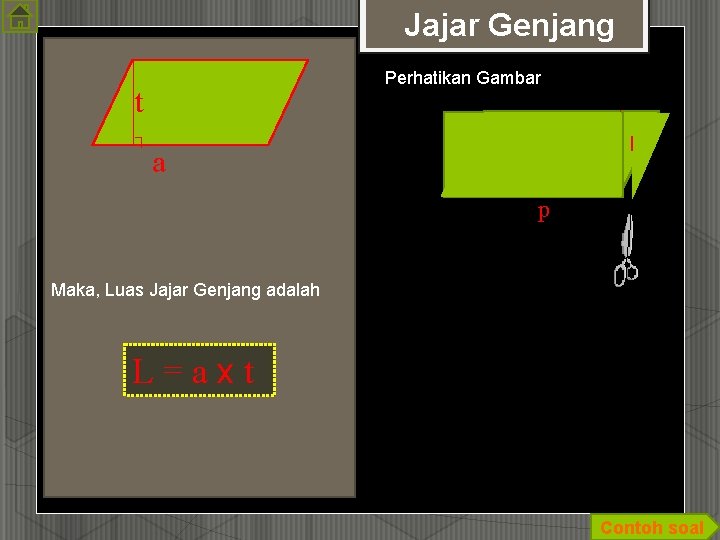
Jajar Genjang Perhatikan Gambar t ┐ l a ┌ p Maka, Luas Jajar Genjang adalah L=axt Contoh soal

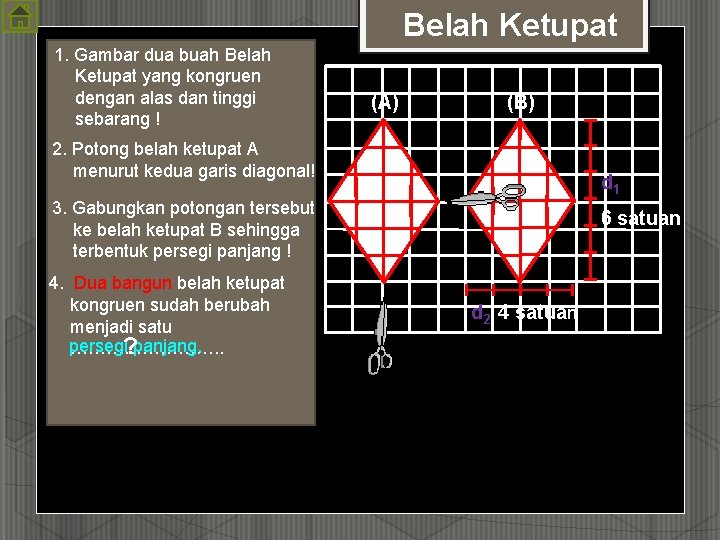
Belah Ketupat 1. Gambar dua buah Belah Ketupat yang kongruen dengan alas dan tinggi sebarang ! (A) (B) 2. Potong belah ketupat A menurut kedua garis diagonal! d 1 3. Gabungkan potongan tersebut ke belah ketupat B sehingga terbentuk persegi panjang ! 4. Dua bangun belah ketupat kongruen sudah berubah menjadi satu persegi panjang, ? …………. . 6 satuan d 2 4 satuan

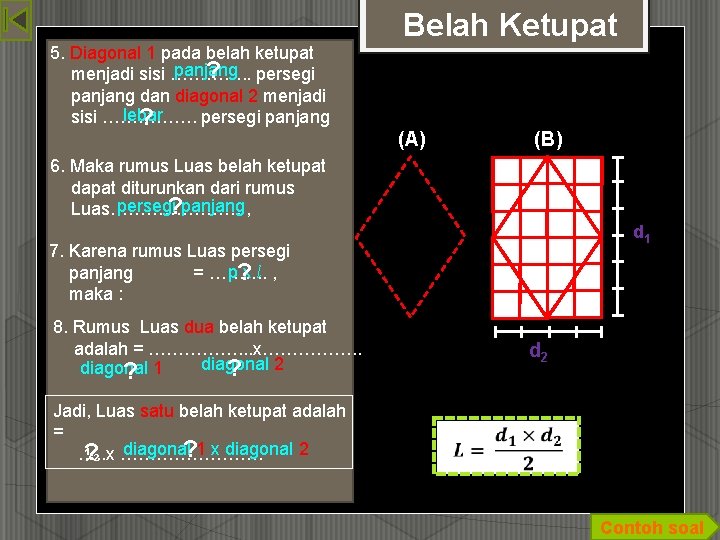
5. Diagonal 1 pada belah ketupat panjang ? menjadi sisi …………. . persegi panjang dan diagonal 2 menjadi lebar sisi ……………. persegi panjang ? Belah Ketupat (A) (B) 6. Maka rumus Luas belah ketupat dapat diturunkan dari rumus persegi panjang ? Luas…………………. , d 1 7. Karena rumus Luas persegi p x l panjang = ………. , ? maka : 8. Rumus Luas dua belah ketupat adalah = ……………. . . x……………. . diagonal 2 diagonal 1 ? ? Jadi, Luas satu belah ketupat adalah = ? ? …. . x ………… ½ diagonal 1 x diagonal 2 d 2 Contoh soal

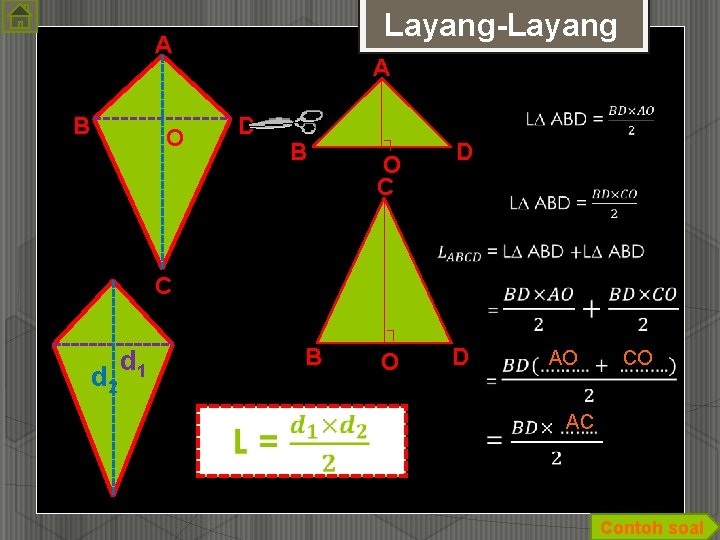
Layang-Layang A B A D O B ┐ D O C C ┐ d 2 B d 1 O D AO CO AC Contoh soal

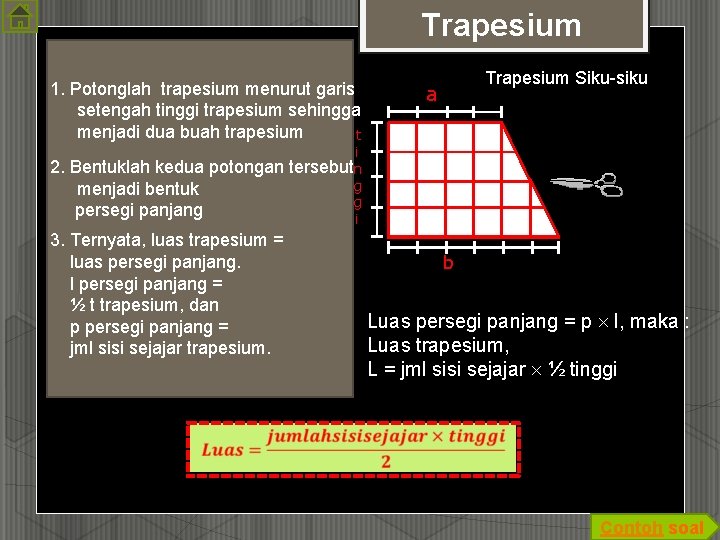
Trapesium 1. Potonglah trapesium menurut garis setengah tinggi trapesium sehingga menjadi dua buah trapesium t Trapesium Siku-siku a i 2. Bentuklah kedua potongan tersebut n g menjadi bentuk g persegi panjang i 3. Ternyata, luas trapesium = luas persegi panjang. l persegi panjang = ½ t trapesium, dan p persegi panjang = jml sisi sejajar trapesium. b Luas persegi panjang = p l, maka : Luas trapesium, L = jml sisi sejajar ½ tinggi Contoh soal

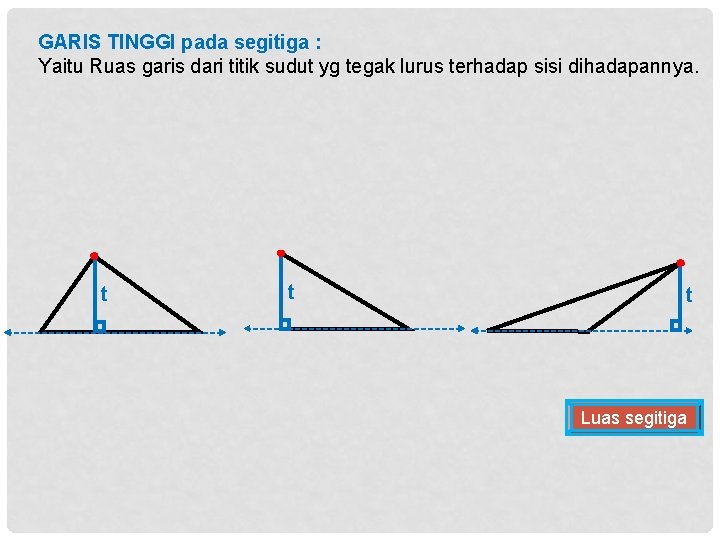
GARIS TINGGI pada segitiga : Yaitu Ruas garis dari titik sudut yg tegak lurus terhadap sisi dihadapannya. t t t Luas segitiga

Contoh Soal Rumus Sebuah persegi panjang mempunyai panjang 8 cm dan lebar 5 cm. Tentukan luas persegi panjang tersebut! Penyelesaian : Diketahui : p =8 cm dan lebar 5 cm Ditanya : Luas persegi panjang? Jawab : L = p x l L = 8 x 5 = 40 cm 2

Contoh Soal Rumus Sebuah persegi mempunyai keliling 24 cm. Tentukan luas persegi tersebut! Penyelesaian : Diketahui : keliling persegi = 24 cm Ditanya : Luas persegi ? Jawab : Ingat : Persegi mempunyai 4 sisi yang sama panjang L = s x s L = 6 x 6 = 36 cm 2

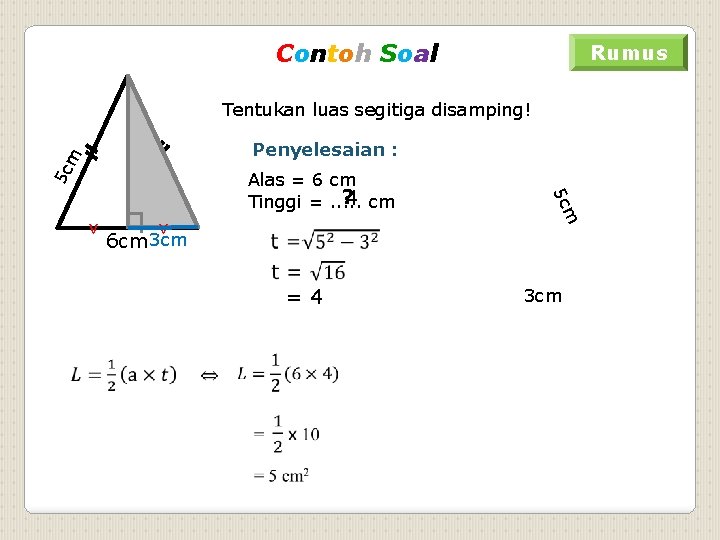
Contoh Soal Rumus Tentukan luas segitiga disamping! Penyelesaian : 5 c m t ┐v 6 cm 3 cm m 5 c v Alas = 6 cm ? 4 Tinggi =. . . cm = 4 3 cm

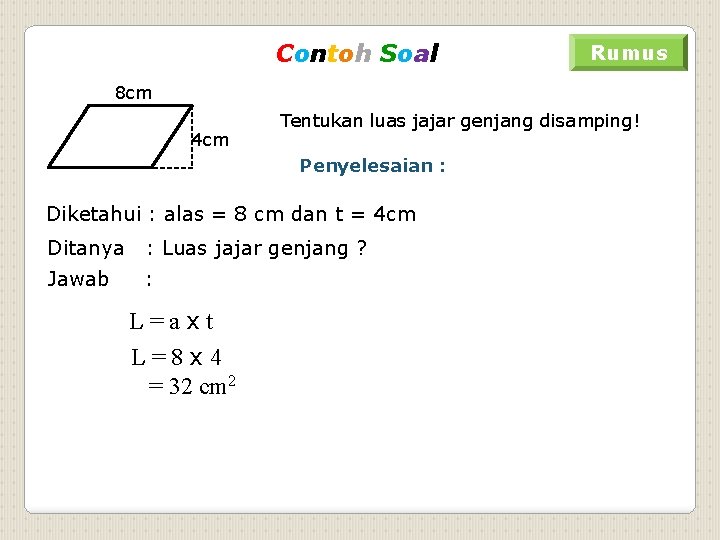
Contoh Soal Rumus 8 cm 4 cm Tentukan luas jajar genjang disamping! Penyelesaian : Diketahui : alas = 8 cm dan t = 4 cm Ditanya : Luas jajar genjang ? Jawab : L=axt L=8 x 4 = 32 cm 2

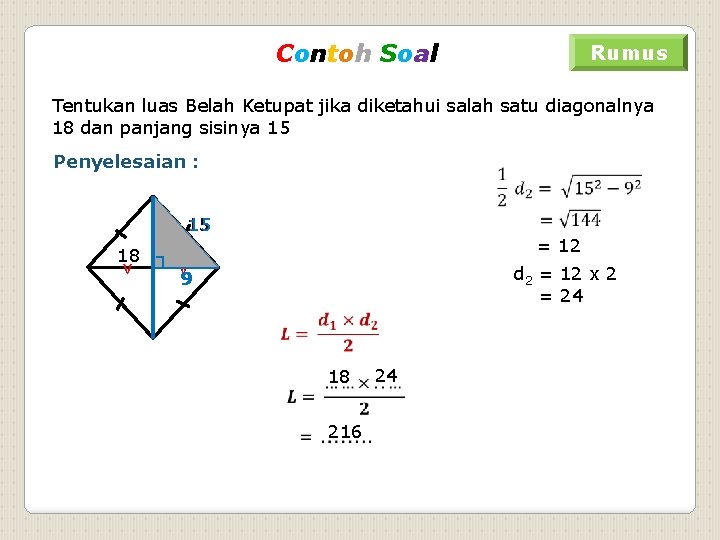
Contoh Soal Rumus Tentukan luas Belah Ketupat jika diketahui salah satu diagonalnya 18 dan panjang sisinya 15 Penyelesaian : 15 = 12 18 ┐ v v 9 9 d 2 = 12 x 2 = 24 18 216 24

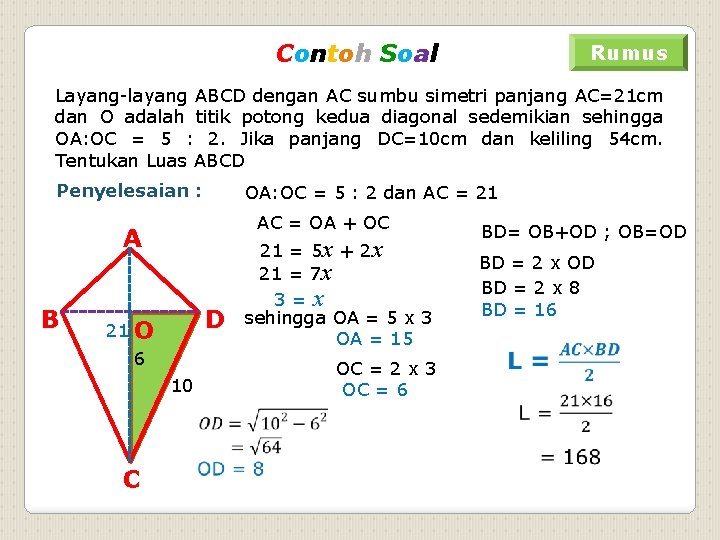
Contoh Soal Rumus Layang-layang ABCD dengan AC sumbu simetri panjang AC=21 cm dan O adalah titik potong kedua diagonal sedemikian sehingga OA: OC = 5 : 2. Jika panjang DC=10 cm dan keliling 54 cm. Tentukan Luas ABCD Penyelesaian : OA: OC = 5 : 2 dan AC = 21 AC = OA + OC A B D 21 O 6 10 C 21 = 5 x + 2 x 21 = 7 x 3 = x sehingga OA = 5 x 3 OA = 15 OC = 2 x 3 OC = 6 BD= OB+OD ; OB=OD BD = 2 x 8 BD = 16

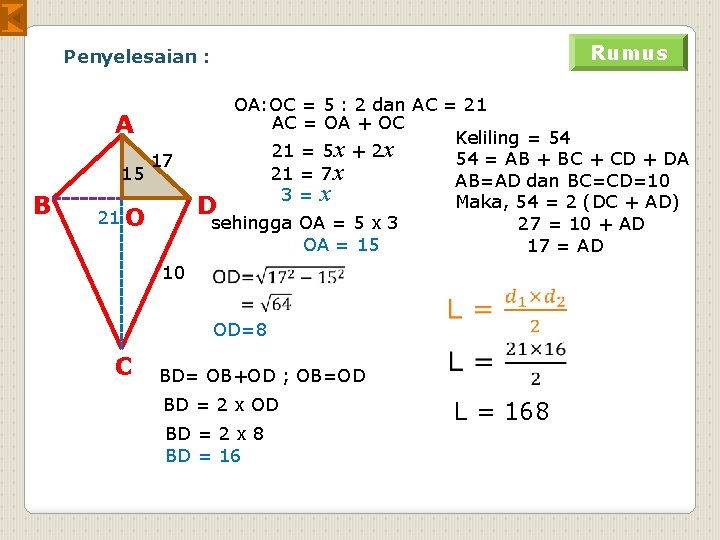
Rumus Penyelesaian : A 15 B 17 21 O 10 OA: OC = 5 : 2 dan AC = 21 AC = OA + OC Keliling = 54 21 = 5 x + 2 x 54 = AB + BC + CD + DA 21 = 7 x AB=AD dan BC=CD=10 3 = x Maka, 54 = 2 (DC + AD) D sehingga OA = 5 x 3 27 = 10 + AD OA = 15 17 = AD OD=8 C BD= OB+OD ; OB=OD BD = 2 x 8 BD = 16 L = 168

Contoh Soal Rumus Trapesium sama kaki mempunyai panjang kaki 20. sisi sejajar masing-masing 12 dan 36. tentukan tinggi dan luas trapesium tersebut! Penyelesaian : 12 t 36 36 -12=24 24: 2 =12 20 ┐ 12 t = 16 Luas = 384

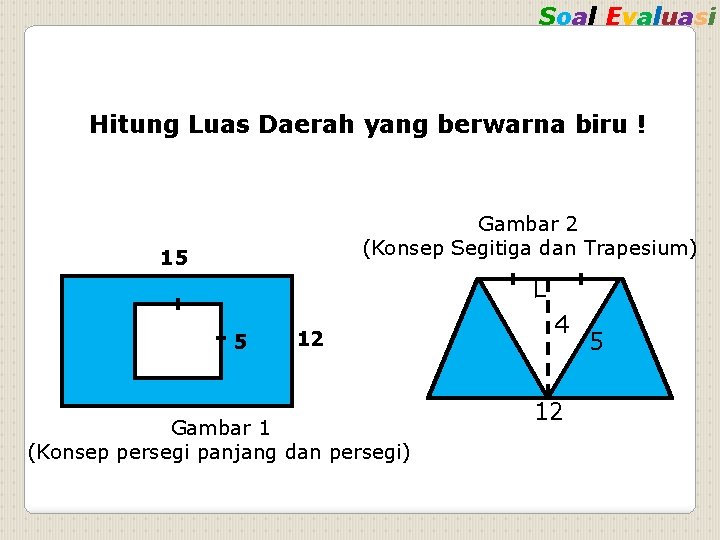
Soal Evaluasi Hitung Luas Daerah yang berwarna biru ! Gambar 2 (Konsep Segitiga dan Trapesium) 15 ┐ 5 12 Gambar 1 (Konsep persegi panjang dan persegi) 4 12 5

Soal Evaluasi Hitung Luas Daerah pada gambar di bawah ini ! 7 cm 13 5 cm 12 3 cm Gambar 4 (Jajargenjang) 15 Gambar 3 (Layang-layang) 20 16 Gambar 5 (Belah Ketupat)

Wassalamu’alaikum Wr. Wb. SEKIAN