KESEBANGUNAN Disusun Oleh Sohrah S Pd SMP Negeri

KESEBANGUNAN Disusun Oleh : Sohrah, S. Pd SMP Negeri 1 Batu Ampar

I. GAMBAR DAN MODEL BERSKALA Skala = Ukuran pada peta : Ukuran sebenarnya Sebutkan pengertian Skala! Ukuran pada peta atau Skala 1 : 3. 200. 000 Skala = Ukuran sebenarnya Contoh : 1 Dari Peta disamping diperoleh informasi bahwa ukuran pulau sebenarnya adalah 3. 200. 000 kali ukuran peta itu. Berapa km panjang pulau itu yang sebenarnya?

Penyelesaian : Diketahui Peta : Panjang = 4 cm dan Skala 1 : 3. 200. 000 Ditanya : Panjang Pulau sebenarnya = …. Jawab : Ukuran pada peta Skala = Ukuran sebenarnya 1 4 cm 3. 200. 000 = Ukuran sebenarnya 1 x Ukuran sebenarnya = 3. 200. 000 x 4 cm Ukuran sebenarnya = 12. 800. 000 cm = 128 km Jadi Panjang Pulau itu sebenarnya = 128 km

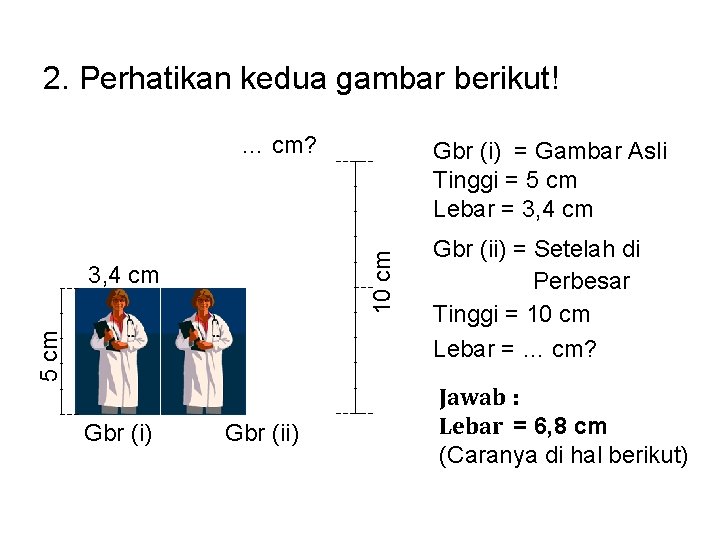
2. Perhatikan kedua gambar berikut! … cm? 10 cm 5 cm 3, 4 cm Gbr (i) = Gambar Asli Tinggi = 5 cm Lebar = 3, 4 cm Gbr (ii) = Setelah di Perbesar Tinggi = 10 cm Lebar = … cm? Jawab : Lebar = 6, 8 cm (Caranya di hal berikut)

Cara penyelesaiannya : Cara I : Menggunakan Perbandingan , sebagai berikut : Ukuran gambar Asli : Tinggi I = t 1 = 5 cm dan Lebar I = l 1 = 3, 4 cm Ukuran gambar setelah diperbesar : Tinggi II = t 2 = 10 cm dan Lebar II = l 2 = … cm Jawab : t 1 : t 2 = l 1 : l 2 5 : 10 = 3, 4 : l 2 Jadi Lebar setelah 5 x l 2 = 10 x 3, 4 diperbesar = 6, 8 cm 5 l 2 = 34 : 5 = 6, 8 Cara II : (10 cm : 5 cm ) x 3, 4 cm = 2 x 3, 4 cm = 6, 8 cm

3. Gambar disamping adalah Model Mobil Balap Model Mobil balap (Mobil mainan anak-anak) dengan Ukuran panjang = 6 cm , lebar = 2, 4 cm, tinggi = t cm Panjang mobil sebenarnya adalah 2, 76 m. Ditanya : a. Tentukan Skala model mobil itu. b. Tentukan lebar mobil sebenarnya. c. Jika tinggi mobil sebenarnya = 92 cm tentukanlah tinggi model. t

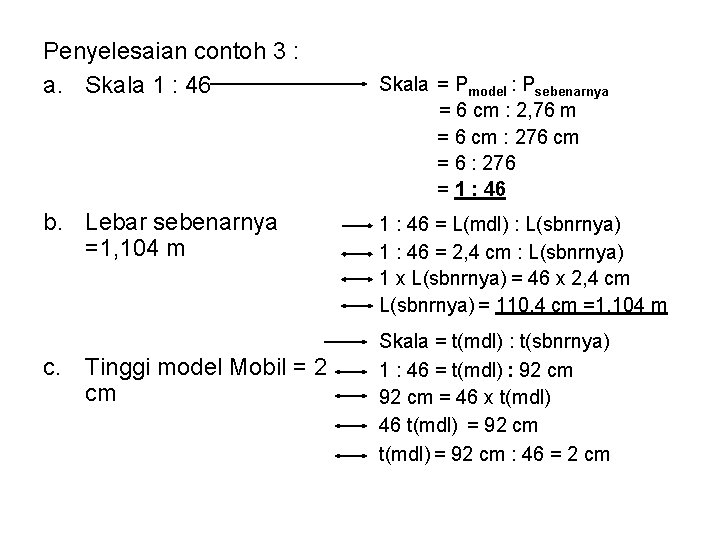
Penyelesaian contoh 3 : a. Skala 1 : 46 b. Lebar sebenarnya =1, 104 m c. Tinggi model Mobil = 2 cm Skala = Pmodel : Psebenarnya = 6 cm : 2, 76 m = 6 cm : 276 cm = 6 : 276 = 1 : 46 = L(mdl) : L(sbnrnya) 1 : 46 = 2, 4 cm : L(sbnrnya) 1 x L(sbnrnya) = 46 x 2, 4 cm L(sbnrnya) = 110, 4 cm =1, 104 m Skala = t(mdl) : t(sbnrnya) 1 : 46 = t(mdl) : 92 cm = 46 x t(mdl) 46 t(mdl) = 92 cm : 46 = 2 cm

KESIMPULAN Untuk menyelesaikan suatu soal yang berkaitan dengan perbandingan, dalam pembuatan perbandingannnya yang dipasangkan adalah yang sejenis. Misalnya : 1. Lebar pada gbr/peta/model dan Lebar sebenarnya 2. Panjang pada gbr/peta/model dan Panjang sebenarnya 3. Tinggi pada gbr/peta/model dan Tinggi

KESEBANGUNAN DAN KONGRUENSI BANGUN DATAR Standar Kompetensi : 1. Memahami kesebangunan bangun datar dan penggunaannya dalam pemecahan masalah. Kompetensi dasar : 1. 1. Mengidentifikasi bangun-bangun datar yang sebangun dan kongruen. 1. 2. Mengidentifikasi sifat-sifat dua segitiga sebangun dan kongruen. 1. 3. Menggunakan Konsep kesebangunan segitiga dalam pemecahan masalah.

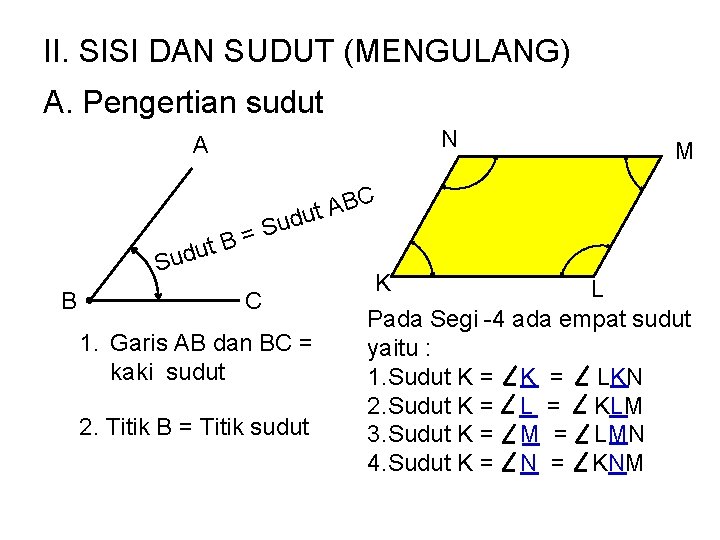
II. SISI DAN SUDUT (MENGULANG) A. Pengertian sudut N A Su = t. B C AB t u d u Sud B M C 1. Garis AB dan BC = kaki sudut 2. Titik B = Titik sudut K L Pada Segi -4 ada empat sudut yaitu : 1. Sudut K = LKN 2. Sudut K = L = KLM 3. Sudut K = M = LMN 4. Sudut K = N = KNM

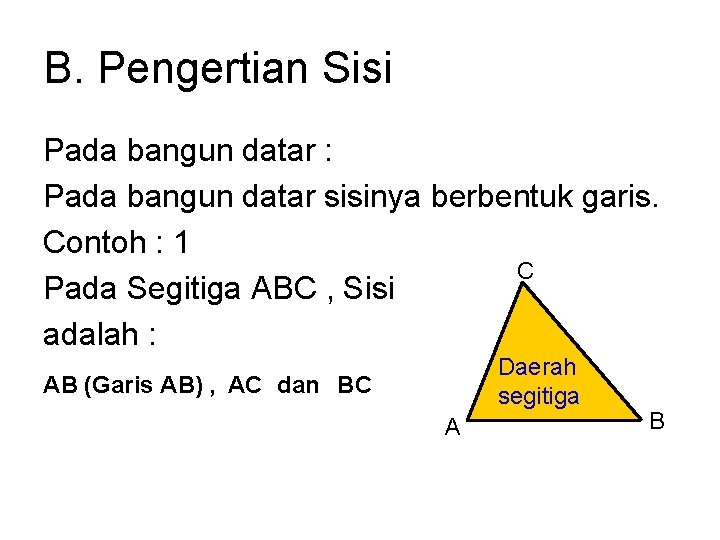
B. Pengertian Sisi Pada bangun datar : Pada bangun datar sisinya berbentuk garis. Contoh : 1 C Pada Segitiga ABC , Sisi adalah : Daerah segitiga AB (Garis AB) , AC dan BC A B

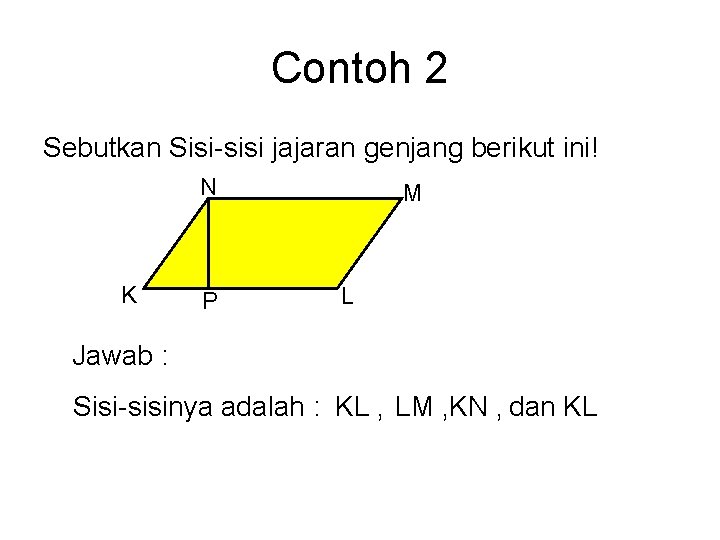
Contoh 2 Sebutkan Sisi-sisi jajaran genjang berikut ini! N K P M L Jawab : Sisi-sisinya adalah : KL , LM , KN , dan KL

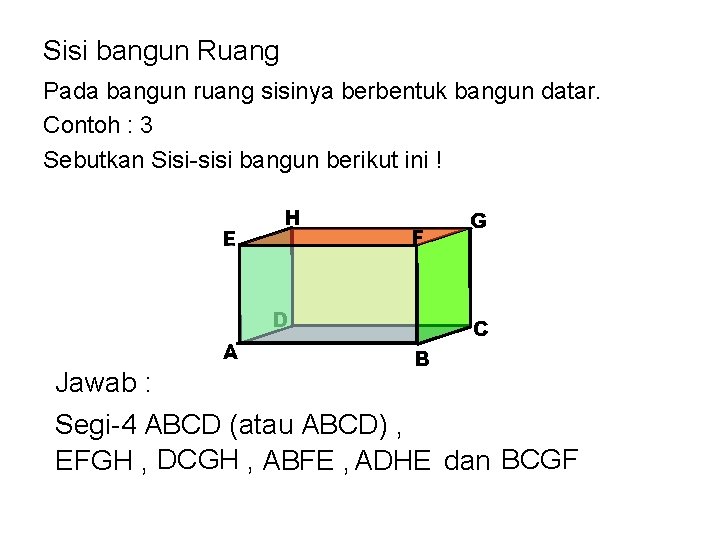
Sisi bangun Ruang Pada bangun ruang sisinya berbentuk bangun datar. Contoh : 3 Sebutkan Sisi-sisi bangun berikut ini ! E H F D A G C B Jawab : Segi-4 ABCD (atau ABCD) , EFGH , DCGH , ABFE , ADHE dan BCGF

III. KESEBANGUNAN

APA PENGERTIAN KESEBANGUNAN? Sebangun artinya Sama bentuk. Jadi Kesebangunan artinya Kesamaan bentuk. Dalam kesebangunan ini kita akan membahas masalah bentuk suatu benda (Bangun Datar) , misalnya tentang : 1). Dua Persegipanjang apakah bentuknya sama atau tidak. 2). Dua Trapesium apakah bentuknya sama atau tidak. 3). Jajaran genjang , dan lain-lain. Misalnya : Jika Adikmu saat ini menggambar sebuah Persegi di sekolahnya dan kamu juga menggambar sebuah persegi , maka persegi yang digambar adikmu pasti sebangun dengan yang kamu gambar.

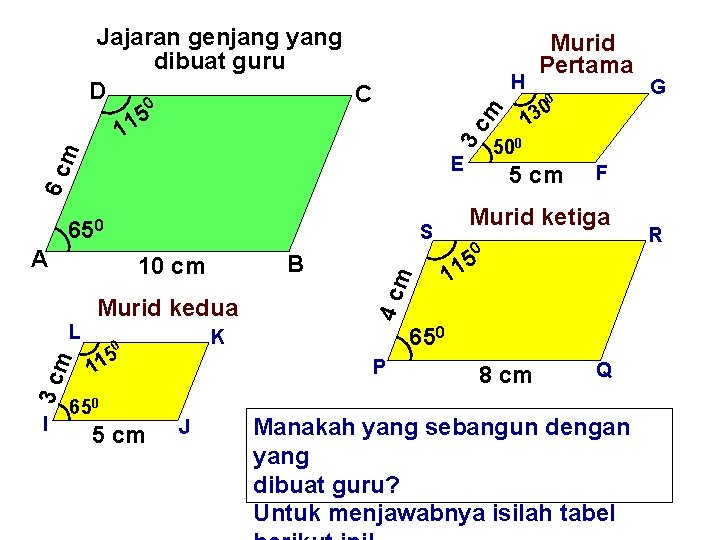
Jajaran genjang yang dibuat guru D C 0 5 1 1 H 3 c m I Murid kedua Murid ketiga 650 5 cm P J 0 5 11 650 K 0 5 11 m B G F 4 c L 5 cm S 10 cm 0 13 cm 3 m 6 c 650 0 500 E A Murid Pertama 8 cm Q Manakah yang sebangun dengan yang dibuat guru? Untuk menjawabnya isilah tabel R

Jajaran genjang Sisi Sudut Terpanja Terpende Terbesar Terkecil ng k Guru AB = 10 AD = 6 cm ∠D = 1150 ∠A = 650 cm IJ = 5 cm IL = 3 cm ∠L = 11500 ∠I = 6500 Murid (i) EF = 5 cm EH = 3 cm ∠H = 1300 ∠E = 500 PQ = 8 cm PS = 4 cm ∠S = 115 ∠P = 65 Murid (ii) …… …… 1). Buatan Guru dan Buatan Murid Pertama Murid …… …… a. Perbandingan Sisi Terpanjang adalah AB : EF = 10 : (iii) 5 = 2 : 1 Perbandingan Sisi Terpendek adalah AD : EH = 6 : 3 = 2 : 1 Kesimpulan : Perbandingan Sisi yang sesuai (perbandingan yang terpanjang dengan yang terpanjang dan perbandingan yang terpendek dengan yang terpendek) adalah sama , yaitu sama 2 : 1

• Guru menyatakan syarat kesebangunan dengan lisan. • Siswa membuat kesimpulan tentang hasil penelitian mengenai jajaran genjang buatan guru dan murid. Kesimpulan : ……………………………… ………. .

A. PENGERTIAN KESEBANGUNAN. 1). Sebangun artinya adalah Sama Bentuk 2). Kesebangunan berarti Kesamaan Bentuk. Syarat kesebangunan adalah : Dua benda (bangun datar) adalah sebangun (sama bentuk) jika pada kedua benda itu dijumpai syarat-syarat berikut : (i). Pasangan Sisi-sisi yang sesuai mempunyai perbandingan yang sama. (ii). Sudut-sudut yang sesuai sama besarnya.

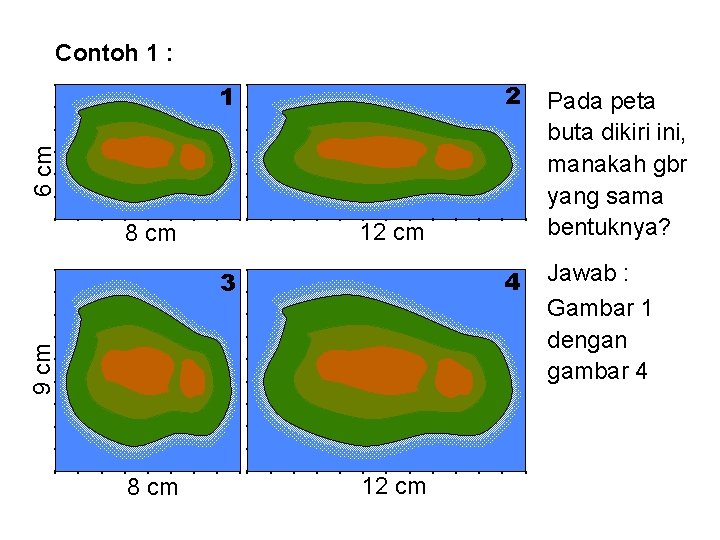
Contoh 1 : 2 Pada peta buta dikiri ini, manakah gbr yang sama bentuknya? 4 Jawab : Gambar 1 dengan gambar 4 6 cm 1 12 cm 8 cm 9 cm 3 8 cm 12 cm

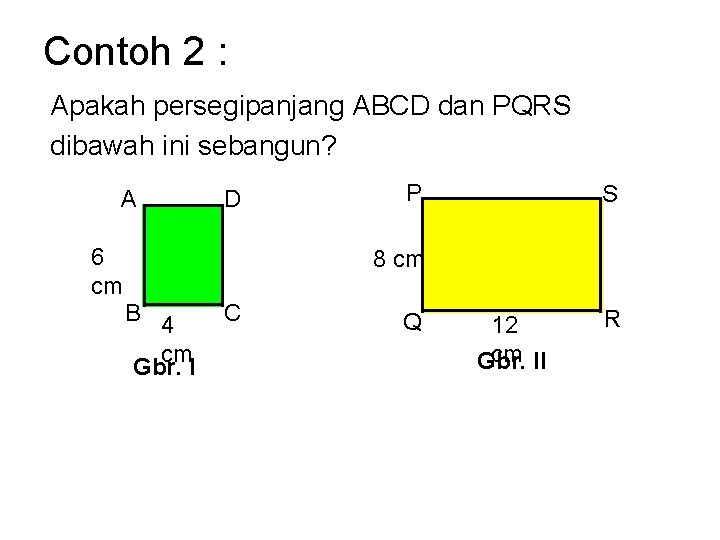
Contoh 2 : Apakah persegipanjang ABCD dan PQRS dibawah ini sebangun? A 6 cm D P S 8 cm B 4 cm Gbr. I C Q 12 cm II Gbr. R

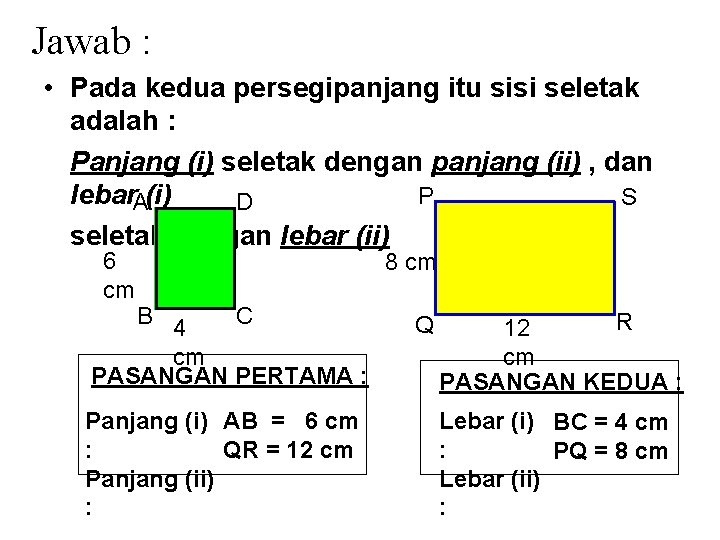
Jawab : • Pada kedua persegipanjang itu sisi seletak adalah : Panjang (i) seletak dengan panjang (ii) , dan P lebar. A(i) S D seletak dengan lebar (ii) 6 cm 8 cm B C 4 cm PASANGAN PERTAMA : Panjang (i) AB = 6 cm : QR = 12 cm Panjang (ii) : Q R 12 cm PASANGAN KEDUA : Lebar (i) BC = 4 cm : PQ = 8 cm Lebar (ii) :

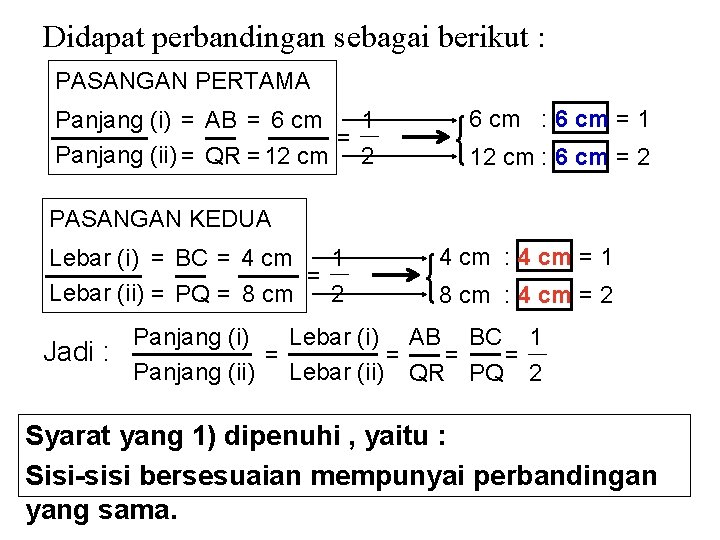
Didapat perbandingan sebagai berikut : PASANGAN PERTAMA Panjang (i) = AB = 6 cm 1 = Panjang (ii) = QR = 12 cm 2 6 cm : 6 cm = 1 12 cm : 6 cm = 2 PASANGAN KEDUA Lebar (i) = BC = 4 cm 1 = Lebar (ii) = PQ = 8 cm 2 4 cm : 4 cm = 1 8 cm : 4 cm = 2 Panjang (i) Lebar (i) AB BC 1 Jadi : = = Panjang (ii) Lebar (ii) QR PQ 2 Syarat yang 1) dipenuhi , yaitu : Sisi-sisi bersesuaian mempunyai perbandingan yang sama.

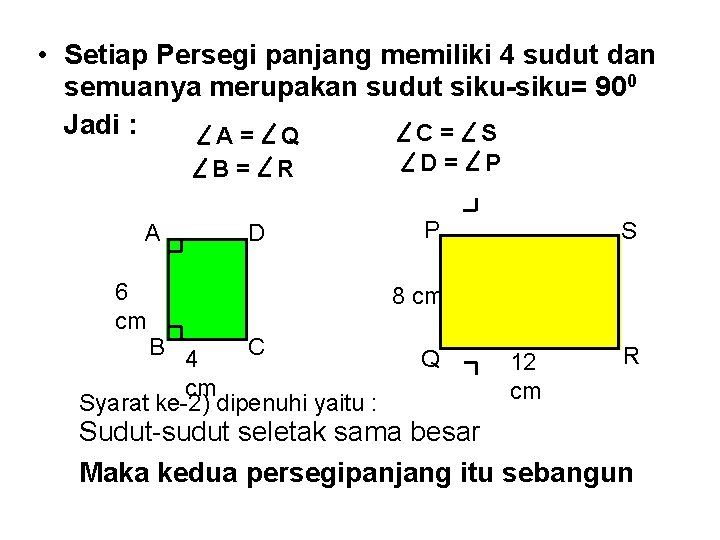
• Setiap Persegi panjang memiliki 4 sudut dan semuanya merupakan sudut siku-siku= 900 Jadi : C= S A= Q B= A 6 cm R D B 4 C cm Syarat ke-2) dipenuhi yaitu : D= P P S 8 cm Q 12 cm R Sudut-sudut seletak sama besar Maka kedua persegipanjang itu sebangun

Contoh 3 : Sebutkan benar atau salah pernyataan dibawah ini! Buat alasan dan contoh gambar serta ukurannya atas jawabanmu! 1. Semua Segi empat adalah sama bentuk. 2. Semua Persegipanjang adalah sebangun. 3. Semua Persegi adalah sebangun. 4. Semua Jajaran genjang adalah sama bentuk. 5. Semua Belah ketupat adalah sebangun. 6. Semua Trapesium adalah sebangun. 7. Semua Segitiga adalah sebangun. 8. Semua Segitiga Sama Kaki adalah sebangun. 9. Semua Segitiga Sama Sisi adalah sebangun. 10. Semua Lingkaran adalah sebangun.

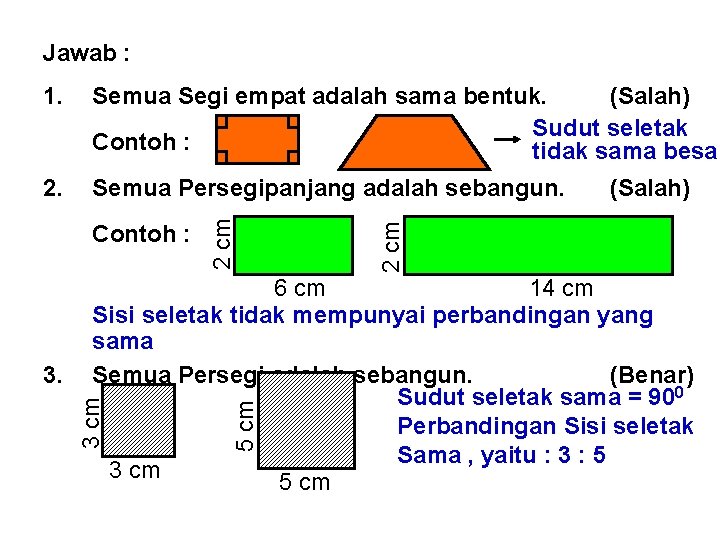
Jawab : Semua Segi empat adalah sama bentuk. (Salah) Sudut seletak Contoh : tidak sama besar 2. Semua Persegipanjang adalah sebangun. 5 cm 6 cm 14 cm Sisi seletak tidak mempunyai perbandingan yang sama Semua Persegi adalah sebangun. (Benar) Sudut seletak sama = 900 Perbandingan Sisi seletak Sama , yaitu : 3 : 5 3 cm 5 cm 3. (Salah) 2 cm Contoh : 2 cm 1.

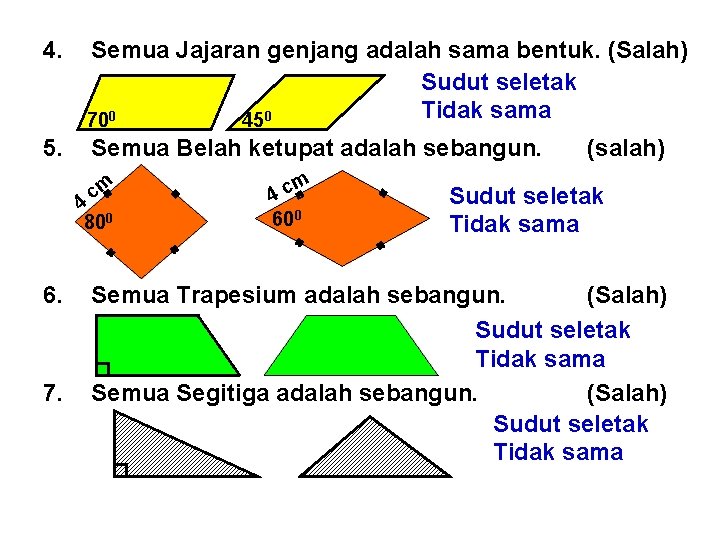
4. Semua Jajaran genjang adalah sama bentuk. (Salah) Sudut seletak Tidak sama 450 700 5. Semua Belah ketupat adalah sebangun. cm 4 800 6. 7. m 4 c 600 (salah) Sudut seletak Tidak sama Semua Trapesium adalah sebangun. (Salah) Sudut seletak Tidak sama Semua Segitiga adalah sebangun. (Salah) Sudut seletak Tidak sama

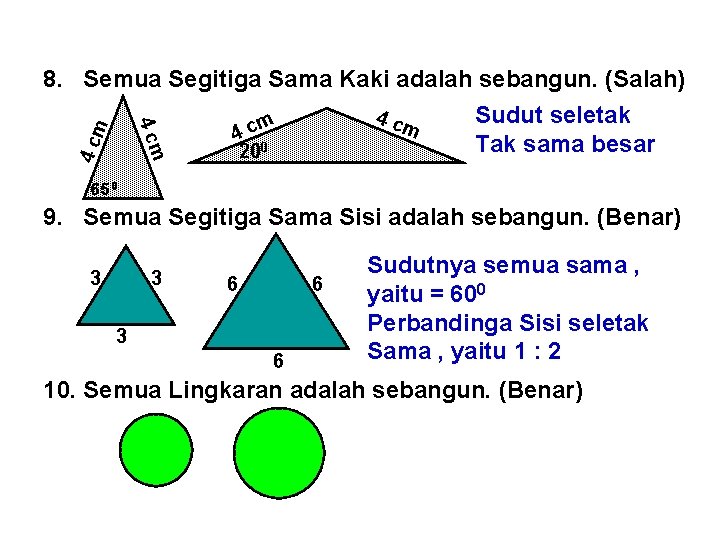
4 cm 8. Semua Segitiga Sama Kaki adalah sebangun. (Salah) 4 cm Sudut seletak m c 4 Tak sama besar 200 650 9. Semua Segitiga Sama Sisi adalah sebangun. (Benar) 3 3 6 6 3 6 Sudutnya semua sama , yaitu = 600 Perbandinga Sisi seletak Sama , yaitu 1 : 2 10. Semua Lingkaran adalah sebangun. (Benar)

C. SEGITIGA SEBANGUN Kita sudah mengetahui bahwa : Syarat kesebangunan ada dua , yaitu : (i). Sudut-sudut bersesuaian sama besar. (ii). Sisi-sisi bersesuaian mempunyai perbandingan yang sama. Apakah untuk segitiga juga seperti hal di atas ? Berikut kita akan teliti apakah seperti itu juga

Gambarlah sebuah segitiga dengan besar sudut pertama = 600 , dan sudut kedua = 400 dan buat nama segitiga itu! Pada segitiga yang kamu gambar : 1. ∠pertama = 600 , ∠kedua = 400 dan ∠ketiga =. . . 0 2. a. Sisi terpanjang (Sisi ke-1) =. . . b. Sisi yang terpendek (Sisi ke-2) =. . . c. Sisi yang satu lagi (Sisi ke-3) =. . . Jika segitiga yang kamu gambar benar , maka pada segitiga milikmu dan segitiga milik temanmu dapat dipastikan sudut-sudut yang Seletak adalah sama besar. Apakah sisi seletak pada segitiga milikmu dan milik temanmu mempunyai perbandingan yang sama? Apakah segitiga yang kamu gambar dan yang digambar temanmu sama bentuknya?

Khusus Segitiga. Dua segitiga adalah sebangun jika memenuhi satu dari : 1). Sudut seletak sama besar. atau 2). Sisi seletak mempunyai perbandingan yang sama.

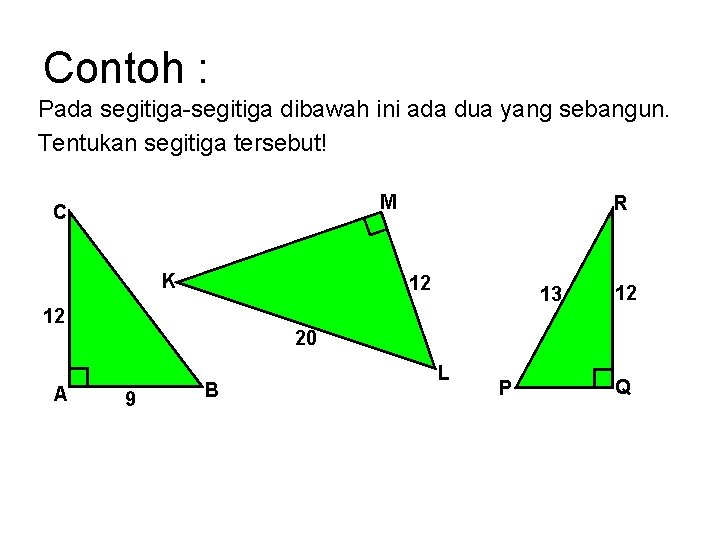
Contoh : Pada segitiga-segitiga dibawah ini ada dua yang sebangun. Tentukan segitiga tersebut! M C K R 12 13 12 12 20 A 9 B L P Q

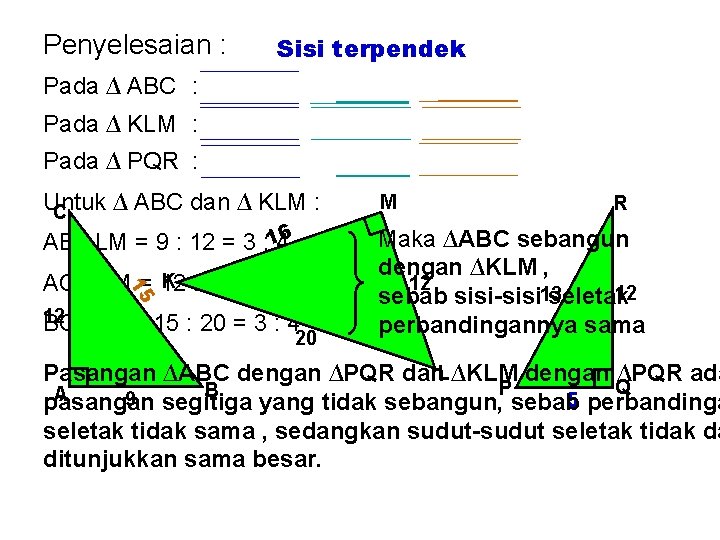
Penyelesaian : Sisi terpendek Pada ∆ ABC : AB = 9 , AC = 12 , BC = 15 Pada ∆ KLM : LM = 12 , KM = 16 , KL = 20 Pada ∆ PQR : PQ = 5 , QR = 12 , PR = 13 Untuk ∆ ABC dan ∆ KLM : C M K : 16 = 3 : 4 AC : KM = 12 Maka ∆ABC sebangun dengan ∆KLM , 12 12 sebab sisi-sisi 13 seletak perbandingannya sama AB : LM = 9 : 12 = 3 : 146 15 12 BC : KL = 15 : 20 = 3 : 4 20 R Pasangan ∆ABC dengan ∆PQR dan. L ∆KLM dengan ∆PQR ada Q P B A 9 5 pasangan segitiga yang tidak sebangun, sebab perbandinga seletak tidak sama , sedangkan sudut-sudut seletak tidak da ditunjukkan sama besar.

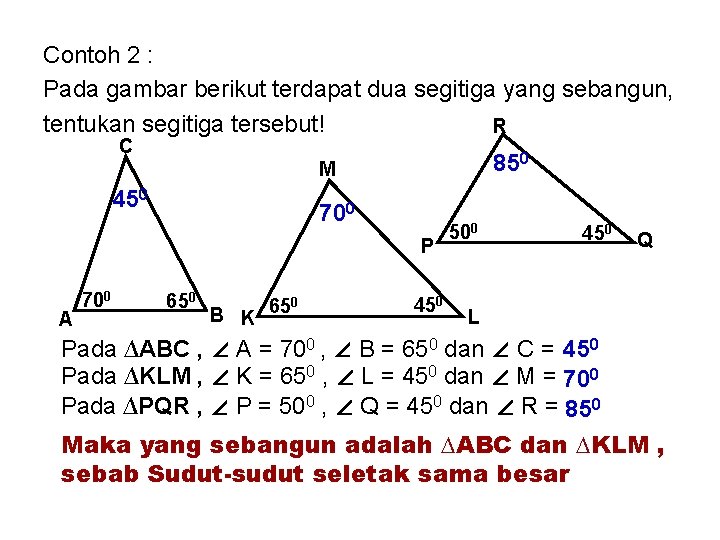
Contoh 2 : Pada gambar berikut terdapat dua segitiga yang sebangun, tentukan segitiga tersebut! R C 850 M 450 700 P A 700 650 B K 650 450 500 450 Q L Pada ∆ABC , ∠ A = 700 , ∠ B = 650 dan ∠ C = 450 Pada ∆KLM , ∠ K = 650 , ∠ L = 450 dan ∠ M = 700 Pada ∆PQR , ∠ P = 500 , ∠ Q = 450 dan ∠ R = 850 Maka yang sebangun adalah ∆ABC dan ∆KLM , sebab Sudut-sudut seletak sama besar

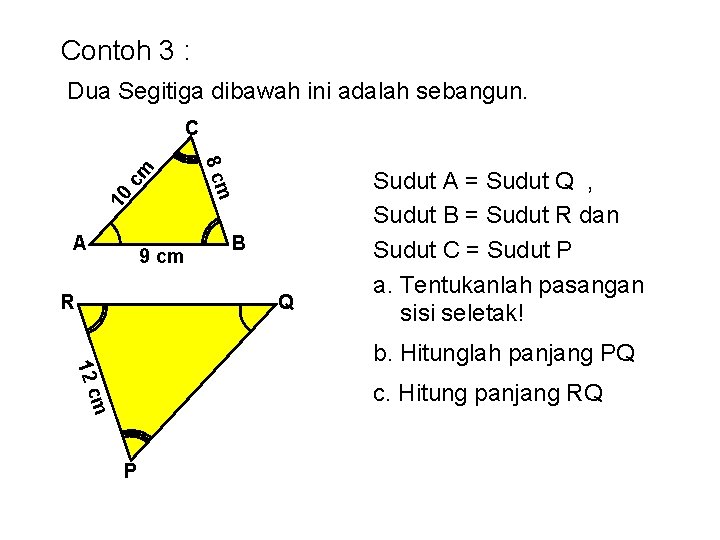
Contoh 3 : Dua Segitiga dibawah ini adalah sebangun. 10 A 9 cm R 8 cm cm C B Q Sudut A = Sudut Q , Sudut B = Sudut R dan Sudut C = Sudut P a. Tentukanlah pasangan sisi seletak! 12 c b. Hitunglah panjang PQ m c. Hitung panjang RQ P

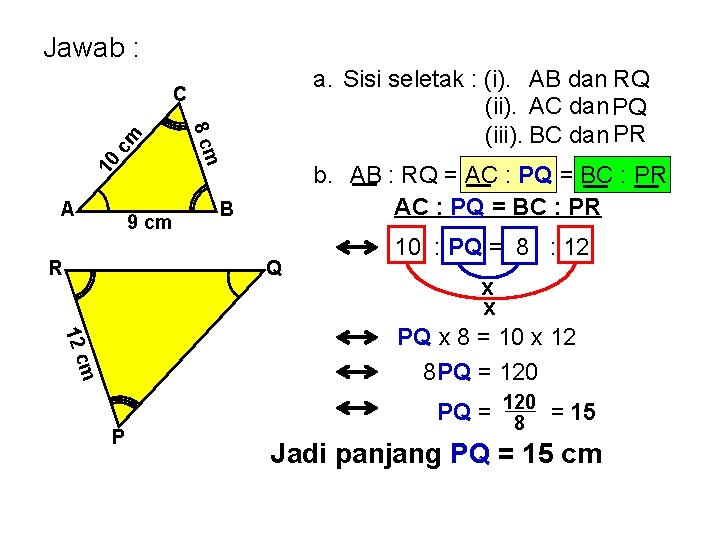
Jawab : a. Sisi seletak : (i). AB dan RQ (ii). AC dan PQ (iii). BC dan PR 10 A 9 cm R 8 cm cm C b. AB : RQ = AC : PQ = BC : PR B Q m 12 c P 10 : PQ = 8 : 12 x x PQ x 8 = 10 x 12 8 PQ = 120 8 = 15 Jadi panjang PQ = 15 cm

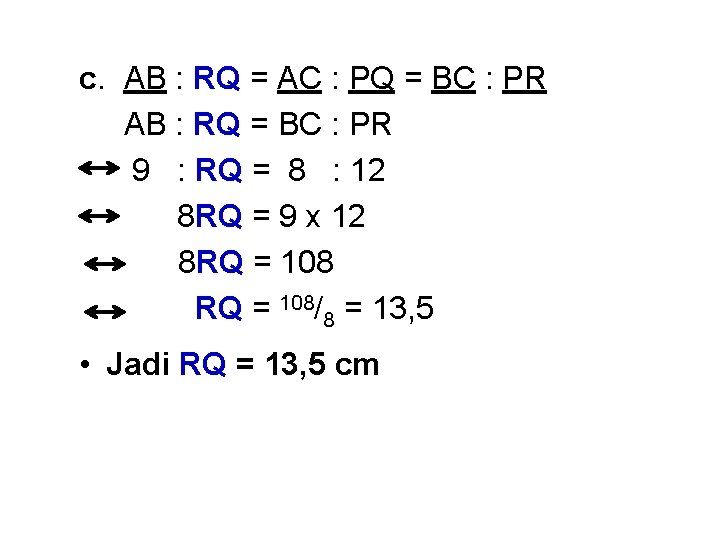
c. AB : RQ = AC : PQ = BC : PR AB : RQ = BC : PR 9 : RQ = 8 : 12 8 RQ = 9 x 12 8 RQ = 108/8 = 13, 5 • Jadi RQ = 13, 5 cm

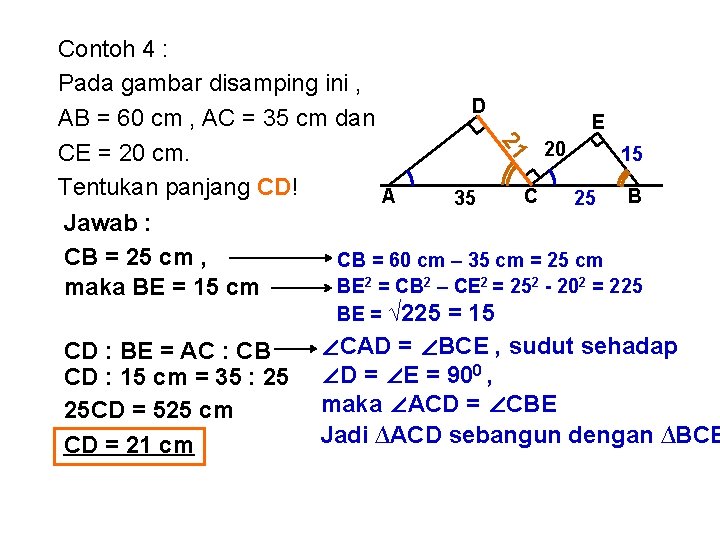
21 Contoh 4 : Pada gambar disamping ini , D AB = 60 cm , AC = 35 cm dan E 20 CE = 20 cm. 15 Tentukan panjang CD! B A C 35 25 Jawab : CB = 25 cm , CB = 60 cm – 35 cm = 25 cm BE 2 = CB 2 – CE 2 = 252 - 202 = 225 maka BE = 15 cm BE = √ 225 = 15 ∠CAD = ∠BCE , sudut sehadap CD : BE = AC : CB CD : 15 cm = 35 : 25 ∠D = ∠E = 900 , maka ∠ACD = ∠CBE 25 CD = 525 cm Jadi ∆ACD sebangun dengan ∆BCE CD = 21 cm

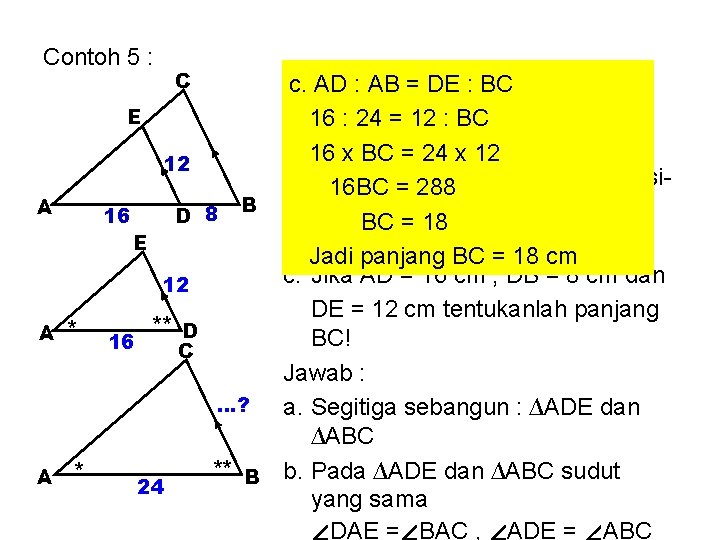
Contoh 5 : C E 12 A 16 D E 12 A A * * ** D 16 C 24 Pada di kiri c. ADGambar : AB = DE : BCini : a. 16 Sebutkan dua segitiga yang : 24 = 12 : BC sebangun. 16 x BC = 24 x 12 b. Pada dua segitiga itu tuliskan sisi 16 BC = 288 sisi 8 B BC = 18 seletak! Jadi panjang BC = 18 cm c. Jika AD = 16 cm , DB = 8 cm dan DE = 12 cm tentukanlah panjang BC! Jawab : …? a. Segitiga sebangun : ∆ADE dan ∆ABC ** B b. Pada ∆ADE dan ∆ABC sudut yang sama ∠DAE =∠BAC , ∠ADE = ∠ABC

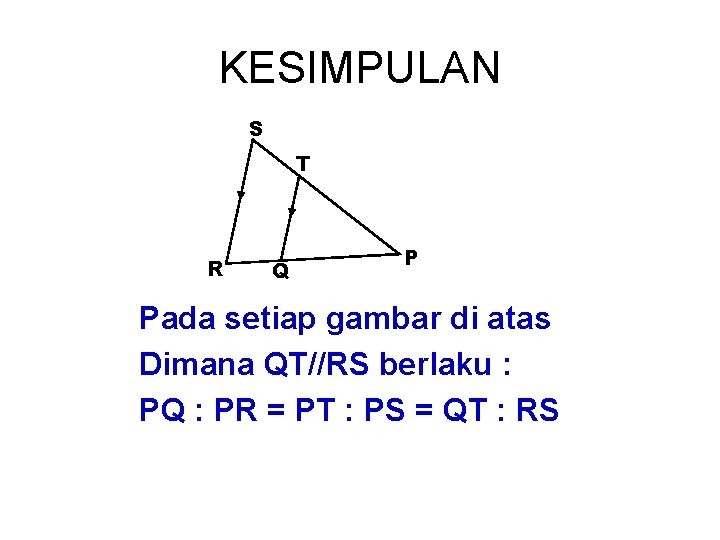
KESIMPULAN S T R Q P Pada setiap gambar di atas Dimana QT//RS berlaku : PQ : PR = PT : PS = QT : RS

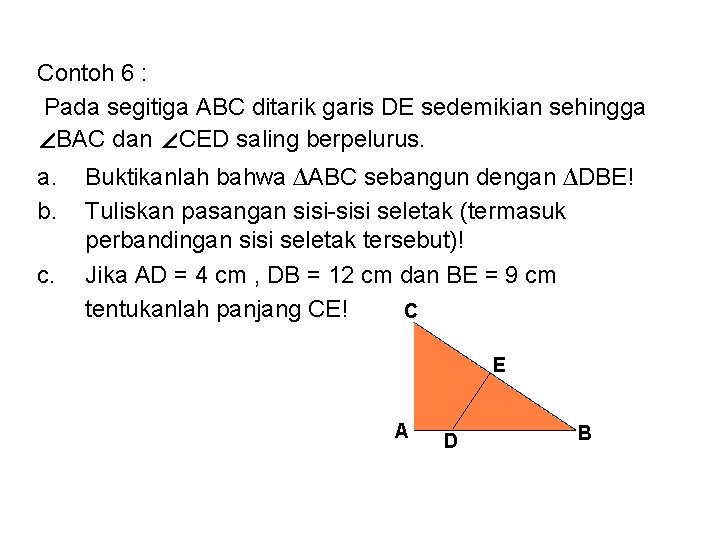
Contoh 6 : Pada segitiga ABC ditarik garis DE sedemikian sehingga ∠BAC dan ∠CED saling berpelurus. a. b. c. Buktikanlah bahwa ∆ABC sebangun dengan ∆DBE! Tuliskan pasangan sisi-sisi seletak (termasuk perbandingan sisi seletak tersebut)! Jika AD = 4 cm , DB = 12 cm dan BE = 9 cm tentukanlah panjang CE! C E A D B

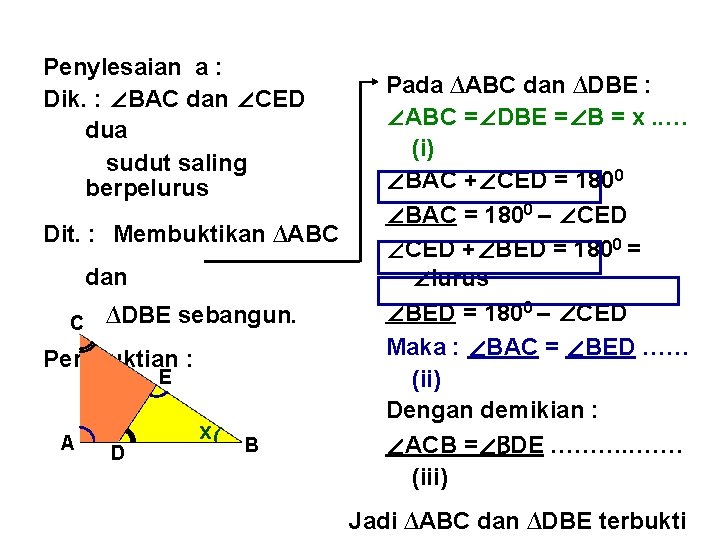
Penylesaian a : Dik. : ∠BAC dan ∠CED dua sudut saling berpelurus Dit. : Membuktikan ∆ABC dan C ∆DBE sebangun. Pembuktian : E A D x( B Pada ∆ABC dan ∆DBE : ∠ABC =∠DBE =∠B = x. . … (i) ∠BAC +∠CED = 1800 ∠BAC = 1800 – ∠CED +∠BED = 1800 = ∠lurus ∠BED = 1800 – ∠CED Maka : ∠BAC = ∠BED …… (ii) Dengan demikian : ∠ACB =∠BDE ………. . …… (iii) Jadi ∆ABC dan ∆DBE terbukti

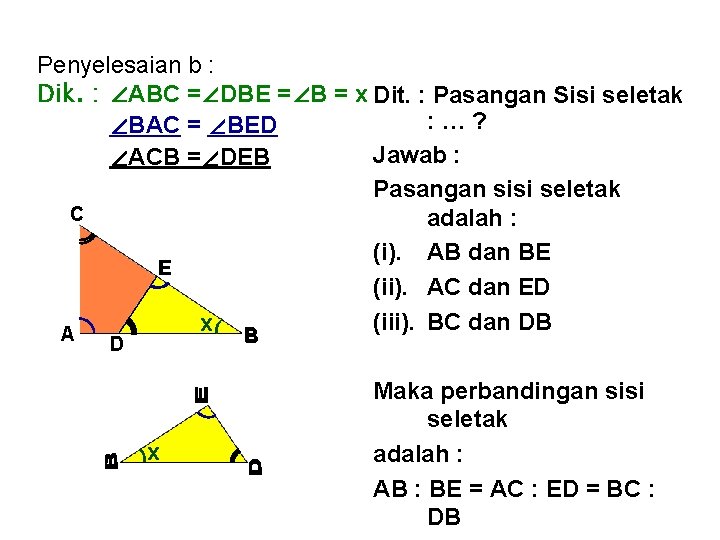
Penyelesaian b : Dik. : ∠ABC =∠DBE =∠B = x Dit. : Pasangan Sisi seletak : …? ∠BAC = ∠BED Jawab : ∠ACB =∠DEB Pasangan sisi seletak C adalah : (i). AB dan BE E (ii). AC dan ED (iii). BC dan DB x( A B D x Maka perbandingan sisi seletak adalah : AB : BE = AC : ED = BC : DB

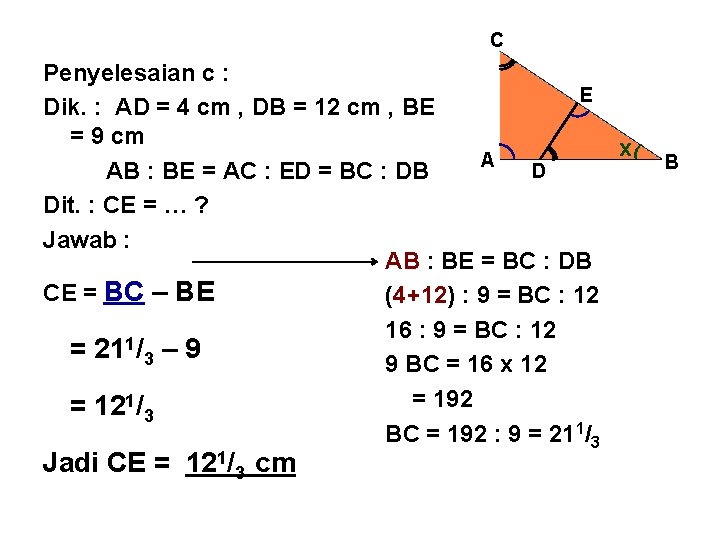
C Penyelesaian c : E Dik. : AD = 4 cm , DB = 12 cm , BE = 9 cm x( A D AB : BE = AC : ED = BC : DB Dit. : CE = … ? Jawab : AB : BE = BC : DB CE = BC – BE (4+12) : 9 = BC : 12 16 : 9 = BC : 12 1 = 21 /3 – 9 9 BC = 16 x 12 = 192 = 121/3 BC = 192 : 9 = 211/3 Jadi CE = 121/3 cm B

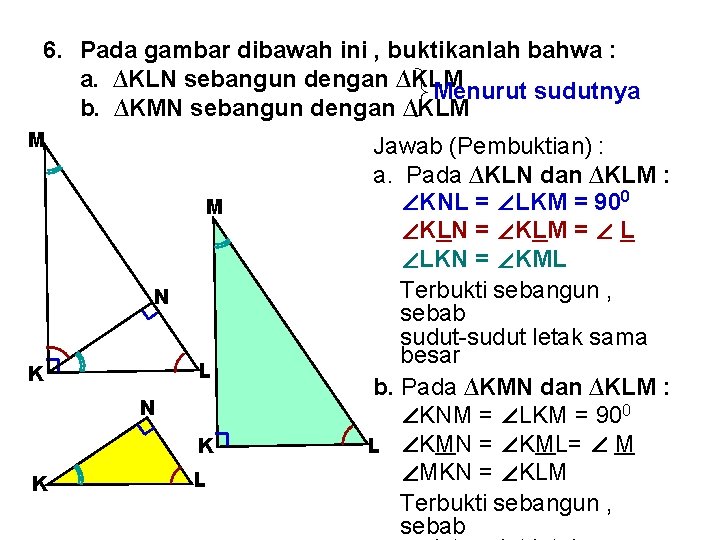
6. Pada gambar dibawah ini , buktikanlah bahwa : a. ∆KLN sebangun dengan ∆KLM Menurut sudutnya b. ∆KMN sebangun dengan ∆KLM M M N L K N K K L Jawab (Pembuktian) : a. Pada ∆KLN dan ∆KLM : ∠KNL = ∠LKM = 900 ∠KLN = ∠KLM = ∠ L ∠LKN = ∠KML Terbukti sebangun , sebab sudut-sudut letak sama besar b. Pada ∆KMN dan ∆KLM : ∠KNM = ∠LKM = 900 L ∠KMN = ∠KML= ∠ M ∠MKN = ∠KLM Terbukti sebangun , sebab

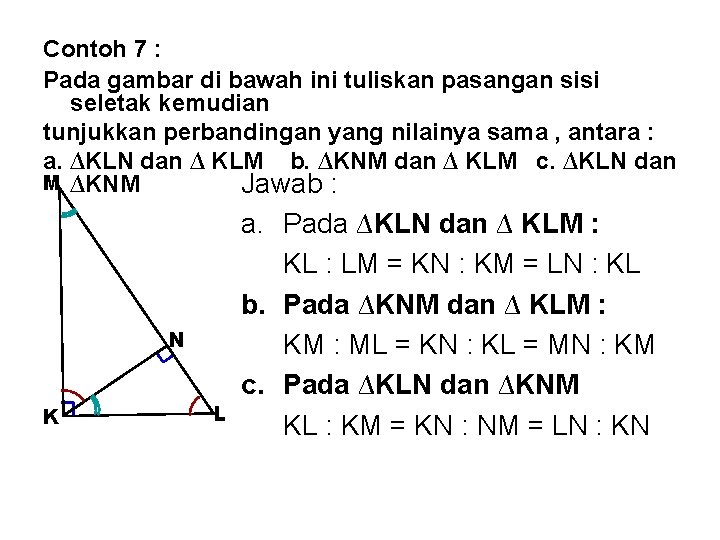
Contoh 7 : Pada gambar di bawah ini tuliskan pasangan sisi seletak kemudian tunjukkan perbandingan yang nilainya sama , antara : a. ∆KLN dan ∆ KLM b. ∆KNM dan ∆ KLM c. ∆KLN dan M ∆KNM Jawab : N K L a. Pada ∆KLN dan ∆ KLM : KL : LM = KN : KM = LN : KL b. Pada ∆KNM dan ∆ KLM : KM : ML = KN : KL = MN : KM c. Pada ∆KLN dan ∆KNM KL : KM = KN : NM = LN : KN

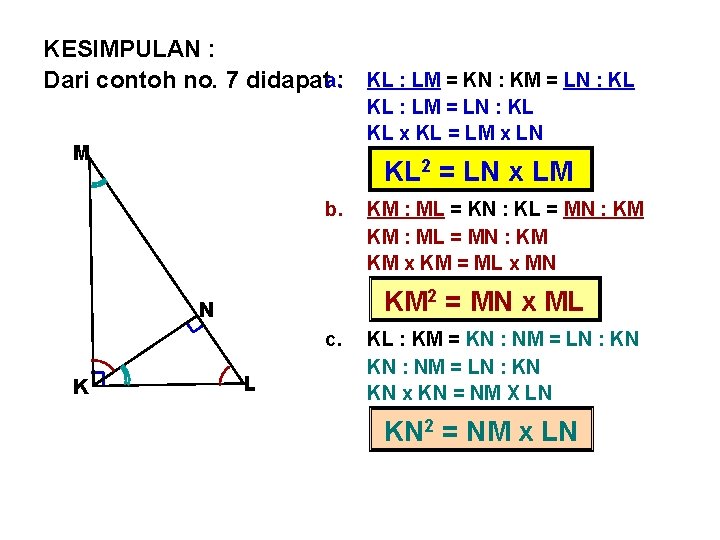
KESIMPULAN : Dari contoh no. 7 didapata. : KL : LM = KN : KM = LN : KL KL : LM = LN : KL KL x KL = LM x LN M KL 2 = LN x LM b. KM 2 = MN x ML N c. K KM : ML = KN : KL = MN : KM KM : ML = MN : KM KM x KM = ML x MN L KL : KM = KN : NM = LN : KN KN x KN = NM X LN KN 2 = NM x LN

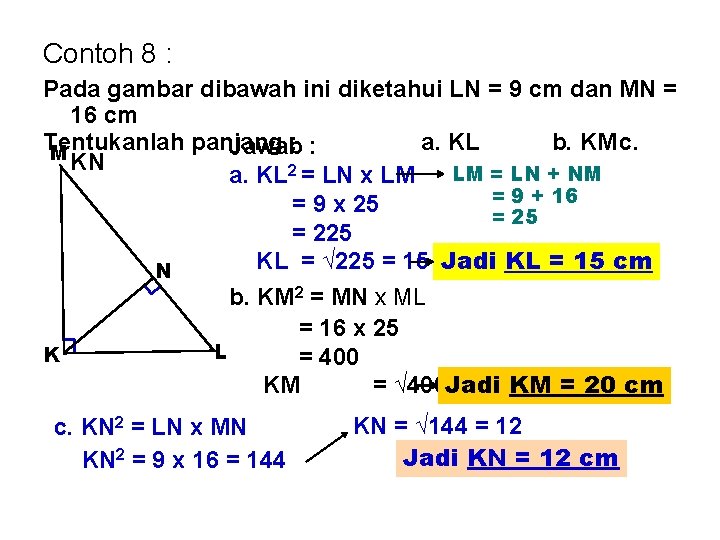
Contoh 8 : Pada gambar dibawah ini diketahui LN = 9 cm dan MN = 16 cm Tentukanlah panjang : : a. KL b. KMc. Jawab M KN LM = LN + NM a. KL 2 = LN x LM = 9 + 16 = 9 x 25 = 225 KL = √ 225 = 15 Jadi KL = 15 cm N b. KM 2 = MN x ML = 16 x 25 L K = 400 KM = √ 400 Jadi = 20 KM = 20 cm c. KN 2 = LN x MN KN 2 = 9 x 16 = 144 KN = √ 144 = 12 Jadi KN = 12 cm

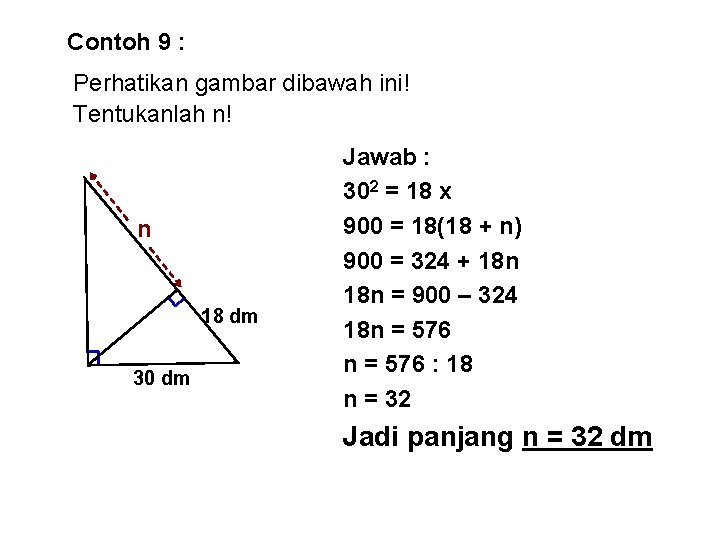
Contoh 9 : Perhatikan gambar dibawah ini! Tentukanlah n! n 18 dm 30 dm Jawab : 302 = 18 x (18 + n) 900 = 18(18 + n) 900 = 324 + 18 n = 900 – 324 18 n = 576 : 18 n = 32 Jadi panjang n = 32 dm

D. PENGGUNAAN KESEBANGUNAN

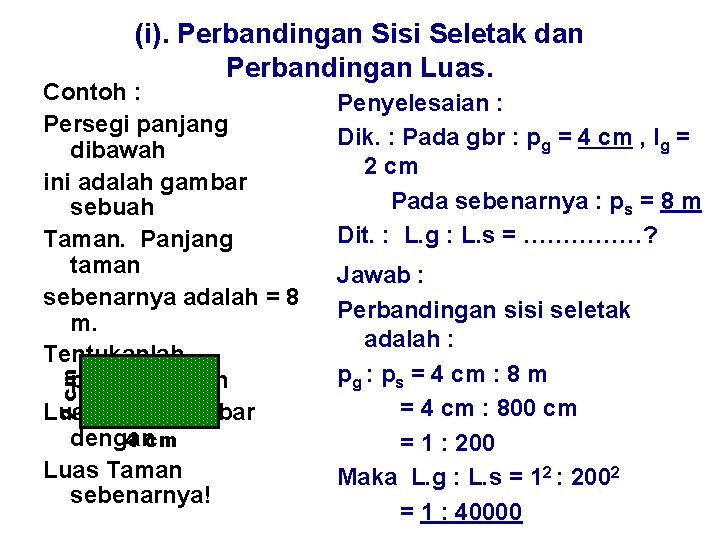
(i). Perbandingan Sisi Seletak dan Perbandingan Luas. 2 cm Contoh : Persegi panjang dibawah ini adalah gambar sebuah Taman. Panjang taman sebenarnya adalah = 8 m. Tentukanlah perbandingan Luas pada gambar dengan 4 cm Luas Taman sebenarnya! Penyelesaian : Dik. : Pada gbr : pg = 4 cm , lg = 2 cm Pada sebenarnya : ps = 8 m Dit. : L. g : L. s = ……………? Jawab : Perbandingan sisi seletak adalah : pg : ps = 4 cm : 8 m = 4 cm : 800 cm = 1 : 200 Maka L. g : L. s = 12 : 2002 = 1 : 40000

(ii). Perbandingan sisi dan Perbandingan Volum Contoh : Balok dibawah ini adalah Model Bak Air. Jika ukuran bak sebenarnya panjang = 2, 5 m , lebar 1, 5 m dan tinggi 1 m , tentukanlah perbandingan Volum model dengan sebenarnya! 2 dm 5 dm 3 dm Jawab : Misalkan pada Model : Volum = Vm , tinggi = tm Pada sebenarnya : Volum = Vs , tinggi = ts Maka : Vm : Vs = tm 3 : ts 3 = (2 dm)3 : (10 dm)3 = 13 : 5 3 = 1 : 125

Kesimpulan : Pada dua benda yang sebangun jika perbandingan sisi seletak = a : b Maka Perbandingan : (i). Luasnya = a 2 : b 2 (ii). Volumnya = a 3 : b 3 (perbandingan Volum hanya berlaku untuk bangun ruang)

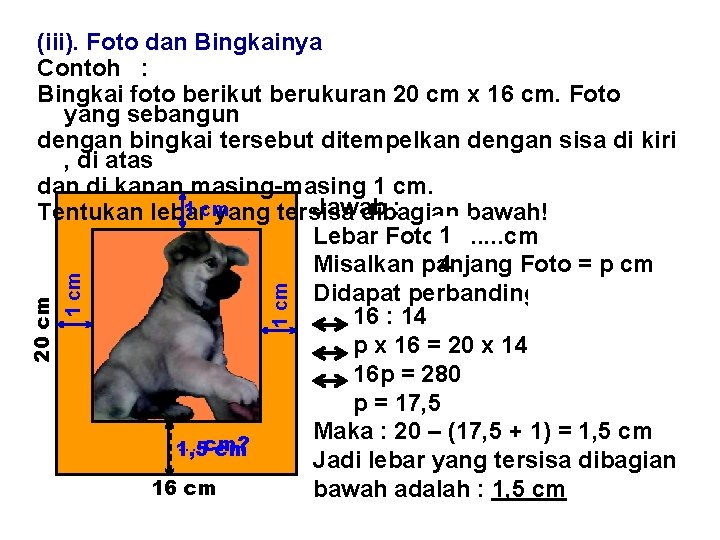
1 cm 20 cm (iii). Foto dan Bingkainya Contoh : Bingkai foto berikut berukuran 20 cm x 16 cm. Foto yang sebangun dengan bingkai tersebut ditempelkan dengan sisa di kiri , di atas dan di kanan masing-masing 1 cm. Jawab : 1 cm Tentukan lebar yang tersisa dibagian bawah! Lebar Foto 1=. . . cm 4 Misalkan panjang Foto = p cm Didapat perbandingan 20 : p = 16 : 14 p x 16 = 20 x 14 16 p = 280 p = 17, 5 Maka : 20 – (17, 5 + 1) = 1, 5 cm … cm? 1, 5 cm Jadi lebar yang tersisa dibagian 16 cm bawah adalah : 1, 5 cm

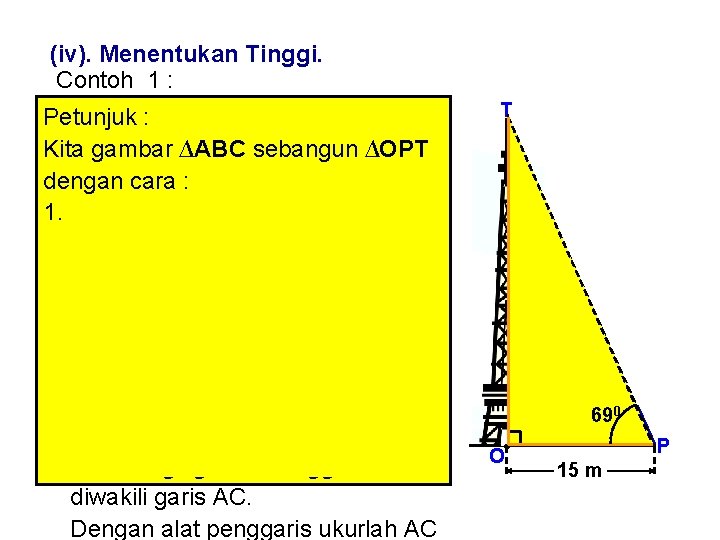
(iv). Menentukan Tinggi. Contoh 1 : Sebuah menara seperti gambar Petunjuk : disamping ini akan ditentukan Kita gambar ∆ABC sebangun ∆OPT tingginya. dengan cara. Elevasi : Jika Sudut = 690 dan jarak pengamat menara = OP =garis 15 m, 1. Gambar ke garis AB mewakili tentukanlah tinggiyang menara (OT). OP (pilih skala sesuai , misalnya 1 : 300 ) 2. Tarik garis dari B sehingga sudut B = 690 3. Tarik garis AC tegak lurus dengan AB sehingga terbentuk segitiga ABC 4. Pada Segitiga ABC tinggi menara diwakili garis AC. Dengan alat penggaris ukurlah AC T 0 69 690 O P 15 m

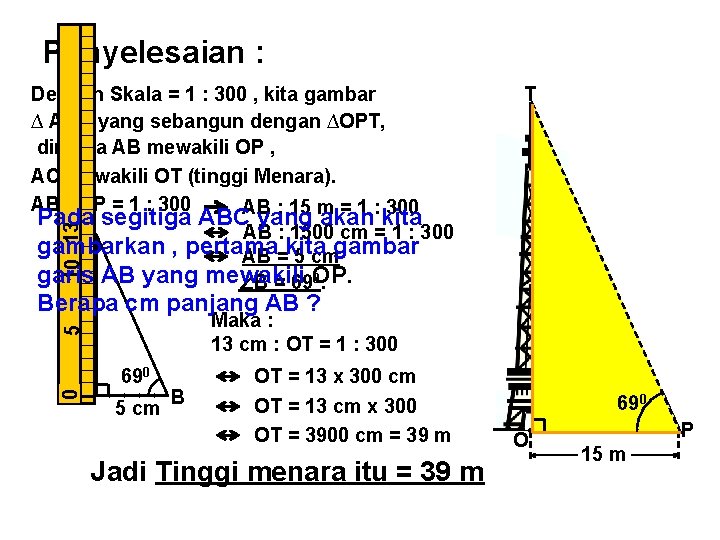
Penyelesaian : 0 Mewakili 10 13 5 menara 13 cm Dengan Skala = 1 : 300 , kita gambar ∆ ABC yang sebangun dengan ∆OPT, dimana AB mewakili OP , AC mewakili OT (tinggi Menara). AB : OP = 1 : 300 : 15 m = 1 : 300 Pada segitiga ABCAB yang akan kita AB : 1500 cm = 1 : 300 C gambarkan , pertama AB =kita 5 cmgambar garis AB yang mewakili 0. ∠B = 69 OP. T Berapa cm panjang AB ? A Maka : 13 cm : OT = 1 : 300 690 5 cm B OT = 13 x 300 cm OT = 13 cm x 300 OT = 3900 cm = 39 m Jadi Tinggi menara itu = 39 m 69 690 0 O P 15 m

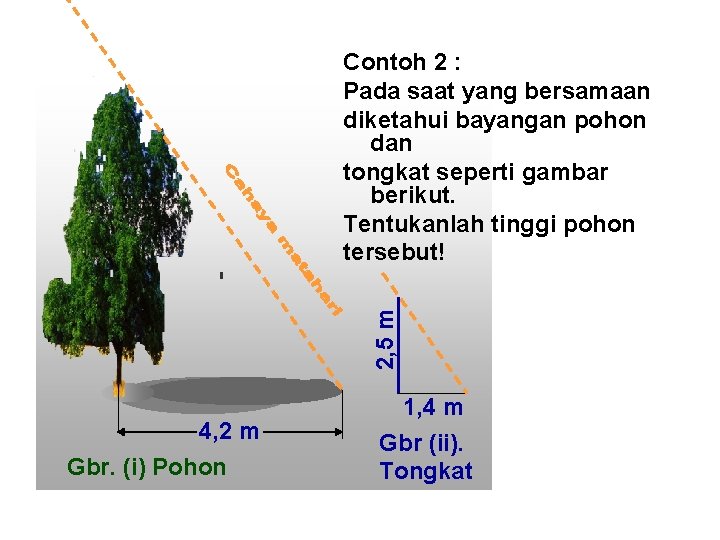
2, 5 m Contoh 2 : Pada saat yang bersamaan diketahui bayangan pohon dan tongkat seperti gambar berikut. Tentukanlah tinggi pohon tersebut! 4, 2 m Gbr. (i) Pohon 1, 4 m Gbr (ii). Tongkat

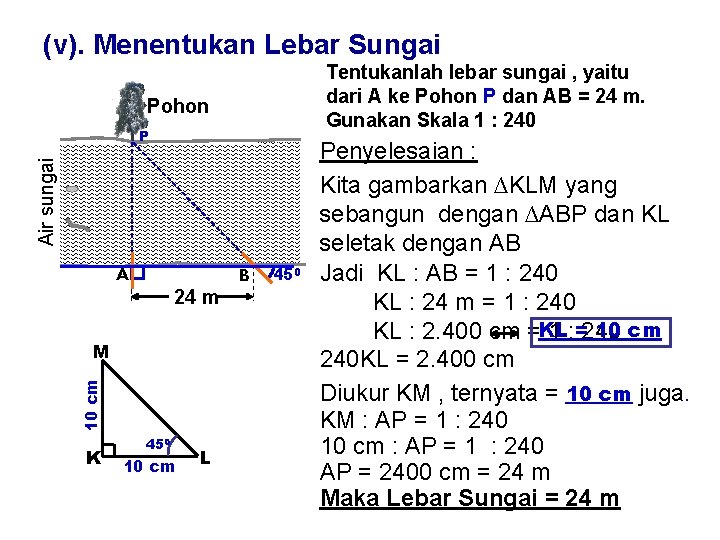
(v). Menentukan Lebar Sungai Tentukanlah lebar sungai , yaitu dari A ke Pohon P dan AB = 24 m. Gunakan Skala 1 : 240 Pohon Air sungai P A 24 m 10 cm M K 450 10 cm L B 450 Penyelesaian : Kita gambarkan ∆KLM yang sebangun dengan ∆ABP dan KL seletak dengan AB Jadi KL : AB = 1 : 240 KL : 24 m = 1 : 240 10 cm KL : 2. 400 cm =KL 1 : =240 240 KL = 2. 400 cm Diukur KM , ternyata = 10 cm juga. KM : AP = 1 : 240 10 cm : AP = 1 : 240 AP = 2400 cm = 24 m Maka Lebar Sungai = 24 m

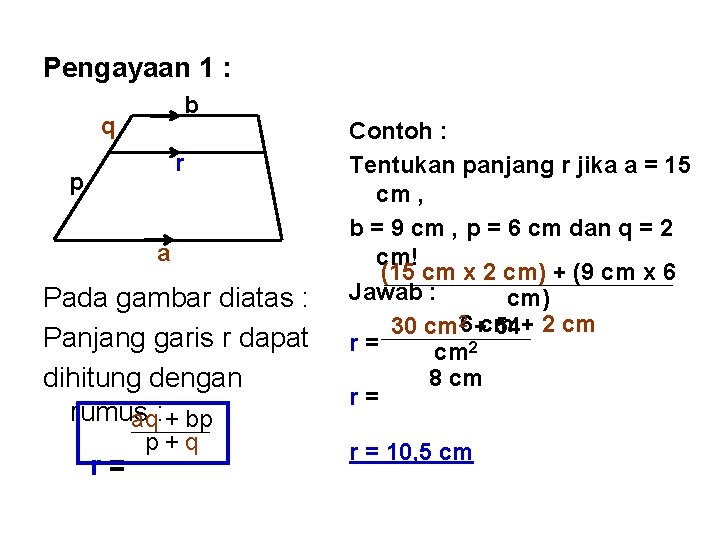
Pengayaan 1 : b q r p a Pada gambar diatas : Panjang garis r dapat dihitung dengan rumus aq: + bp r= p+q Contoh : Tentukan panjang r jika a = 15 cm , b = 9 cm , p = 6 cm dan q = 2 cm! (15 cm x 2 cm) + (9 cm x 6 Jawab : cm) 30 cm 26 +cm 54+ 2 cm r= cm 2 8 cm r= r = 10, 5 cm

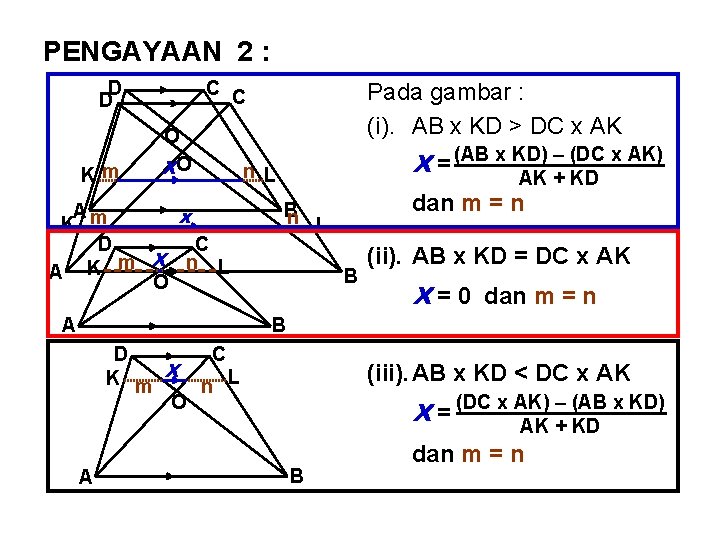
PENGAYAAN 2 : D D Km C C O XO A x K m D C m X n L A K O Pada gambar : (i). AB x KD > DC x AK – (DC x AK) X = (AB x KD) AK + KD n L dan m = n B n L B (ii). AB x KD = DC x AK X = 0 dan m = n B A D C K m X n L O A (iii). AB x KD < DC x AK – (AB x KD) X = (DC x AK) AK + KD B dan m = n

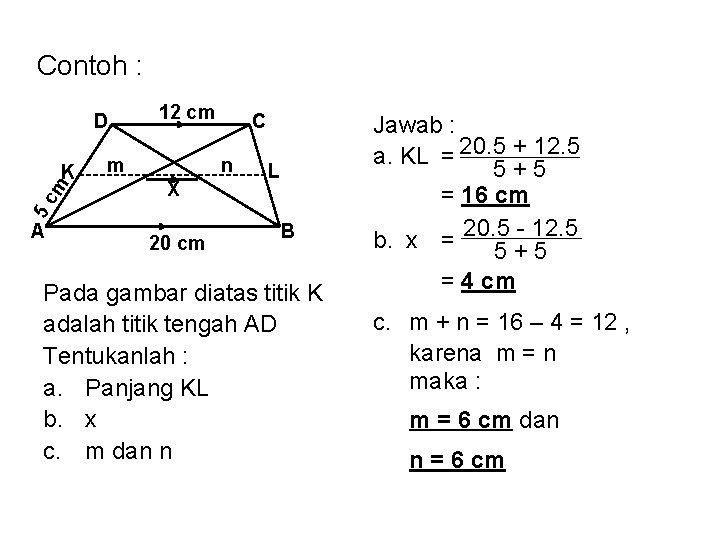
Contoh : D 5 c m K A 12 cm m C n X 20 cm L B Pada gambar diatas titik K adalah titik tengah AD Tentukanlah : a. Panjang KL b. x c. m dan n Jawab : a. KL = 20. 5 + 12. 5 5+5 = 16 cm 20. 5 - 12. 5 b. x = 5+5 = 4 cm c. m + n = 16 – 4 = 12 , karena m = n maka : m = 6 cm dan n = 6 cm

Indikator Pokok pada Kesebangunan 1. Menyebutkan Syarat Kesebangunan suatu benda pada umumnya. 2. Menyebutkan Syarat Kesebangunan khusus segitiga. 3. Menentukan sisi yang bersesuaian berdasarkan sudut yang diketahui pada suatu benda. 4. Menentukan Sudut yang sama besar berdasarkan sisi seletak. 5. Penggunaan Skala pada kesebangunan. 6. Menentukan Perbandingan sisi seletak. 7. Menggunakan aturan kesebangunan untuk menyelesaikan suatu masalah. 8. Menyebutkan Syarat kongruensi.

1. Syarat kesebangunan pada umumnya : Dua benda adalah sebangun jika pasangan-pasangan sisi yang sesuai antara kedua benda itu perbandingannya yang sama dan pasangan-pasangan sudut yang sesuai sama besarnya. 2. Syarat kesebangunan khusus segitiga : Dua segitiga adalah sebangun jika pada kedua segitiga itu ditemukan salah satu syarat kesebangunan pada umumnya. Sebab : • • Pada dua segitiga apabila sisi yang sesuai perbandingannya sama , dengan sendirinya pasangan sudut yang sesuai pasti sama besar. Sebaliknya , jika pasangan sudut yang sesuai sama besar dengan sendirinya pasangan sisi yang sesuai pasti perbandingannya sama.

• Dua benda adalah kongruen apabila bentuknya sama serta ukurannya sama.

Kesimpulan • Pada gambar seperti disamping C E A D B

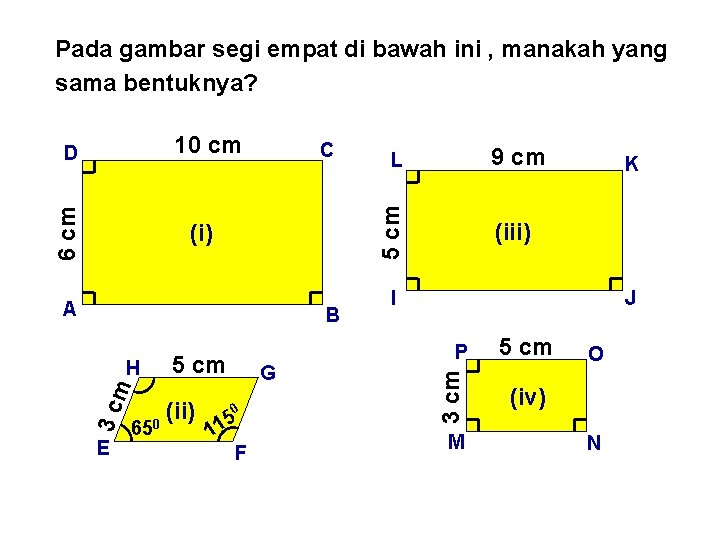
Pada gambar segi empat di bawah ini , manakah yang sama bentuknya? 10 cm C A B m 3 c E 65 5 cm (ii) 0 G 0 5 11 F K (iii) I J P 3 cm (i) H 9 cm L 5 cm 6 cm D M 5 cm O (iv) N