lohy teorie graf RNDr Ji Dvok CSc dvorakuai

Úlohy teorie grafů RNDr. Jiří Dvořák, CSc. dvorak@uai. fme. vutbr. cz Teorie systémů a operační analýza 1

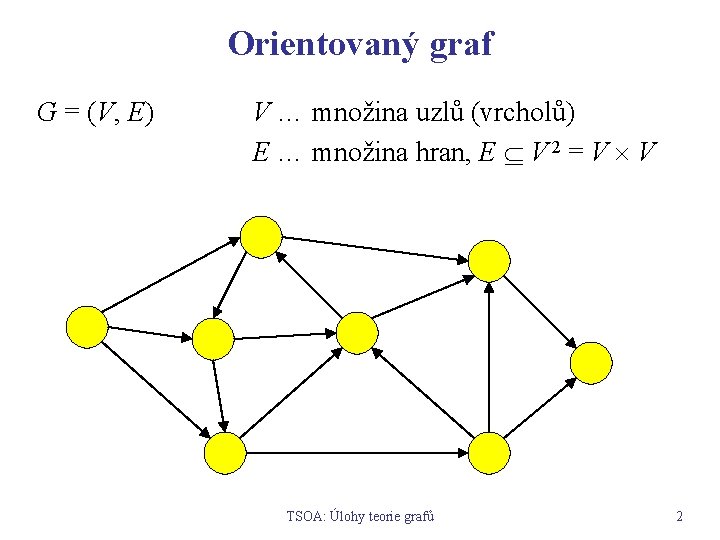
Orientovaný graf G = (V, E) V … množina uzlů (vrcholů) E … množina hran, E V 2 = V V TSOA: Úlohy teorie grafů 2

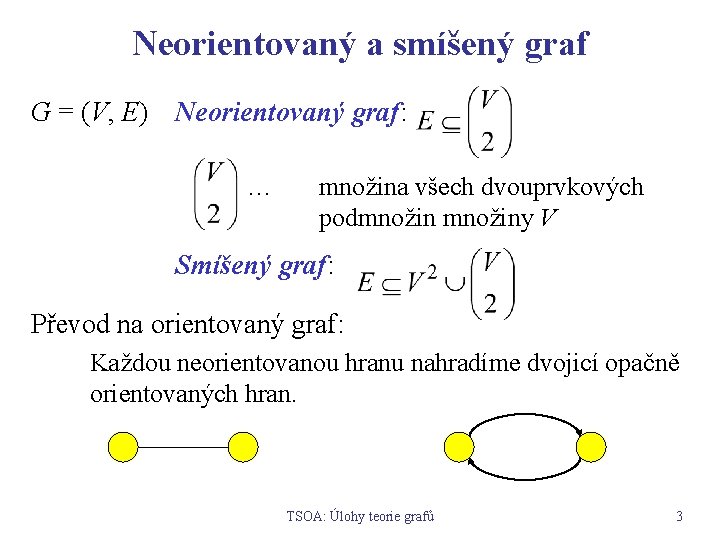
Neorientovaný a smíšený graf G = (V, E) Neorientovaný graf: … množina všech dvouprvkových podmnožiny V Smíšený graf: Převod na orientovaný graf: Každou neorientovanou hranu nahradíme dvojicí opačně orientovaných hran. TSOA: Úlohy teorie grafů 3

Sled a cesta Orientovaný sled je posloupnost uzlů propojených hranami se stejnou orientací. Tedy posloupnost {i 1 , i 2 , … , ik }, kde ij V, tvoří orientovaný sled, jestliže (ij , ij+1) E pro všechna j = 1, …, k – 1. Sled je posloupnost uzlů propojená hranami bez ohledu na jejich orientaci. Tah je sled, ve kterém se neopakuje žádná hrana. Cesta je sled, ve kterém se neopakuje žádný uzel. Orientovaný tah (orientovaná cesta) je tah (cesta), kde všechny hrany mají shodnou orientaci. Graf se nazývá souvislý, jestliže mezi každými jeho dvěma uzly existuje sled. Orientovaný graf se nazývá silně souvislý, jestliže z každého uzlu existují orientované sledy do všech ostatních uzlů. TSOA: Úlohy teorie grafů 4

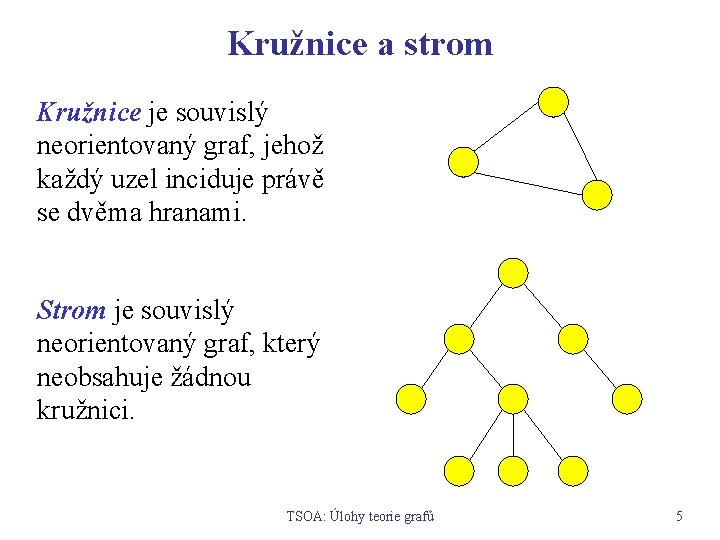
Kružnice a strom Kružnice je souvislý neorientovaný graf, jehož každý uzel inciduje právě se dvěma hranami. Strom je souvislý neorientovaný graf, který neobsahuje žádnou kružnici. TSOA: Úlohy teorie grafů 5

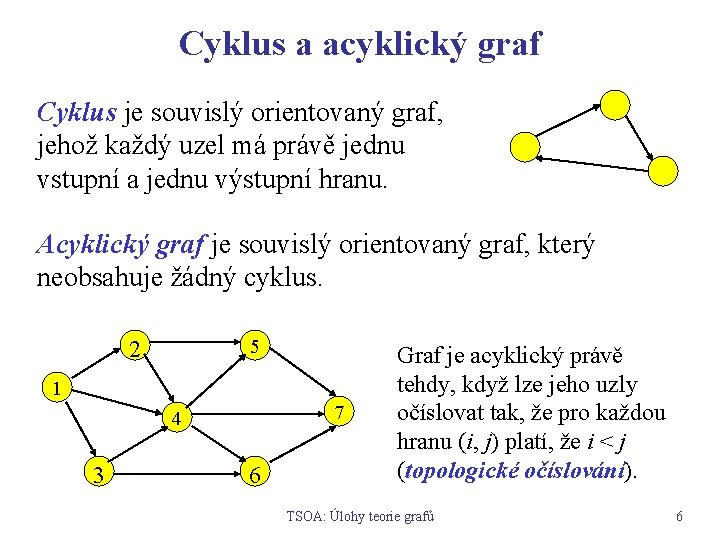
Cyklus a acyklický graf Cyklus je souvislý orientovaný graf, jehož každý uzel má právě jednu vstupní a jednu výstupní hranu. Acyklický graf je souvislý orientovaný graf, který neobsahuje žádný cyklus. 5 2 1 7 4 3 6 Graf je acyklický právě tehdy, když lze jeho uzly očíslovat tak, že pro každou hranu (i, j) platí, že i < j (topologické očíslování). TSOA: Úlohy teorie grafů 6

Algoritmus topologického očíslování 1. Položme G 1 = G a k = 1. 2. V grafu Gk najdeme uzel, který nemá žádné vstupní hrany a přidělíme mu číslo k. Pokud takový uzel neexistuje, znamená to, že graf G není acyklický a postup končí. 3. Z grafu Gk vytvoříme graf Gk+1 tak, že z něj vypustíme uzel s číslem k a všechny hrany, které z tohoto uzlu vystupují. 4. Je-li graf Gk+1 neprázdný, položíme k = k+1 a vrátíme se k bodu 2. V opačném případě postup končí (všechny uzly se podařilo topologicky očíslovat a graf G je tedy acyklický). TSOA: Úlohy teorie grafů 7

Ohodnocený graf Uzlové ohodnocení: a: V R Příklady interpretace: doba, zisk, náklady, kapacita, spolehlivost, … Hranové ohodnocení: c: E R Příklady interpretace: délka, doba, zisk, náklady, kapacita, spolehlivost, … TSOA: Úlohy teorie grafů 8

Tok v síti od zdroje ke spotřebiči Mějme orientovaný graf G = (V, E), uzly z, s V, z s a nezáporné hranové ohodnocení c, přičemž z je zdroj, s je spotřebič a c(i, j) = cij je kapacita hrany (i, j). Tok od zdroje ke spotřebiči je libovolné hranové ohodnocení x splňující podmínky: 0 x(i, j) c(i, j) pro vš. (i, j) E, Velikost toku = TSOA: Úlohy teorie grafů 9

Úloha nalezení maximálního toku od zdroje ke spotřebiči Maximalizovat za podmínek Speciální metoda řešení: Ford - Fulkersonův algoritmus TSOA: Úlohy teorie grafů 10

Řez v síti Mějme orientovaný graf G = (V, E), uzly z, s V, z s, přičemž z je zdroj a s je spotřebič. Nechť Vs a Vz jsou množiny uzlů takové, že z Vz , s Vs , Vz Vs = V. Řezem v síti nazveme množinu hran Kapacita řezu je rovna součtu kapacit jeho hran: Ford - Fulkersonova věta: Maximální tok od zdroje ke spotřebiči se rovná kapacitě minimálního řezu, tj. TSOA: Úlohy teorie grafů 11

Ford - Fulkersonův algoritmus Algoritmus vychází z nějakého přípustného toku x. I. Hledání cesty ze zdroje do spotřebiče. Hledáme neorientovanou cestu ze zdroje do spotřebiče, na níž by bylo možno zvětšit tok, a přitom provádíme označování uzlů. Je-li možno tok na hraně (i, j) resp. na hraně (j, i) zvětšit resp. zmenšit o hodnotu j , označíme uzel j dvojicí (+i , j ) resp. (–i , j ). Jestliže se podaří výše uvedenou cestu najít, pokračujeme etapou II. V opačném případě je aktuální tok maximální a postup končí. II. Zvětšení toku. Na cestě nalezené v předchozí etapě provedeme zvětšení toku a vracíme se na etapu I. TSOA: Úlohy teorie grafů 12

I. Hledání cesty Na počátku jsou všechny uzly neoznačeny. 1. Uzel z označíme dvojicí (+z, ) a považujeme jej za otevřený. 2. Vybereme libovolný otevřený označený uzel i, uzavřeme jej a provedeme následující operace: · Každý neoznačený uzel j, který je bezprostředním následníkem uzlu i a pro nějž je xij < cij , otevřeme a označíme jej dvojicí (+i , j ), kde j = min { i , cij – xij}. · Každý neoznačený uzel j, který je bezprostředním předchůdcem uzlu i a pro nějž je xji > 0, otevřeme a označíme jej dvojicí (–i , j ), kde j = min { i , xji}. 3. Opakujeme krok 2 až do označení uzlu s (pak přecházíme na krok 4) nebo do vyčerpání všech označených otevřených uzlů (pak je tok x maximální, přičemž množiny označených a neoznačených uzlů určují odpovídající minimální řez). TSOA: Úlohy teorie grafů 13

II. Zvětšení toku 4. Položíme j = s, = s. 5. Je-li uzel j označen dvojicí (+i , j ), pak zvětšíme tok hranou (i, j) o hodnotu . Je-li uzel j označen dvojicí (–i , j ), pak zmenšíme tok hranou (j, i) o hodnotu . 6. Je-li i z, položíme j = i a vracíme se na krok 5. V opačném případě je zvětšení toku ukončeno. Zrušíme označení všech uzlů a vracíme se na krok 1. TSOA: Úlohy teorie grafů 14

Délka cesty a vzdálenost v orientovaném hranově ohodnoceném grafu Délka cesty je dána součtem délek hran, tvořících cestu. (Orientovaná) vzdálenost z uzlu i do uzlu j: d(i, j) = délka nejkratší (orientované) cesty z uzlu i do uzlu j. Jestliže neexistuje (orientovaná) cesta z uzlu i do uzlu j, klademe d(i, j) = . Pozn. : V dalším textu budeme pod pojmy vzdálenost a cesta chápat orientovanou vzdálenost a orientovanou cestu. TSOA: Úlohy teorie grafů 15

Úloha nalezení nejkratší cesty Minimalizovat za podmínek kde cij je délka hrany (i, j). Optimální řešení (pokud existuje) obsahuje hodnoty xij = 1, jestliže hrana (i, j) leží na nejkratší cestě, a xij = 0 v opačném případě. TSOA: Úlohy teorie grafů 16

Vlastnosti vzdálenosti v grafu Jestliže graf neobsahuje cykly záporné délky, pak: n Pro všechny trojice uzlů i, j, k platí trojúhelníková nerovnost d(i, j) d(i, k) + d(k, j) n Pro každou dvojici různých vrcholů i, j platí Bellmanovy rovnice TSOA: Úlohy teorie grafů 17

Speciální algoritmy pro hledání nejkratších cest Předpokládejme, že graf neobsahuje cykly záporné délky. Pak je možno použít speciální algoritmy pro hledání nejkratších cest, které jsou založeny na předcházejících vlastnostech vzdálenosti v grafu (tj. na trojúhelníkové nerovnosti resp. na Bellmanových rovnicích). Dále uvedeme algoritmy, které jsou schopny najít nejkratší cesty (pokud existují) z nějakého uzlu s do všech ostatních uzlů grafu. Předpokládejme, že uzly grafu jsou očíslovány přirozenými čísly. Označme symbolem ps(i) bezprostředního předchůdce uzlu i na nejkratší cestě z uzlu s do uzlu i. Údaje ps(i) určují nejkratší cesty z uzlu s do libovolného uzlu grafu. Je-li ps(i) = – 1, znamená to, že cesta z uzlu s do uzlu i neexistuje. Pro uzel s klademe ps(s) = 0. TSOA: Úlohy teorie grafů 18

Algoritmus pro libovolné ohodnocení hran 1. Polož d(s, s) = 0, ps(s) = 0 a pro každý uzel i s polož d(s, i) = , ps(i) = – 1. 2. Procházej hrany grafu v libovolném pořadí. Jestliže pro hranu (i, j) E je d(s, j) > d(s, i) + c(i, j), pak polož d(s, j) = d(s, i) + c(i, j), ps(j) = i. 3. Jestliže pro všechny hrany (i, j) E již platí, že d(s, j) d(s, i) + c(i, j), pak postup končí. TSOA: Úlohy teorie grafů 19

Algoritmus pro nezáporné ohodnocení hran Označme symbolem D množinu uzlů, o nichž víme, že hodnota d(s, k) je již definitivní. 1. Polož d(s, s) = 0, ps(s) = 0 a pro každý uzel i s polož d(s, i) = , ps(i) = – 1. Dále polož D = {s}, k = s. 2. Prozkoumej všechny hrany (k, j) E, pro něž j D. Jestliže d(s, j) > d(s, k) + c(k, j), pak polož d(s, j) = d(s, k) + c(k, j), ps(j) = k. 3. Je-li D = V, pak konec (byly nalezeny cesty do všech vrcholů). V opačném případě najdi uzel k D takový, že d(s, k) = min {d(s, j) | j D}. 4. Je-li d(s, k) = , pak konec (žádný další vrchol již není dostupný z vrcholu s). V opačném případě zařaď vrchol k do množiny D a pokračuj krokem 2. TSOA: Úlohy teorie grafů 20

Algoritmus pro acyklický graf Předpokládáme, že uzly jsou očíslovány topologicky čísly od 1 do n. 1. Polož d(s, s) = 0, ps(s) = 0 a pro každý uzel i s polož d(s, i) = , ps(i) = – 1. 2. Pro j = s+1, … , n proveď : 2. 1 Jestliže uzel j má nějaké bezprostřední předchůdce, pak polož 2. 2 Jestliže d(s, j) < , pak polož ps(j) = i*, kde i* je takové, že d(s, j) = d(s, i*) + c(i*, j). TSOA: Úlohy teorie grafů 21