Formaln axiomatick teorie Teorie relac Teorie Formln teorie

Formalní axiomatické teorie Teorie relací

Teorie • Formální teorie je dána – Jazykem • formální jazyk prvořádové teorie je jazyk důkazového kalkulu (množina dobře utvořených formulí – DUF) – Množinou axiomů • je podmnožinou DUF a skládá se z: – množiny logických axiomů (logicky pravdivé) – množiny speciálních axiomů (pravdivé v zamýšlené interpretaci) – Množinou dedukčních pravidel • množina dedukčních pravidel daného kalkulu • Formální teorie je množina všech formulí, které lze dokázat z axiomů teorie. Teorie relací 2

Teorie • Důkaz formule A v teorii T (T| A) je posloupnost kroků (DUF) takových, že: – poslední krok je formule A – každý krok důkazu je buď • logický axiom nebo • speciální axiom nebo • formule získána aplikací dedukčního pravidla na některou z předchozích formulí posloupnosti • Hilbertův kalkul a přirozená dedukce jsou speciální typy teorií (bez speciálních axiomů, pouze logické axiomy a korektní ded. pravidla) => dokazovat lze pouze logicky pravdivé formule. Teorie relací 3

Teorie • Nejdůležitější teorie – Teorie aritmetiky • Robinsonova aritmetika (Q), Peanova aritmetika (PA) – viz: minulá přednáška – Teorie relací • teorie uspořádání • teorie ekvivalence • Atd. – Algebraické teorie • teorie grup, okruhů a těles • teorie svazů • Atd. Teorie relací 4

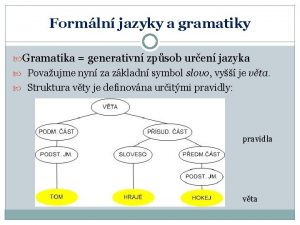
Teorie ostrého uspořádání • Teorie ostrého uspořádání verze 1: speciální znaky: =, < binární predikáty – Logické axiomy: axiomy Hilbertova kalkulu – Speciální axiomy: • • • O 1. x (x = x) O 2. x y [(x=y) (y=x)] O 3. x y z [(x=y y=z) (x=z)] O 4. x y z [(x=y x<z) (y<z)] O 5. x y z [(x=y z<x) (z<y)] O 6. x y [(x<y) (y<x)] O 7. x y z [(x<y y<z) (x<z)] O 8. x y [x=y x<y y<x] O 9. x y [x<y] O 10. x y [y<x] O 11. x y [x<y z [x<z z<y]] Teorie relací reflexivita symetrie transitivita asymetrie transitivita 5

Teorie ostrého uspořádání • Teorie ostrého uspořádání verze 2 – speciální znaky =, < – Logické axiomy: axiomy Hilbertova kalkulu – Speciální axiomy: • • • V 1. x y [x<y (y<x)] V 2. x y z [(x<y y<z) x<z] V 3. x y [x=y x<y y<x] V 4. x y [x<y] V 5. x y [y<x] V 6. x y [x<y z [x<z z<y]] binární predikáty asymetrie transitivita Teorie rovnosti: O 1 -O 3 Teorie ostrého uspořádání (O 1 -O 7) nebo (V 1 -V 2) Teorie lineárního ostrého uspořádání: O 1 -O 8 nebo V 1 -V 3 Teorie hustého uspořádání: O 1 -O 11 nebo V 1 -V 6 Teorie relací 6

Příklady, modely • Teorie rovnosti (ekvivalence) – O 1. x (x = x) reflexivita – O 2. x y [(x=y) (y=x)] symetrie – O 3. x y z [(x=y y=z) (x=z)] transitivita Každá teorie T definuje množinu svých modelů, tj. interpretací, ve kterých jsou pravdivé axiomy teorie („teorie v kostce“). Příklad modelů: 1. Universum = množina přirozených čísel – 2. Universum = množina přirozených čísel – 3. Symbol ‘=‘ je interpretován jako relace „být stejné hmotnosti“ Universum = množina DUF jazyka PL 1 – 6. Symbol ‘=‘ je interpretován jako relace „být stejně vysoký“ Universum = množina individuí – 5. Symbol ‘=‘ je interpretován jako relace „modulo 5“ (mít stejný zbytek po dělení 5) Universum = množina individuí – 4. Symbol ‘=‘ je interpretován jako identita čísel. Symbol ‘=‘ je interpretován jako relace ekvivalence formulí (tj. mít přesně stejné modely) atd. Teorie relací 7

Příklady, modely • Teorie ostrého uspořádání – – V 1. x y [x<y (y<x)] asymetrie V 2. x y z [(x<y y<z) x<z] transitivita Příklady modelů: 1. Universum = množina přirozených čísel • 2. Symbol ‘<‘ je interpretován jako relace ostře menší (<) Universum = potenční množina 2 M (kde M je libovolná množina, např. individuí) • 3. Symbol ‘<‘ je interpretován jako relace (být vlastní podmnožinou) Universum = množina individuí • Symbol ‘<‘ je interpretován jako relace „být potomkem“

Příklady, modely • Pro každou relaci R, která splňuje axiomy ostrého uspořádání, platí, že R je: – Ireflexivní (žádný prvek není v relaci sám se sebou) – Asymetrická (je-li R(a, b) pak není R(b, a)) – Transitivní • Důkaz, že ostré uspořádání je ireflexivní (rezoluční metodou): A 1: x y [x<y (y<x)] (asymetrie) ------------------- x (x<x) (ireflexivita) x (x<x) A 1 x y [ (x<y) (y<x)] 1. (x<y) (y<x) 3. (a<a) 4. (a<a) 1. , 3. x/a, y/a 5. # 3. , 4. Negovaný závěr je ve sporu s předpokladem, tedy původní závěr vyplývá, tedy v dané teorii je platná ireflexivita. Teorie relací 9

Příklady, modely • Pro každou relaci R, která splňuje axiomy ireflexivity a transitivity, platí, že R je asymetrická: – Tedy ostré uspořádání opravdu stačí definovat pouze dvěma z výše uvedených tří axiomů (transitivita je nutná, + ireflexivita nebo asymetrie) • Důkaz (rezoluční metodou): A 1: x (x<x) ireflexivita A 2: x y z [(x<y y<z) x<z] transtitivita ------------------- x y [(x<y) (y<x)] asymetrie důkaz rezoluční metodou: 1. (x<x) 2. (x<y) (y<z) (x<z) 3. (a<b) negovaný 4. (b<a) závěr + skolemizace 5. (b<z) (a<z) 2. , 3. : x/a, y/b 6. (a<a) 4. , 5. : z/a 7. Spor 1. , 6. : x/a Negovaný závěr je ve sporu s předpoklady, tedy původní závěr vyplývá.

Částečné (neostré) uspořádání • Teorie částečného uspořádání – speciální znaky: binární predikát – Logické axiomy: axiomy Hilbertova kalkulu – Speciální axiomy: • PO 1. x (x x) • PO 2. x y [((x y) (y x)) x=y] • PO 3. x y z [((x y) (y z)) (x z)] reflexivita anti-symetrie transitivita ‘=’ znak pro identitu Každá struktura U, R , která je modelem této teorie, se nazývá částečně uspořádaná množina. Příklady: – N, , kde N je množina přirozených čísel a je relace menší nebo rovno na číslech. – 2 M, , kde 2 M je množina všech podmnožin dané množiny M a je relace být (vlastní či nevlastní) podmnožinou Teorie relací 11

Quasi uspořádání • Někdy se stává, že chceme zavést částečné uspořádání R na množině M, ale relace R není antisymetrická. Potom můžeme využít teorii quasi uspořádání: – speciální znaky: binární predikát – Logické axiomy: axiomy Hilbertova kalkulu – Speciální axiomy: • PO 1. x (x x) • PO 3. x y z [((x y) (y z)) (x z)] reflexivita transitivita Struktura U, R , která je modelem této teorie, kde relace R není antisymetrická, se nazývá quasi-uspořádaná množina. Příklad: U = množina všech DUF, kde relace R je definována jako: F 1, F 2 DUF, R(F 1, F 2) =df F 2 |= F 1 Tato relace není asymetrická, neboť, je-li F 2 |= F 1 a F 1 |= F 2, pak jsou sice formule F 1, F 2 ekvivalentní, F 1 F 2 (mají stejné modely), ale není pravda, že jsou identické. Např. formule p q, p q jsou ekvivalentní, ale nejsou to identické formule. Teorie relací 12

Teorie ekvivalence – speciální znaky: binární predikát – Logické axiomy: axiomy Hilbertova kalkulu – Speciální axiomy: • Ek 1. x (x x) reflexivita • Ek 2. x y [((x y) (y x))] symetrie • Ek 3. x y z [((x y) (y z)) (x z)] transitivita Příklad modelu: relace ekvivalence nad množinou DUF, kde F 1 F 2 právě když (F 1, F 2 DUF, F 1 |= F 2 |= F 1) Teorie relací 13

Rozklad na množině Jestliže máme quasi-uspořádanou množinu <M, >, a relace není antisymetrická, pak můžeme částečně uspořádat dle množinu ekvivalenčních tříd, neboť každá ekvivalence definuje rozklad na množině M: • Definice: rozklad na množině A je množina X = { Xi ; i I } taková že: • Xi A pro i I (Xi jsou vzájemně disjunktní • Xi Xj = Ø pro i, j I, i j podmnožiny A) • Xi = A (sjednocení Xi pokrývá celou A) Xi – třídy rozkladu • Definice: Nechť je relace ekvivalence na množině A. Nechť [x] = {y A; y x}. Pak A/ = {[x]; x A} se nazývá faktorová množina množiny A podle ekvivalence . • Věta: Množina A/ je rozklad na množině A. Teorie relací 14

Faktorová množina, rozklad [1] [3] [4] [0] {x; x 0} [1] {x; x 1} [2] {x; x 2} [2] [3] {x; x 3} [4] {x; x 4}

Rozklad na množině: příklad • Definujeme relaci ekvivalence 5 (modulo 5) na množině celých čísel Z takto ( 5 Z Z): 5 = {(x, y); 5 dělí x-y }. (Ověřte, že je to ekvivalence!) • Pak Z/ 5 {[0], [1], [2], [3], [4]}, kde [0] = {…-5, 0, 5, 10, 15, …} [1] = {…-9, -4, 1, 6, 11, …} [2] = {. . . -8, -3, 2, 7, 12, 17, . . . } [3] = {. . . -7, -2, 3, 8, 13, 18, . . . } [4] = {. . . -6, -1, 4, 9, 14, 19, . . . } Je rozklad na množině Z. Teorie relací 16

Částečné uspořádání faktorové množiny • Příklad (pokračování): • Definujeme částečné uspořádání 5 na množině Z/ 5 z předchozího příkladu: • [x] [y] iff (x/5)zb (y/5)zb, kde (i/5)zb= r a i=k*5+r; x, y je libovolný reprezentant dané třídy. • Důkaz, že definice je korektní (nesmí záviset na výběru reprezentantů): – – [x]=[x’], [y]=[y’] a [x] [y] pak musí být [x’] [y’]: Je-li [x]=[x’], pak x=k*5 + r 1, x’=k’*5 + r 1 Je-li [y]=[y’], pak y=l*5 + r 2, y’=l’*5 + r 2 Tedy [x] [y] iff [r 1] [r 2] iff [x’] [y’]. • Důkaz, že takto definovaná relace je částečným uspořádáním – cvičení.

Teorie relací, shrnutí příkladů • quasi uspořádání 1. „množiny X a Y jsou v relaci, pokud |X| |Y| (kardinalita X je menší nebo rovna kardinalitě Y) 2. relace dělitelnosti na množině celých čísel 3. „nebýt starší“ na množině lidí • částečné uspořádání – relace množinové inkluze ( ) na množině množin – relace dělitelnosti na množině přirozených čísel – relace částečného uspořádání nad množinou DUF/ , kdy F 1, F 2 DUF, [F 1] [F 2] právě když F 2 |= F 1 • ekvivalence – relace ekvivalence na množině DUF, kdy F 1, F 2 DUF, F 1 F 2 právě když F 1 |= F 2 a F 2 |= F 1. Teorie relací 18

Teorie relací • Obecně speciální axiomy zapisujeme ve tvaru: – – – x R(x, x) x y [R(x, y) R(y, x)] x y z [(R(x, y) R(y, x)) x=y)] x y z [(R(x, y) R(y, z)) R(x, z)] reflexivita i-reflexivita symmetrie anti-symentrie transitivita • R je zde binární relace a víme, že každý speciální axiom je pravdivý v zamýšlené interpretaci. • Ani jeden speciální axiom však není logicky pravdivá formule! (Snadné ověření v libovolném korektním kalkulu) Teorie relací 19

Dokazování v teorii • Dokazování v teorii – teorie je budována nad kalkulem, tedy samotné dokazování se provádí v daném kalkulu, kdy jako předpoklady klademe speciální axiomy teorie – Např. : Mějme teorii T={reflexivita, transitivita} • dokažte, že v dané teorii platí symetrie x R(x, x) x y z [(R(x, y) R(y, z)) R(x, z)] ---- x y [R(x, y) R(y, x)] Teď již záleží nad jakým kalkulem (rezoluční, přirozená dedukce, Hilbertův kalkul) svou teorii budujeme a podle toho ověřujeme logickou platnost úsudku. Teorie relací 20

Dokazování v teorii x R(x, x) x y z[(R(x, y) R(y, z)) R(x, z)] ---- x y [R(x, y) R(y, x)] K důkazu použijeme rezoluční metodu 1. R(x, x) 2. R(x’, y’) R(y’, z’) R(x’, z’) 3. R(a, b) 4. R(b, a) 5. R(a, y’) R(y’, b) 6. R(a, b) 7. # x R(x, x) x y z[ R(x, y) R(y, z) R(x, z)] x y[R(x, y) R(y, x)] 2. , 4. x’/b, z’/a 1. , 5. x/a, y’/a Rezoluční metodou jsme dokázali, že negovaný závěr je ve sporu s předpoklady, tedy původní nenegovaný závěr log. vyplývá, tedy úsudek je platný. Teorie relací 21

Teorie funkcí • Funkce jako relace – každá n-ární funkce je (n+1)-ární relace F: a b c ([R(a, b) R(a, c)] b=c) Parciální F: ke každé n-tici prvků a M. . . M existuje nanejvýš jeden prvek b M. – pokud vezmeme formuli F jako speciální axiom, tak můžeme hovořit o teorii funkcí – příklady: modely budou interpretace splňující tuto formuli (R můžeme interpretovat jako relaci, kdy 2. prvek každé dvojice je výsledek po dělení prvků dvojice a. ) { 1, 1 , 2, 1 , 2 , 2, 2 , 1 , …, 4, 2 , …} Teorie relací 22

Teorie funkcí • Funkce jako relace Totální funkce F: A B: Ke každému prvku a A existuje právě jeden prvek b B takový, že F(a)=b: a b F(a, b) a b c [(F(a, b) F(a, c)) b=c] Modelem této teorie tedy bude interpretace splňující danou formuli (danou relaci F můžeme interpretovat jako množinu všech dvojic, kdy 2. prvek je následníkem prvku a), funkce sčítání, násobení, … Teorie relací 23

Teorie funkcí • Funkce (zobrazení) • • Zobrazení f : A B je surjekce (zobrazení A na B), jestliže k libovolnému b B existuje a A takový, že f(a)=b. b [B(b) a (A(a) F(a, b))]. Zobrazení f : A B je injekce (prosté zobrazení A do B), jestliže pro všechna a A, b A taková, že a b platí, že f(a) f(b). a b [(A(b) A(a) (a b)) c d (F(a, c) F(b, d) c d)]. Zobrazení f : A B je bijekce (prosté zobrazení A na B), jestliže f je surjekce a injekce. Teorie relací 24

Isomorfismus vzhledem k relaci R • Definice (isomorfní množiny): – Uspořádané množiny (A, 1), (B, 2) se nazývají isomorfní, jestliže existuje bijekce f: A B taková, že • x, y A: x 1 y právě když f(x) 2 f(y) Například množiny N a množina sudých kladných čísel jsou isomorfní vzhledem k uspořádání čísel dle velikosti – existuje funkce f (např. 2 x) Dále bude isomorfismus nad (DUF/ , ), kde, F 1, F 2 DUF, F 1 F 2 právě když F 2 |= F 1 a funkce f bude identita. Teorie relací 25

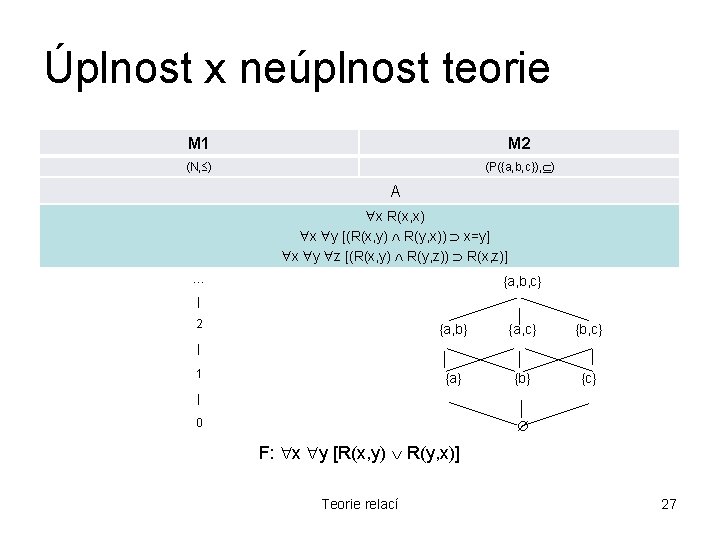
Úplnost x neúplnost teorie Definice: teorie T je úplná, právě když rozhoduje každou formuli F, tj. T | F nebo T | F Zároveň víme, že pro (např. ) Hilbertův kalkul platí silná věta o úplnosti kalkulu (neplést úplnost teorie s úplností kalkulu!): A | F T | F, kde A je množina speciálních axiomů teorie T. Tedy teorie dokazuje vše, co z ní vyplývá. Je-li teorie T neúplná, pak existují nezávislé sentence F (které T nerozhoduje). Pak ovšem F nemůže vyplývat z T. Tedy existuje model M teorie T, ve kterém F není pravdivá. Proto, V případě, že existují aspoň 2 neisomorfní modely (M 1, M 2) dané teorie T, pak existuje aspoň jedna nezávislá sentence F, pro níž platí: M 1| A a M 1| F, M 2| A a M 2| F, pak je tato teorie T neúplná. Teorie relací 26

Úplnost x neúplnost teorie M 1 M 2 (N, ) (P({a, b, c}), ) A x R(x, x) x y [(R(x, y) R(y, x)) x=y] x y z [(R(x, y) R(y, z)) R(x, z)] … {a, b, c} | 2 {a, b} {a, c} {b, c} {a} {b} {c} | 1 | 0 F: x y [R(x, y) R(y, x)] Teorie relací 27

Úplnost x neúplnost teorie Obecně: Pokud je teorie úplná, pak má všechny modely vzájemně izomorfní (vzhledem k axiomům teorie) • Teorie částečného uspořádání je neúplná. • Teorie lineárního uspořádání je úplná. Teorie relací 28