Linern funkce Rozdlen linernch funkc Popis jednotlivch funkc

Lineární funkce • Rozdělení lineárních funkcí • Popis jednotlivých funkcí

Jméno autora: Marie Roglová Škola: ZŠ Náklo Datum vytvoření (období): únor 2013 Ročník: 9. Tematická oblast: Matematické dovednosti Téma: Lineární funkce - úvod Metodický list (anotace): seznámení se s pojmem funkce, rozdělení funkcí, grafy funkcí

Funkce - definice Funkce je předpis, který každému číslu z definičního oboru, který je podmnožinou množiny všech reálných čísel R, přiřazuje právě jedno reálné číslo. Funkci značíme obvykle písmenem f, a obvykle zapisujeme ve tvaru: y = f(x) , např. y = 2 x+1 nebo ve tvaru: f: y = 2 x + 1

Zápis funkce f: y = 2 x + 1 kde proměnná x je nezávisle proměnná y je závisle proměnná Nezávislost je dána tím, že její hodnotu můžeme libovolně měnit, ovšem jen v rámci definované množiny, definičního oboru. Množina všech hodnot x, tedy všechny hodnoty, kterých může proměnná x pro danou funkci nabývat, se nazývá definiční obor. Značí se: D(f)

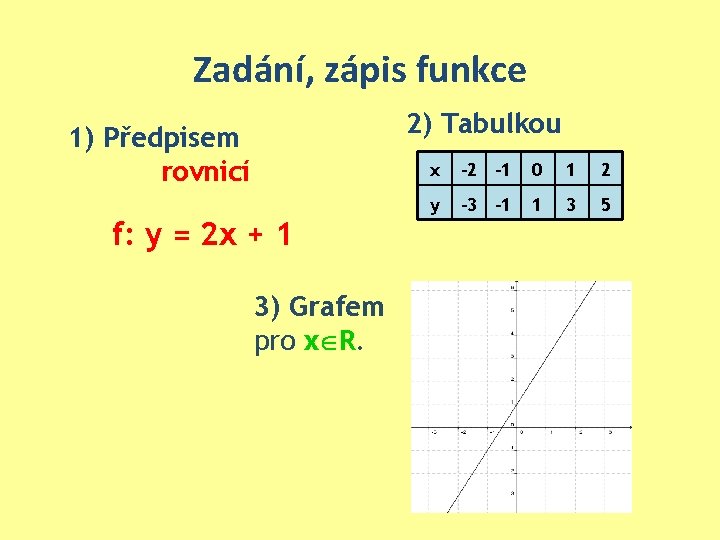
Zadání, zápis funkce 2) Tabulkou 1) Předpisem rovnicí f: y = 2 x + 1 3) Grafem pro x R. x -2 -1 0 1 2 y -3 -1 1 3 5

Lineární funkce Obecná rovnice lineární funkce y = a. x + b kde a, b jsou libovolná reálná čísla a definičním oborem množina všech reálných čísel. y 3 = 5 + x y = 2 x y = - 5 x +3 y = 0, 5 x - 1 +1 y x 2 = 5 , 0 –

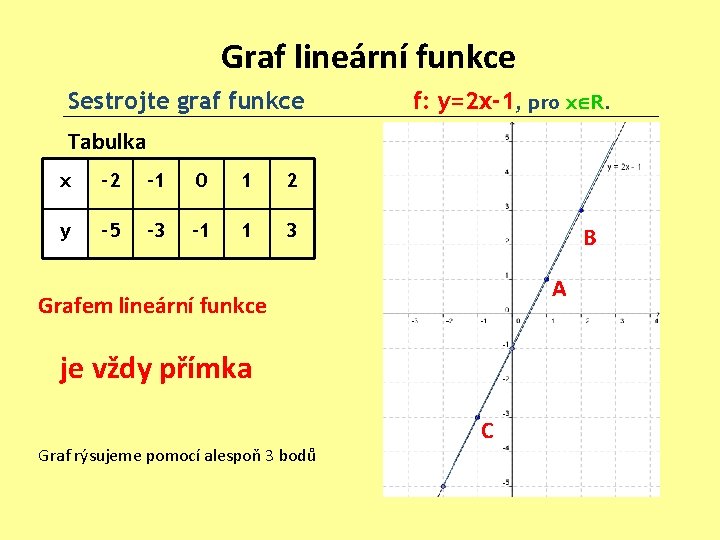
Graf lineární funkce Sestrojte graf funkce f: y=2 x-1, pro x R. Tabulka x -2 -1 0 1 2 y -5 -3 -1 1 3 B A Grafem lineární funkce je vždy přímka Graf rýsujeme pomocí alespoň 3 bodů C

Na zakreslení odpovídající přímky do soustavy souřadnic nám stačí souřadnice dvou bodů, ale pro kontrolu používáme souřadnice tří bodů. Není-li zadáno jinak, je definiční obor i obor hodnot množina všech reálných čísel: D(f) = R - osa x H(f) = R - osa y Kdy každému bodu osy x je přiřazen právě jeden bod osy y

Lineární funkce Jiný zápis lineární funkce obecným vzorcem: y = k. x + q kde k a q jsou libovolná čísla (koeficienty)

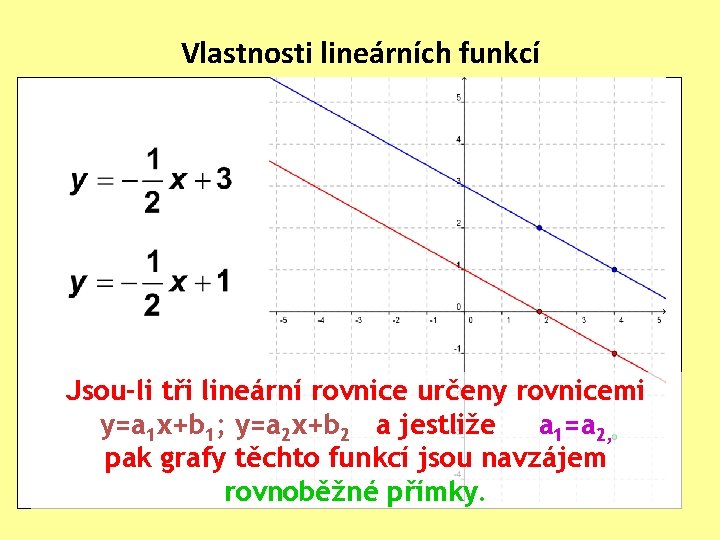
Vlastnosti lineárních funkcí Jsou-li tři lineární rovnice určeny rovnicemi y=a 1 x+b 1; y=a 2 x+b 2 a jestliže a 1=a 2, pak grafy těchto funkcí jsou navzájem rovnoběžné přímky.

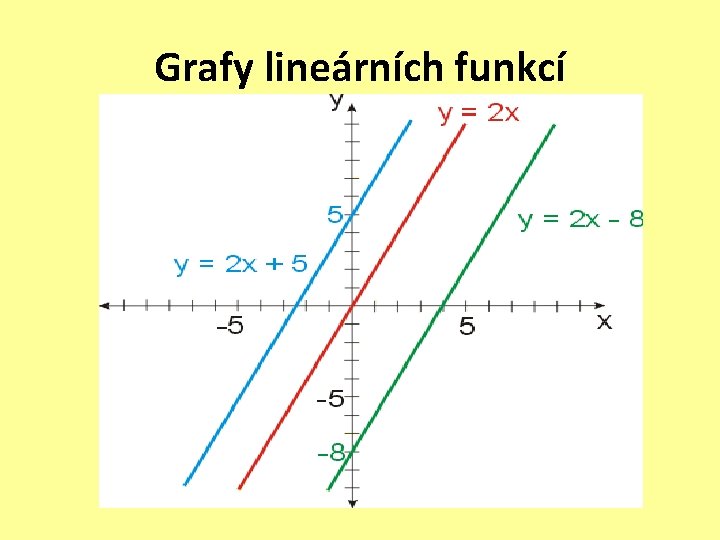
Grafy lineárních funkcí

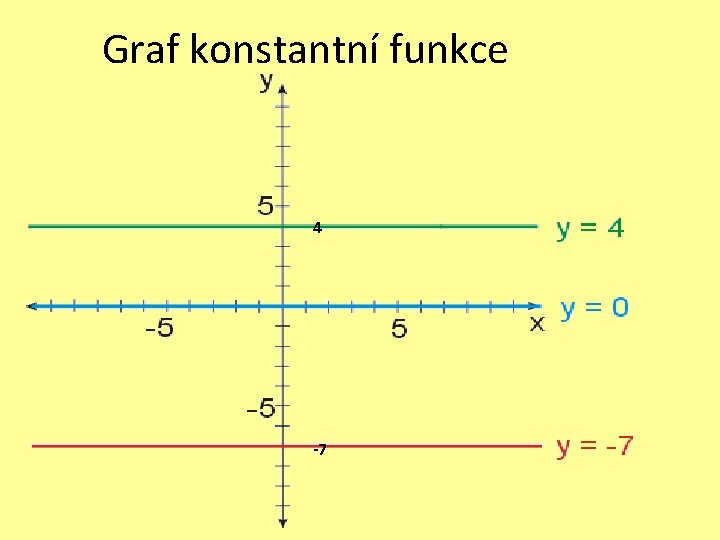
Konstantní funkce je taková funkce, jejíž hodnota se pro žádné x nemění. y = q nebo y = b k = 0 a = 0 q = libovolné b = libovolné Grafem konstantní funkce je přímka rovnoběžná s osou x. (např: y = 4; y = 0; y = -7)

Graf konstantní funkce 4 -7

Přímá úměrnost je zvláštním případem lineární funkce , která má q = 0 nebo b = 0

Rovnice přímé úměrnosti y = a. x y = k. x Číslu k říkáme směrnice Pokud je k kladné, funkce roste Pokud je k záporné, funkce klesá

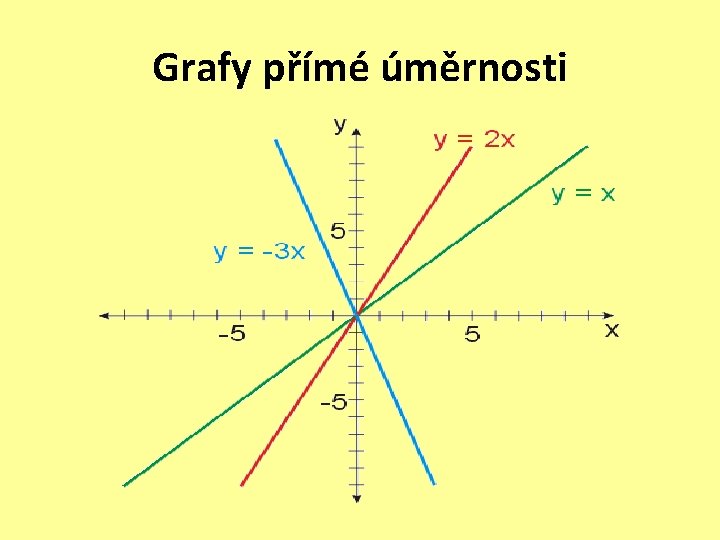
Grafem přímé úměrnosti je vždy přímka , která prochází vždy počátkem soustavy souřadnic

Grafy přímé úměrnosti

Ostatní lineární funkce vznikají v podstatě posunutím přímé úměrnosti. Číslu q tedy říkáme posunutí. Posunutí určuje, v jakém bodě protne graf osu y

Příklady Je dána funkce f: y=2 x-1 ; x R. Rozhodněte, která z následujících dvojic [x; y] patří funkci f. [0; 1] [0; -1] [3/2; -2] [0, 25; -1/2] [-1/4; -1, 5]

Příklady Je dána funkce f: y=2 x-1 ; x R. Rozhodněte, která z následujících dvojic [x; y] patří funkci f. [0; 1] [0; -1] [3/2; -2] [0, 25; -1/2] [-1/4; -1, 5]

Shrnutí Speciálním případem lineární funkce, jejíž graf prochází počátkem souřadnic se nazývá přímá úměrnost. Grafy lineárních funkcí jsou vždy přímky. U konstantních funkcí jsou přímky rovnoběžné s osou x

• Zdroje : vlastní • skripta UP Olomouc 1980