Linear Prediction Coding LPC History Originally developed to

Linear Prediction Coding (LPC) • History: Originally developed to compress (code) speech • Broader Implications – – Models the harmonic resonances of the vocal tract Provide features useful for speech recognition Part of speech synthesis algorithms IIR Filter, to eliminate noise from a signal • Concept – Predict samples with linear combinations of previous values to create a LPC signal – The residue or error is the difference between the signal and the prediction

LPC Calculations • Predict the values of the next sample Ŝ[n] = ∑ k=1, P ak s[n−k] – P is the LPC order – Accurate vocal tract model: P = sample rate*1000 + 2 – The LPC algorithm computes the ak coefficients • The error signal (e[n]) is called the LPC residual e[n]=s[n]− ŝ[n] = s[n]− ∑ k=1, p ak s[n−k] • Goal: find ak coefficients that minimize the LPC residual

Linear Predictive Compression (LPC) Concept • For a frame of the signal, find the optimal coefficients, predicting the next values using sets of previous values • Instead of outputting the actual data, output the residual, plus the coefficients • Less bits are needed, which results in compression Pseudo Code WHILE not EOF READ frame of signal x = prediction(frame) error = x – s[n] WRITE LPC coefficients WRITE error

Linear Algebra Background • N linear independent equations; P unknowns • If N<P, ∞ number of potential solutions x + y = 5 // one equation, two unknowns Solutions are along the line y = 5 -x • If N=P, there is at most one unique solution x + y = 5 and x – y = 3, solution x=4, y=1 • If N>P, there are no solutions No solutions for: x+y = 4, x – y = 3, 2 x + 7 = 7 The best we can do is find the closes fit

Least Squares: minimize error • First Approach: Linear algebra – find orthogonal projections of vectors onto the best fit • Second Approach: Calculus – Use derivative with zero slope to find best fit

Solving n equations and n unknowns Numerical Algorithms • Gaussian Elimination – Complexity: O(n 3) • Successive Iteration – Complexity varies • Cholskey Decomposition – More efficient, still O(n 3) • Levenson-Durbin – Complexity: O(n 2) – Symmetric Toeplitz matrices Definitions for any matrix, A Transpose (AT): Replace all aij by aji Symmetric: AT = A Toeplitz: Descending diagonals to the right have equal values Lower/Upper triangular: No non zero values above/below diagonal

Symmetric Toeplitz Matrices Example • Flipping rows and columns produces the same matrix • Every diagonal to the right contains the same value

Levinson Durbin Algorithm or Step 0 E 0 = 1 [r 0 Initial Value] Step 1 E 1 = -3 [ (1 -k 12)E 0] k 1 = 2 [r 1/E 0] Step 2 E 2 = -8/3 [ (1 -k 22)E 1] k 2 = 1/3 [(r 2 – a 11 r 1)/E 1] Step 3 E 3 = -5/2 [(1 -k 32)E 2 k 3 = 1/4 [(r 3 – a 21 r 2 – a 22 r 1)/E 2] Step 4 E 4 = -12/5 [(1 -k 42) E 3] k 4 = 1/5 [r 4 – a 31 r 3 – a 32 r 2 – a 33 r 1)/E 3] a 11=2 [k 1] a 21=4/3 [a 11 -k 2 a 11] a 22=1/3[k 2] a 31=5/4 [a 21 -k 3 a 22] a 32=0 [a 22 -k 3 a 21] a 33=1/4 [k 3] a 41=6/5 [a 31 -k 4 a 33] a 42=0 [a 32 -k 4 a 32] a 43=0[a 33 -k 4 a 31] a 44=1/5[k 4] Verify results by plugging a 41, a 42, a 43, a 44 back into the equations 6/5(1) + 0(2) + (0)3 + 1/5(4) = 2, 6/5(2) + 0(1) + 0(2) + 1/5(3) = 3 6/5(3) + 0(2) + 0(1) + 1/5(2) = 4, 6/5(4) + 0(3) + 0(2) + 1/5(1) = 5

Levinson-Durbin Pseudo Code E 0 = r 0 FOR step = 1 TO P kstep = ri FOR i = 1 TO step-1 THEN kstep -= ai-1, i * rstep-i kstep /= Estep-1 Estep = (1 – k 2 step)Estep-1 astep, step = kstep-1 For i = 1 TO step-1 THEN astep, i = astep-1, I – kstep*astep-1, step-i Note: ri are the row 1 matrix coefficients

Cholesky Decomposition • Requirements: – Symmetric (same matrix if flip rows and columns) – Positive definite matrix Matrix A is real positive definite if and only if for all x ≠ 0, x. TAx > 0 • Solution – Factor matrix A into: A = LLT where L is lower triangular – Perform forward substitution to solve: L(LT[ak]) = [bk] – Use the resulting vector, [xi], in the above step to perform a backward substitution to solve for LT[ak] = [xi] • Complexity – Factoring step: O(n 3/3) – Forward and Backward substitution: O(n 2)

Cholesky Factorization Result:

Cholesky Factorization Pseudo Code FOR k=1 TO n-1 lkk = a½kk FOR j = k+1 TO n ljk = ajk/ lkk FOR j = k+1 TO n FOR i = j TO n aij = aij – lik ljk lnn = ann • • Column index: k Row index: j Elements of matrix A: aij Elements of matrix L: l

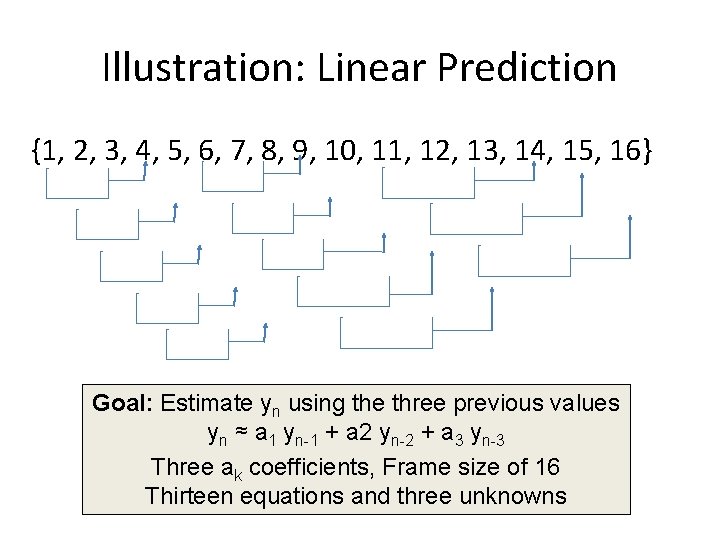
Illustration: Linear Prediction {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16} Goal: Estimate yn using the three previous values yn ≈ a 1 yn-1 + a 2 yn-2 + a 3 yn-3 Three ak coefficients, Frame size of 16 Thirteen equations and three unknowns

LPC Basics • Predict x[n] from x[n-1], … , x[n-P] – en = yn - ∑k=1, P ak yn-k – en is the error between the projection and the actual value – The goal is to find the coefficients that produce the smallest en value • Concept – – – Square the error Take the partial derivative with respect to each ak Optimize (The minimum slope has a derivative of zero) Result: P equations and P unknowns Solve using either the Cholesky or Levinson-Durbin algorithms

LPC Derivation • One linear prediction equation: en = yn - ∑k=1, P ak yn-k Over a whole frame we have n equations and k unknowns • Sum en over the entire frame: E = ∑n=0, N-1(yn - ∑k=1, P ak yn-k) • Square the total error: E 2 = ∑n=0, N-1 (yn - ∑k=1, P ak yn-k)2 • Partial derivative with respect to each aj; generates P equations (Ej) Like a regular derivative treating only aj as a variable 2 Ej = 2(∑n=0, N-1 (yn - ∑k=1, P akyn-k)yn-j) Calculus Chain Rule: if y = y(u(x)) then dy/dx = dy/du * du/dx • Set each Ej to zero (zero derivative) to find the minimum P errors for j = 1 to P then 0 = ∑n=0, N-1 (yn - ∑k=1, P akyn-k)yn-j (j indicates the equation) • Rearrange terms: for each j of the P equations, ∑n=0, N-1 ynyn-j = ∑n=0, N-1∑k=1, Pakyn-j = ∑k=1, P∑n=1, Nakyn-j • Yule Walker equations: IF φ(j, 0)= ∑n=0, N-1 ynyn-j, THEN φ(j, 0) = ∑k=1, Pakφ(j, k) • Result: P equations and P unknowns (ak), one solution for the best prediction

LPC: the Covariance Method • Result from previous: φ(j, k) = ∑k=1, P∑n=0, N-1 yn-kyn-j • Equation j: φ(j, 0)=∑k=1, Pakφ(j, k) • • Now we have P equations and P unknowns Because φ(j, k) = φ(k, j), the matrix is symmetric Solution requires O(n 3) iterations (ex: Cholskey’s decomposition) Why covariance? It’s not probabilistic, but the matrix looks similar

Covariance Example Recall: φ(j, k) = ∑n=start, start+N-1 yn-kyn-j Where equation j is: φ(j, 0) = ∑k=1, Pakφ(j, k) • • • • Signal: { … , 3, 2, -1, -3, -5, -2, 0, 1, 2, 4, 3, 1, 0, -1, -2, -4, -1, 0, 3, 1, 0, … } Frame: {-5, -2, 0, 1, 2, 4, 3, 1}, Number of coefficients: 3 φ(1, 1) = -3*-3 +-5*-5 + -2*-2 + 0*0 + 1*1 + 2*2 + 4*4 + 3*3 = 68 φ(2, 1) = -1*-3 +-3*-5 + -5*-2 + -2*0 + 0*1 + 1*2 + 2*4 + 4*3 = 50 φ(3, 1) = 2*-3 +-1*-5 + -3*-2 + -5*0 + -2*1 + 0*2 + 1*4 + 2*3 = 13 φ(1, 2) = -3*-1 +-5*-3 + -2*-5 + 0*-2 + 1*0 + 2*1 + 4*2 + 3*4 = 50 φ(2, 2) = -1*-1 +-3*-3 + -5*-5 + -2*-2 + 0*0 + 1*1 + 2*2 + 4*4 = 60 φ(3, 2) = 2*-1 +-1*-3 + -3*-5 + -5*-2 + -2*0 + 0*1 + 1*2 + 2*4 = 36 φ(1, 3) = -3*2 +-5*-1 + -2*-3 + 0*-5 + 1*-2 + 2*0 + 4*1 + 3*2 = 13 φ(2, 3) = -1*2 +-3*-1 + -5*-3 + -2*-5 + 0*-2 + 1*0 + 2*1 + 4*2 = 36 φ(3, 3) = 2*2 +-1*-1 + -3*-3 + -5*-5 + -2*-2 + 0*0 + 1*1 + 2*2 = 48 φ(1, 0) = -3*-5 +-5*-2 + -2*0 + 0*1 + 1*2 + 2*4 + 4*3 + 3*1 = 50 φ(2, 0) = -1*-5 +-3*-2 + -5*0 + -2*1 + 0*2 + 1*4 + 2*3 + 4*1 = 23 φ(3, 0) = 2*-5 +-1*-2 + -3*0 + -5*1 + -2*2 + 0*4 + 1*3 + 2*1 = -12

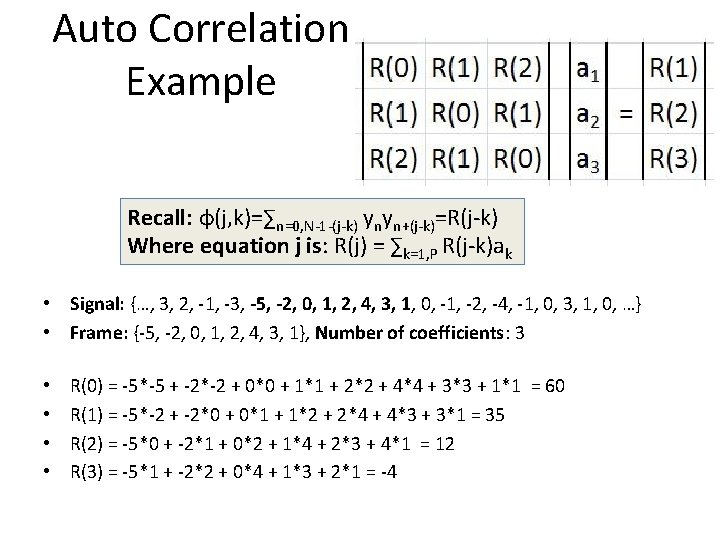
Auto-Correlation Method • • Assume: all signal values outside of the frame (0<j<N-1) assumed zero Correlate from -∞ to ∞ (most values are 0) The LPC formula for φ becomes: φ(j, k)=∑n=0, N-1 -(j-k) ynyn+(j-k)=R(j-k) The Matrix is now in the Toplitz format – The Levinson Durbin algorithm applies – Implementation complexity: O(n 2)

Auto Correlation Example Recall: φ(j, k)=∑n=0, N-1 -(j-k) ynyn+(j-k)=R(j-k) Where equation j is: R(j) = ∑k=1, P R(j-k)ak • Signal: {…, 3, 2, -1, -3, -5, -2, 0, 1, 2, 4, 3, 1, 0, -1, -2, -4, -1, 0, 3, 1, 0, …} • Frame: {-5, -2, 0, 1, 2, 4, 3, 1}, Number of coefficients: 3 • • R(0) = -5*-5 + -2*-2 + 0*0 + 1*1 + 2*2 + 4*4 + 3*3 + 1*1 = 60 R(1) = -5*-2 + -2*0 + 0*1 + 1*2 + 2*4 + 4*3 + 3*1 = 35 R(2) = -5*0 + -2*1 + 0*2 + 1*4 + 2*3 + 4*1 = 12 R(3) = -5*1 + -2*2 + 0*4 + 1*3 + 2*1 = -4

LPC Transfer Function • Predict the values of the next sample Ŝ[n] = ∑ k=1, p ak s[n−k] • The error signal (e[n]), is the LPC residual e[n]=s[n]− ŝ[n] = s[n]− ∑ k=1, p ak s[n−k] • Perform a Z-transform of both sides E(z)=S(z)− ∑k=1, pak S(z)z−k • Factor S(z) E(z) = S(z)[ 1−∑k=1, p ak z−k ]=S(z)A(z) • Compute the transfer function: S(z) = E(z)/A(z) • Conclusion: LPC is an all pole IIR filter

Speech and the LPC model • LPC all-pole IR filter: yn = Gxn - ∑k=1, N ak yn – The residual models the glottal source – The summation approximates the vocal tract harmonics • Challenges (Problems in synthesis) – The residual does not accurately model the source (glottis) – The filter does not model radiation from the lips – The filter does not account for nasal resonances • Possible solutions – Additional poles can somewhat increase the accuracy • 1 pole pair for each 1 k of sampling rate • 2 more pairs can better estimate the source and lips – Introduce zeroes into the model – More robust analysis of the glottal source and lip radiation

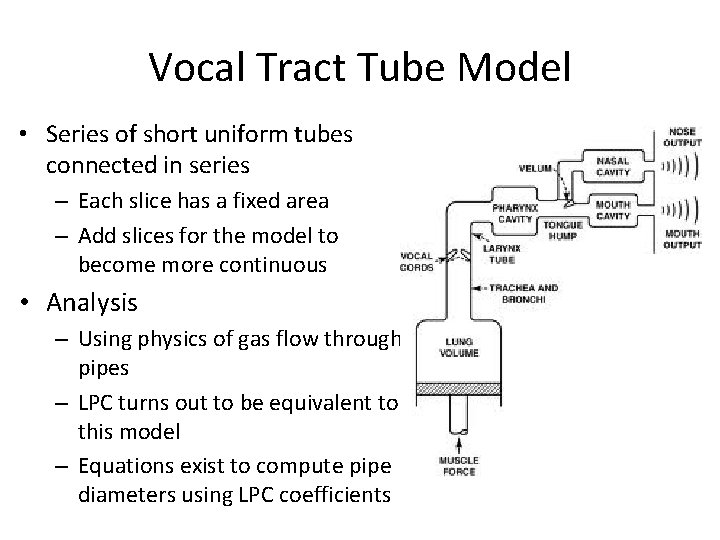
Vocal Tract Tube Model • Series of short uniform tubes connected in series – Each slice has a fixed area – Add slices for the model to become more continuous • Analysis – Using physics of gas flow through pipes – LPC turns out to be equivalent to this model – Equations exist to compute pipe diameters using LPC coefficients

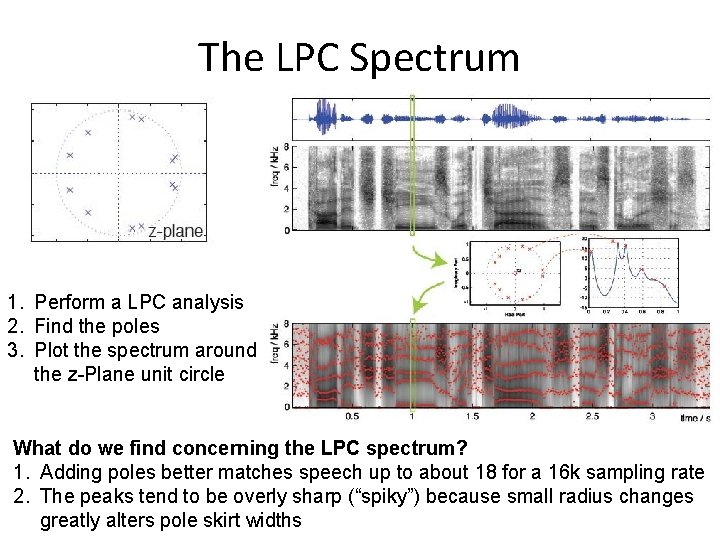
The LPC Spectrum 1. Perform a LPC analysis 2. Find the poles 3. Plot the spectrum around the z-Plane unit circle What do we find concerning the LPC spectrum? 1. Adding poles better matches speech up to about 18 for a 16 k sampling rate 2. The peaks tend to be overly sharp (“spiky”) because small radius changes greatly alters pole skirt widths