LIMITE Limita zaporedja tevilo L je limita zaporedja







![Pomožni rezultat: Če se dolžine intervalov [a 1, b 1] ⊇ [a 2, b Pomožni rezultat: Če se dolžine intervalov [a 1, b 1] ⊇ [a 2, b](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-9.jpg)
![Lastnosti zveznih funkcij f: [a, b] → ℝ zvezna f je omejena [a, b] Lastnosti zveznih funkcij f: [a, b] → ℝ zvezna f je omejena [a, b]](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-10.jpg)
![f: [a, b] → ℝ zvezna f zavzame maksimum in minimum Ker je zaloga f: [a, b] → ℝ zvezna f zavzame maksimum in minimum Ker je zaloga](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-11.jpg)
![f: [a, b] ℝ zvezna f zavzame vse vrednosti med min f in max f: [a, b] ℝ zvezna f zavzame vse vrednosti med min f in max](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-12.jpg)















- Slides: 37

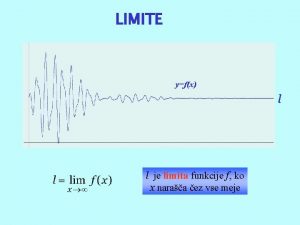
LIMITE Limita zaporedja Število L je limita zaporedja (xn), če so števila xn blizu L za vse dovolj velike n. Bolj natančno, L je limita zaporedja (xn) če velja naslednje: za vsako pozitivno število ε obstaja tako naravno število N, da je |xn-L|<ε , za vse n, ki so večji od N. Pišemo. Limita funkcije Število L je limita funkcije f pri točki a če velja naslednje: za vsako pozitivno število ε obstaja interval I okoli točke a, da je | f(x)-L|<ε pri vseh x iz I. Pišemo.

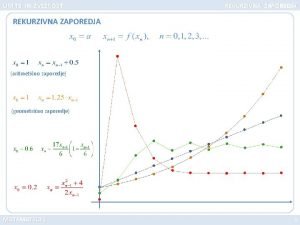
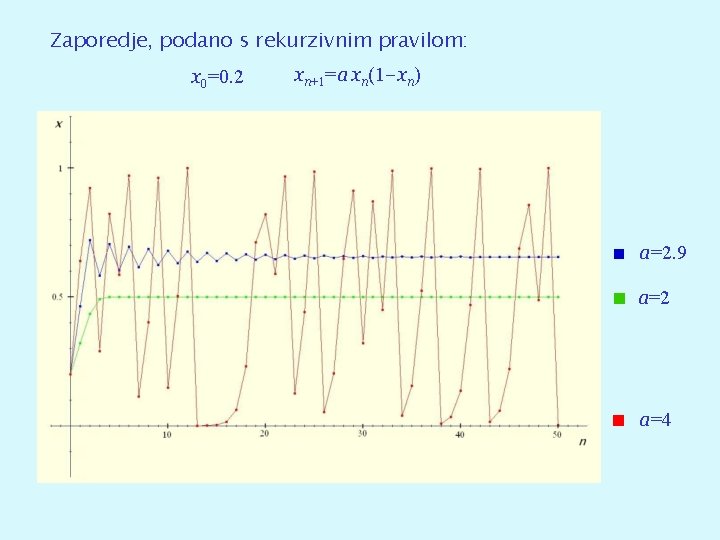
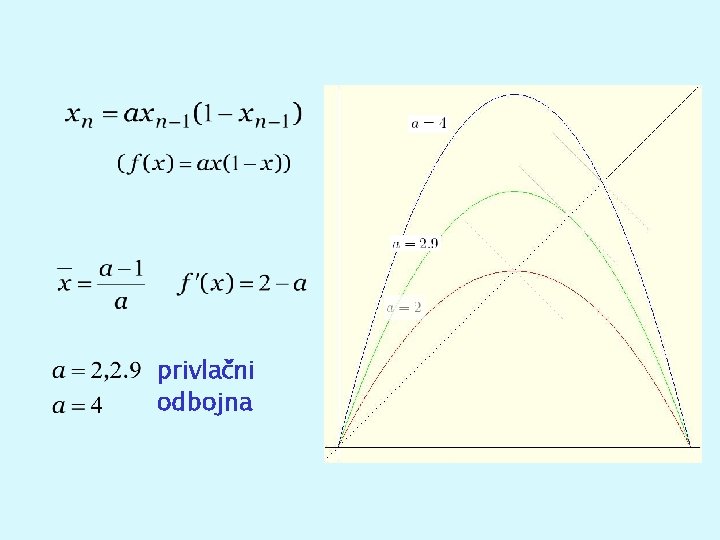
Zaporedje, podano s rekurzivnim pravilom: x 0=0. 2 xn+1=a xn(1 -xn) a=2. 9 a=2 a=4

Poskakujoča žoga višina žoge hitrost pospešek t Višina se spreminja zvezno, hitrost pa nezvezno. Pospešek se prav tako spreminja nezvezno, vendar ga lahko dopolnimo do zvezne funkcije.

Zaporedje (xn) je naraščajoče, če je xn≤xn+1. Če je (xn) navzgor omejeno, ima natančno zgornjo mejo L. Pokažimo, da je § Za pozitiven ε je L-ε manjše od L. § Zaradi lastnosti natančne zgornje meje obstaja tak N, da je x. N>L-ε. § (xn) je naraščajoče, zato za vsak n ≥ N velja L-ε < xn ≤ L, torej je |L-xn|<ε. Vsako naraščajoče, navzgor omejeno zaporedje ima limito.

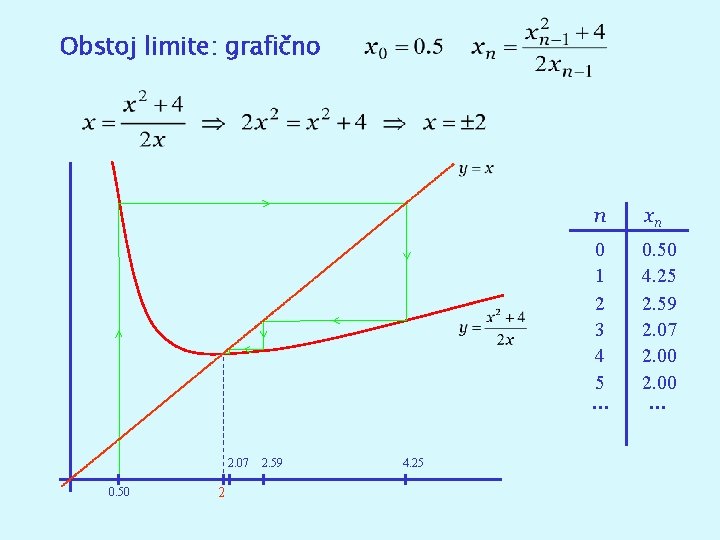
Primer x 0=0. 2 xn+1=2 xn(1 -xn) xn+1 -xn = 2 xn(1 -xn)-xn = xn(1 -2 xn) Če je 0 ≤ xn ≤ 0. 5, je xn ≤ xn+1. Povrhu, če je 0 ≤ xn ≤ 0. 5, je xn+1 = 2 xn(1 -xn) ≤ 0. 5 0 1 y =2 x (1 -x) Zaporedje je naraščajoče in omejeno, torej ima limito.

Računska pravila za limite (za zaporedja in za funkcije) (če je L 2≠ 0) Pravila smemo uporabiti le kadar limite obstajajo!

Zvezne funkcije Funkcija f je zvezna pri točki a, če je f definirana v a in je Funkcija f je zvezna, če je zvezna pri vseh točkah kjer je definirana. Primeri: vse elementarne funkcije, večina funkcij, ki nastopajo pri modeliranju naravnih procesov. Alternativna definicija: Funkcija f je zvezna pri točki a, če je v tej točki definirana in če za vsak pozitiven ε obstaja tak interval I okoli točke a, da je |f(a)-f(x)|<ε za vse x∈I. Intuitivno: funkcija je zvezna pri a, če so blizu a njene vrednosti blizu f(a). Funkcija n spremenljivk je zvezna pri neki točki v ℝn če se njena limita pri tej točki ujema s funkcijsko vrednostjo.

Zveznost elementarnih funkcij f, g: A → B zvezni funkciji f+g je zvezna. Podobno sklepamo za ostale računske operacije. f: A → B, g: B → C zvezni funkciji gof je zvezna. Vse osnovne funkcije so zvezne, računske operacije in sestavljanje funkcij pa ohranjajo zveznost. Vse elementarne funkcije so zvezne.
![Pomožni rezultat Če se dolžine intervalov a 1 b 1 a 2 b Pomožni rezultat: Če se dolžine intervalov [a 1, b 1] ⊇ [a 2, b](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-9.jpg)
Pomožni rezultat: Če se dolžine intervalov [a 1, b 1] ⊇ [a 2, b 2] ⊇ [a 3, b 3] ⊇. . . manjšajo proti 0 (tj. lim(bn-an)=0), potem je v njihovem preseku natanko ena točka a 1 a 2 a 3 b 2 b 1 Leva krajišča intervalov so naraščajoče omejeno zaporedje, zato imajo limito A. Desna krajišča so padajoče omejeno zaporedje in imajo limito B. Presek vseh intervalov je ravno interval [A, B]. Če bi imeli A<B, bi v zaporedju obstajal interval krajši od B-A. Zato je A=B in v preseku je ena točka.
![Lastnosti zveznih funkcij f a b ℝ zvezna f je omejena a b Lastnosti zveznih funkcij f: [a, b] → ℝ zvezna f je omejena [a, b]](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-10.jpg)
Lastnosti zveznih funkcij f: [a, b] → ℝ zvezna f je omejena [a, b] razpolovimo. Če bi bila f neomejena, bi morala biti neomejena vsaj na eni od polovic. To polovico razpolovimo naprej in sklepamo enako: vsaj na enem delu je f neomejena. Z nadaljevanjem postopka dobimo padajoče zaporedje intervalov na katerih je f neomejena in je vsak polovica prejšnjega. Naj bo p točka, ki je presek teh intervalov. Po konstrukciji je f neomejena na vsakem intervalu, ki vsebuje p. To je v nasprotju s privzetkom, da je f zvezna pri p, saj bi na nekem intervalu okoli p moralo veljati |f(p)-f(x)|<1. Protislovje je povzročil privzetek, da je f neomejena, zato sklepamo, da je f omejena.
![f a b ℝ zvezna f zavzame maksimum in minimum Ker je zaloga f: [a, b] → ℝ zvezna f zavzame maksimum in minimum Ker je zaloga](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-11.jpg)
f: [a, b] → ℝ zvezna f zavzame maksimum in minimum Ker je zaloga vrednosti funkcije f omejena, ima natančno zgornjo mejo M. Če M ne bi bila dosežena v nobeni točki domene [a, b] potem bi predpis g(x)=1/(M-f(x)) podal zvezno neomejeno funkcijo g: [a, b] → ℝ. To ni mogoče, zato sklepamo, da je f(x)=M za nek x∈[a, b], torej f zavzame maksimum M na [a, b]. Podobno sklepamo, da f zavzame tudi minimum na intervalu [a, b].
![f a b ℝ zvezna f zavzame vse vrednosti med min f in max f: [a, b] ℝ zvezna f zavzame vse vrednosti med min f in max](https://slidetodoc.com/presentation_image_h/0631572094d94aaa02b73c0b910e2096/image-12.jpg)
f: [a, b] ℝ zvezna f zavzame vse vrednosti med min f in max f Privzemimo f(a)<f(b) in izberimo neko vmesno vrednost v: f(a)<v<f(b) v f(a) c a b Množica vseh x ∈ [a, b] za katere velja f(x) < v je neprazna in omejena, zato ima natančno zgornjo mejo, ki jo označimo s c. Trdimo f(c)=v. Res, f(c) ne more biti večji od v, saj so poljubno blizu c točke v katerih so vrednosti f manjše od v. Po drugi strani pa f(c) ne more biti niti manjši od v, saj so v vseh točkah intervala, ki so desno od c vrednosti f večje od v. Ostane le še možnost f(c)=v.

Zvezna funkcija na zaprtem intervalu zavzame minimum, maksimum in vse vmesne vrednosti. Njena zaloga vrednosti je zaprti interval [min f, max f ].

Bisekcija - določanje ničel zveznih funkcij 3 4. 67 5. 25 4. 80 4. 76 4. 85 4. 5 Ničla je ≈ 4. 78 6


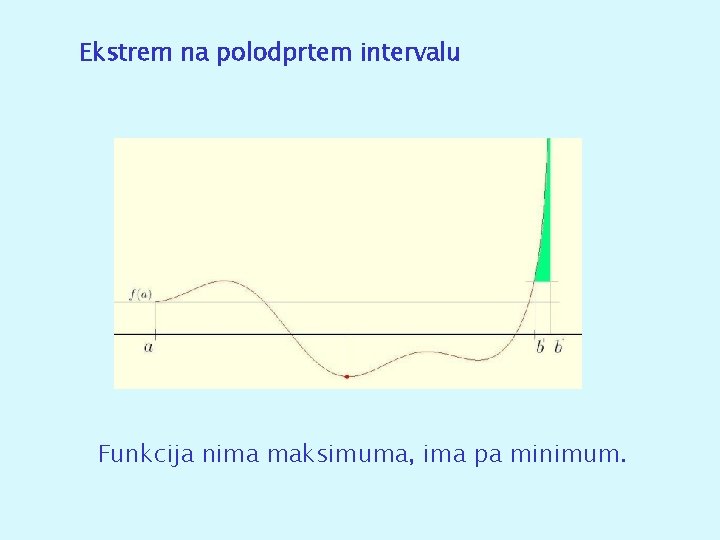
Ekstrem na polodprtem intervalu Funkcija nima maksimuma, ima pa minimum.

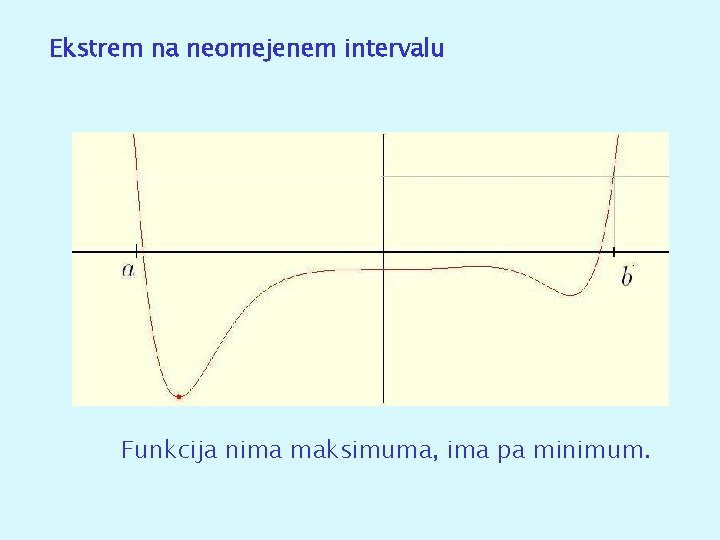
Ekstrem na neomejenem intervalu Funkcija nima maksimuma, ima pa minimum.

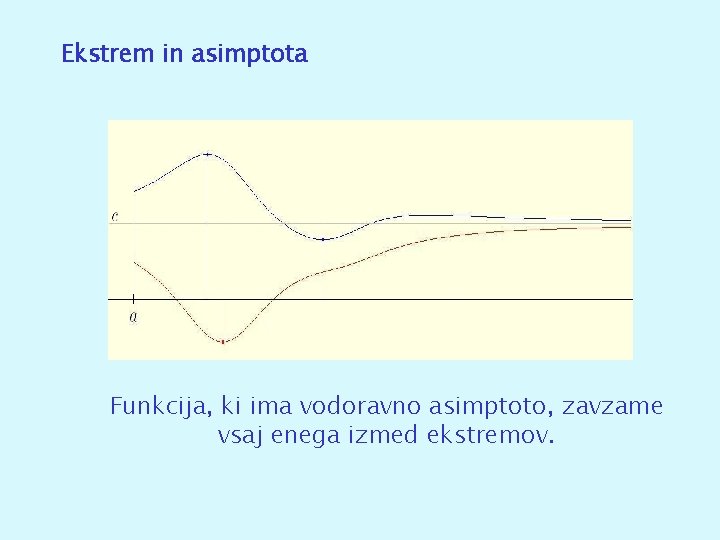
Ekstrem in asimptota Funkcija, ki ima vodoravno asimptoto, zavzame vsaj enega izmed ekstremov.

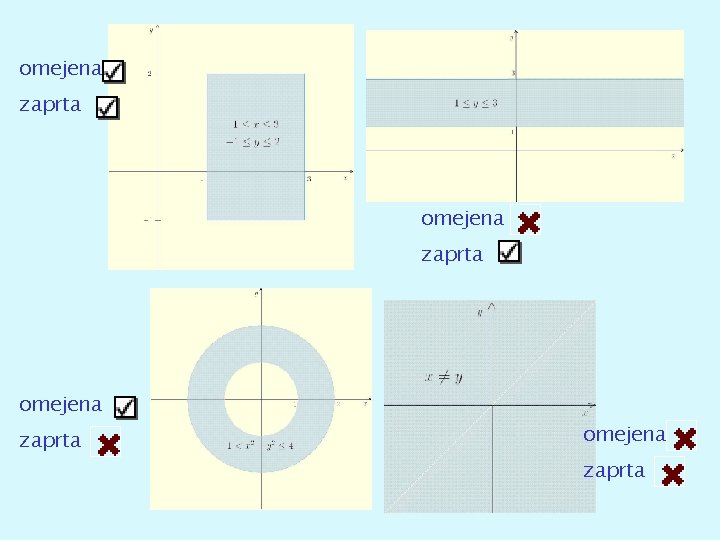
Ekstremi funkcij več spremenljivk A⊆ℝ n je omejena, če so vse točke oddaljene od izhodišča za manj kot neko število M; je zaprta, če vsebuje vse točke, ki so na njenem robu; Točka a je na robu A če so v njeni bližini tako točke, ki so v A, kot točke, ki niso v A.

omejena zaprta

Zvezna funkcija na omejeni in zaprti množici zavzame maksimum in minimum. Če je množica povezana, potem funkcija zavzame tudi vse vmesne vrednosti. (Množica je povezana, če lahko poljubni dve točki povežemo s krivuljo, ki leži v celoti znotraj množice. )

Ekstrem funkcije več spremenljivk na neomejeni množici: Naj bo f: ℝ 2→ℝ zvezna in naj velja Funkcija zavzame minimum.

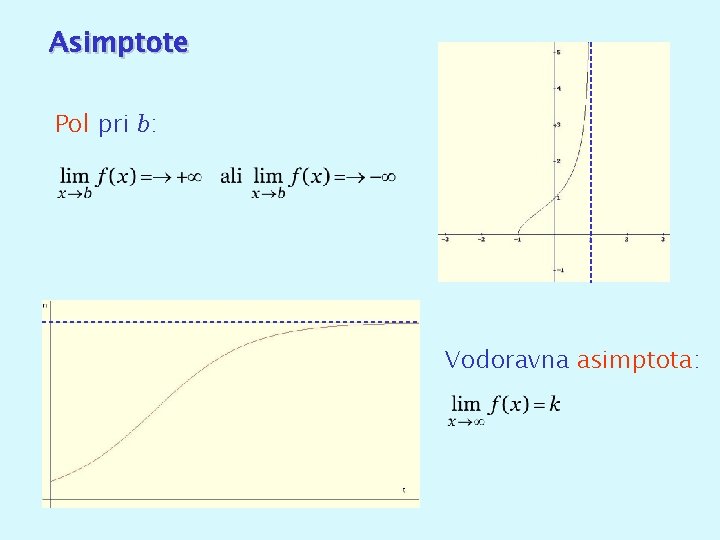
Asimptote Pol pri b: Vodoravna asimptota:

Poševna asimptota Primer

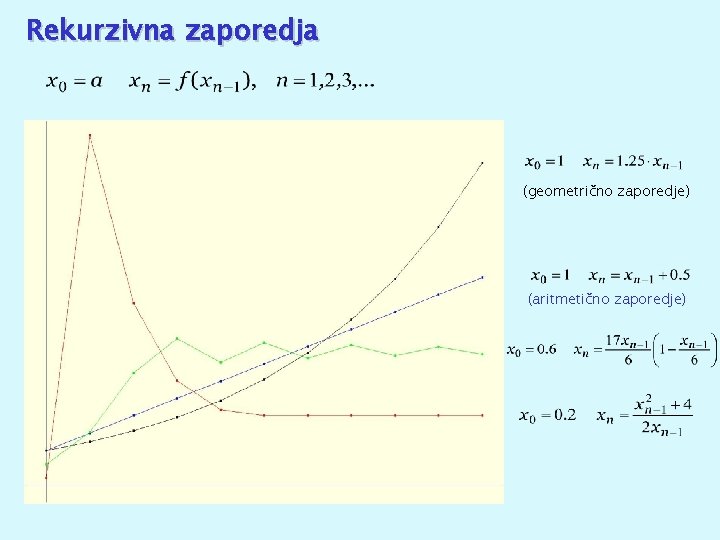
Rekurzivna zaporedja (geometrično zaporedje) (aritmetično zaporedje)

Naj bo f zvezna. Če obstaja potem za x velja: Edine možne limite so rešitve enačbe f(x)=x. negibne točke

Obstoj limite: grafično 2. 07 0. 50 2 2. 59 4. 25 n xn 0 1 2 3 4 5 … 0. 50 4. 25 2. 59 2. 07 2. 00 …

Obstoj limite: analitično Funkcija f je skrčitev na intervalu I, če za k<1 velja Privzemimo, da je f skrčitev na intervalu I okoli negibne točke Pravimo, da je negibna točka funkcije f privlačna (atraktor). Rekurzivno zaporedje, ki se približa , konvergira proti je privlačna negibna točka. .

privlačni odbojna


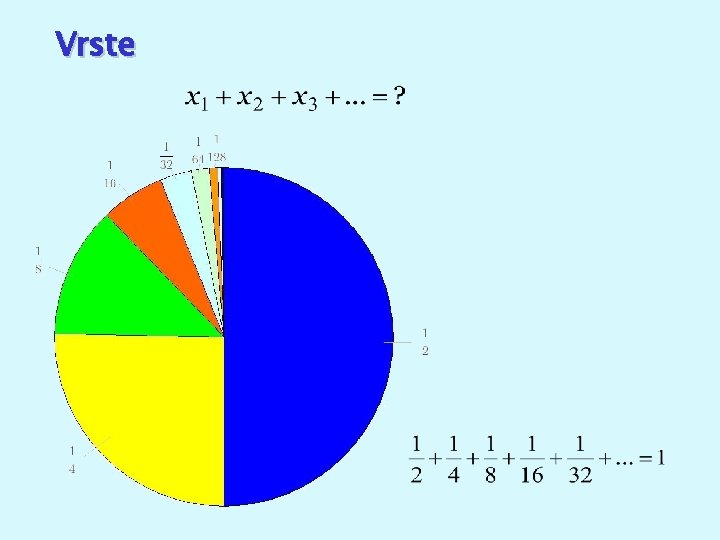
Vrste

zaporedje delnih vsot Vsota vrste je, po definiciji, enaka limiti zaporedja delnih vsot.

Primeri (geometrijska vrsta)

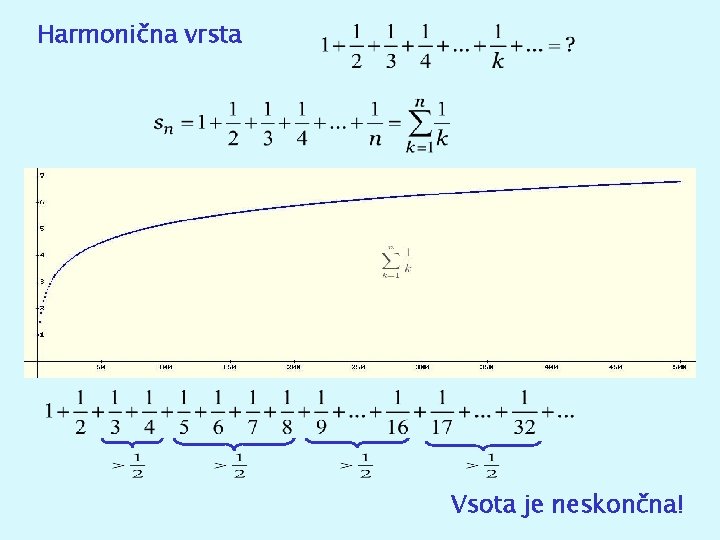
Harmonična vrsta Vsota je neskončna!

Vrste s pozitivnimi členi: xn ≥ 0 Zaporedje delnih vsot je naraščajoče. Limito ima, ko je navzgor omejeno. Primerjalni kriteriji za konvergenco vrst I. II. (Vrsti sta primerljivi. )

Geometrijska vrsta: Harmonična vrsta: Vrsto lahko seštejemo, če splošni člen dovolj hitro konvergira proti 0. Hitrost konvergence ocenimo tako, da poiščemo primerljivo geometrijsko ali harmonično vrsto. Primer vsota obstaja

Splošne vrste: Alternirajoče vrste:
 Limita zaporedja
Limita zaporedja Limita zaporedja
Limita zaporedja Rekurzivna zaporedja
Rekurzivna zaporedja Konvergentno in divergentno zaporedje
Konvergentno in divergentno zaporedje Una spezzata intrecciata aperta di 6 lati
Una spezzata intrecciata aperta di 6 lati Con que limita europa
Con que limita europa Linea spezzata aperta intrecciata
Linea spezzata aperta intrecciata Zona appenninica italia
Zona appenninica italia Teorema do limite central macs
Teorema do limite central macs Quando chegamos no limite
Quando chegamos no limite Limite nord sud
Limite nord sud Osteocondroma
Osteocondroma Estereocilios
Estereocilios Límite
Límite Euler limite
Euler limite Diferencial
Diferencial Rango de ci
Rango de ci Napiers bone
Napiers bone Limites laterais
Limites laterais Limite divergente
Limite divergente Teorema central del limite
Teorema central del limite Camada limite termica
Camada limite termica Litizzazione significato
Litizzazione significato Ley límite de debye-hückel
Ley límite de debye-hückel Teorema do limite central
Teorema do limite central 1590 microscopio
1590 microscopio Velocità limite di caduta
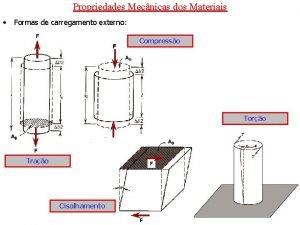
Velocità limite di caduta Limite de escoamento
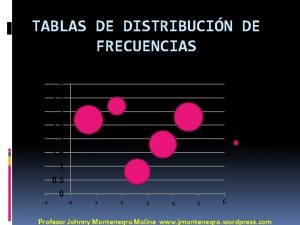
Limite de escoamento Grafico bivariado de graficas apiladas
Grafico bivariado de graficas apiladas Placa de filipinas
Placa de filipinas Coefficient rhéologique du sol
Coefficient rhéologique du sol Sigma ammissibile
Sigma ammissibile Modulo young aço
Modulo young aço Limites
Limites Teorema de limite central
Teorema de limite central Variao
Variao Ipotesi nulla
Ipotesi nulla Gaz idealny
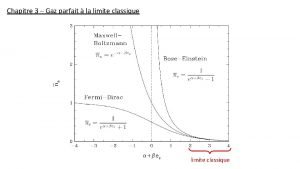
Gaz idealny